Playing within Kelly [VP]

How do you figure out if a certain play is within full Kelly?

You would use Kelly and the formula (edge/variance * bankroll) for VP if you were playing something like FPDW, or a game with an edge "off the top" (100%+ return games). I understand that stuff.

What I don't understand is something like the following situation: Let's say you find a promotion where you have to do $10,000 coin in and you get back $200 in cash. You only get the cash if you complete the entire $10K coin in requirement. You find 9/6 JOB for $1 denom with 5 lines. Your edge is 1.54%. You can figure out the standard deviation using that formula (found here: https://wizardofodds.com/games/video-poker/appendix/3/ ) for the entire $10K coin in play. Once you start the play, you can't decide to quit (you get no +EV for quitting before $10K coin in). So before starting the play, you have to determine if your bankroll is large enough for this.

This is NOT the same as the following: You have a $1 9/6 JOB with 5 lines, 0.1% cash back, and have a 20x point multiplier day (1.54% edge). Here, you can determine what your optimal bet is, and if your optimal bet is $25 or more, then you are within Kelly to make the play. If, during the play, you start to lose, and your bankroll is no longer sufficient to play the game, you simply quit.


The first case, you cannot quit and must play the required amount. In the second case, you can quit whenever you want. I understand how to do the calculations for the second example (edge/variance * bankroll). But I do not understand how to do the calculation (or if it's different or what) for the first example.


I know how to calculate the standard deviation for $10K coin in on $1 9/6 JOB (using link above). The standard deviation for that play is about $1,169.

I don't think the Kelly Criterion works well for VP. The distribution is so skewed by the Royal Flush that it takes millions of hands for your results to converge to normal, so measures like variance don't really mean as much. To determine if it's a play or not I usually run a simulation; look at the worst-case scenario and determine if my bankroll can sustain such a hit.

JOB might be a special case. The smaller pays converge pretty quickly which only leaves the royal, so you end up with a bimodal distribution. Sessions where you hit a royal and sessions where you didn't. Without the royal you'll be playing at about a 2.5% house edge, so you'll most likely lose at this promotion but if you do hit a royal you'll be almost $4K ahead. You can estimate the chance of hitting the royal by using the exponential distribution Probability= 1-exp(-1*hands played/cycle length)

Here's how I calculated Kelly in my A-Z blackjack thread. You apply the same math but change your win% and loss% to match your 'advantage' in whatever game you're playing. Also, of course, apply your own bankroll as Kelly bet sizes for your bankroll. This might not be exactly tailored to your question, but I hope it points you in the right direction to help answer it!



Note: Don't ever go above double kelly, the fluctuations in variance are proven to crush just about any bankroll and inevitably hit bust.

Quote: Tortoise

To determine if it's a play or not I usually run a simulation; look at the worst-case scenario and determine if my bankroll can sustain such a hit.
)

I thinks that's a good way for some.
Normally I would just go by experience.

But when I first started playing and wanted a better Idea. My only program had a super fast auto play, It didn't even show high or low points, I would start different sessions and check throughout the day and to see how bad you could possibly run.

Expected loss is a bunch of BS. Well I mean that if you play perfect and hit every hand you are supposed to in your coin in, sure that's what you will lose. My rough guess is that for a $10k coin in on dollars you should take about $2000 with you, half a royal. Of course you can adjust based on the variance of the game. Less on JoB, more on DDB. DW and DB somewhere in between.

Quote: Tortoise

I don't think the Kelly Criterion works well for VP. The distribution is so skewed by the Royal Flush that it takes millions of hands for your results to converge to normal, so measures like variance don't really mean as much. To determine if it's a play or not I usually run a simulation; look at the worst-case scenario and determine if my bankroll can sustain such a hit.

JOB might be a special case. The smaller pays converge pretty quickly which only leaves the royal, so you end up with a bimodal distribution. Sessions where you hit a royal and sessions where you didn't. Without the royal you'll be playing at about a 2.5% house edge, so you'll most likely lose at this promotion but if you do hit a royal you'll be almost $4K ahead. You can estimate the chance of hitting the royal by using the exponential distribution Probability= 1-exp(-1*hands played/cycle length)

I understand the distribution is quite skewed due to RF. Regardless, I still think you can use Kelly in VP (like in a grind-it-out FPDW or 10x points day).

What if you had a similar promotion, but instead of VP it was on BJ? You have to put in some $X of action and you get back some Y% in cash, as long as you hit that $X action. How would you do such a calculation?


Perhaps I'm wrong, but I really don't buy the "do a simulation, see what the worst case scenario is, and see if you BR can sustain such a loss" pitch. It doesn't seem too mathematical. It seems very guess-work like.


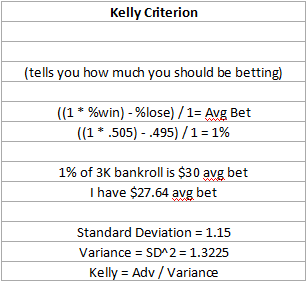
Kelly says EDGE / VARIANCE * BANKROLL = WAGER.

Would it be possible to do something like:

0.0154 / VARIANCE * BANKROLL = 10,000 where 100K is BR and 10K is wager requirement. If I can figure out the variance of the play, then using that formula I could figure out what my minimum required bankroll would be. If the standard deviation is $1169, does that mean the variance is $1169^2 = $1.36 million? That doesn't quite make sense, since variance in the kelly formula is simply a number, while the standard dev (1169) and variance (1.36mil) are dollar figures.

Quote: djatc

Expected loss is a bunch of BS. Well I mean that if you play perfect and hit every hand you are supposed to in your coin in, sure that's what you will lose. My rough guess is that for a $10k coin in on dollars you should take about $2000 with you, half a royal. Of course you can adjust based on the variance of the game. Less on JoB, more on DDB. DW and DB somewhere in between.

I don't remember who or what I was listening to or reading, but I recall recently hearing someone talk about how sometimes it feels like expected value is a figure of our imagination and variance is the only thing that is real. BS or not that is what it feels like most days.