What are the odds of hitting a royal flush with a $4000 bankroll before going bust?

Specifically, I'd like to know the odds on a $1 single line 9/6 JoB machine. Since the max win is $4000, I was wondering what the odds are that you can hit a royal (and at least breaking even) before busting.

Thanks in advance.

very nice question
I think the answer may need to be simulated first
and then see if it can be calculated by normal means, (VP is not normal in the short run)
meaning, 4000/ev = average number of hands

we shall see some opinions


my question back to you

"What do you think are the odds?"
Sally

I don't know the answer but from my own experience, I feel like I busted a thousand times before I hit one royal.

A direct answer, albeit with possible rounding errors, is that the probability of "royal before bust" is a bit more than 53%. With 99.48% of cases resolved, I see 53.07% ending with royals, 46.41% ending in bust.

Currently the unresolved cases are breaking towards the royal at a rate of 22.88%, with that rate dropping.

So, I could estimate the "ending" royal percentage to be slightly less than 53.19%, possibly 53.18%.

This sounds about right. I've been lazy about setting up a sim for it though. Currently traveling and later AL wild card game will be on. Maybe I can get to it tomorrow. Lol

While you guys are doing these simulations, any chance you could plug in $3k? I wouldn't itemize, so the real value of a royal isn't $4k.

Regardless, surprised it's over 50% at $4k.

With $3000, it is looking like a 43.41% chance of a royal before bust.

A royal "cycle" for 9/6 Jacks or Better (40,390.55 hands) is expected to lose $921.10. Thus, one can expect to spend about $4921.10 per royal. Without doing the exact calculations, there are some properties of e that suggest the probability of hitting something within one cycle when it has a very low probability on each hand is approximately 1 - e^(-1), which is about 63.21%. This is the limit as the probability of success on each hand approaches zero.

Perhaps that would then lessen the surprise at the stated percentages for "royal before bust" starting with $4000 or $3000.

Royals went to extra innings tonight with miraculous comeback...will have to sim tomorrow...lol

Quote: tringlomane

Royals went to extra innings tonight with miraculous comeback...will have to sim tomorrow...lol

I guess this was another example of "Royals" before bust! :)

Quote: ahiromu

While you guys are doing these simulations, any chance you could plug in $3k? I wouldn't itemize, so the real value of a royal isn't $4k.

Regardless, surprised it's over 50% at $4k.

well, not that much over
and why surprised?
what did you first think?


real fast sim to see where we bees

added $2k too (I did have it)
$2k I gets 32.8% for Royal with (ruin or royal)
Average hands: 12,675.326
SD: 8,378.1059

$3k I gets 43.2% for Royal with (ruin or royal)
Average hands: 17,585.844
SD: 10,536.0218

$4k: 53.6% for Royal with (ruin or royal)
Average hands: 21,423.531
SD: 13,713.0943

added $6k too (I did have it)
$6k I gets 69.2% for Royal with (ruin or royal)
Average hands: 27192.109
SD: 18552.3528

now to the calculation part for mees

OP came up with a very cool VP question
Sally

Thanks Sally...with other conformation I can be more lazy about confirming the answer...lol

And as for...is there is an "more general way" to calculate this... I'm leaning toward no with "finite" stopping points in terms of bankroll (i.e. hitting a royal, hands played limit, etc). I'd love for someone smarter/more diligent than me to prove me wrong on that.

I did not use simulation. Rather I employed a direct calculation using a state space vector and short Excel macros, using only Paste Special Values, routines to prevent rounding errors from getting out of hand, limiting the maximum possible net wins (not counting a final royal) to $100,000, and extrapolating the remaining probability of transitional states (after a large finite number of hands) to the absorbing states of royal or bust, based on the then current relative rate of change in the two absorbing states:

$3000: 43.4066% (unresolved transition states < 0.0000008)

$4000: 53.1883% (unresolved transition states < 0.000085)

Possible problems with the calculation (other than outright formulaic blunders): Excel does not recognize positive numbers < 2^(-1022) or about 2.2250738585072×10^(-308); instead it substitutes in zero for underflows. So, while it is possible during an exact calculation that takes all possibilities into consideration to have, say, 78 consecutive straight flushes, the probability of such an event is (15,131,134/138,425,211,925)^78 or about 1.036 x 10^(-309). While Excel has no trouble with handling the probability of 77 consecutive straight flushes (9.474E-306), a net win of only $3773, it misses the answer for 78 consecutive and instead returns zero. I imagine but have not checked that such errors will still allow the production of an answer accurate to six places as displayed above.

Additionally when Excel adds up 20,000 numbers of various magnitudes that are supposed to sum to one, it often comes up with sums that are off by some function of "machine epsilon," 2^(-52) or about 2.22 x 10^(-16). Before proceeding, I substitute in numbers that are "percent-to-totaled" to ensure that Excel sees the sum as unity. This also could cause small rounding errors, but hopefully they will be both less than the rounding errors without adjustment, and also will not affect the answer to the precision that is shown.

If this looks difficult, I should say that it was actually slightly easier and took less time to put the spreadsheet together than it was to write this explanation. :) That being said, it does need to run on its own for a few hours before getting these answers.

I never considered using vectors and matrices to do this, but yeah doing it that way would work too. I've messed with those calculations before after I learned how to do them from this site and from the math god, BruceZ.

I needed to use them to help determine the likelihood of ever experiencing the rarest gambling event I ever experienced. I was playing 2-7 triple draw lowball poker, a poker game where 75432 with no flush is the best possible hand. Well on what would have been my favorite uncle's 74th birthday (RIP), I was dealt the hand 4 times in a total stretch of 16 hands. The probability of this hand being dealt at any time is 1 in 2548.

At the time I estimated I had played 300k hands of the game, and the odds of someone playing that much seeing this scenario happen is only 1 in 311,849. You can see more details about this here.

http://forumserver.twoplustwo.com/showpost.php?p=36299004&postcount=17

if you're down to your last $5, you'd still be in the hole even with a royal.

w2-G = 20% fed tax + ~5% state tax (if any)

Quote: 100xOdds

if you're down to your last $5, you'd still be in the hole even with a royal.

w2-G = 20% fed tax + ~5% state tax (if any)

And the $4,000 loss that will offset your $4,000 win. And you break even. Actually you're in the black since you will most likely be using a players card and earning points.

Quote: tringlomane

I never considered using vectors and matrices to do this, but yeah doing it that way would work too. I've messed with those calculations before after I learned how to do them from this site and from the math god, BruceZ.

just to show i can do this, and it was easy

I finally got to do this in Excel with a simple 1602x1602 transition matrix

a friend asked about it with the chance to double the bankroll too B4 ruin
so i had 3 target points (absorbing states)
a quick pic

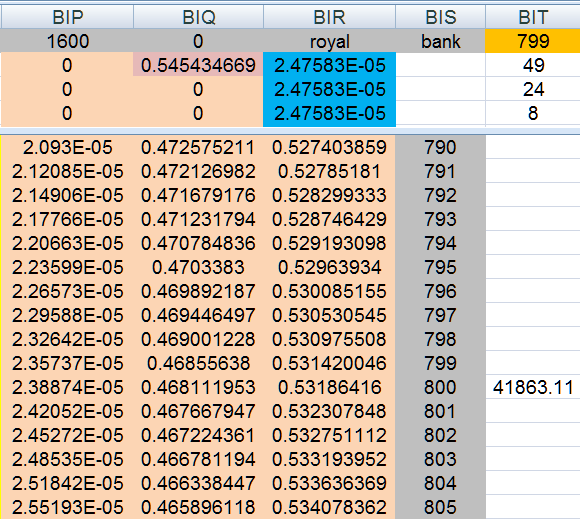
yes, the file is quite large (48.6MB) using (I-S)^-1*T (common stuff computers like to calculate for those that know - no lesson here)

here is the data

12,755.69935 average number of hands
400 units ($2000)
0.315809024 Royal B4 Ruin
To 1600 units: 1 in 8,303,414.132
==================================
OP asked about these two:

17,532.10249 average number of hands
600 units ($3000)
0.434064493 Royal B4 Ruin
To 1600 units: 1 in 588,676.8991

21,482.28457 average number of hands
800 units ($4000)
0.53186416 Royal B4 Ruin
To 1600 units: 1 in 41,863.10776
===================================
24,740.43841 average number of hands
1,000 units ($5000)
0.612530406 Royal B4 Ruin
To 1600 units: 1 in 2,977.585829


this was fun and only about 10 minutes to setup the stage
a macro to fill in 1548 diagonal cells sure helps out
Mully

now to compare with this article
https://wizardofvegas.com/article/introductory-advantage-play2/
"At this point, we're going to determine two things:
What is the probability of hitting a Royal before busting?
What is the probability of profiting?"

if the machine is set to payout 90% you would need a bankroll of 4440. if the machines set to payout 98% lil more than 4000. now thats the total of the machine so if you start and the machine is in the hole it could take more. if you can catch it when it hasn't hit anything then it could take substantially less. if your going to do it i'd watch and see if someone hits some big pays and runs it all off then try. Ig your in vegas find a 100% machine and your odds go up to hitting it before 4000. of course it never has to payout on time it could eat money and then hit 2 jackpots quick. good luck! if you try it hope it hits quick and you make a nice profit!

Quote: champ724

if the machine is set to payout 90% you would need a bankroll of 4440.

for what?
what does the 4400 get you or me or that guy over there?

in other words
what kinda odds does i get to hit a Royal?

or in other words
what be me chances to not get a Royal and bust out your 4400 start bank

Quote: champ724

if the machines set to payout 98% lil more than 4000.

for what again?
is this for the same chance to hit a Royal B4 ruin?

Quote: champ724

now thats the total of the machine so if you start and the machine is in the hole

what hole?
exactly?

Quote: champ724

it could take more. if you can catch it when it hasn't hit anything then it could take substantially less.

so in other words the hot and cold cycles of any vp machine

Quote: champ724

if your going to do it i'd watch and see if someone hits some big pays and runs it all off then try.

that could take some timw
how much time should one give?
this is getting funny to read

Quote: champ724

Ig your in vegas find a 100% machine and your odds go up to hitting it before 4000.

how much up?
can you calculate this for us?

remember OP was talking about 9/6 JOB

Quote: champ724

of course it never has to payout on time

what time schedule is that?
the "average time schedule"

Quote: champ724

it could eat money and then hit 2 jackpots quick.

but really now
what are the chances one vp machine will do exactly that?
1 in 1 million?
1 in 1 billion?
higher?
lower?

more next week

a machine pays out a percentage everyone thinking there is odds for hitting certain hands thats not how they are set to payout when a machine takes in enough to hit a foyal or 4 deuces then it will deal the hand. slot machines poker machines aren't made to lose money. if a machine is set to pay at 90% its not gonna pay 200% it has to take enough money for the machine to make money and be able to pay the 4000

Quote: champ724

if the machine is set to payout 90% you would need a bankroll of 4440. if the machines set to payout 98% lil more than 4000. now thats the total of the machine so if you start and the machine is in the hole it could take more. if you can catch it when it hasn't hit anything then it could take substantially less. if your going to do it i'd watch and see if someone hits some big pays and runs it all off then try. Ig your in vegas find a 100% machine and your odds go up to hitting it before 4000. of course it never has to payout on time it could eat money and then hit 2 jackpots quick. good luck! if you try it hope it hits quick and you make a nice profit!

-100

Quote: champ724

a machine pays out a percentage everyone thinking there is odds for hitting certain hands thats not how they are set to payout when a machine takes in enough to hit a foyal or 4 deuces then it will deal the hand. slot machines poker machines aren't made to lose money. if a machine is set to pay at 90% its not gonna pay 200% it has to take enough money for the machine to make money and be able to pay the 4000

ok
got it now
more like the slots (vp too?) in England i hear, never played them
they have to pay out from what they take in

this could be different in the US
but you say no

thank you for the clear-up

when a vegas slot machine advertises 99% payout that machine has to payout 99% or higher or the casino gets fined so that machine will show payouts 99% and higher could be 99.5 or whatever but the payout doesn;t mean hit ratio. if you put $100 in the machine and you get $99 in hits but you don't cash out and walk away that machine is at 0% so if your playing them first your gonna get alot of play but if the machine took in a million and paid out 999,999 it can pay out 0 for $9,999 and still have a payout ratio of 99% meanwhile if your the guy thinkin you can hit a royal flush with $4000 and the payout is well over the % it can eat your 1k2k3k4k5k6k and still be in compliance with the payout requirement. hands being dealt and the probability of a royal being dealt has no bearing on a video poker machine.

Quote: champ724

if the machine is set to payout 90% you would need a bankroll of 4440. if the machines set to payout 98% lil more than 4000. now thats the total of the machine so if you start and the machine is in the hole it could take more. if you can catch it when it hasn't hit anything then it could take substantially less. if your going to do it i'd watch and see if someone hits some big pays and runs it all off then try. Ig your in vegas find a 100% machine and your odds go up to hitting it before 4000. of course it never has to payout on time it could eat money and then hit 2 jackpots quick. good luck! if you try it hope it hits quick and you make a nice profit!

I don't think this is correct for the vast majority of US machines. There are some fruit machines in the UK that adjust their payouts in a way that might resemble what champ is describing; the Wizard did some pretty detailed reporting on those last year, helped by charliepatrick and I think someone else. He wrote a couple WoO website pages on it if you're interested in that type machine.

My best understanding, and I'd be happy to be corrected on any of this:

US VP machines have paytables based on a 52 card deck. In most states, it's illegal for them not to replicate results achievable by using a real deck. An RNG determines the initial draw and the cards available after that, regardless of what you hold. However, a few states and tribes use bingo results or pull tab results to determine VP results (and also Class II slot results), and so the result will be awarded no matter whether you play your hand the best way or not.

US Class III slot machines (like in Nevada) use an RNG to generate a number that corresponds to a particular result. The RNG cycles some number per second, and your result is decided the nanosecond you press the spin button. The rest is entertainment. The amount each screen or reel set pays has been predetermined; those results show up at a frequency that corresponds with the programmed return of the machine over the long run. The percentage is programmed into an EPROM chip; the distributor can provide a range of EPROM chips, and install whatever percentage the casino wants to offer. Once the chip is in place, the payback percentage doesn't go up and down; it all works off that programmed paytable (which is frequency of occurrence x value of the win).

Quote: beachbumbabs

I don't think this is correct for the vast majority of US machines. There are some fruit machines in the UK that adjust their payouts in a way that might resemble what champ is describing; the Wizard did some pretty detailed reporting on those last year, helped by charliepatrick and I think someone else. He wrote a couple WoO website pages on it if you're interested in that type machine.

My best understanding, and I'd be happy to be corrected on any of this:

US VP machines have paytables based on a 52 card deck. In most states, it's illegal for them not to replicate results achievable by using a real deck. An RNG determines the initial draw and the cards available after that, regardless of what you hold. However, a few states and tribes use bingo results or pull tab results to determine VP results (and also Class II slot results), and so the result will be awarded no matter whether you play your hand the best way or not.

US Class III slot machines (like in Nevada) use an RNG to generate a number that corresponds to a particular result. The RNG cycles some number per second, and your result is decided the nanosecond you press the spin button. The rest is entertainment. The amount each screen or reel set pays has been predetermined; those results show up at a frequency that corresponds with the programmed return of the machine over the long run. The percentage is programmed into an EPROM chip; the distributor can provide a range of EPROM chips, and install whatever percentage the casino wants to offer. Once the chip is in place, the payback percentage doesn't go up and down; it all works off that programmed paytable (which is frequency of occurrence x value of the win).

that is correct us machines cannot replicate results. all taht means is the machine cannot duplicate the card folded. like if you have Ah Kh Qh Jh and a 3d if you fold the 3 of diamonds the rng cannot replicate the 3d back on the board. but the payout % is adjustable on all class 3 machines and that is what determines the payout for that machine some machines are set low (tihgt) and high (loose) video poker machines are set by a percentage just like any other class 3 slot machine and they all have rng the lowest % a machine can be set to i believe is 80% here in PA the Meadows has a pay rate for all machines of 89%. If you wanna advantage get to know a slot supervisor and find out where the loose machines are placed.

While I can't contribute any significant assistance on the answer of the question - the theories of how VP machines work - I'm finding very interesting.

On a 98% machine, I always assumed that over time, given enough hands - if I play 200 hands, with 5 coins per bet, I'd average 980 coins.

(assuming I did that over 30 times)

As for how the machine determines when to pay and when not to - that is the mystery. From everything that I've read, the past has no bearing on the future. Technically, you could get a Royal 5 hands in a row. Odds are against that, of course, but theoretically, it could happen.

Just like yesterday, on the $5 per coin, JoB VP machine at the IP casino in Biloxi, I lost 7 hands in a row. Won a hand with a pair, and then lost 8 or 9 hands in a row. $400 bucks gone in mere minutes.

If only we had a way of knowing. In the late 80's, early 90's, I *seemed* to do real well when the ashtrays were filled with cigarette butts and had stacks of plastic cups (looked like a tight machine where someone had played a long while). With the crazy theory, "it's bound to pay sooner or later", I chose those machines and did pretty well.

But now - I think it's all pretty random. Over time, you'll win for a few minutes, then lose for a few minutes. Up and down. It's all whether you have the bankroll to hold you until the machine starts to win. Even then, you may not win back everything you lost. The only real way to find out is to pay your money and take your chances.