Theoretical Payout on 9/6 JoB with opposite to optimal strategy.

This is a pretty silly question but I'm just curious. What is theoretical payout on a 9/6 JoB machine where the worst possible strategy is used. By worst possible strategy, I mean keeping all cards on a non-winning hand. Not keeping cards winning cards. (ie if dealt a Full House, discard everything. If dealt a pair of Queens, discard the Queens, but keep the other non-winning cards). I think you get the idea, making the worst possible decision on every single hand.

How low does the theoretical payout get? Does it get below 50%?

Quote: etr102

This is a pretty silly question but I'm just curious. What is theoretical payout on a 9/6 JoB machine where the worst possible strategy is used. By worst possible strategy, I mean keeping all cards on a non-winning hand. Not keeping cards winning cards. (ie if dealt a Full House, discard everything. If dealt a pair of Queens, discard the Queens, but keep the other non-winning cards). I think you get the idea, making the worst possible decision on every single hand.

How low does the theoretical payout get? Does it get below 50%?

Far worse than 50%. Consider the "always discard 5" strategy, which is nearly equivalent to playing 5-card stud against a 9/6 JoB paytable. The probabilities for 5-card stud are on the Wizard's site. What is the return of JoB 9/6 vs. that probability distribution?

Now consider how much worse the "worse strategy" would be than "always discard 5". Note that you can actually compute the minimum RTP if you have a VP analyzer. Substitute "min()" for "max()" in the draw evaluation routine and re-run.

I get a return of 2.3717%.

Quote: etr102

if dealt a Full House, discard everything. If dealt a pair of Queens, discard the Queens, but keep the other non-winning cards

You can do much worse than both of those. With the queens, don't keep any singletons Jack or higher. With the full house, keep 2 from the set and 1 from the pair if either is 10 or lower.

Quote: MathExtremist

Note that you can actually compute the minimum RTP if you have a VP analyzer. Substitute "min()" for "max()" in the draw evaluation routine and re-run.

Or just use https://wizardofodds.com/games/video-poker/analyzer/ and put in negative numbers for the pays. The return will show a minus sign.

Quote: miplet

Or just use https://wizardofodds.com/games/video-poker/analyzer/ and put in negative numbers for the pays. The return will show a minus sign.

That technique produced different results than the other method (selecting the play with the lowest return, which is the method I used to produce the table above).

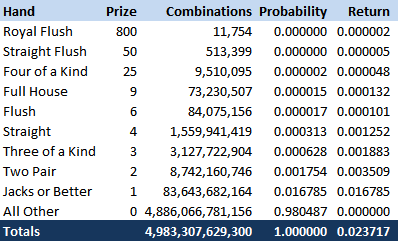
Quote: JB

I get a return of 2.3717%.

Does that account for the autohold on the dealt royal flush?

Excellent point. No it does not. So the actual return would be no more than 0.00123126 higher than the figure shown in the table.

Also, using miplet's suggested method produces a fairly close estimate, but plugging in the strategy results of using negative payoffs for winning hands into the 9/6 paytable produces a return of 2.8736% which is close, but still higher than using the real paytable and selecting the play that returns the least for each hand. Again, the 2.8736% does not include the automatic/mandatory return from dealt royals; it assumes a dealt royal can be broken up.

Quote: JB

Excellent point. No it does not. So the actual return would be no more than 0.00123126 higher than the figure shown in the table.

Also, using miplet's suggested method produces a fairly close estimate, but plugging in the strategy results of using negative payoffs for winning hands into the 9/6 paytable produces a return of 2.8736% which is close, but still higher than using the real paytable and selecting the play that returns the least for each hand. Again, the 2.8736% does not include the automatic/mandatory return from dealt royals; it assumes a dealt royal can be broken up.

I'm getting 2.3717 using negative pays

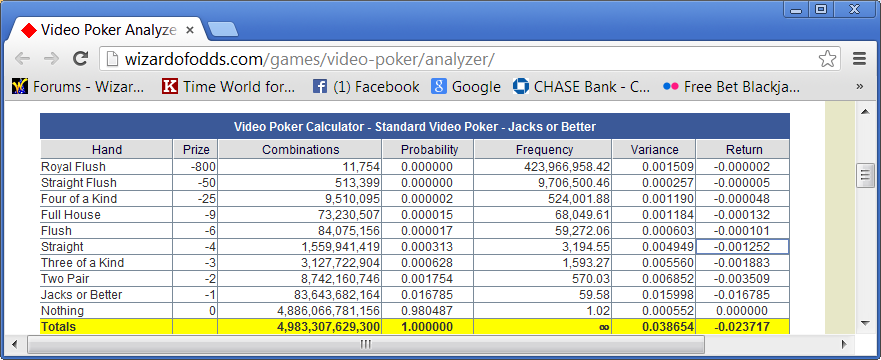
I get the same using your video poker wizard app.

Now I am curious as to why you asked this question.

Quote: miplet

I'm getting 2.3717 using negative pays
I get the same using your video poker wizard app.

That explains it. I used -1 for each payoff instead of the actual payoff multiplied by -1. My mistake.

You're touching on something I've wondered about for a long time, and maybe I just don't understand the RTP jargon. (Assuming that's Return To Player or something analagous.) Is it possible on a VP machine to go so far off (like you're suggesting) that it starts putting extra values, changing the drawn cards you would receive for optimal play, just to maintain a minimum payout? Does it track the result of player choices and change the cards to suit pre-set values?

I'm thinking that maybe the RNG doesn't generate actual card values, but generates a number equating to a programmed win value, then displays cards that, no matter what you hold or don't hold, it will put cards up there that equate to that value. Is that how it actually works, or can you play so badly that you drop below a mandated minimum payout?

Seems like, if you can affect it like this, you could load it with minimum bets and horrible play for a few hundred hands, and then bet big while it corrects to its programmed payout percentages....

Quote: beachbumbabs

You're touching on something I've wondered about for a long time, and maybe I just don't understand the RTP jargon. (Assuming that's Return To Player or something analagous.) Is it possible on a VP machine to go so far off (like you're suggesting) that it starts putting extra values, changing the drawn cards you would receive for optimal play, just to maintain a minimum payout? Does it track the result of player choices and change the cards to suit pre-set values?

I seriously doubt that, especially in Nevada and many other jurisdictions in which such a machine is legally required to deal a random, fair and true deck of cards. However, if the machine were inclined to, "Self-correct," the easiest way for it to do so would be to deal out a Natural Royal at a certain threshold.

Quote:

I'm thinking that maybe the RNG doesn't generate actual card values, but generates a number equating to a programmed win value, then displays cards that, no matter what you hold or don't hold, it will put cards up there that equate to that value. Is that how it actually works, or can you play so badly that you drop below a mandated minimum payout?

That's very close to the way a Class II VLT (Video Lottery Terminal) works, but in jurisdictions that operate those, the expectation is not a fair deck of cards. It also doesn't matter what you hold or don't hold, as a, "Genie," will even change your cards on some machines.

In terms of the machines that deal a true, random deck, yes, the machine could theoretically drop below the mandated minimum payout...however, I believe that the machine (with optimal strategy) being well above such would suffice. I could be wrong.

Quote:

Seems like, if you can affect it like this, you could load it with minimum bets and horrible play for a few hundred hands, and then bet big while it corrects to its programmed payout percentages....

That's the thing, the payout percentage is a theoretical based on the payout table. The only thing the machine is programmed to do is deal a true and random game from a complete deck of cards.

Thanks, Mission! I appreciate the response.

Always a pleasure!

Actually, if you want some more information on how Class II VLT's work, check out one of my responses to a response in my Scioto Downs blog, it's the last response.

Quote: djatc

Now I am curious as to why you asked this question.

My mind works in strange ways. The 'math' side of gambling fascinates me, so I was hoping somebody could calculate this. It's actually much worse than I thought.

I appreciate all of those who replied.

Quote: beachbumbabs

You're touching on something I've wondered about for a long time, and maybe I just don't understand the RTP jargon. (Assuming that's Return To Player or something analagous.) Is it possible on a VP machine to go so far off (like you're suggesting) that it starts putting extra values, changing the drawn cards you would receive for optimal play, just to maintain a minimum payout? Does it track the result of player choices and change the cards to suit pre-set values?

I'm thinking that maybe the RNG doesn't generate actual card values, but generates a number equating to a programmed win value, then displays cards that, no matter what you hold or don't hold, it will put cards up there that equate to that value. Is that how it actually works, or can you play so badly that you drop below a mandated minimum payout?

Seems like, if you can affect it like this, you could load it with minimum bets and horrible play for a few hundred hands, and then bet big while it corrects to its programmed payout percentages....

In NV, MO, MS, NJ, IA, IN, IL, and a ton of other states I am leaving out due to laziness, the minimum return requirement needs to be only met when optimal strategy is used. If you feel playing so badly to return 2.37%, that's up to you and the casino is not responsible to provide a better payout.

Quote: tringlomane

In NV, MO, MS, NJ, IA, IN, IL, and a ton of other states I am leaving out due to laziness, the minimum return requirement needs to be only met when optimal strategy is used. If you feel playing so badly to return 2.37%, that's up to you and the casino is not responsible to provide a better payout.

I don't think this is totally true where skill is involved. lets say they Minimum payback in NV is 75% I don't believe they can put in a Video poker machine that is exactly 75%. I believe they must base it on how the average player would play. For instance they could not make a game that had 1 and only 1 payback lets say a large amount for a straight flush and they set the payout to total exactly 75% payback, The strategy would be to complex for a normal person to play, almost guaranteeing the machine would fall below the minimum requirement.

Quote: AxelWolf

I don't think this is totally true where skill is involved. lets say they Minimum payback in NV is 75% I don't believe they can put in a Video poker machine that is exactly 75%. I believe they must base it on how the average player would play. For instance they could not make a game that had 1 and only 1 payback lets say a large amount for a straight flush and they set the payout to total exactly 75% payback, The strategy would be to complex for a normal person to play, almost guaranteeing the machine would fall below the minimum requirement.

Playing a machine like that would guarantee the actual return would be below 75% if the optimal percentage is 75.00%, but the law as currently written in Nevada, the actual return on skill machines are irrelevant.

14.040 Minimum standards for gaming devices. All gaming devices submitted for approval:
1. Must theoretically pay out a mathematically demonstrable percentage of all amounts
wagered, which must not be less than 75 percent for each wager available for play on the device.
(a) Gaming devices that may be affected by player skill must meet this standard when using a
method of play that will provide the greatest return to the player over a period of continuous play.

http://gaming.nv.gov/modules/showdocument.aspx?documentid=2921

Also GLI standards confirm this:

http://www.gaminglabs.com/downloads/GLI%20Standards/Bill%20E%202011/GLI-11%20v2.1.pdf

3.4.1 Software Requirements for Percentage Payout. Each game shall theoretically payout a
minimum of seventy-five percent (75%) during the expected lifetime of the game (i.e.,
progressives, bonus systems, merchandise, etc. shall not be included in the percentage payout if
they are external to the game).
a) Optimum Play Used for Skill Games. Gaming devices that may be affected by player
skill shall meet the requirement of this section when using a method of play that will
provide the greatest return to the player over a period of continuous play.

There is no rule mandating that skill-based electronic gaming machines must return 75% to the player in actual use. They must only be expected to do so under optimal play.

So NV casinos could offer a game like this if they wished:

Royal 800
SF 65
4K 25
FH 6
Flush 5
Str. 4
3K 2
2P 1
JoB 1

That paytable returns 75.06% optimally.

And depending on how strict gaming is on rounding, they possibly could offer this game with a SF of 60 because the return of that is 74.9995%...haha They definitely can offer 61 for 1 on SF (75.01%).

The good news is, competition in the market is too high in NV to offer such a poor game. And competition is generally too high in the rest of the country where states offer 80 to 90% minimum returns. And even if they did offer the game ignoring any competition issues, it would likely to be stupid to do so because you would lose so consistently and quickly, even the biggest addicts won't play. The worst game I have actually have seen in the casinos so far might still be 6/5 DDB (94.66% max), I have heard the D offers 8/5 Bonus with a 1 for 1 2 pair payout though (86.31% max).

Supposedly the minimum payback on VP is supposed to be 2% higher than the minimum in NJ by an unwritten rule referenced in Steve Bourie's "Are Slot Machines Honest".

Quote: onenickelmiracle

Supposedly the minimum payback is supposed to be 2% higher than the minimum in NJ by an unwritten rule referenced in Steve Bourie's "Are Slot Machines Honest".

In reality, this unwritten rule is probably always enforced in practice. The terrible payouts at the D long bar still qualify under this rule.

Quote: tringlomane

In reality, this unwritten rule is probably always enforced in practice. The terrible payouts at the D long bar still qualify under this rule.

I had meant to specify on VP machines and have since edited.

Quote: tringlomane

Playing a machine like that would guarantee the actual return would be below 75% if the optimal percentage is 75.00%, but the law as currently written in Nevada, the actual return on skill machines are irrelevant.

14.040 Minimum standards for gaming devices. All gaming devices submitted for approval:
1. Must theoretically pay out a mathematically demonstrable percentage of all amounts
wagered, which must not be less than 75 percent for each wager available for play on the device.
(a) Gaming devices that may be affected by player skill must meet this standard when using a
method of play that will provide the greatest return to the player over a period of continuous play.

http://gaming.nv.gov/modules/showdocument.aspx?documentid=2921

Also GLI standards confirm this:

http://www.gaminglabs.com/downloads/GLI%20Standards/Bill%20E%202011/GLI-11%20v2.1.pdf

3.4.1 Software Requirements for Percentage Payout. Each game shall theoretically payout a
minimum of seventy-five percent (75%) during the expected lifetime of the game (i.e.,
progressives, bonus systems, merchandise, etc. shall not be included in the percentage payout if
they are external to the game).
a) Optimum Play Used for Skill Games. Gaming devices that may be affected by player
skill shall meet the requirement of this section when using a method of play that will
provide the greatest return to the player over a period of continuous play.

There is no rule mandating that skill-based electronic gaming machines must return 75% to the player in actual use. They must only be expected to do so under optimal play.

So NV casinos could offer a game like this if they wished:

Royal 800
SF 65
4K 25
FH 6
Flush 5
Str. 4
3K 2
2P 1
JoB 1

That paytable returns 75.06% optimally.

And depending on how strict gaming is on rounding, they possibly could offer this game with a SF of 60 because the return of that is 74.9995%...haha They definitely can offer 61 for 1 on SF (75.01%).

The good news is, competition in the market is too high in NV to offer such a poor game. And competition is generally too high in the rest of the country where states offer 80 to 90% minimum returns. And even if they did offer the game ignoring any competition issues, it would likely to be stupid to do so because you would lose so consistently and quickly, even the biggest addicts won't play. The worst game I have actually have seen in the casinos so far might still be 6/5 DDB (94.66% max), I have heard the D offers 8/5 Bonus with a 1 for 1 2 pair payout though (86.31% max).

Is that a real payable somewhere? Whats the lowest payback IGT offers on VP in NV? I had no clue the D had a VP game plat payed so horrible that's absolutely disgusting. I wonder how much action they get? Don't answer it may give other bars ideas.

I have see information on how all this is written however I was told they would not approve anything with a strategy that was so complex that it would defiantly fall below the %75 with average play over a long period of time. Certainly that dose not include the blind guy who just hits random buttons. Hell if they allowed this Someone could just come up with some 101% chess type VP game or Tetris VP ( advertising 101%payback) that only a few people in the world could play it optimally. I understand that they can call something 99.9% payback only with optimal play

Quote: AxelWolf

Is that a real payable somewhere? Whats the lowest payback IGT offers on VP in NV? I had no clue the D had a VP game plat payed so horrible that's absolutely disgusting. I wonder how much action they get? Don't answer it may give other bars ideas.

I have see information on how all this is written however I was told they would not approve anything with a strategy that was so complex that it would defiantly fall below the %75 with average play over a long period of time. Certainly that dose not include the blind guy who just hits random buttons. Hell if they allowed this Someone could just come up with some 101% chess type VP game or Tetris VP ( advertising 101%payback) that only a few people in the world could play it optimally. I understand that they can call something 99.9% payback only with optimal play

Oh hell no, I made that paytable up to show what a minimally legal paytable would possibly look like, don't worry. :)

As far as the D is concerned, I have also heard the same bar offers 8/6 Bonus Poker Deluxe (98.49%), so not all games there are bad. But that bonus game may be one of the worst in the country. I have yet to see worse than 6/5 DDB myself.

Would the game have to return 75%+ for all possible coin in options or would number of coins played be a choice just like throwing away a dealt royal is a choice?

Quote: soulhunt79

Would the game have to return 75%+ for all possible coin in options or would number of coins played be a choice just like throwing away a dealt royal is a choice?

All coin options. So the table I wrote as an example wouldn't work if the Royal paid 250 for 1.

I stopped off a bar in Oregon and saw a really horrible paytable, and it's a VLT. Something like 2400 coins for a royal on a 10 coin game. Nobody was playing it but it probably gets some dummies that hop on these things.

Quote: AxelWolf

I don't think this is totally true where skill is involved. lets say they Minimum payback in NV is 75% I don't believe they can put in a Video poker machine that is exactly 75%. I believe they must base it on how the average player would play. For instance they could not make a game that had 1 and only 1 payback lets say a large amount for a straight flush and they set the payout to total exactly 75% payback, The strategy would be to complex for a normal person to play, almost guaranteeing the machine would fall below the minimum requirement.

Paying 2180 for Royal and Straight Flushes would pay back 75.0014%. The strategy isn't that hard either. 2900 gets you to 99.7726

Quote: djatc

I stopped off a bar in Oregon and saw a really horrible paytable, and it's a VLT. Something like 2400 coins for a royal on a 10 coin game. Nobody was playing it but it probably gets some dummies that hop on these things.

Yeah, Oregon VLTs are generally horrible (often 91% or so), but they are at least from a fair poker deck unlike some VLTs. Illinois VGTs in bars/restaurants caps wins at 2000 quarters and you can bet up to 8 quarters. With the max bet, usually any straight flush wins $500 as well because the overall return of the game needs to increase with bigger wagers. Illinois also offers better games than Oregon, including 6/5 Bonus, 6/5 Super DDB, and 7/5 Super Aces, and even a $500 Royal version of Shockwave that's about 97%. Most ppl play slots on these though, as they do in Oregon.

Quote: miplet

Paying 2180 for Royal and Straight Flushes would pay back 75.0014%. The strategy isn't that hard either. 2900 gets you to 99.7726

Yeah the strategy isn't hard when a Straight flush is the only winning hand. It's when you make higher SF payouts mix in with all the other payouts that makes the game more difficult. Here is the strategy when you max bet the best game Illinois bars have to offer. It's still easier than All American probably, but the high straight flush makes things more tricky.

Royal Flush 250
Straight Flush 250
Four Aces 250
Four 2's, 3's, 4's 90
Four 5's through K's 55
Full House 7
Flush 5
Straight 4
Three of a Kind 3
Two Pair 1
Jacks or Better 1
Nothing 0
Return: 97.97%

The following table shows the basic strategy:

Basic Strategy
Type of Play Play Details
4 of a Kind AAAA
Pat Hand Four 5's through K's; Four 2's, 3's, 4's; Straight Flush; Royal Flush
3 of a Kind AAA
4 to a Straight Flush A234; A235; A245; A345; 2345; 2346; 2356; 2456; 3456; 3457; 3467; 4567...
Pat Hand Full House
4 to a Royal Flush TJQA; TJQK; TJKA; TQKA; JQKA
4 to a Straight Flush 9TJK; 9JQK
4 to a Straight Flush 79TJ; 89JQ
4 to a Straight Flush 679T; 789J
4 to a Straight Flush 3567; 5789; 678T; 689T; 78TJ; 89TQ; 8TJQ; 9TQK
3 of a Kind 222; 333; 444; 555; 666; 777; 888; 999; TTT; JJJ; QQQ; KKK
Pat Hand Straight; Flush
1 Pair AA
2 Pair 2233; 2244; 2255; 2266; 2277; 2288; 2299; 22TT; 22JJ; 22QQ; 22KK; 3344...
1 Pair JJ; QQ; KK
4 to a Flush 2347; 2348; 2349; 234T; 234J; 234Q; 234K; 2357; 2358; 2359; 235T; 235J...
3 to a Royal Flush TJQ; TJK; TQK; JQA; JQK; JKA; QKA
3 to a Straight Flush 234; 345; 346; 456; 567; 678; 679; 689; 789; 78T; 79T; 89T; 89J; 8TJ...
1 Pair 44
3 to a Straight Flush 235; 356; 568; 578
1 Pair 33
3 to a Straight Flush 245; 457; 467
1 Pair 22
4 to a Straight 9TJQ; TJQK
3 to a Royal Flush TJA; TQA; TKA
3 to a Straight Flush 8JQ; 9JK; 9QK
4 to a Straight 89TJ; JQKA
1 Pair 55; 66; 77; 88; 99; TT
4 to a Straight 2345; 3456; 4567; 5678; 6789; 789T
3 to a Straight Flush A23; A24; A25; A34; A35; A45; 569; 579; 589; 67T; 68T; 69T; 78J; 79J...
2 to a Royal Flush JQ
3 to a Straight Flush 236; 246; 256; 347; 357; 367; 458; 468; 478
4 to a Straight TJQA; TQKA
4 to a Straight 8TJQ; 9JQK; TJKA
2 to a Royal Flush JA; JK; QA; QK; KA
3 to a Straight JQK
4 to a Straight 89JQ; 9TJK; 9TQK
2 to a Straight JQ
Single Card an Ace
2 to a Royal Flush TJ
2 to a Straight JK; QK
Single Card a Jack; a King
2 to a Royal Flush TQ
Single Card a Queen
4 to a Straight 2346; 2356; 2456; 3457; 3467; 3567; 4568; 4578; 4678; 5679; 5689; 5789...
2 to a Straight Flush 9T
2 to a Straight Flush 45
2 to a Straight Flush 89
Garbage Discard everything