June 26th, 2025 at 5:59:46 PM
permalink
32 Cards is a new table game I noticed at the Slotastic Internet casino. Here are the rules.
Let's consider this screenshot as an example.
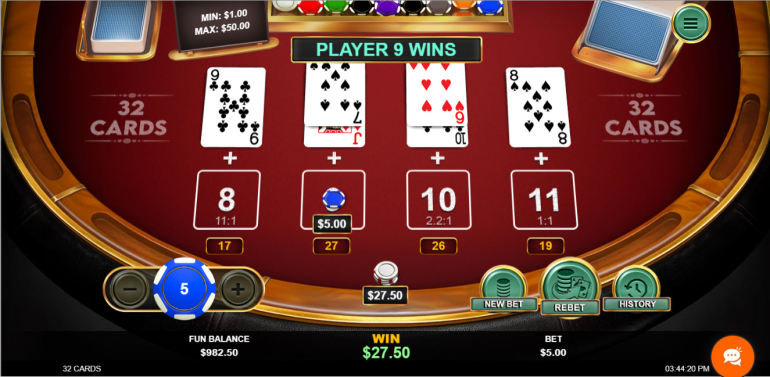
After the initial four cards were deal the scores were:
Spot 8 = 17
Spot 9 = 20
Spot 10 = 20
Spot 11 = 19
So, there was a tie between spots 8 and 9. After an additional card was dealt to the two tying spots, the adjusted scores were:
Spot 8 = 17
Spot 9 = 27
Spot 10 = 26
Spot 11 = 19
So, spot 9 won.
Here is my unconfirmed analysis*.
*: Updated 5:55 AM, 6/27/25
I welcome the other math wizards of the forum to see what they get. I could be wrong, but feel pretty good about these numbers.
Thank you.
- A 32-card deck is used, with ranks only 6 to K.
- Point values are as follows: 6 to 10 = pip value, J = 11, Q = 12, K = 13
- There are four betting spots titled 8, 9, 10, 11
- After betting is closed, the dealer will deal a card to each of the four betting spots.
- The score of each betting spot shall be the sum of the card dealt to that betting spot and the number of that betting spot. For example, if betting spot 8 got dealt a Q, then it would have 8+12=20 points.
- The spot with the greatest points shall win.
- In the event of a tie, additional cards shall be dealt to those positions that were involved in the tie until the tie is broken.
- Winning bets on spot 8 pays 11 to 1.
- Winning bets on spot 9 pays 4.5 to 1.
- Winning bets on spot 10 pays 2.2 to 1.
- Winning bets on spot 11 pays 1 to 1.
Let's consider this screenshot as an example.

After the initial four cards were deal the scores were:
Spot 8 = 17
Spot 9 = 20
Spot 10 = 20
Spot 11 = 19
So, there was a tie between spots 8 and 9. After an additional card was dealt to the two tying spots, the adjusted scores were:
Spot 8 = 17
Spot 9 = 27
Spot 10 = 26
Spot 11 = 19
So, spot 9 won.
Here is my unconfirmed analysis*.
| Winner | Pays | Probability | Return |
|---|---|---|---|
| 8 | 11 | 0.078328 | -0.060067 |
| 9 | 4.5 | 0.163787 | -0.099172 |
| 10 | 2.2 | 0.293023 | -0.062326 |
| 11 | 1 | 0.464862 | -0.070276 |
*: Updated 5:55 AM, 6/27/25
I welcome the other math wizards of the forum to see what they get. I could be wrong, but feel pretty good about these numbers.
Thank you.
Last edited by: Wizard on Jun 27, 2025
"My life is spent in one long effort to escape from the commonplace of existence. These little problems help me to do so." -- Sherlock Holmes
June 27th, 2025 at 1:26:07 AM
permalink
Wiz,
Two corrections:
The score for spot 8 is actually 8 + 9 = 17.
Typo: "tieing" should be "tying".
Dog Hand
Two corrections:
The score for spot 8 is actually 8 + 9 = 17.
Typo: "tieing" should be "tying".
Dog Hand
June 27th, 2025 at 2:41:00 AM
permalink
Would it be possible to run out of cards with an unresolved tie? I don't see any contingency for that. It might be ruled out by the starting point values on the felt.
June 27th, 2025 at 4:13:57 AM
permalink
Quote: AutomaticMonkeyWould it be possible to run out of cards with an unresolved tie? I don't see any contingency for that. It might be ruled out by the starting point values on the felt.
link to original post
Since this is an Internet casino, I'm sure they shuffle after every bet. That would make it extremely unlikely to run out of cards. 18 yo's kind of unlikely.
"My life is spent in one long effort to escape from the commonplace of existence. These little problems help me to do so." -- Sherlock Holmes
June 27th, 2025 at 1:27:54 PM
permalink
Quote: AutomaticMonkeyWould it be possible to run out of cards with an unresolved tie? I don't see any contingency for that. It might be ruled out by the starting point values on the felt.
link to original post
AutomaticMonkey,
It is possible. Say the first 4 cards are 6, 5, 6, 5. Now both the 10-spot and 11-spot have 16. Now they each draw a 5 to tie at 21, then each a 6 to tie at 27, then two rounds each of 7's, two rounds of 8's, etc., until the last round where they each draw a K.
As the Wiz mentioned, we're talking 18 yo territory for the probability.
Dog Hand
June 27th, 2025 at 3:20:50 PM
permalink
Quote: Wizard
Winner Pays Probability Return 8 11 0.078328 -0.060067 9 4.5 0.163787 -0.099172 10 2.2 0.293023 -0.062326 11 1 0.464862 -0.070276
link to original post
My calculations gave the same numbers.
June 29th, 2025 at 8:17:46 AM
permalink
Here's what I get, with rational numbers - my numbers match everybody else's:
| Winner | Probabability | Return | ||
|---|---|---|---|---|
| 8 | 845/10,788 | 0.078327771598072 | 845/899 | 0.939933259176864 |
| 9 | 6626/40,455 | 0.16378692374243 | 36,443/40,455 | 0.900828080583365 |
| 10 | 47,417/161,820 | 0.293023112099864 | 189,668/202,275 | 0.937673958719564 |
| 11 | 18,806/40,455 | 0.464862192559635 | 37,612/40,455 | 0.929724385119269 |


