Thread Rating:
- Field trial started Nov 4 at the Flamingo
- Game is by Creative Dream Gaming
I did a search on both the game and company and couldn't find anything useful.
I have no imminent Strip visits planned. If anybody has a chance to report on the rules, please do. Don't just grab a rule card, but note any pay tables on the felt.
This game is having a trial at the Flamingo. The Flamingo is part of a much larger group of casinos. Did the management of the Flamingo decide to give it a trial or did the parent company decide and then simply assign the trial to one of its casinos? Are decisions made on the casino level or does the national company force games on the casino? Can the Director of Tables games at a casino choose to try out a game or is that decision made for him at a higher level
Are games ever tried in multiple casinos with slight variations? Might a game be given a trial in Nevada with one paytable and also in New Jersey with a different pay scale?
Does any one casino have a reputation for being the place for trying out new games.?
Quote: billryanThis seems like a good place to ask about field trials.
This game is having a trial at the Flamingo. The Flamingo is part of a much larger group of casinos. Did the management of the Flamingo decide to give it a trial or did the parent company decide and then simply assign the trial to one of its casinos? Are decisions made on the casino level or does the national company force games on the casino? Can the Director of Tables games at a casino choose to try out a game or is that decision made for him at a higher level
Are games ever tried in multiple casinos with slight variations? Might a game be given a trial in Nevada with one paytable and also in New Jersey with a different pay scale?
Does any one casino have a reputation for being the place for trying out new games.?
link to original post
My experience is that if a Table Games manager asks the parent to trial a game they will usually let the requestor have the trial.
To get more specific, I think there are three groups of Caesars properties in Vegas, with a single person overseeing each group:
Group 1: Ballys, Paris, Planet
Group 2: Cromwell, Harrahs, Linq, Flamingo
Group 3: Caesars Palace
I also assume that if either the player or the dealer has multiple straights, only the longest one counts in terms of determining the winner (e.g. if the player has 9 8 7 6 4 3 2 and the dealer has 9 8 7 6 A K 3, it is a push as both players have a 9-high 4-straight even though the player's "second longest straight" is a 4-high 3-straight compared to the dealer's Ace-high 2-straight).
Quote: ThatDonGuy#16 needs to change the name of the bonus from "Straight Bonus" to "Straight Flush Bonus"
Thanks, fixed.
Quote:I also assume that if either the player or the dealer has multiple straights, only the longest one counts in terms of determining the winner (e.g. if the player has 9 8 7 6 4 3 2 and the dealer has 9 8 7 6 A K 3, it is a push as both players have a 9-high 4-straight even though the player's "second longest straight" is a 4-high 3-straight compared to the dealer's Ace-high 2-straight).
link to original post
That is correct, only the highest straight in a given hand counts. The other cards don't matter.
Quote: GialmereWas it any fun? It sounds frustrating what with all the cards involved, three of which only apply to one of the side bets. And really? You have to pay extra to get the namesake "second chance"?
link to original post
It's a pretty simple game and goes slow. The other players at the table seemed to like it.
Once I had a six-card straight, so I made the 4x raise. As the rules state, with a 6- or 7-card straight, the raise pays 2 to 1. However, the dealer didn't qualify, so I won the Ante only. I would have likely won 8x the Ante had the dealer qualified. Same frustrating problem as in Caribbean Stud. I think one of the side bets should be based on the straight value of the player's hand only. Of course, I wouldn't have made it, but I could see other players not liking missing a big payday because the dealer didn't qualify.
Bottom line is a house edge of 2.81%.
Quote: WizardI have updated my page on Keep it Straight Second Chance to include a strategy and house edge. I welcome all comments and especially a verification.
Bottom line is a house edge of 2.81%.
link to original post
I am getting only 2.77% as the house edge, and I have "raise 2x" on J-10-9
Question: can the raise be any amount between 2x and 4x, or is it limited to, say, 2x, 3x, and 4x? This could affect the house edge.
EDIT: I don't think so, and here's why:
Let the ante bet be 1, and the raise bet be B
For any particular player hand, let W, T, L, and Q be the number of dealer hands that are player wins, ties, losses, and non-qualified, respectively
The value of the hand (for hands less than a 6-straight) is ((B + 1) W - (B + 1) L + Q) / (W + T + L + Q)
= ((B + 1) (W - L) + Q) / (W + T + L + Q)
= B (W - L) / (W + T + L + Q) + (W - L + Q) / (W + T + L + Q)
If W > L, then this is positive, and since it increases as B increases, the bet should be the maximum (raise 4).
If W < L, then increasing B will only increase the amount multiplied by (W - L), which is negative, so it decreases the overall hand value; therefore, the bet should be the minimum (raise 2).
Quote: ThatDonGuyQuote: WizardI have updated my page on Keep it Straight Second Chance to include a strategy and house edge. I welcome all comments and especially a verification.
Bottom line is a house edge of 2.81%.
link to original post
I am getting only 2.77% as the house edge, and I have "raise 2x" on J-10-9
Well, based on playing the game for an hour, folding on 10-9-8 just doesn't feel right to me.
Perhaps what we could do is make a table of the probability of each hand from A-2-3 to 89TJQKA, just to make sure we're both scoring correctly.
Quote:Question: can the raise be any amount between 2x and 4x, or is it limited to, say, 2x, 3x, and 4x? This could affect the house edge.
link to original post
I think so, but I think there is no situation where the player should bet anything in the middle. For the same reason you should never bet 3x on the Big raise in Ultimate Texas Hold 'Em and never double for less in blackjack.
Quote: WizardQuote: ThatDonGuy
I am getting only 2.77% as the house edge, and I have "raise 2x" on J-10-9
Well, based on playing the game for an hour, folding on 10-9-8 just doesn't feel right to me.
You misunderstand. Here's what I get for the strategy:
Fold with A-2-3 or less (we agree on this)
Raise 2x with 2-3-4 through 9-10-Jack
Raise 4x with 10-Jack-Queen or higher
The only difference between your strategy and mine is, with 9-10-Jack, you raise 4x, while I raise only 2x.
I think 9-10-Jack is the one hand where, while a 4x raise has a positive value, a 2x raise has a higher positive value.
Quote: WizardPerhaps what we could do is make a table of the probability of each hand from A-2-3 to 89TJQKA, just to make sure we're both scoring correctly.
Here's what I have:
Player Hand is straight size / high card (e.g. "3/6" is 4-5-6; "6/Queen" is 7-8-9-10-J-Q)
| Player Hand | Wins | Ties | Losses | Not Qualified |
|---|---|---|---|---|
| 1 / 4 | 0 | 0 | 198069616 | 164967344 |
| 1 / 5 | 0 | 0 | 365570736 | 360503184 |
| 1 / 6 | 0 | 0 | 19520497584 | 16420161456 |
| 1 / 7 | 0 | 0 | 55545830512 | 50460961808 |
| 1 / 8 | 0 | 0 | 314692597808 | 273790314352 |
| 1 / 9 | 0 | 0 | 984204417776 | 876723039184 |
| 1 / 10 | 0 | 0 | 2958245399728 | 2620543564592 |
| 1 / Jack | 0 | 0 | 7782579953008 | 6892826118032 |
| 1 / Queen | 0 | 0 | 18275762169936 | 16759119654864 |
| 1 / King | 0 | 0 | 41674033200720 | 35490924795120 |
| 1 / Ace | 0 | 0 | 41059743592160 | 36105214403680 |
| 2 / 2 | 0 | 0 | 44610965969072 | 36837465117808 |
| 2 / 3 | 0 | 0 | 43996676360512 | 37451754726368 |
| 2 / 4 | 0 | 0 | 43393123341120 | 38055307745760 |
| 2 / 5 | 0 | 0 | 59393789136160 | 49802282877440 |
| 2 / 6 | 0 | 0 | 68471320300064 | 58272506212096 |
| 2 / 7 | 0 | 0 | 79711944988960 | 67739509721600 |
| 2 / 8 | 0 | 0 | 92749767257120 | 78569189351680 |
| 2 / 9 | 0 | 0 | 107025353408288 | 90577479104512 |
| 2 / 10 | 0 | 0 | 122842149775136 | 104204432341504 |
| 2 / Jack | 0 | 0 | 139204362311968 | 116542469714432 |
| 2 / Queen | 0 | 0 | 161730405228544 | 139050435611936 |
| 2 / King | 0 | 0 | 163301281400704 | 137479559439776 |
| 2 / Ace | 0 | 0 | 253210460166480 | 203507824324560 |
| 3 / 3 | 0 | 4531785933504 | 119152851925072 | 99010946292464 |
| 3 / 4 | 4937606600688 | 2043071808000 | 78482382102768 | 70474383139104 |
| 3 / 5 | 9403737867760 | 2043071808000 | 73143102616752 | 71347531358048 |
| 3 / 6 | 15219221704432 | 2181661757952 | 70945643888048 | 72237789388128 |
| 3 / 7 | 19356746324720 | 2326052037120 | 68859340753584 | 74689050711136 |
| 3 / 8 | 24810707292400 | 2451282620928 | 65426306069680 | 76446267237472 |
| 3 / 9 | 30571966945008 | 2580979352064 | 61662705962672 | 78222284354656 |
| 3 / 10 | 36717030481136 | 2713496621568 | 57547832338608 | 79962950567008 |
| 3 / Jack | 43275945038576 | 2875508851200 | 53816097788336 | 81620631418208 |
| 3 / Queen | 49156738770160 | 2847940624896 | 46222158853552 | 82617845153632 |
| 3 / King | 55339115714032 | 2847940624896 | 41042377966320 | 81615249096992 |
| 3 / Ace | 91515553117552 | 7136105303232 | 53659705526496 | 121476589806320 |
| 4 / 4 | 35606078512512 | 817952052096 | 18530321524608 | 43379291044224 |
| 4 / 5 | 26359460499776 | 390692232576 | 12118742943104 | 31606743295424 |
| 4 / 6 | 27156018204736 | 390692232576 | 10891206237824 | 32037722295744 |
| 4 / 7 | 28683747889984 | 390692232576 | 9844450879104 | 31556747969216 |
| 4 / 8 | 29524904895296 | 390692232576 | 8872824096384 | 31687217746624 |
| 4 / 9 | 30387907076928 | 390692232576 | 7993862964864 | 31703176696512 |
| 4 / 10 | 31307005764416 | 390692232576 | 7090723227264 | 31687217746624 |
| 4 / Jack | 32612695188288 | 390692232576 | 5915503580800 | 31556747969216 |
| 4 / Queen | 33012332780864 | 390692232576 | 5034891661696 | 32037722295744 |
| 4 / King | 34042796541504 | 390692232576 | 4435406901376 | 31606743295424 |
| 4 / Ace | 49160334310400 | 832510825344 | 5383499680000 | 43700798011776 |
| 5 / 5 | 14485474900736 | 62122913280 | 1502832944128 | 12551073098496 |
| 5 / 6 | 11363938352384 | 36245048832 | 1048888380416 | 10018559598848 |
| 5 / 7 | 11361375768832 | 36245048832 | 904187206656 | 10165823356160 |
| 5 / 8 | 11631754313984 | 36245048832 | 773752814592 | 10025879203072 |
| 5 / 9 | 11715460088064 | 36245048832 | 651618548736 | 10064307694848 |
| 5 / 10 | 11853464486144 | 36245048832 | 513614150656 | 10064307694848 |
| 5 / Jack | 11987546308864 | 36245048832 | 417960819712 | 10025879203072 |
| 5 / Queen | 11920232497408 | 36245048832 | 345330478080 | 10165823356160 |
| 5 / King | 12115198331136 | 36245048832 | 297628401664 | 10018559598848 |
| 5 / Ace | 15666993755904 | 62122913280 | 321314088960 | 12551073098496 |
| 6 / 6 | 3385436784640 | 2606764032 | 66370031616 | 2679458895872 |
| 6 / 7 | 2948354027520 | 1949847552 | 49832742912 | 2390236164096 |
| 6 / 8 | 2920204382208 | 1949847552 | 39644024832 | 2428574527488 |
| 6 / 9 | 2959320477696 | 1949847552 | 29152235520 | 2399950221312 |
| 6 / 10 | 2961957253120 | 1949847552 | 21267468288 | 2405198213120 |
| 6 / Jack | 2972971364352 | 1949847552 | 15501348864 | 2399950221312 |
| 6 / Queen | 2948350586880 | 1949847552 | 11497820160 | 2428574527488 |
| 6 / King | 2989107425280 | 1949847552 | 9079345152 | 2390236164096 |
| 6 / Ace | 3443969234944 | 2606764032 | 7837581312 | 2679458895872 |
| 7 / 7 | 419126116352 | 35831808 | 863305728 | 323474440192 |
| 7 / 8 | 414744739840 | 35831808 | 661979136 | 328057143296 |
| 7 / 9 | 409041797120 | 35831808 | 460652544 | 333961412608 |
| 7 / 10 | 412687040512 | 35831808 | 309657600 | 330467164160 |
| 7 / Jack | 412800286720 | 35831808 | 196411392 | 330467164160 |
| 7 / Queen | 409390972928 | 35831808 | 111476736 | 333961412608 |
| 7 / King | 415358943232 | 35831808 | 47775744 | 328057143296 |
| 7 / Ace | 419989422080 | 35831808 | 0 | 323474440192 |
Quote: HunterhillSo if you had 9,10,J. You should 4x. What if you saw one of your outs in your neighbors hand or two of of your outs would you still 4x? Would some of the 2x hands become folds?
link to original post
You don't get to draw, so that wouldn't matter much. I suppose if you saw the other players with cards in the middle ranks, it would improve your chances very moderately.
Quote: ThatDonGuyI am getting only 2.77% as the house edge, and I have "raise 2x" on J-10-9
link to original post
I found a bug in my program in scoring wheel hands.
I'll update my page in about an hour, but it looks like the smallest 4x raise should be on 10-J-Q. This gives a house edge of 2.78%, based on a limited simulation. Running a longer one now.
In related news, here is how often I get each high hand.
| Cards in straight | High card | Count |
|---|---|---|
| 7 | A | 16,384 |
| 7 | K | 16,384 |
| 7 | Q | 16,384 |
| 7 | J | 16,384 |
| 7 | 10 | 16,384 |
| 7 | 9 | 16,384 |
| 7 | 8 | 16,384 |
| 7 | 7 | 16,384 |
| 6 | A | 135,168 |
| 6 | K | 118,784 |
| 6 | Q | 118,784 |
| 6 | J | 118,784 |
| 6 | 10 | 118,784 |
| 6 | 9 | 118,784 |
| 6 | 8 | 118,784 |
| 6 | 7 | 118,784 |
| 6 | 6 | 135,168 |
| 5 | A | 630,272 |
| 5 | K | 495,104 |
| 5 | Q | 495,104 |
| 5 | J | 495,104 |
| 5 | 10 | 495,104 |
| 5 | 9 | 495,104 |
| 5 | 8 | 495,104 |
| 5 | 7 | 495,104 |
| 5 | 6 | 495,104 |
| 5 | 5 | 630,272 |
| 4 | A | 2,183,296 |
| 4 | K | 1,553,024 |
| 4 | Q | 1,553,024 |
| 4 | J | 1,553,024 |
| 4 | 10 | 1,553,024 |
| 4 | 9 | 1,553,024 |
| 4 | 8 | 1,553,024 |
| 4 | 7 | 1,553,024 |
| 4 | 6 | 1,553,024 |
| 4 | 5 | 1,553,024 |
| 4 | 4 | 2,166,912 |
| 3 | A | 5,402,496 |
| 3 | K | 3,436,288 |
| 3 | Q | 3,538,688 |
| 3 | J | 3,641,088 |
| 3 | 10 | 3,743,488 |
| 3 | 9 | 3,829,504 |
| 3 | 8 | 3,915,520 |
| 3 | 7 | 4,017,920 |
| 3 | 6 | 4,001,536 |
| 3 | 5 | 3,985,152 |
| 3 | 4 | 3,985,152 |
| 3 | 3 | 4,907,392 |
| All 1 or 2 card straight | 60,598,640 | |
| Total | 133,784,560 |
I actually have studied straights of n-length as a function of number of cards drawn, but I don't think you need my expertise on this one. One interesting nugget is that having a straight in your hand slightly increases the chances of a straight (of equal or greater length) in your opponent's hand. Its because every card in your hand is a straight blocker for specific straights such as 6-2 or K-9, and when you have multiple cards in a row, they all block many of the same potential straights -which is less efficient at blocking straights than having widely spaced ranks.
I'm surprised this game designer didn't allow a discard and draw of, say, 1 or 2 cards to the initial hand. It would have increased the interest level and wagering, but I guess it would have slowed the game and limited the number of players who can be dealt from a 52 card deck.
My page has been updated.
I'm not saying Don is wrong, but I think I'm happy if we agree on the strategy and are within 0.03% on the house edge.
Itís kinda like a community party game. Exciting, and easy to learn. Flamingo hit a home run on this one. Well done!
Quote: BigDaddy316This game is a winner! Fast-paced and fun! We had a blast playing this game at the Flamingo. Hopefully Caesars will expand this to their other properties so the lines to play wonít be so long. And people wonít get up from the table so there was a bit of crowd.
Itís kinda like a community party game. Exciting, and easy to learn. Flamingo hit a home run on this one. Well done!
link to original post
Are you friends with the creator or what? A friend and I didn't experience anything like this when we played this week. We found the game slow and clunky. The card that explained the game described it as exhilarating which we kept making fun of. The table was empty when we approached but after a while a couple joined in to play. The pit and dealers are still new with the game which may have resulted in it playing even slower. The dealer made a number of mistakes. Once a player made a 4x bet and won but the dealer told him he made a mistake, bet too much and made him take some of his bet back. I questioned it, the pit came over and fixed the dealer's error. Following the hand the dealer questioned what a player could bet and the pit clearly said they could bet 2x or 4x and that was it. The actual rules state 2x to 4x.
Anyway, it wasn't a great experience. I may give it one more try. I won't be back in Vegas for several months, if it's still there then I will. Hopefully it will be a smoother experience after that amount of time.
Depending on the game and how much the error in question swings EV, just a dealer committing an error once in a while can sometimes yield a substantial player advantage.
Quote: Mission146If the dealer can make errors one way, then he can make them the other way. Probably something that I would want to observe just to see if any player-benefit errors are common and then try to estimate whether or not that might yield a player advantage based on frequency of errors.
Depending on the game and how much the error in question swings EV, just a dealer committing an error once in a while can sometimes yield a substantial player advantage.
link to original post
I'd say based on the dealer I played with, the player had an advantage provided the players were on their toes and stopped her from making mistakes to their detriment. When the dealer didn't qualify she was paying the play instead of the ante. A significant advantage. There was even discussion over which was correct, she read the information card, and still settled on paying the play being correct. It involved other people being paid so I didn't say a thing in those instances. Even with that it still just wasn't very fun. I also don't like that when dealt correctly only the ante pays when the dealer doesn't qualify. Paying the play and pushing the ante is much better.
1. as others have said, you need to pay the play (2-4x raise) rather than the ante when the dealer doesn't qualify, players hated this when they didn't get the raise payout when the play bet pushed with big straights.
2. the second chance side bet really doesn't look like a progressive on the layout, it plays like one with a low hit rate and players made a lot of bets on it and it never hit in the time I spent, but needs more of an indicator of this rather than the dealer just telling players "it never hits". It also took a while to figure out why the dealer was dealing an extra packet of cards and burning some of them.
Also of note, there are only five player spots available on the game. Not sure why that is when the game could add a sixth player spot with the cards needed (7x7+3)
Quote: mtcards
Also of note, there are only five player spots available on the game. Not sure why that is when the game could add a sixth player spot with the cards needed (7x7+3)
link to original post
With six player spots (filled), you have literally dealt out every card in the 52 card deck. onto the table. I think that most game security experts are uncomfortable with that. They might prefer that the dealer burn the top card, for example.
Fold with 32A or lower
Raise-2 with 432-JT9
Raise-4 with QJT or higher
appears to be basically correct, according to my calculations. However there are exceptions to this strategy. The EV of hands is VERY sensitive to the kickers that you have in your hand, where kickers are defined as the cards that are NOT used to make your straight.
Almost all close decisions involve how to play 3-card straights so we will focus on 3-card straights.
Here are the probabilities I calculate for a 52card deck.
| Straight | Probability |
|---|---|
| AKQ | 0.04537253 |
| KQJ | 0.029787832 |
| QJT | 0.029787832 |
| JT9 | 0.029910298 |
| T98 | 0.029144888 |
| 987 | 0.028501944 |
| 876 | 0.027981465 |
| 765 | 0.027216055 |
| 654 | 0.026052633 |
| 543 | 0.025747426 |
| 432 | 0.025348456 |
| 32A | 0.036195268 |
| DNQ | 0.453718486 |
The probabilities are different for each three card straight. Think of it this as: a hand that is rated as a 987 straight must have a 9-8-7 and no 10s and no 6s, because those cards would make it a straight longer than 3 cards.. It also must not have another three card straight that is higher than 987, nor any 4 card straight. Notice that the frequency of an AKQ straight is quite high, over 4.5%. It has a high probability primarily because there is only one rank -a Jack - that cannot be a kicker -and because whenever the other 4 kickers form a different 3-card straight, the AKQ is always the higher of the two 3-card straights.
In this table, DNQ means Does Not Qualify; it means that the longest straight in your hand is 2 cards or less. The fresh deck (52 cards) value of DNQ is about 45.37% and that is how often you will be dealt a straight no longer then 2 cards. You should fold - except for some extremely rare hands.
You see, the cards in your hand will change the dealer's probability of DNQ. And, when the dealer's DNQ probability exceeds 0.5, the correct play is to Raise-2.
The hands with no 3-card or longer straight that are the most profitable to Raise 2 with are
10-10-10-5-5-5-5
Yep, Tens and Fives: quads of one and Trips of the other.
With these hands, I calculate that the dealer's DNQ is 0.502753439 and the Players EV with Raise-2 = -0.9889862, which is about 1.1 percentage points better than FOLD = -1.0. Of course, these are extremely improbable hands, you could play your whole life and never be dealt either of these 2 hands. But there are other more probable hands that are variations off these hands that are also correct to Raise-2, albeit with less of an EV advantage.
I've also found some other exceptions, some of them non-negligible, in how to play the three-card straight hands. I'll be posting on all of this in the next few days.
First, when you have a 32A straight. The Wizards strategy is fold. I found no exceptions to this strategy. You should always fold, based on the info in your 7-card hand.
The strongest 32A hand I found was: 32A-8888. The eights do a great job of blocking higher 3 card straights as well as straights that are 4-7 in length. Still, the EV I calculate for 32A-8888 is EV = -1.025, which is worse than Folding with an EV of -1.0. So always fold.
432 Straight: Raise-2 or Fold
The WOO strategy is to always Raise-2 on this straight. However, for the extreme case of 432-3222 I calculate a Raise-2 EV= -1.335372134, which is worse than folding by more than 33 percentage points!
To illustrate what is going on with the Raise/Fold decision, I calculated this Effect of Removal chart for removal of single cards from the deck when holding a 432 straight hand.
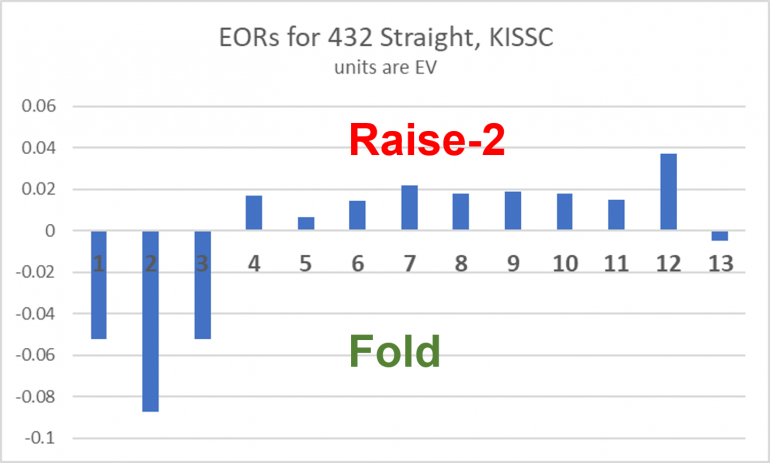
The ranks of the removed card are on the x axis, where 1=Ace, 11=Jack, 12=Queen and 13=King. The y axis is in EV, and yes, the presence of a 2 in your four kickers does lower the EV of a 32A hand by more than 8 percent! The 2 blocks the 32A and 432 straights; i.e., it lowers the probability of the dealer getting a 32A straight in his hand which is the only dealer straight hand that you can win against. It also lowers the probability of the dealer tieing you with a 432.
A 3 amongst your kicker cards reduces the probability of the dealer having a 32A, a 432 and a 543 straight. It's not as disastrous as a 2 but it is bad news. Equally bad news is an Ace in your kicker cards, it blocks the 32A straight that your hand can beat as well as an AKQ straight.
The cards that significantly improve your chances of winning are 6 through 12. A 9 in your kickers blocks the following 3-card straights in the dealer's hand: JT9, T98 and 987 -all straights that you will lose against. A 9 is also efficient at blocking 4-card and longer straights, all of which you will lose against.
So, here's the strategy I recommend when dealt a hand whose best straight is a 432:
Strategy for 432 Straight
Raise-2, except fold when
1. One or more of your four kickers is a 2. (This will occur about 21% of the time.)
2. Your four kickers contain two or more 3s or two or more Aces.
3. Your four kickers contain A3, AK, A4, K3 or 43.
Here is a table of some EV calculations for 432 straights that illustrate the effect of certain cards in the kickers.
| Straight | EV |
|---|---|
| 432-3322 | -1.290633108 |
| 432-3222 | -1.335372134 |
| 432-3328 | -1.224327022 |
| 432-33J8 | -1.108998797 |
| 432-3KJ8 | -1.021663756 |
| 432-2KJ8 | -1.061822928 |
| 432-2J86 | -1.04164982 |
| 432-2J84 | -1.039098653 |
| 432-3J84 | -1.010855402 |
| 432-3AJ8 | -1.062290429 |
| 432-3J86 | -0.996363676 |
| 432-3KJ7 | -1.023037765 |
| 432-33J6 | -1.05452062 |
| 432-AAJ7 | -1.0277659 |
| 432-AKT6 | -1.027806359 |
| 432-AT64 | -1.008769312 |
| 432-2888 | -0.988887016 |
| 432-2J88 | -1.012819874 |
| 432-2Q88 | -0.998284715 |
| 432-3K88 | -0.972368764 |
The last four rows in the table show that my proposed strategy does not always work when there are 88 pairs or 888 trips in the kickers. Mid-rank cards such as 7,8, or 9 are very effective at blocking straights, and a pair or trips of these cards are very efficient at blocking straights because multiple cards of the same rank do not interfere with each other when blocking straights. By this I mean that an 888 will reduce the probability of dealer straights more efficiently than a 789.
So, the strategy I propose for the 432 Fold/Raise-2 decision could be improved by adding exceptions to the exceptions so as to account for this circumstance, but at the expense of complicating the strategy.
The EV of a 543 straight without any kickers (a 3-xard hand) in KISSC is EV = -0.813431757, which is well below -1.0, so that why you generally want to Raise-2 with this hand. However, let's look at the EOR on the EV of a 543 straight.
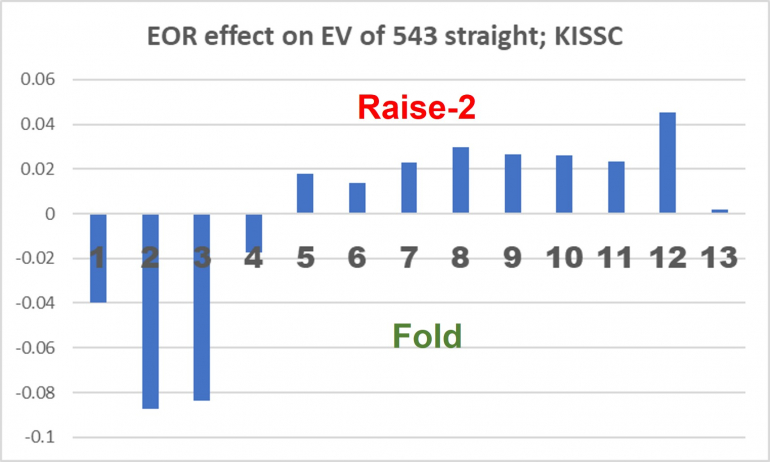 .
.The Effect of Removal for a 2 or 3 is huge: ΔEV > -0.083 (note I've included 2 and 6 in this chart, even though they are defined to not be in a 543 hand, because they could be in your neighbor's hand.) That's easy to understand. The only dealer 3-card straights that a 543 can beat are 32A and 432; and the removal of a 3 or a 2 from the deck will reduce the probability of both the 32A and 432 straights from occurring. Ace is also a card whose removal hurts the EV of a 543 straight, primarily because it blocks the 32A straight from occurring in dealer's hand
The hand 543-3334 is the worst possible variant of a 543 hand that player can hold; it has an EV = -1.12555. Note that with all four 3s in the deck you have completely eliminated any chance of the dealer have a 32A or 432 straight, and thus you only avoid losing when the dealer's hand Does Not Qualify (with maximum straight length of 2 or 1.) In this circumstance the addition of an Ace in this hand is superfluous in lowering EV because the 32A straight already has no chance of occurring, so the 4 becomes the worst card to add to a 543-3333 hand.
The strategy for a 543 hand is:
With 543 straight: Raise-2 except Fold when
1. Your kickers have three 3s; i.e. you hand has all fours threes.
2. Your kickers have two 3s, and your other 2 kickers are
a) A-x where x is any card except an 8 or a Q, or
b) K-4 or 6-4
These exceptions will occur very infrequently in player's hand, so as a practical manner this perfect strategy is a negligible improvement over "Always Raise-2 with 543 straight."
JT9 Strategy
With a JT9 3-card straight, you should Raise-2 except Raise 4 when the four kickers are:
a) K-K-Kx or J-J-Jx (including K-K-K-K and J-J-J-K)
b) K-J-J-x or K-K-J-x when x >3
b) K-K-T-T
When you have a JTP 3-card straight and use this strategy, you will only Raise-4 a bit more frequently than 1% of the time.
QJT Strategy
With a QJP 3-card straight, you should Raise 4 except Raise-2 when:
a) the four kickers are all of the ranks 2 -8, T, or A; and when at least two of the kickers are some combination of 2s and 3s. Example: Raise-2 with QJ9-3285.
i) exception to this exception: Raise-4 with QJT-22AA and QJT-33AA
b) Also, Raise-2 when the four kickers are exactly 3-3-3-J and 2-2-2-J
c) Also, Raise-2 when the four kickers are exactly 3-T-T-T or 2-T-T-T
The main idea is that the presence of cards with ranks 2-8,10 and Ace all reduce the probability of dealer getting a 3-card straight hand in the range 32A-JT9 - which are the straights that your QJT hand can beat. Thus, you will tend towards choosing Raise-2 when these lower straights become significantly less likely.
Below I am presenting the frequency of 7 card hands in which the longest straight is n cards and n varies from 1 to 7. I think this is a novel calculation, in any case I personally have never seen the one-card straight value published.
| Longest Straight | Probability |
|---|---|
| 7 | 0.00098 |
| 6 | 0.00824 |
| 5 | 0.03903 |
| 4 | 0.13638 |
| 3 | 0.36166 |
| 2 | 0.41481 |
| 1 | 0.03891 |
To be clear, a 1-card straight is a hand that has no adjacent ranks in it. Note that all of the so-called 1- card straights have at least one pair in them. Even the hand A-Q-10-8-6-4-2 has a two card straight: 2A. An example of a legitimate 1-card straight hand is: KK-J-77-4-2.
Why are 1-card straights relevant to this conversation? Well, because 1-card straight hands are virtually the only hands which have some chance of causing the dealerís DNQ probability to rise above 0.5 and thus shift the optimal strategy decision from FOLD to Raise-2. Whenever you have a hand whose longest straight is two cards, you should automatically fold (two minor exceptions, below). But when you are dealt a hand with no adjacent ranks in it, you should stop and at least consider whether it should be Raised with a 2-unit bet.
In a previous post, I said that 10-10-10-10-5-5-5 and 5-5-5-5-10-10-10 were the only two hands (with no straights longer than 2 cards) that blocked enough dealer straights that they should be Raised rather than folded. I was thoroughly wrong, as I have come to realize. There are many 1-card straight hands that should be Raised. It is an interesting subject.
The best 1-card straight hand that I have found is QQQQ-999. When Raise-2, this hand has an EV = -0.827539, which is more than 17 percentage points better than Fold EV = -1.0!
Preliminary strategy: FOLD/Raise-2 decision on hands whose longest straight is less than 3-cards in length.
Always Fold a hand whose longest straight is exactly 2 cards in length, there are a few minor exceptions listed below.
For hands with no adjacent ranks, i.e., whose longest straight is exactly 1 card in length, you should generally fold. However, there are exceptions:
1. Raise-2 with any hand in which all 7 cards are, in any combination, a 3,6,9, or Q. Example: Raise-2 with Q-99-66-33.
2. Raise-2 with any hand that has Quads of one rank and 3-of-a-kind of another rank if both ranks are in the range 3-Q and there are at least two gaps between the ranks.
3. Raise-2 with any hand that has quads of one rank, a pair of a 2nd rank and a singleton in a third rank that meets the following conditions:
___a. All cards are in the range 3-Q
___b. The quads and pair are separated in rank by exactly 2 gaps
___c. The rank of the singleton is not adjacent to the ranks of either the quads or pair. (remember, this must be a 1-card straight hand, which means no adjacent ranks.)
4. Raise-2 with any hand that has two 3-of-a-kinds (of different ranks, obviously) and a singleton in a third rank that meets the following conditions:
___a. All cards are in the range 3-Q
___b. The two 3-of-a-kinds are separated in rank by exactly 2 gaps
___c. The rank of the singleton is not adjacent to the ranks of either of the ranks of the two 3-of-a-kinds.
5. This exception addresses hands with one 3oaK, one pair and two singletons that are not entirely comprised of 3,6,9 and Q.
___a. When your hand is exactly 333-66-9-X or 333-99-6-X you should raise-2 when X is a 7,8,10, J, or K. Note that when X =7,8 or 10 it is forming a two-card straight, so this is the extremely rare exception where a hand with two adjacent ranks should be raised.
___b. When your hand is exactly QQQ-99-6-X or QQQ-66-9-X you should raise-2 when X is a 2,4,5,7,8. Note that when X =5,7, or 8 that this hand is also forming a two-card straight, so this is another extremely rare exception to the general rule.
Notes:
1. This strategy is probably not perfect, as there are probably a few ďno-straightĒ hands that I have missed with an EV just a tad lower than (-1.0). Still I think this has scooped up most of the EV that one can achieve by Raising hands with no 3-card or longer straights.
2. These rules may seem complicated, but they make a certain kind of sense. For example, the ranks 2,K and A are usually excluded from most of these rules because these ranks are relatively inefficient at blocking 3 -card straights and even less efficient (relative to other ranks) at blocking 4-card and longer straights.
3. Regarding the first rule for exceptions, hands where all 7 cards are either a 3,6,9, or Q: I have calculated that this category of hands occurs with a frequency of 0.0000789 and collectively will lower the house edge by 0.00000458 or 0.000458%. So, this exception, and all the others, I presume, have a negligibly small impact on the bottom line. But some of us are obsessive about striving for every increment of expected value that we can get. And I think its of value that some poor wretch somewhere has evaluated a more rigorous strategy. If for no other reason that to assure ourselves that we are not missing something. Because . . .
4. As a matter of fact, we have indeed missed something. Something entirely new, I think, and of possible significance. You see, I stumbled onto something and havenít really mentioned it yet. Iíll plan to discuss it in my next post - while being mindful of the limits being placed on us by the forum rules.
The magical thing about these four ranks, is that if all 16 cards of these four ranks are removed from the deck then the dealer will have zero probability of making a straight that is 3-cards or longer in length. That's correct: Zero probability. Dealer has 100% probability of not qualifying. No other combination of ranks can achieve 100% DNQ with less than 20 cards.
In this game the player will be folding his hand almost 50% of the time. Clearly if you knew that the dealer had little to no chance of qualifying, you would at least Raise-2 on every hand and take the +1 unit payout from the Ante Wager when dealer has a DNQ.
So what if an AP team filled the 5 seats and simply counted the number of 3s, 6s, 9s and Qs in their hands, and signaled the information, and acted accordingly? After all, 5 players have 35 cards in their hand.
In the table below, I show some results for those occasions when the five players have 13 to 16 of the 369Q cards in their hands. The first column is the number of those 369Q cards that they count in their hands, the 2nd column is the frequency with which that will happen. The 3rd and 4th column are my estimated average values of DNQ and EV that they can achieve and the last column is probability*ΔEV or the reduction in the House Edge achievable for that specific count..
| Count of 369Q cards | Probability | Dealer DNQ | Approx EV | ΔReturn |
|---|---|---|---|---|
| 16 | 0.000392 | 1 | 1 | 0.000403 |
| 15 | 0.005328 | 0.75 | 0.4 | 0.002428 |
| 14 | 0.030446 | 0.5675 | 0.116 | 0.004389 |
| 13 | 0.096873 | 0.49 | -0.028 | n.a. |
Well, this is not a viable collusion method. If you have exactly 13 cards in the 369Q quartet, it appears that the DNQ is about 0.49 and with DNQ<0.5 the players have no basis for gaining an advantage by Raising every hand. And by raising every hand when you have 14, 15 or 16 cards I estimate that you can only lower the HE by a total of 0.7% (the sum of the last column). The values of DNQ and EV in my table are not exact but they should be in the ballpark; however, the values of probability should be exact -and it is these low probabilities of occurrence that make this an unattractive method for collusion. And no 5-man team is going to count cards to lower the HE from 2.8% to 2.1%.
I did some quick calculations for 6 players and 42 cards -and that is a different story. The game might indeed be vulnerable to collusion by this method with 42 cards to work with. That is probably why there are only 5 seats at the KISSC table.


