I'm calling out the Discovery Channel and Andy Bloch
Poll
 | 2 votes (7.69%) | ||
| No votes (0%) | |||
| | 2 votes (7.69%) | ||
| | 4 votes (15.38%) | ||
| | 4 votes (15.38%) | ||
| | 5 votes (19.23%) | ||
| | 3 votes (11.53%) | ||
| | 6 votes (23.07%) |
26 members have voted
September 15th, 2014 at 8:37:10 AM
permalink
but is as gentle as a puppyQuote: WizardHmmmm. This gigantic matrix sounds intimidating.
It is easy to populate the probs too with 1 if statement filled across and down for each block that does the same thing
>=500 is just bank-(target-bank)once at 975 the bankrolls can only be
and below 500 one must win
spin bank bet
1 975 25
2 950 50
3 900 100
4 800 200
5 600 400
6 200 200
7 400 400
8 800 200
9 600 400
10 200 200
11 400 400
12 800 200
13 600 400
14 200 200 etc
I now work on how entering the bold play from 3 after the first loss
it is currently
spin bank bet won
1 3 3 105
2 108 26 910
3 82 27 945
4 55 27 945
5 28 28 980
because the above bold play over-shoots the target, we can do better at spins 2:5
by lowering the bet by 1
once that is done then I can get the best prob from that method and copy/paste another worksheet and enter your transition probs
the bark sound way worse than the bite
Sally
I will do my best to clean up my worksheet and can upload it later too
I Heart Vi Hart
September 15th, 2014 at 10:50:49 AM
permalink
Quote: mustangsallyI will do my best to clean up my worksheet and can upload it later too
Thanks. I would appreciate that.
After doing a bigger simulation my latest Wizard strategy is at 2.8068%.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
September 15th, 2014 at 11:27:43 AM
permalink
I rewrote my strategy for about the 8th time, somewhat based on what I understand of your strategy, and it is coming in around 2.808%. I'll let the simulation run for three hours to get a more accurate figure.
I'm still eager to see your spreadsheet. One bet I have a hard time agreeing with is betting 400 with a bankroll of 400, which I presume is on an even money bet. My strategy would bet 300 on any column. Then again, maybe betting $17 on a single number is right, but I wasn't getting good returns with betting single numbers with a large bankroll.
I'm still eager to see your spreadsheet. One bet I have a hard time agreeing with is betting 400 with a bankroll of 400, which I presume is on an even money bet. My strategy would bet 300 on any column. Then again, maybe betting $17 on a single number is right, but I wasn't getting good returns with betting single numbers with a large bankroll.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
September 15th, 2014 at 11:33:34 AM
permalink
Sally likes to copy and paste (because I am good at it)Quote: WizardThanks. I would appreciate that.
After doing a bigger simulation my latest Wizard strategy is at 2.8068%.
and sometimes that causes problems from one spreadsheet to another as a cell could be formatted as text in one but I want general in another
I can not at this point in time make my simple Excel Bold Play sheet match my simple excel 1001x1001 matrix
12 out of 13 values match
ugh
I might have to start over for the matrix (no big deal really)
I know the Excel BP sheet is perfect as it always matches BruceZ's code he made for me
I want to finish first my Banker Baccarat Bold Play sheet, almost done with 19/20 payoff, to match the code of this
> p <- pdoubb(30,1000,500,0.50682483,19/20,0.0000000001)
> p
[1] 0.02807831
that will make me feel better
Sally
I Heart Vi Hart
September 15th, 2014 at 11:37:03 AM
permalink
It is a starting point.Quote: WizardOne bet I have a hard time agreeing with is betting 400 with a bankroll of 400, which I presume is on an even money bet.
the matrix calculates this almost instantly for any change made
I just have to get back to it
as I explained in the last post it is not 100% correct and I can not find the problem
Sally
I Heart Vi Hart
September 15th, 2014 at 12:37:27 PM
permalink
me tooQuote: WizardI'm still eager to see your spreadsheet.
problem solved, Sally is back on the train
My husband asked me if the two values were close enough that maybe one was not calculated right.
I know the matrix = 0.028029406 (I did it 3 different ways and the value was the same each way)
(this is the $27 su to 950 and even money to 1000 = (1/38)*P1 +
$3 if that fails and su to 1000+) (37/38)*P2
of course my error was right there (37/38)*P2 as I only had P2
the 15x15 matrix
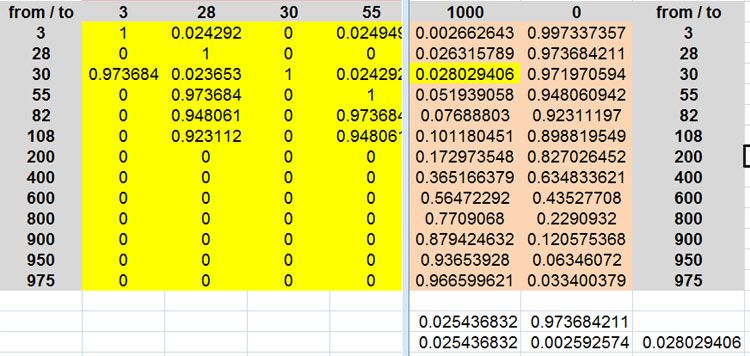
Ohhhhhhhhhhhhhhhhhhhhhhhhhh such a simple mistake and a waste of an hour for me finding it
Okay, Sally ain'ts perfect, see
now I know me matrix is right and I can set up your trans probs
because after reading about "How to Gamble if you Must"
for any starting bankroll as a fraction of the target, there does exist at least one optimal solution,
many times many of them
Lunch time and maybe a nap too
Sally tired again!
I Heart Vi Hart
September 15th, 2014 at 6:01:36 PM
permalink
Thanks Sally for all your hard work on this. Does this mean that you've revised your probability of turning 30 into 1000 to 2.8029406%?
I've gotten as high as 2.8074% with this strategy:
With less than $35 to go, bet the lesser of your goal and your bankroll.
With more than $35 to go, bet as much as you can on a single number, without going over the goal if you win.
I've gotten as high as 2.8074% with this strategy:
With less than $35 to go, bet the lesser of your goal and your bankroll.
With more than $35 to go, bet as much as you can on a single number, without going over the goal if you win.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
September 15th, 2014 at 6:16:02 PM
permalink
It was time for me to update my worksheetsQuote: WizardThanks Sally for all your hard work on this.
Does this mean that you've revised your probability of turning 30 into 1000 to 2.8029406%?
that is correct as I stated it
But I know it can be better, how much no know yet,
than that because 3 out if the 4 bets go over 1000 and that takes away points
after dinner I want to play with that
I was waiting too to see if you posted your strategy so I can enter them into the matrix
so you have a different one below
in Excel the file is 17MB in .xlsb (2007)
to make it work faster I always go into the registry and set the undo to 0
that really speeds up the many calculations going on
just have to make sure to not make a large mistake
I do not get this, but it is dinner timeQuote: WizardI've gotten as high as 2.8074% with this strategy:
With less than $35 to go, bet the lesser of your goal and your bankroll.
this seems rightQuote: WizardWith more than $35 to go, bet as much as you can on a single number, without going over the goal if you win.
Sally
added: If you go to my blog
there is a link to onedrive
many excel files i have there
look or download the
roul-15x15 - Copy.xlsb file
to see my ver1 matrix and how I solve this
now for dinner and a movie
Sally
I Heart Vi Hart
September 16th, 2014 at 8:59:26 AM
permalink
what I think you mean is needing 34 or less, make an even money betQuote: WizardI've gotten as high as 2.8074% with this strategy:
With less than $35 to go, bet the lesser of your goal and your bankroll.
With more than $35 to go, bet as much as you can on a single number, without going over the goal if you win.
needing 35 or more, a one-number bet, not to go over 1000
with the conditions I spelled out
I gets = 0.028062298
when I change it to a bankroll of 900 or more, bet bold on even money
and <899 just one-number
0.028073638
when I change it to a bankroll of 500 or more, bet bold on even money
and <500 just one-number
0.028060116
that looks to have made it worse
looks like room for improvement
now to clean up my sheet and upload it to my online folder
That will have to be later today
Sally
I Heart Vi Hart
September 16th, 2014 at 9:14:28 AM
permalink
Quote: wudgedSingle or double zero?Quote: WizardTrivia time! What is the sum of all the numbers on a roulette wheel?
now that there is funny!
the next time Dame Fortune toys with your heart, your soul and your wallet, raise your glass and praise her thus: “Thanks for nothing, you cold-hearted, evil, damnable, nefarious, low-life, malicious monster from Hell!” She is, after all, stone deaf. ... Arnold Snyder
September 16th, 2014 at 10:04:48 AM
permalink
Here is a preview of a my future Ask the Wizard question on this topic. I welcome all comments.
No, he's not.
The probability of Andy's single bet strategy is 1/38 = 2.6316%.
First, it isn't difficult to see that the odds are better by betting $28 on a single number, which would get you to $1,010 if you win. If you lose, you still have $2 left, which has a 0.1774% chance of being parlayed into $1,000 with my Wizard's "Quick Score" roulette strategy" below. Considering this $2 second chance, the probability of reaching $1,000 goes up to 2.8090%.
However, betting $28 on a single number will cause you to overshoot the goal by $10 if you win on the first bet. If you instead bet $27 on a single number and then go into my "Quick Score" roulette, win or lose, the probability of turning $30 into $1,000 goes up to 2.8074%.
What about other games, you might ask? According to the Discovery Channel voice-over guy, "Everyone agrees that roulette is the best get rich quick scheme in the casino." Well, I don't. Even limiting ourselves to common games and rules, I find craps to be better. In particular, betting the don't pass and laying the odds.
Following my Quick Score strategy for craps (explained below) the probability of turning $30 into $1,000 is 2.9244%. This assumes the player may lay 6x odds, regardless of the point (which is the case when 3x-4x-5x odds are allowed taking the odds). This probability of success is 0.1173% higher than my Quick Score strategy for roulette, and 0.2928% higher than the Andy Bloch strategy.
In all fairness, Andy could argue that my strategy entails betting as little as $1 in craps and roulette, when most casinos have higher minimums than that. My counter argument would be that minimums were never mentioned on the show, and that one can evade minimum bet rules by piggybacking on somebody else's bet. Nevertheless, if we assume a $5 minimum bet rule, then Andy would probably be right.
Wizard's Quick Score strategy for roulette.
This strategy assumes that bets must be in increments of $1. In all bet calculations, round down.
Let:
b = Your bankroll
g = Your goal
1. If (g-b)>=35 then make then bet min(b,int((g-b)/35) on any single number. In other words, make the largest bet you can afford on a single number that won't cause you to overshoot your goal.
2. Otherwise, if you're within $34 of your goal, bet g-b on any even money bet.
Wizard's Quick Score strategy for craps.
This strategy assumes that bets must be in increments of $1 and wins will be rounded down to the nearest dollar. In calculating bets, never bet so much that you overshoot the goal. Also, never make a bet amount that will cause you to get rounded down.
Let:
b = Your bankroll
g = Your goal
1. Bet max($1,min(b/7,(g-b)/6)) on the don't pass.
2. If a point is rolled, and you have enough for a full odds bet, then lay the full odds. Otherwise, lay whatever you can.
So, I hope Andy and the Discovery Channel are happy. I've spent days running simulations to prove them wrong.
Quote: QuestionThe Hustling House show on the Discovery Channel had a long segment on the best way to turn $30 into $1,000. It featured Andy Bloch saying, "If you have $30 in your pocket and you want to turn it into $1,000 then roulette is your only game." Andy went onto explain why betting the whole $30 on a single number was better than parlaying even money bets five times.
Is Andy correct in that the best way to turn $30 into $1,000 is to put the whole $30 on a single number in roulette?
No, he's not.
The probability of Andy's single bet strategy is 1/38 = 2.6316%.
First, it isn't difficult to see that the odds are better by betting $28 on a single number, which would get you to $1,010 if you win. If you lose, you still have $2 left, which has a 0.1774% chance of being parlayed into $1,000 with my Wizard's "Quick Score" roulette strategy" below. Considering this $2 second chance, the probability of reaching $1,000 goes up to 2.8090%.
However, betting $28 on a single number will cause you to overshoot the goal by $10 if you win on the first bet. If you instead bet $27 on a single number and then go into my "Quick Score" roulette, win or lose, the probability of turning $30 into $1,000 goes up to 2.8074%.
What about other games, you might ask? According to the Discovery Channel voice-over guy, "Everyone agrees that roulette is the best get rich quick scheme in the casino." Well, I don't. Even limiting ourselves to common games and rules, I find craps to be better. In particular, betting the don't pass and laying the odds.
Following my Quick Score strategy for craps (explained below) the probability of turning $30 into $1,000 is 2.9244%. This assumes the player may lay 6x odds, regardless of the point (which is the case when 3x-4x-5x odds are allowed taking the odds). This probability of success is 0.1173% higher than my Quick Score strategy for roulette, and 0.2928% higher than the Andy Bloch strategy.
In all fairness, Andy could argue that my strategy entails betting as little as $1 in craps and roulette, when most casinos have higher minimums than that. My counter argument would be that minimums were never mentioned on the show, and that one can evade minimum bet rules by piggybacking on somebody else's bet. Nevertheless, if we assume a $5 minimum bet rule, then Andy would probably be right.
Wizard's Quick Score strategy for roulette.
This strategy assumes that bets must be in increments of $1. In all bet calculations, round down.
Let:
b = Your bankroll
g = Your goal
1. If (g-b)>=35 then make then bet min(b,int((g-b)/35) on any single number. In other words, make the largest bet you can afford on a single number that won't cause you to overshoot your goal.
2. Otherwise, if you're within $34 of your goal, bet g-b on any even money bet.
Wizard's Quick Score strategy for craps.
This strategy assumes that bets must be in increments of $1 and wins will be rounded down to the nearest dollar. In calculating bets, never bet so much that you overshoot the goal. Also, never make a bet amount that will cause you to get rounded down.
Let:
b = Your bankroll
g = Your goal
1. Bet max($1,min(b/7,(g-b)/6)) on the don't pass.
2. If a point is rolled, and you have enough for a full odds bet, then lay the full odds. Otherwise, lay whatever you can.
So, I hope Andy and the Discovery Channel are happy. I've spent days running simulations to prove them wrong.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
September 16th, 2014 at 10:32:02 AM
permalink
Quote: WizardHere is a preview of a my future Ask the Wizard question on this topic. I welcome all comments.
Quote: QuestionThe Hustling House show on the Discovery Channel....
Is it "The Hustling House" or "Beating the House" as you said in post #1 of the thread? I have never watched it.
September 16th, 2014 at 10:48:52 AM
permalink
It should be the best way to turn $30 into zero.
I would take a challenge(for enough money). I could turn 30 into $100 3 months in a row.
I would take a challenge(for enough money). I could turn 30 into $100 3 months in a row.
♪♪Now you swear and kick and beg us That you're not a gamblin' man Then you find you're back in Vegas With a handle in your hand♪♪ Your black cards can make you money So you hide them when you're able In the land of casinos and money You must put them on the table♪♪ You go back Jack do it again roulette wheels turinin' 'round and 'round♪♪ You go back Jack do it again♪♪
September 16th, 2014 at 11:27:56 AM
permalink
Andy is always happyQuote: WizardSo, I hope Andy and the Discovery Channel are happy.
he does come from yellow submarine land! (I mean close, how many know what that means?)
now he must be even happier
I means
he has a law degree (from where?) and is a poker player and a blackjack player, all +EV
(maybe even more)
so he must know some stuff well, or very very well
not to mention his electrical engineering degree(s) (from where?)
I would like to see Andy and Mike arm wrestle for (?)
best out of 3
oh, now to see if Baccarat Banker beats Andy too, I think it will...
my Excel getting a nice workout
R just yawns
Sally
I Heart Vi Hart
September 16th, 2014 at 11:31:42 AM
permalink
(formatting added)Quote: Wizard
First, it isn't difficult to see that the odds are better by betting $28 on a single number, which would get you to $1,010 if you win. If you lose, you still have $2 left, which has a 0.1774% chance of being parlayed into $1,000 with my Wizard's "Quick Score" roulette strategy" below. Considering this $2 second chance, the probability of reaching $1,000 goes up to 2.8090%.
However, betting $28 on a single number will cause you to overshoot the goal by $10 if you win on the first bet. If you instead bet $27 on a single number and then go into my "Quick Score" roulette, win or lose, the probability of turning $30 into $1,000 goes up to 2.8074%.
Wiz, is that 1st number supposed to be 2.8029 (from your post on pg 6)?
"Dealer has 'rock'... Pay 'paper!'"
September 16th, 2014 at 12:00:57 PM
permalink
a real gambler would borrow a gun for $30 and follow a winner into the parking lot.
Shed not for her
the bitter tear
Nor give the heart
to vain regret
Tis but the casket
that lies here,
The gem that filled it
Sparkles yet
September 16th, 2014 at 12:11:40 PM
permalink
and beyondQuote: Buzzarda real gambler would borrow a gun for $30 and follow a winner into the parking lot.
yes, they are common here in SoCal
but they do have their own gun (from where?)
they fear no one,
a real gambler that is
Sally
I Heart Vi Hart
September 16th, 2014 at 6:15:59 PM
permalink
################################
# The Hustling House show on the Discovery Channel had a long segment on the best way to turn $30 into $1,000.
# It featured Andy Bloch saying,
# "If you have $30 in your pocket and you want to turn it into $1,000 then roulette is your only game."
# Andy went onto explain why betting the whole $30 on a single number was better than parlaying even money bets five times.
################################
I want to now watch that show
I still love Andy!
He is right if comparing just the game of Roulette
Now I have to watch that show
=========================
00 Roulette all $30 one spin = 2.6315789%
0 Roulette all $30 one spin = 2.7027027%
even money bets
Bold Play Player bet in Baccarat
2.7925413%
added:9/16
Bold Play Banker bet in EZ Baccarat (no commission - push Banker win 3 card total of 7)
2.8242171% <<<sweet
5% Banker Baccarat = 2.816% (first 20 bets)
nice but the bets have to be calculated after each round of play
(2*bank<=500 or roundup(1000-bank/0.95))
with bets of for Player bet only
pass line (another even money bet)
2.7852831%
don't pass
2.7869856%
same bets as with Player in Baccarat
looks like many even money bets beats the one number roulette bet method
============================
18/37 Roulette = 0.02600304
18/38 Roulette = 0.022613824
Maybe Andy only did that math first in his head
Was Andy bluffing?
could you tell?
Sally
more movies too
# The Hustling House show on the Discovery Channel had a long segment on the best way to turn $30 into $1,000.
# It featured Andy Bloch saying,
# "If you have $30 in your pocket and you want to turn it into $1,000 then roulette is your only game."
# Andy went onto explain why betting the whole $30 on a single number was better than parlaying even money bets five times.
################################
I want to now watch that show
I still love Andy!
He is right if comparing just the game of Roulette
Now I have to watch that show
=========================
00 Roulette all $30 one spin = 2.6315789%
0 Roulette all $30 one spin = 2.7027027%
even money bets
Bold Play Player bet in Baccarat
2.7925413%
added:9/16
Bold Play Banker bet in EZ Baccarat (no commission - push Banker win 3 card total of 7)
2.8242171% <<<sweet
5% Banker Baccarat = 2.816% (first 20 bets)
nice but the bets have to be calculated after each round of play
(2*bank<=500 or roundup(1000-bank/0.95))
with bets of for Player bet only
30
60
120
240
480 <<<5th win in a row right there
40
80
160
320
360
280
440
120
240
480
40 etc
pass line (another even money bet)
2.7852831%
don't pass
2.7869856%
same bets as with Player in Baccarat
looks like many even money bets beats the one number roulette bet method
============================
18/37 Roulette = 0.02600304
18/38 Roulette = 0.022613824
Maybe Andy only did that math first in his head
Was Andy bluffing?
could you tell?
Sally
more movies too
I Heart Vi Hart
September 25th, 2014 at 8:48:15 AM
permalink
I missed thisQuote: WizardThe probability of Andy's single bet strategy is 1/38 = 2.6316%.
In all fairness, Andy could argue that my strategy entails betting as little as $1 in craps and roulette, <snip> <snip>
Nevertheless, if we assume a $5 minimum bet rule, then Andy would probably be right,
the answer is to "probably be right"
Quote: Wizard<snip> wrong.
I showed in my last post here the even money bets made for pass,
don't pass and Baccarat Player bets,
as well as the Baccarat Banker bets, both with 5% comm and EZ Bac,
and all of them beat Andy with proper $5 unit bets
(beats Andy at 1/38 or 1/37)
final answer,
Andy was wrong (by that much)
according to what you claimed he said
as I still have not heard his exact comments
Sally
I Heart Vi Hart
