Poll
 | 2 votes (7.69%) | ||
| No votes (0%) | |||
 | 2 votes (7.69%) | ||
 | 4 votes (15.38%) | ||
 | 4 votes (15.38%) | ||
 | 5 votes (19.23%) | ||
 | 3 votes (11.53%) | ||
 | 6 votes (23.07%) |
26 members have voted
The probability of success with that strategy is 1/38=2.63%.
An obviously superior strategy would be to bet just $27 on a single number. If you win, you'll be at $975. If you lose you'll be at $3. Either way, make the smallest bet possible that will put you at exactly $1000 on any of the available bets, or your full bankroll if you don't have enough to reach $1000 in one bet. If such optimal bet is not an integer, then round down. Keep repeating until you get to $1000 or $0. I find the probability of success is 2.81%.
However, an even better strategy of betting 1/6 of your bankroll on the pass line in craps, followed by max odds (assume 3-4-5x allowed). If this would put you over $1,000 or cause a bet that isn't evenly divisible by $1, or cause a win that isn't divisible by $1, then round the bet down. I find such a strategy has a probability of success of 2.91%.
I'm going to look at the don't pass plus laying odds next.
The question for the poll is what would be your first bet if the goal was to maximize your chance of turning $30 into $1000? Let's assume the standard casino games available in any medium-sized casino.
Quote: Wizard...The question for the poll is what would be your first bet if the goal was to maximize your chance of turning $30 into $1000? Let's assume the standard casino games available in any medium-sized casino.
How about Craps? Hop a pair for the first leg, then go don't pass/lay odds for the balance?
Quote: WizardThe question for the poll is what would be your first bet if the goal was to maximize your chance of turning $30 into $1000? Let's assume the standard casino games available in any medium-sized casino.
Video poker might be worth looking into. A royal at 25c denom conveniently pays $1000. The problem becomes one of semantics -- which video poker paytables can we use? 100%+ games are not uncommon at quarter denom.
It's also not clear if playing games that require actual skill violates the spirit of the question.
Quote: AyecarumbaHow about Craps? Hop a pair for the first leg, then go don't pass/lay odds for the balance?
The "first leg" only wins 2.78% of the time. That means that you succeed strictly less often than that.
This strategy only really requires three or four sevens as opposed to six passes unless I am missing something. Of course, you could get picked off, but not all on the same roll.
Quote: IbeatyouracesOne other reason Andy is wrong as well is that he should have said SINGLE zero roulette.
Not easy to find with a $30 bet.
Quote: BozNot easy to find with a $30 bet.
I can name six places on the Strip that have $25 min Single Zero during the day. Four of them have European rules. There are probably more MGMs that have them in high limit that will open upon demand.
Played $40 yesterday on roulette losing but close(#30 not #9), then won $250 from a $20 buy in. Was absolutely wasted and even accidentally bet the first ten on the pass line after the point was made. 7 out the first throw and was shocked I lost.
A few 7-11s, doubling pass line wagers, then $10 pass lines minimum with odds on 4 to get into comfort. Skipped one odds on 6 point bet early because the dice landed 45° angle against the wall-voodoo maybe thinking 6 wasn't supposed to be the number. Nothing happened too much in succession though.
I was the hot shooter for 20-30 minutes though, so the probability was probably about 40%. Lol
The most I took was 5x odds by the way.
Somehow say you go $200 to $7000, I don't want to hold so much as $3200 and even risk it to get there.
Quote: WizardEarlier this week there was a show on the Discovery Channel called Beating the House. Part of the show featured Andy Bloch making the claim that the best way to turn $30 into $1000 was to bet the full $30 on a single number in double-zero roulette.
The probability of success with that strategy is 1/38=2.63%.
An obviously superior strategy would be to bet just $27 on a single number. If you win, you'll be at $975. If you lose you'll be at $3. Either way, make the smallest bet possible that will put you at exactly $1000 on any of the available bets, or your full bankroll if you don't have enough to reach $1000 in one bet. If such optimal bet is not an integer, then round down. Keep repeating until you get to $1000 or $0. I find the probability of success is 2.81%.
However, an even better strategy of betting 1/6 of your bankroll on the pass line in craps, followed by max odds (assume 3-4-5x allowed). If this would put you over $1,000 or cause a bet that isn't evenly divisible by $1, or cause a win that isn't divisible by $1, then round the bet down. I find such a strategy has a probability of success of 2.91%.
I'm going to look at the don't pass plus laying odds next.
The question for the poll is what would be your first bet if the goal was to maximize your chance of turning $30 into $1000? Let's assume the standard casino games available in any medium-sized casino.
Vegas 2047 will allow you to bet $30 to win $1000 in a single bet. Our entire mission is GIVING ALL PLAYERS THE BEST POSSIBLE CHANCE TO WIN.
I just did a don't pass plus odds simulation and the probability of reaching the $1,000 goal using the same kind of grinding technique, careful to never exceed the goal or lose anything to rounding, is 2.92%.

Quote: WizardEarlier this week there was a show on the Discovery Channel called Beating the House. Part of the show featured Andy Bloch making the claim that the best way to turn $30 into $1000 was to bet the full $30 on a single number in double-zero roulette.
The probability of success with that strategy is 1/38=2.63%.
I don't necessarily know what the best strategy is, but I can do better than this Andy Bloch without even thinking about it very hard.
First off, take the full $30 and Reverse-Martingale at Craps, five wins in a row goes ($60-$120-$240-$480-$960) and has probability:
(.4929)^5 = 0.02909337405
At this point, you need $40 to reach a total of $1,000, so you're going to Martingale as follows:
$40 ($920 left), $80 ($840 left), $160 ($680 left), $320 ($360 left).
Okay, so you take the probability of initial success of 0.02909337405 and then you only have to win one out of four to be at exactly $1,000, and the probability of losing four in a row is:
(.5071)^4 = 0.06612633336
Now, you have $360 left, so really you should bet it all to $720 and then bet $280, but all of those possibilities are going to take half of forever, so I'm just going to go for two wins in a row and not be heart-broken by the fact that I have $1440 instead of $1,000, if successful.
Okay, so the ways for me to lose after getting to the $960 are to either lose five in a row, or to lose four in a row, win one, and then lose again.
(.5071)^5 + ((.5071)^4 * .4929 * .5071) = 0.05006091356
In order for that 5.006091356% event to matter in the first place, I must first have won the initial five in a row, so I have to multiply the probability of winning the five in a row by the probability of the subsequent events (Losing five in a row thereafter OR losing four, winning one, and then losing) occurring and then subtract that from the probability of winning five in a row in the first place. If my methodology is sound, then the result of the formula will be the probability of success given this strategy:
0.02909337405 - (0.02909337405 * 0.05006091356) = 0.02763693316
This reflects a probability of success of 2.763693316%, which is higher than the 2.63%, and moreover, if I went as far as to bet $280 when at the $720 level and then, if that failed, tried to double $440 into $880 and then tried to bet $120 followed by $240 followed by $480 and then to double the remaining $40....etc....etc....etc....the probability of success would be higher.
For example, the series where the player wins five, loses four, wins one, loses one, wins one, loses one, wins one and then wins again:
(60-120-240-480-960-920-840-680-360-720-440-880-1000 ---$120 is the last bet) adds:
(.4929 * .4929 * 4.929 * .4929 * .4929 * .5071 * .5071 * .5071 * .5071 * .4929 * .5071 * .4929 * .5071 * .4929 * .4929) = 0.00029200549 is added to the probability of winning, so:
0.02763693316 goes up to 0.02763693316 + 0.00029200549 = 0.02792893865 is the new probability of winning when you add that possible series.
If we add all other possible series' of wins, then it would probably end up close to 2.9%.
From a practical standpoint, my advice is: If you Reverse Martingale $30 into $960 by winning five PL bets in a row at Craps, the other $40 isn't really THAT important, now is it?
I love Andy! AhhhhhhhhhQuote: WizardEarlier this week there was a show on the Discovery Channel called Beating the House. Part of the show featured Andy Bloch making the claim that the best way to turn $30 into $1000 was to bet the full $30 on a single number in double-zero roulette.
He and my husband are from the same town
Do you have exactly the words he said?
I knew the dpass/odds might be the top
Bold Play on the Don't Pass was a paper from the 1980s by 3 well known math guys, including Peter Griffin
The Banker at Baccarat even with the 5% comm is at 2.81% rounded up
how about $30 Banker, after a win, to Roulette
or
craps
dinner and dancing and craps tonight!
Sally
As long as you're running simulations, do you mind determining the probability of winning with my PL Reverse Martingale never to exceed a total of $1,000 but always Reverse Martingaling if the total is under $500, and maybe the same for Don't Pass? I'm just curious, and it would take most of my life to do every possible (and, likely, practically irrelevant) series by hand.
nice try!Quote: Mission146If we add all other possible series' of wins, then it would probably end up close to 2.9%.
I show just the pass line =
0.02785283
(244/495)^5 * 0.9570755
> p <- pdoubb(960,1000,50000,244/495,1,0.000000001)
> p
[1] 0.9570755
lower than the Banker Baccarat method
but very close
Sally
Quote: mustangsallynice try!
I show just the pass line =
0.02785283
(244/495)^5 * 0.9570755
> p <- pdoubb(960,1000,50000,244/495,1,0.000000001)
> p
[1] 0.9570755
lower than the Banker Baccarat method
but very close
Sally
Thanks!
I figured there would be other methods superior to mine (and there are probably more than that), but I immediately recognized that my method is superior to Bloch's suggestion in terms of probability...00 Roulette is simply the wrong game for anything like this, regardless of the strategy.
I'm also not greedy, I'd take that $960 and run for the door...well...after checking the UX machines.
my values are calculated using 2 different methodsQuote: Mission146do you mind determining the probability of winning with my PL Reverse Martingale never to exceed a total of $1,000 but always Reverse Martingaling if the total is under $500, and maybe the same for Don't Pass? I'm just curious, and it would take most of my life to do every possible (and, likely, practically irrelevant) series by hand.
i have not completed the Wizard's pass/dpass yet
but soon will
yours is easy to do, just Bold Play
> p <- pdoubb(30,1000,50000,244/495,1,0.000000001)
> p
[1] 0.02785283
Sally
more later
Didn't you do this already with the reality TV show and the frat guys and concluded the best bet was the don't pass plus max odds?Quote: WizardEarlier this week there was a show on the Discovery Channel called Beating the House. Part of the show featured Andy Bloch making the claim that the best way to turn $30 into $1000 was to bet the full $30 on a single number in double-zero roulette.
The probability of success with that strategy is 1/38=2.63%.
An obviously superior strategy would be to bet just $27 on a single number. If you win, you'll be at $975. If you lose you'll be at $3. Either way, make the smallest bet possible that will put you at exactly $1000 on any of the available bets, or your full bankroll if you don't have enough to reach $1000 in one bet. If such optimal bet is not an integer, then round down. Keep repeating until you get to $1000 or $0. I find the probability of success is 2.81%.
However, an even better strategy of betting 1/6 of your bankroll on the pass line in craps, followed by max odds (assume 3-4-5x allowed). If this would put you over $1,000 or cause a bet that isn't evenly divisible by $1, or cause a win that isn't divisible by $1, then round the bet down. I find such a strategy has a probability of success of 2.91%.
I'm going to look at the don't pass plus laying odds next.
The question for the poll is what would be your first bet if the goal was to maximize your chance of turning $30 into $1000? Let's assume the standard casino games available in any medium-sized casino.
Quote: teddysDidn't you do this already with the reality TV show and the frat guys and concluded the best bet was the don't pass plus max odds?
As I recall, I told them to bet the pass and take the odds and grind their way up. Maybe I was wrong.
I might consider the craps table for this but you know the guy is going to try to weasel his way out of the controversy by claiming its not a one bet plan.
Bet $30 on a single number: 2.6316%
Bet $27 on a single number and grind: 2.8043%
Bet $5 on the pass line, take full odds, and grind: 2.9140%
Bet $4 on the don't pass, lay full odds, and grind: 2.9244%
Quote: WizardAs I recall, I told them to bet the pass and take the odds and grind their way up. Maybe I was wrong.
Last night at the Silverton, I lost $4,100 betting don't pass and lay odds exclusively. I didn't win a single bet the entire session.
But I sure had some "good bets."
$75 don't pass, and laying $999 on the 5 to try to win $666 was one of them.
The last time I had this bad of luck at the Silverton I bought in for $666.
I had $1 in the rail after that. So at least I wasn't broke.
In "Vegas 2047, High Limit Advantage Play Pinball" a single game and bet can take you from $30 to $1000.
Not only that, but if you have better than average skill, it can be an advantage play with positive EV.
Quote: AhighLast night at the Silverton, I lost $4,100 betting don't pass and lay odds exclusively. I didn't win a single bet the entire session.
But I sure had some "good bets."
$75 don't pass, and laying $999 on the 5 to try to win $666 was one of them.
The last time I had this bad of luck at the Silverton I bought in for $666.
I had $1 in the rail after that. So at least I wasn't broke.
In "Vegas 2047, High Limit Advantage Play Pinball" a single game and bet can take you from $30 to $1000.
Not only that, but if you have better than average skill, it can be an advantage play with positive EV.
Given the business you are in can you write that loss off on your taxes?
Professional gamer or research or something?
Quote: petroglyphGiven the business you are in can you write that loss off on your taxes?
Professional gamer or research or something?
Absolutely not. Aside from everything else, I won about that much in the previous few weeks. Losses are only good to offset wins, really when it comes to tax time. NOBODY gets a break for coming out behind gambling in the casino. You have to gamble on the stock market in order to enjoy that benefit.
I'm doing better at the tables than I am in the stock market, but even that doesn't benefit from realized losses as I trade exclusively in my Ameritrade IRA account which is all pre-tax funds.
Quote: Ahighlaying $999 on the 5 to try to win $666 ... The last time I had this bad of luck at the Silverton I bought in for $666.
Quote: odiousgambit
Trivia time! What is the sum of all the numbers on a roulette wheel?
Quote: WizardTrivia time! What is the sum of all the numbers on a roulette wheel?
Single or double zero?
where did that image come from?Quote: WizardTrivia time! What is the sum of all the numbers on a roulette wheel?
crazy code
I would do the math this way for adding up 1 to 36
37*18
works good too for 1 to 6
7*3
works good too too for 1 to 5
6*2.5
even down to 1 to 2 (add 1 to 2)
hmmm
3*1
Sally
What about the "Big Wheel" and the 45-1 slot thereon? I assume this is a horrific bet
What about a horse race betting a 33-1 shot exacta? quinella?
Quote: onenickelmiracleA couple years ago there was a news story saying the actual number of the beast was 616 due to a mistranslation somewhere. Hasn't caught on yet.
The beast can read and write but not execute. Of course you have to be talking about the octal beast for this to make sense.
Quote: Andy BlochIf you have $30 in your pocket and you want to turn it into $1000, then roulette is your only game.
Quote: Discovery Channel voice overRoulette is the best game for a quick score.
Everyone agrees that roulette the best get rich quick scheme in the casino.
Quote: WizardBet $27 on a single number and grind: 2.8043%
I improved my roulette strategy to increase the chance of turning $30 into $1,000, or turning any $x into $y. Here is my new and improved Wizard's "Quick Score" roulette strategy.
This strategy assumes that bets must be in increments of $1. In all bet calculations, round down.
Let:
b = Your bankroll
g = Your goal
1. If b>(g-b), then bet g-b on any even money bet.
2. If 3b > g, then bet (g-b)/2 on any column bet.
3. If 6b > g, then bet (g-b)/5 on any six line (six-number combination).
4. If 9b > g, then bet (g-b)/8 on any corner (four-number combination).
5. If 12b>g, then bet (g-b)/11 on any street (three-number combination).
6. If 18b>g, then bet (g-b)/17 on any split (two-number combination).
7. Otherwise, bet min(b,(g-b)/35) on any single number.
Following this strategy results in a probability of 2.8071% chance of reaching $1,000, which is 0.0028% higher than my previous strategy. In case you're wondering, the previous strategy relied on making the smallest bets possible to reach the winning goal by betting on long shots. I find it better than if you're close to the goal, maximize the probability of making it in a single bet, rather than minimizing the bet.
Quote: AxiomOfChoiceFor FPDW I get about 3.4% (from a simulation). This is particularly impressive since, sometimes you overshoot your goal.
What denomination? How much is the average final win, when there is a win?
Quote: WizardWhat denomination? How much is the average final win, when there is a win?
25c (5 coins so the top pay is $1000)
I didn't collect the stats about that but I can add some code and re-run it. I only did a million iterations (seems to be accurate within 2 significant digits)
The average bankroll when you win is 950.21 bets ( = $1187.76)
Obviously when you lose your bankroll is always 0 ($30 = 24 bets to start)
From this, we can see that you are up an average of 8.88 bets per trial. At a 0.76% edge, this implies you play an average of 1168 hands (although your median would probably be much lower)
VP Winners shows over 3% success rateQuote: AxiomOfChoice25c (5 coins so the top pay is $1000)
looks like a lot of waiting
I only went to 20k hands
2.7% 13k
2.83% 15k
3%18k
3.08% 20k
Sally
Quote: mustangsallyVP Winners shows over 3% success rate
looks like a lot of waiting
I only went to 20k hands
2.7% 13k
2.83% 15k
3%18k
3.08% 20k
Sally
I have no idea what any of those numbers mean or what VP winners is.
I had no limit on the number of hands. I just wrote a simple program that used the probability distribution from the return tables on the wizard's site, started with a 24 unit bankroll, and kept going until it hit 0 or 800 units. I did that a million times. Just two loops.
#include <cassert>
#include <iostream>
#include <map>
#include <random>
using namespace std;
typedef map<int, unsigned long long> Results;
template <class RNG>
class ResultGenerator {
public:
ResultGenerator(Results res, RNG* rng) : res_(res), rng_(rng) {
int total = 0;
for (const auto& r : res) total += r.second;
uniform_int_distribution<int> d(0, total - 1);
dist_ = d;
}
int GetResult() {
unsigned int num = dist_(*rng_);
for (const auto& r : res_) {
if (num < r.second) return r.first;
num -= r.second;
}
assert(false);
return 0;
}
private:
Results res_;
RNG* rng_;
uniform_int_distribution<int> dist_;
};
int main() {
Results res;
#if 0
// 9/6 JoB
res[799] = 2476;
res[49] = 10931;
res[24] = 236255;
res[8] = 1151221;
res[5] = 1101451;
res[3] = 1122937;
res[2] = 7444870;
res[1] = 12927890;
res[0] = 21458503;
res[-1] = 54543467;
#endif
// FPDW 100.76%
res[799] = 22;
res[199] = 204;
res[24] = 1796;
res[14] = 3202;
res[8] = 4168;
res[4] = 64938;
res[2] = 21229;
res[1] = 16784 + 56070;
res[0] = 284690;
res[-1] = 546897;
mt19937 rng(time(NULL));
ResultGenerator<mt19937> gen(res, &rng);
int wins = 0, losses = 0;
int win_amount = 0;
for (int i = 0; i < 1000000; ++i) {
int bankroll = 24;
const int goal = 800;
while (bankroll > 0 && bankroll < goal) {
int res = gen.GetResult();
bankroll += res;
}
if (bankroll >= goal) {
win_amount += bankroll;
++wins;
} else {
++losses;
}
}
cout << endl << "TOTAL:" << wins << " - " << losses << " ("
<< (double(wins*100))/(wins+losses) << "%)" << endl;
cout << "Average win when you win: " << (double)win_amount / wins << endl;
}
And the results:
$ time ../bin/sim
TOTAL:33899 - 966101 (3.3899%)
Average win when you win: 951.758
real 0m38.245s
user 0m38.232s
sys 0m0.004s
This is from a different run so the results are slightly different.
As you can see from the remnants in my code, I tried 9/6 JoB first. There is too much grinding going on here; a <100% game does not do well.
If you could find the game for pennies you would make it almost every time, although you'd probably miss your plane.
This is admittedly a silly question in a game with a player advantage; the goal becomes to bet as little as possible rather than as much as possible.
Video Poker for Winners is a software that does some calculationsQuote: AxiomOfChoiceI have no idea what any of those numbers mean or what VP winners is.
I had no limit on the number of hands. I just wrote a simple program that used the probability distribution from the return tables on the wizard's site, started with a 24 unit bankroll, and kept going until it hit 0 or 800 units. I did that a million times. Just two loops.
2.7% = probability of hitting the target at 13k hands played
it is much lower at lower hands played
added:
1.08% at 2k hands played for example
30k hands
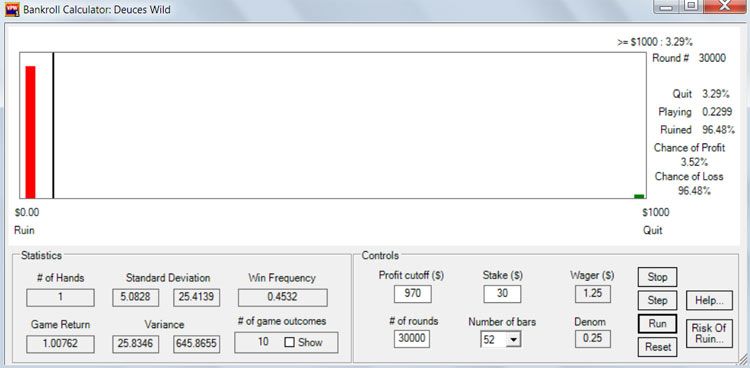
It does NOT show the average number of hands played
yours should easily show that
Sally
Quote: AxiomOfChoiceIf you can find a FPDW game for pennies, you make it to your goal about a third of the time (331 out of 1000 in my sim). Unfortunately you play an average of 781,500 hands. Somehow I doubt your $30 bankroll will get you comped for that long so I can't, in good faith, suggest this approach.
Before I knew better I played like 10 minutes of $10 craps at Caesers and asked for a $100 dinner comp. The host was not amused....
Quote: WizardQuote: odiousgambit
Trivia time! What is the sum of all the numbers on a roulette wheel?
What do you reckon, was that by design or chance? After all, no real need to have exactly 36 numbers when originally designing the game.
Did it even start out as a casino game? I havn't read up on it, but i remember someone telling me that it was originally a probability theory study by a mathematician, and he eventually went a bit crazy trying to solve it. I could be completely wrong there, this is a half remembered conversation from years ago.
I still calculate (easy in Excel or with BruceZ R code)Quote: WizardBet $27 on a single number and grind: 2.8043%
=((1/38)*0.966599621) + 0.002662643 =
2.8099476%
above is an error
corrected =((1/38)*0.966599621) + ((37/38)*0.002662643 =
0.028029406
that is $27 to 975 and even money to 1000 (1st term)
$3 left after a loss Bold it to go over 1000 (2nd term)
so it could be increased as i did not do any more to it
had a super fun weekend too!!
I now have my 1001x1001 trans matrix set up and will see
Excel can easily handle this without raising the matrix to any power
(I-S)^-1 * T
okayQuote: WizardI improved my roulette strategy
Following this strategy results in a probability of 2.8071% chance of reaching $1,000, which is 0.0028% higher than my previous strategy.
that would be easy to set up the probs in me matrix too
this weeks
Sally
Quote: mustangsallyI still calculate (easy in Excel or with BruceZ R code)
=((1/38)*0.966599621) + 0.002662643 =
2.8099476%
that is $27 to 975 and even money to 1000 (1st term)
$3 left after a loss Bold it to go over 1000 (2nd term)
so it could be increased as i did not do any more to it
had a super fun weekend too!!
I now have my 1002x1002 trans matrix set up and will see
Excel can easily handle this without raising the matrix to any power
(I-S)^-1 * T
okay
that would be easy to set up the probs in me matrix too
2.8099476% looks to be the number to beat for 00Roulette
this weeks
Sally
Hmmmm. This gigantic matrix sounds intimidating. However, I did make some improvements and got to 2.8078%. Under my strategy, if I were at $975 after winning the $27 bet, I would bet $5 on any group of six to hopefully get to $1,000.
I'm not saying my way is optimal, but it is fairly simple. I'll explain it later today.
Can I trouble you to tell me what you would with every amount from $966 to $998? Remember that bets must be in increments of $1.


