YAHTZEE strategy

Threads: 60
Posts: 5052

Joined: Feb 18, 2015

October 30th, 2020 at 3:54:48 PM permalink

Quote: DRich
Do you have or have you read Olaf's Yahtzee book? He used to be a slot machine designer and BJ strategy guy.

No, I have never heard of it until this moment. I imagine that he has probably worked out all the expectations for most of the situational decisions that I am proposing.

I enjoy working on the mathematics of game strategies. Many of us have worked out the probabilities of many blackjack decisions even though books and the WOO site are available. The same is true for many casino games -many of us do the math ourselves. I was proposing that we do that for Yahtzee; if no one else is interested I'll just go ahead an do it myself unless I lose interest.

Last edited by: gordonm888 on Oct 30, 2020

So many better men, a few of them friends, are dead. And a thousand thousand slimy things live on, and so do I.

FinsRule

FinsRule

Threads: 128
Posts: 3914

Joined: Dec 23, 2009

Thanked by

October 30th, 2020 at 3:56:59 PM permalink

Yahtzee is going to be hard. There�s so many scenarios when you figure in the top half bonus.

charliepatrick

Threads: 39
Posts: 2946

Joined: Jun 17, 2011

Thanked by

October 30th, 2020 at 5:14:40 PM permalink

Quote: gordonm888
...Any general comments on the Yahtzee Strategy problem are welcome as well!

There's an interesting read at https://en.wikipedia.org/wiki/Yahtzee which describes some of the decisions. It looks a tough game to analyse.

gordonm888
Administrator

Threads: 60
Posts: 5052

Joined: Feb 18, 2015

October 30th, 2020 at 5:54:35 PM permalink

Quote: charliepatrick
There's an interesting read at https://en.wikipedia.org/wiki/Yahtzee which describes some of the decisions. It looks a tough game to analyse.

Thanks Charlie. I also found this viewchart presentation from the Netherlands Optimal YAHTZEE strategy . Its slow to get going, but the second half of it has some interesting analysis.

So many better men, a few of them friends, are dead. And a thousand thousand slimy things live on, and so do I.

gordonm888
Administrator

Threads: 60
Posts: 5052

Joined: Feb 18, 2015

Thanked by

October 30th, 2020 at 6:17:45 PM permalink

Here is some statistical information I found for the outcomes (without the Extra Yahtzee Bonus) when its your last turn and these are the single remaining Yahtzee hand category you are targeting.

LAST TURN Category	Expected Value	Prob. of Zero Pts, %
Aces	2.11	6.49
Twos	4.21	6.49
Threes	6.32	6.49
Fours	8.43	6.49
Fives	10.53	6.49
Sixes	12.64	6.49

3 of a kind	15.19	28.76
4 of a kind	5.61	72.26
Full House	9.15	63.39
Short Straight	18.48	38.40
Long Straight	10.61	73.47
Yahtzee	2.3	95.40
Chance	23.33	0.00

This is from the link I referenced in my previous post.

So many better men, a few of them friends, are dead. And a thousand thousand slimy things live on, and so do I.

unJon

unJon

Threads: 14
Posts: 4599

Joined: Jul 1, 2018

October 30th, 2020 at 6:40:16 PM permalink

Amazing thread. Thanks for starting it.

The race is not always to the swift, nor the battle to the strong; but that is the way to bet.

charliepatrick

Threads: 39
Posts: 2946

Joined: Jun 17, 2011

Thanked by

October 31st, 2020 at 2:45:52 AM permalink

Quote: gordonm888
Here is some statistical information...when its your last turn...

I can see the recursive approach, similar to how to do BJ. Also I noticed that One thru Sixes are always going to be X thru 6X, since it's just a matter of how many of "what you want" you get multiplied by the value.

So I guess at N options to go you look at the {throw,# rolls left} and which dice to keep. Then like BJ look at where you're at and where you might land up and work out the EVs (or expected score). I suspect once you get going (programming wise) it's a matter of cranking a very big handle.

I feel a challenge looming!

gordonm888
Administrator

Threads: 60
Posts: 5052

Joined: Feb 18, 2015

October 31st, 2020 at 11:00:14 AM permalink

Quote: charliepatrick
I can see the recursive approach, similar to how to do BJ. Also I noticed that One thru Sixes are always going to be X thru 6X, since it's just a matter of how many of "what you want" you get multiplied by the value.

So I guess at N options to go you look at the {throw,# rolls left} and which dice to keep. Then like BJ look at where you're at and where you might land up and work out the EVs (or expected score). I suspect once you get going (programming wise) it's a matter of cranking a very big handle.

I feel a challenge looming!

Parts of the problem involving the three rolls in a given round can be addressed by Markhov chains e.g., pursuing 6's, i.e. whenever you have one 6 you will roll four dice and the outcome probabilities for one, two, three, four, five 6's are always the same; when you start a roll with 2 sixes you will roll 4 dice and there will be another set of transiotion probabilities for two, three, four and five dice, etc.

The problem comes when you are rolling for Yahtzee or 4oak and you get say, two 6s on the first roll, but the second roll is three 4's, then you switch to fours. The rolls then switch to looking for 4s.

So many better men, a few of them friends, are dead. And a thousand thousand slimy things live on, and so do I.

charliepatrick

Threads: 39
Posts: 2946

Joined: Jun 17, 2011

October 31st, 2020 at 7:21:22 PM permalink

Quote: gordonm888
Here is some statistical information...

I agree with the lower numbers on the assumption that on the last round (of three rolls) a yahtzee can provide a winner in any of the sections (except "chance"). I don't quite get the top numbers (currently getting near 2.08 not 2.106481), assuming an incorrect yahtzee is 0. I'll have another look at my code tomorrow as I possibly have an error when the player should re-roll everything which can't happen in the bottom half.

Aces	2.079 564
Twos	4.159 128
Threes	6.238 692
Fours	8.318 256
Fives	10.397 819
Sixes	12.477 383
3 of a kind	15.194 661
4 of a kind	5.611 263
Full House	9.153 620
Short Straight	18.477 282
Long Straight	10.612 741
Yahtzee	2.301 432
Chance	23.330 717

Last edited by: charliepatrick on Oct 31, 2020

charliepatrick

Threads: 39
Posts: 2946

Joined: Jun 17, 2011

November 1st, 2020 at 5:17:02 AM permalink

Now I agree - I guess there are situations where you do re-roll everything in the chance saloon, I'm guessing when you've seen all ten dice (1st round and 2nd round) rolled less than 4! Also a warm feeling that chance is a fraction.

Aces	2.106 481
Twos	4.212 963
Threes	6.319 444
Fours	8.425 926
Fives	10.532 407
Sixes	12.638 889
3 of a kind	15.194 661
4 of a kind	5.611 263
Full House	9.153 620
Short Straight	18.480 750
Long Straight	10.612 742
Yahtzee	2.301 432
Chance	23.333 333

Wizard
Administrator

Threads: 1493
Posts: 26500

Joined: Oct 14, 2009

November 1st, 2020 at 9:28:32 PM permalink

Let's say it's your first turn and after the third roll you have #$%*, like 1-2-2-4-6. Which field should you fill in?

I'd probably fill in 4 for twos.

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

rsactuary

Threads: 29
Posts: 2315

Joined: Sep 6, 2014

November 1st, 2020 at 9:55:40 PM permalink

Quote: Wizard
Let's say it's your first turn and after the third roll you have #$%*, like 1-2-2-4-6. Which field should you fill in?

I'd probably fill in 4 for twos.

Personally, I'd fill in the 1. If you fill in the two 2s, you have to get a fourth 3, 4, 5 or 6 to get the upper bonus. If you fill in the 1, you have the additional benefit of being able to get four 2s to get the bonus.

Wizard
Administrator

Threads: 1493
Posts: 26500

Joined: Oct 14, 2009

November 2nd, 2020 at 5:25:50 AM permalink

Quote: rsactuary
Personally, I'd fill in the 1. If you fill in the two 2s, you have to get a fourth 3, 4, 5 or 6 to get the upper bonus. If you fill in the 1, you have the additional benefit of being able to get four 2s to get the bonus.

Good point. It just feels so feeble but write in a "1," but I suspect you're right.

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

rsactuary

Threads: 29
Posts: 2315

Joined: Sep 6, 2014

Thanked by

November 2nd, 2020 at 6:35:57 AM permalink

Of course, papers have been written...

http://gunpowder.cs.loyola.edu/~jglenn/research/optimal_yahtzee.pdf

and...

http://www-set.win.tue.nl/~wstomv/misc/yahtzee/slides-2up.pdf

Here is an optimal strategy analyzer which suggests playing the two 2s instead of the one 1. Seems counter-intuitive to me. I guess the advantage of having the ability to get four 2s on a future roll is more than offset by the probability of not getting at least two 2s again?

http://www-set.win.tue.nl/~wstomv/misc/yahtzee/osyp.php

gordonm888
Administrator

Threads: 60
Posts: 5052

Joined: Feb 18, 2015

November 2nd, 2020 at 10:46:55 AM permalink

These results are from the Verhoeff paper on Optimal Yahtzee Strategies.

1. First turn, first roll: 1 1 6 6 6
a. Keep: 6 6 6 _____265.12 +/- 61
b. Keep all and score 25 in Full House: 253.91 +/- 57
I suspect the ranking of these options would be flipped if this roll occurred late in the game, because Full House is so hard to get points for when you target it, rather than get it accidently. Although it probably depends upon what is needed on top to get a total of 63 or higher.

2. First turn, second roll: 1 1 3 4 6
a. Keep 3 4: 245.17 +/- 57
b. Keep 1 1: 245.14 +/- 57
c. Keep 4: 244.96
d. Keep 3: 244.74
e. Keep none: 244.55
f. Keep 6: 244.52
The fact that �f: Keep 6� scores the lowest seems to show the importance of targeting the SIXES when your first roll has at least two 6s. Scoring at least 18 with a shot at scoring 24 in SIXES is one of the keys to getting a high score.

3. First turn, third roll: 6 6 6 6 1
a. Score 24 in Sixes: 268.23 +/- 53
b. Score 25 in Four of a Kind: 260.54 +/- 54

I suspect the difference between these two options would be smaller (by 4) if it were 6 6 6 6 5.

Last edited by: gordonm888 on Nov 2, 2020

So many better men, a few of them friends, are dead. And a thousand thousand slimy things live on, and so do I.

terapined

terapined

Threads: 89
Posts: 6193

Joined: Dec 1, 2012

November 2nd, 2020 at 11:22:46 AM permalink

Ive been playing lately
cool game
Have it on my switch, part of a 50 game package of games
My strategy is to try to hit the straight and take ones or 2's or 3's when I dont because those dont score much anyway
Overall, seems whoever can hit a straight 1st will win.
You hit it early, you will score high
You hit it late, you will score low

Its just a forum. Nothing here to get obsessed about.

Wizard
Administrator

Threads: 1493
Posts: 26500

Joined: Oct 14, 2009

November 17th, 2020 at 7:23:27 AM permalink

At the end of your first turn you have 6-6-6-6-5. Do you fill in 24 for sixes or 29 for a four of a kind?

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

rsactuary

Threads: 29
Posts: 2315

Joined: Sep 6, 2014

November 17th, 2020 at 7:45:43 AM permalink

Quote: Wizard
At the end of your first turn you have 6-6-6-6-5. Do you fill in 24 for sixes or 29 for a four of a kind?

I'm going for 24 for sixes in a heartbeat as it practically ensures you're going to get the 35 point bonus.

Wizard
Administrator

Threads: 1493
Posts: 26500

Joined: Oct 14, 2009

November 17th, 2020 at 9:23:52 AM permalink

Quote: rsactuary
I'm going for 24 for sixes in a heartbeat as it practically ensures you're going to get the 35 point bonus.

I'm not saying you're wrong, but often I have to put in a zero for a four of a kind. If you play the 4K, that's 29 points and you still have a lot of hope at the 35 bonus points. I think I achieve the bonus about 2/3 of the time.

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

rsactuary

Threads: 29
Posts: 2315

Joined: Sep 6, 2014

November 17th, 2020 at 9:56:36 AM permalink

duplicate

Last edited by: rsactuary on Nov 17, 2020

rsactuary

Threads: 29
Posts: 2315

Joined: Sep 6, 2014

November 17th, 2020 at 9:56:36 AM permalink

Quote: Wizard
I'm not saying you're wrong, but often I have to put in a zero for a four of a kind. If you play the 4K, that's 29 points and you still have a lot of hope at the 35 bonus points. I think I achieve the bonus about 2/3 of the time.

I ran this through the optimal strategy link above and the top three results were as follows (assuming the first roll of a game):

Score 24 in Sixes 268.23±53
Score 29 in Four of a Kind 264.54±54
Score 29 in Three of a Kind 254.96±56 -- obviously no one is going to do this.

Wizard
Administrator

Threads: 1493
Posts: 26500

Joined: Oct 14, 2009

November 17th, 2020 at 10:07:07 AM permalink

Quote: rsactuary
I ran this through the optimal strategy link above and the top three results were as follows (assuming the first roll of a game):

Score 24 in Sixes 268.23±53
Score 29 in Four of a Kind 264.54±54
Score 29 in Three of a Kind 254.96±56 -- obviously no one is going to do this.

Thanks. Good to know.

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

gordonm888
Administrator

Threads: 60
Posts: 5052

Joined: Feb 18, 2015

November 17th, 2020 at 2:30:23 PM permalink

Quote: rsactuary
I ran this through the optimal strategy link above and the top three results were as follows (assuming the first roll of a game):

Score 24 in Sixes 268.23±53
Score 29 in Four of a Kind 264.54±54
Score 29 in Three of a Kind 254.96±56 -- obviously no one is going to do this.

But I do think that the answer is different if it is late in the game and you roll 66665 and you still have SIXES and FOUR OF A KIND open and four or five rounds to go - especially if you only need 18 points in SIXES to get the 35 point bonus.

So many better men, a few of them friends, are dead. And a thousand thousand slimy things live on, and so do I.

Gialmere

Gialmere

Threads: 44
Posts: 2939

Joined: Nov 26, 2018

November 17th, 2020 at 5:32:50 PM permalink

Quote: terapined
Ive been playing lately
cool game
Have it on my switch, part of a 50 game package of games
My strategy is to try to hit the straight and take ones or 2's or 3's when I dont because those dont score much anyway
Overall, seems whoever can hit a straight 1st will win.
You hit it early, you will score high
You hit it late, you will score low

Concerning straights, a few scenarios...

What would you do if...

1) It's your first turn and you roll a 2-2-4-5-6?

2) It's your first turn and you roll a 2-3-4-6-6?

3) You scored a full house on your first turn and the first roll of your second turn is 2-2-3-4-4?

Have you tried 22 tonight? I said 22.

Wizard
Administrator

Threads: 1493
Posts: 26500

Joined: Oct 14, 2009

November 17th, 2020 at 6:15:19 PM permalink

Quote: Gialmere
Concerning straights, a few scenarios...

What would you do if...

1) It's your first turn and you roll a 2-2-4-5-6?

2) It's your first turn and you roll a 2-3-4-6-6?

3) You scored a full house on your first turn and the first roll of your second turn is 2-2-3-4-4?

I have no idea if this is right, but my hunch would be to...

1. Keep the 2-2. Second choice would be to keep the 2-4-5 and go for either straight.
2. Keep the 6-6 for sure.
3. Keep the 4-4

Anyone know where we can play Yahtzee against each other? There is a Facebook game that plays it, but it doesn't follow the proper rule on more than one Yahtzee.

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

rsactuary

Threads: 29
Posts: 2315

Joined: Sep 6, 2014

November 17th, 2020 at 7:10:03 PM permalink

Quote: Gialmere
Concerning straights, a few scenarios...

What would you do if...

1) It's your first turn and you roll a 2-2-4-5-6?

2) It's your first turn and you roll a 2-3-4-6-6?

3) You scored a full house on your first turn and the first roll of your second turn is 2-2-3-4-4?

According to the optimizer:

1) Keep 2 2 _ _ _ 250.56±59

Keep _ _ _ 5 _ 249.94±58

Keep _ _ 4 5 _ 249.89±58

Keep _ _ 4 _ _ 249.88±58

Keep 2 _ 4 5 _ 249.87±57

2) Keep _ _ _ 6 6 253.94±59

Keep _ _ 4 6 6 251.74±58 <--- interesting...

Keep _ 3 _ 6 6 251.71±58

Keep 2 _ _ 6 6 251.64±58

Keep 2 3 4 _ _ 250.42±58

3) Keep _ _ _ 4 4 251.54±56 (assumes full house is not available)

Keep 2 _ 3 4 _ 249.99±55

Keep _ _ 3 4 4 249.86±55

Keep 2 2 _ _ _ 249.67±56

DogHand

DogHand

Threads: 2
Posts: 1525

Joined: Sep 24, 2011

November 17th, 2020 at 7:30:17 PM permalink

Quote: Wizard
I have no idea if this is right, but my hunch would be to...

1. Keep the 2-2. Second choice would be to keep the 2-4-5 and go for either straight.
2. Keep the 6-6 for sure.
3. Keep the 4-4

Anyone know where we can play Yahtzee against each other? There is a Facebook game that plays it, but it doesn't follow the proper rule on more than one Yahtzee.

Wizard,

Use the multiplayer option here:

https://cardgames.io/yahtzee/

Dog Hand

Gialmere

Gialmere

Threads: 44
Posts: 2939

Joined: Nov 26, 2018

November 18th, 2020 at 7:37:41 PM permalink

What if, instead of a 2-3-4-6-6, you roll a 1-1-3-4-5 to begin your first turn.

I'm just wondering if there is any first turn, first roll scenario where going for the (non pat) straight becomes optimal.

Have you tried 22 tonight? I said 22.

rsactuary

Threads: 29
Posts: 2315

Joined: Sep 6, 2014

November 18th, 2020 at 7:43:41 PM permalink

Quote: Gialmere
What if, instead of a 2-3-4-6-6, you roll a 1-1-3-4-5 to begin your first turn.

I'm just wondering if there is any first turn, first roll scenario where going for the (non pat) straight becomes optimal.

I'm going for the 3-4-5 every time, in this situation.

Wizard
Administrator

Threads: 1493
Posts: 26500

Joined: Oct 14, 2009

November 19th, 2020 at 5:29:31 AM permalink

Quote: DogHand
Wizard,

Use the multiplayer option here:

https://cardgames.io/yahtzee/

Dog Hand

Thanks! Who is up for a game? I'll keep an eye on this thread for a spontaneous challenge.

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

Gialmere

Gialmere

Threads: 44
Posts: 2939

Joined: Nov 26, 2018

November 19th, 2020 at 8:27:02 AM permalink

Quote: rsactuary
I'm going for the 3-4-5 every time, in this situation.

How about a 1-1-4-5-6?

Have you tried 22 tonight? I said 22.

terapined

terapined

Threads: 89
Posts: 6193

Joined: Dec 1, 2012

November 19th, 2020 at 8:34:43 AM permalink

Quote: Gialmere
Concerning straights, a few scenarios...

What would you do if...

1) It's your first turn and you roll a 2-2-4-5-6?

2) It's your first turn and you roll a 2-3-4-6-6?

3) You scored a full house on your first turn and the first roll of your second turn is 2-2-3-4-4?

Chuckle
I was playing quite a bit on my switch due to this thread
But
I just finished the Queens Gambit, great netflix series.
I've been playing a lot of chess on my switch now
I'm a pawn to King 4 opening person my whole life
Been playing a lot on my switch using Queens gambit opening and really loving my position.
The series is fascinating as it uses real historical games picked by Gary Kasporov. I've watched analysis of those games on youtube.

Its just a forum. Nothing here to get obsessed about.

Wizard
Administrator

Threads: 1493
Posts: 26500

Joined: Oct 14, 2009

November 19th, 2020 at 9:26:42 AM permalink

Quote: terapined
I just finished the Queens Gambit,...

I think I'll split off your Queen's Gambit post to it's own thread, as I thought the show was outstanding too. However, feel free to make your own original post, if you wish.

Back to Yahtzee, what would be the optimal strategy and mean score if the only thing left on the card was Chance?

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

Wizard
Administrator

Threads: 1493
Posts: 26500

Joined: Oct 14, 2009

November 19th, 2020 at 6:38:31 PM permalink

I'm in a mood for Yahtzee!

Who wants to play right now?

I'm Wiz.

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

gordonm888
Administrator

Threads: 60
Posts: 5052

Joined: Feb 18, 2015

November 19th, 2020 at 8:18:25 PM permalink

Quote: rsactuary
According to the optimizer:

1) Keep 2 2 _ _ _ 250.56±59

Keep _ _ _ 5 _ 249.94±58

Keep _ _ 4 5 _ 249.89±58

Keep _ _ 4 _ _ 249.88±58

Keep 2 _ 4 5 _ 249.87±57

2) Keep _ _ _ 6 6 253.94±59

Keep _ _ 4 6 6 251.74±58 <--- interesting...

Keep _ 3 _ 6 6 251.71±58

Keep 2 _ _ 6 6 251.64±58

Keep 2 3 4 _ _ 250.42±58

3) Keep _ _ _ 4 4 251.54±56 (assumes full house is not available)

Keep 2 _ 3 4 _ 249.99±55

Keep _ _ 3 4 4 249.86±55

Keep 2 2 _ _ _ 249.67±56

When the margins are 1 to 2 tenths of a point and the standard deviations change from ±55 to ±59, it s a bit hard to feel conviction about the results. Maybe the results are just not being presented in a very good way.

So many better men, a few of them friends, are dead. And a thousand thousand slimy things live on, and so do I.

rsactuary

Threads: 29
Posts: 2315

Joined: Sep 6, 2014

November 19th, 2020 at 8:45:14 PM permalink

Quote: gordonm888
When the margins are 1 to 2 tenths of a point and the standard deviations change from ±55 to ±59, it s a bit hard to feel conviction about the results. Maybe the results are just not being presented in a very good way.

I think what it really means is that in the first few rolls, the order you do things doesn't really matter. But.... if you're the type to pay attention to micro VP edges.....

Mosca

Mosca

Threads: 191
Posts: 4140

Joined: Dec 14, 2009

November 21st, 2020 at 8:06:41 AM permalink

I play a lot of yahtzee! Haven't visited in a while.

There are a few different strategies, depending on what you want to accomplish. You can play to get the highest score, you can play to optimize the highest score for the game that you're playing, you can play to beat the other player, or you can play to avoid losing.

Playing for the highest score? Every roll try to get a yahtzee. You'll wind up with a lot of games in the 100s, and every now and then you'll hit five hundred or more.

Play to optimize your score? That's the strategy most mentioned in this topic.

Play to beat the other player? If it's the last few rolls and you need two Yotz, you gotta do what you gotta do.

Play to avoid losing? This is a variation of the optimum strategy, I can best describe it as thinking "Where am I going to put this roll if I miss it?" In this strategy, 3oak, ss, 1s and 2s, and Chance are all safety spots, places to put rolls that missed. If you roll 3 1s, and already have them filled, you can shoot for Yotz, knowing it might only be 10 in the 3oak. But it's not 0 in the Yotz. If you missed your 4s, you can zero your 1s. You still need four 4s, but that's down the road.

I play at Board Game Arena, https://en.boardgamearena.com/gamepanel?game=yatzy

It is free. You can play with specific opponents, or random, anywhere from 2 to 5 players. There are players from all over the world. There is a nice chat feature for use during the games. It helps to learn how to say "Good Luck!" and "Good Game!" in French, Spanish, German, and Italian. Also chess, checkers, backgammon, hearts, spades, etc.

Wiz, I'll play you, but I can't right now I'm at work.

A falling knife has no handle.

Wizard
Administrator

Threads: 1493
Posts: 26500

Joined: Oct 14, 2009

December 15th, 2020 at 5:11:32 PM permalink

I've been playing quite a bit of Yahtzee online. I still haven't seen any WoV members in the player pool.

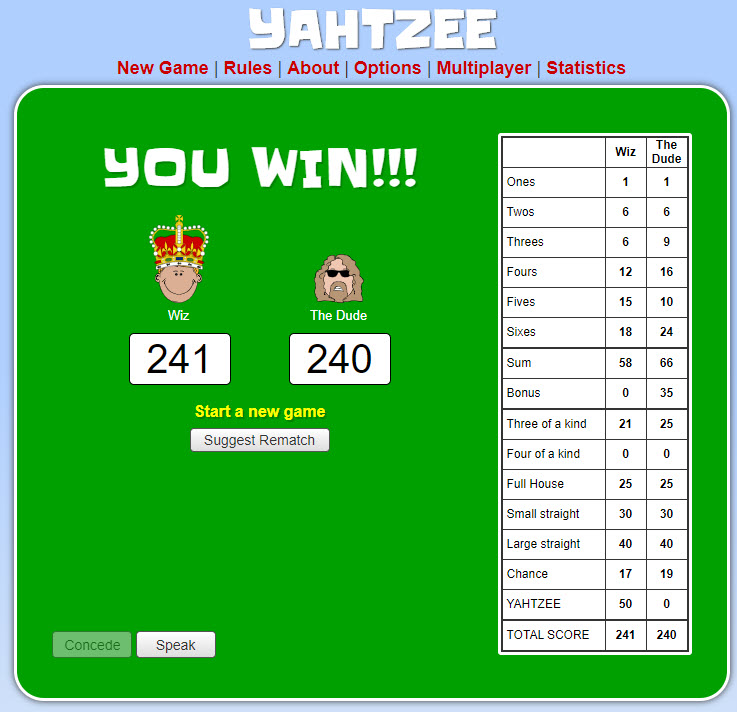
New high score today!

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

DRich

DRich

Threads: 86
Posts: 11721

Joined: Jul 6, 2012

December 15th, 2020 at 5:25:10 PM permalink

Wizard, have you read Olaf Vancura's book on Yahtzee?

At my age, a "Life In Prison" sentence is not much of a deterrent.

Wizard
Administrator

Threads: 1493
Posts: 26500

Joined: Oct 14, 2009

December 15th, 2020 at 8:26:11 PM permalink

Quote: DRich
Wizard, have you read Olaf Vancura's book on Yahtzee?

I have it, but only skimmed it. As I recall, it seemed more academic than strategic.

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

Mosca

Mosca

Threads: 191
Posts: 4140

Joined: Dec 14, 2009

December 18th, 2020 at 3:50:39 PM permalink

Quote: Wizard
I've been playing quite a bit of Yahtzee online. I still haven't seen any WoV members in the player pool.

New high score today!

My daughter laid a 502 on me today. What stunk was I had a 313.

A falling knife has no handle.

Wizard
Administrator

Threads: 1493
Posts: 26500

Joined: Oct 14, 2009

Thanked by

December 23rd, 2020 at 10:17:11 PM permalink

Don't you hate it when people quit on you?!! In my first six turns I had two Yahtzees and a large straight. Then my opponent quit. No closure to the game. No opportunity to beat my high score of 498. I think whoever runs this game should give you the opportunity to finish it out alone.

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

SOOPOO

SOOPOO

Threads: 122
Posts: 11009

Joined: Aug 8, 2010

December 24th, 2020 at 7:41:06 AM permalink

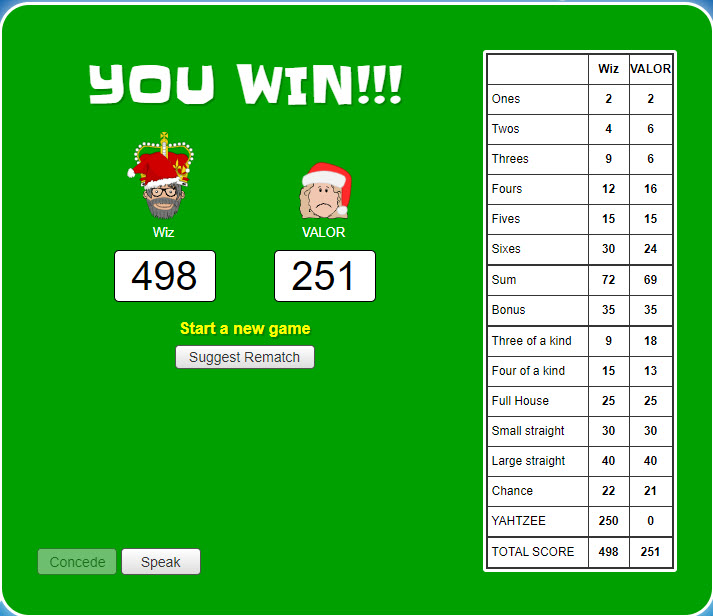
Quote: Wizard
Don't you hate it when people quit on you?!! In my first six turns I had two Yahtzees and a large straight. Then my opponent quit. No closure to the game. No opportunity to beat my high score of 498. I think whoever runs this game should give you the opportunity to finish it out alone.

I used to play bridge online on POGO.com. Everyone had a rating, and your rating would go up or down depending on whether you won or lost, and it took into account the rating of your partner and opponents. After a while my rating reached near the top. But then you would play the occasional opponent who would not quit or resign or finish, but would stall. So I would be stuck mid game unless I wanted to resign. You would make note of the scoundrel and never play with him/her again, but I eventually got frustrated enough that I don�t play there anymore.

Joeman

Joeman

Threads: 36
Posts: 2414

Joined: Feb 21, 2014

December 24th, 2020 at 9:00:40 AM permalink

I sometimes play over at Board Game Arena. Each player there has a Reputation stat attached to their account. Things like stalling, quitting, abusive language, etc. may/will cause your Reputation to be lowered. In addition, you can filter available opponents based on their Reputation score so that you won't have to play someone with a Reputation below a certain threshold.

However, there are very few of the classic games there. They are more focused on newer games.

"Dealer has 'rock'... Pay 'paper!'"

Wizard
Administrator

Threads: 1493
Posts: 26500

Joined: Oct 14, 2009

December 24th, 2020 at 11:56:18 AM permalink

I should join one of these board game membership sites where members are held accountable for bad etiquette. Can anyone recommend one that emphasizes the classic games?

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

terapined

terapined

Threads: 89
Posts: 6193

Joined: Dec 1, 2012

December 24th, 2020 at 1:53:05 PM permalink

We should arrange a time ahead of time to all get on at once and play each other

Its just a forum. Nothing here to get obsessed about.

Wizard
Administrator

Threads: 1493
Posts: 26500

Joined: Oct 14, 2009

December 24th, 2020 at 7:08:33 PM permalink

Quote: terapined
We should arrange a time ahead of time to all get on at once and play each other

I agree. How about we try 7:00 PM PST and whoever shows up shows up shows up?

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

Wizard
Administrator