Some stats for the Make EM All bonus bet

I get some interesting stats for you guys for the bonus bet.

I practiced and rolled 316 times to make the bonus

I failed to make the bonus within 271 rolls of dice

@ the 44th trial (316 rolls of dice)
I made the bonus @practice
The bonus would be $875 ($175 x$5)

@casino
I would pay $215 to shoot 43 times (in casino linko: reset and reload 43 times @$5 each time)

I would get paid $875 ($175 x$5) and make $660 profit ($875-215)

See the details in the link for my excel spreadsheet
Click here to see my Excel spreadsheet

When simulating this kind of a bet, a hand should end when a 7 is rolled or the goal is achieved, not both.

In trial #44 it appears you hit all numbers including the 7. That doesn't show me that you won the bet.

Quote: AutomaticMonkey

When simulating this kind of a bet, a hand should end when a 7 is rolled or the goal is achieved, not both.

In trial #44 it appears you hit all numbers including the 7. That doesn't show me that you won the bet.
link to original post

You're right.
Thanks for pointing that out.
Now I've made a footnote on the Excel: " Note: *7 popped up after I made the bonus"

Click here to see my Excel spreadsheet

Quote: AutomaticMonkey

When simulating this kind of a bet, a hand should end when a 7 is rolled or the goal is achieved, not both.

In trial #44 it appears you hit all numbers including the 7. That doesn't show me that you won the bet.
link to original post

I for one am assuming that, in this instance, every trial continues until a 7 is rolled, and then the numbers are checked to see if every one of the 11 results came up at least once. The only "problem" would be, the total number of rolls would be higher than what would actually happen.

Quote: ThatDonGuy

Quote: AutomaticMonkey

When simulating this kind of a bet, a hand should end when a 7 is rolled or the goal is achieved, not both.

In trial #44 it appears you hit all numbers including the 7. That doesn't show me that you won the bet.
link to original post

I for one am assuming that, in this instance, every trial continues until a 7 is rolled, and then the numbers are checked to see if every one of the 11 results came up at least once. The only "problem" would be, the total number of rolls would be higher than what would actually happen.
link to original post

You are correct.

I've overstated the rolls by 1

@roll#316
The 7 popped up.

I've programed to end the recording @ that trial#44th
whenever the 7 pops up.

The new trial#45th began after that ending.

See the revised info below

Quote: Armagedden

Quote: ThatDonGuy

Quote: AutomaticMonkey

When simulating this kind of a bet, a hand should end when a 7 is rolled or the goal is achieved, not both.

In trial #44 it appears you hit all numbers including the 7. That doesn't show me that you won the bet.
link to original post

I for one am assuming that, in this instance, every trial continues until a 7 is rolled, and then the numbers are checked to see if every one of the 11 results came up at least once. The only "problem" would be, the total number of rolls would be higher than what would actually happen.
link to original post

You are correct.

I've overstated the rolls by 1

@roll#316
The 7 popped up.
link to original post

Was the 315th roll a 2? If not, then you already had all 10 of the non-7 numbers after 314 rolls, so the length of that trial is less than 315.

Also remember that you have to report an additional trial, that started with the roll after the last roll of the winning one, and ended with the 7 that you reported as roll #316 of the winning trial.

Not that it really matters, but some casinos let you remake the bet after the bet is won, so it wouldn’t stop only when a 7 is hit.

Also most casinos only pay 150:1 these days.

@ThatDonGuy,

Roll#307 was a 12 which made the bonus.
Roll#316 was a 7 which ended the trial#44.

My program automatically resets and restarts @trial#45 in the next column.

See the spreadsheet for details
Click here to see my Excel spreadsheet

So I rolled 307 times exactly to make the bonus, not 315 nor 316 as prevously stated.

Thanks for encouraging me to look back @ the details to get the correct info

From Reddit:
Numbers From Wizard of Odds

Small/Tall if pays 34 to 1 has 7.76% house edge, if it pays 30 to 1 has an 18.30% house edge

Make em All if it pays 175 to 1 has 7.47% house edge, and 150 to 1 has 20.61% house edge
****************************
I'm trying to figure out if the ATS bets lose on come-out 7's. I think they do. So that messes up shooters who use every come-out opportunity to roll 7-11's and then don't because they don't want to lose their Come bets or the ATS bets.
*****************************
From Reddit:
If you bet the same on the pass line as you do on ATS, the come-out 7 doesn't hurt. You just use the winnings from the pass line to repay the ATS. Sure you are technically down, as those would be in your pile otherwise, but I view it as a neutral roll. It's basically as if the roll never happened.

Point seven, though, hurts.

@ChampChange

Here are more interesting stats

I had rolled 579 more times in between 2 bonuses

Look at roll#10 thru roll#33 for the bonus-numbers in red.

then look at roll#612 thru roll#648 for the other bonus-numbers in red


Click here to see the details in Excel

@ChampChange

Here are more interesting stats

I had rolled 579 more times in between 2 bonuses

Look at roll#10 thru roll#33 for the bonus-numbers in red.

then look at roll#612 thru roll#648 for the other bonus-numbers in red


Click here to see the details in Excel

@now I get some really lucky rolls @ practice

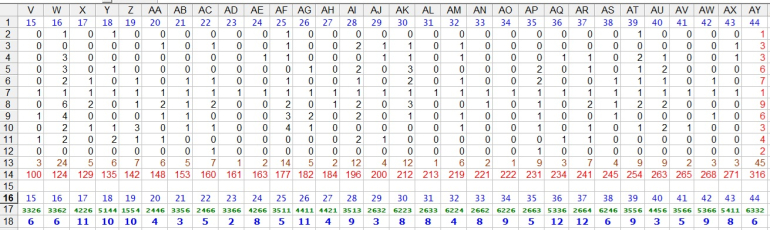
I've rolled 28 times before 7outs


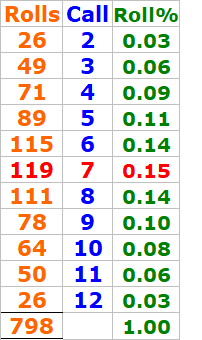
Here is a recap for rolls in percentages:





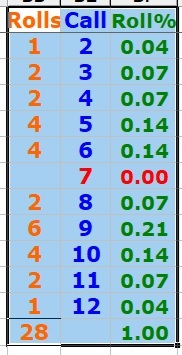
Here are details for each of 28 rolls:






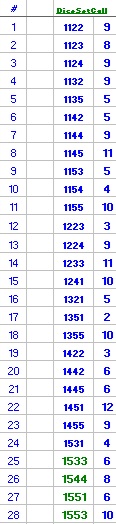
I got a 7out @roll#29

This was the quickest luckiest way to make the "make'EM all bonus"

An interesting strategy around people that are obsessed with the ATS bet, is simply making a corresponding X+Y come/PL bet, where X is how much you spent on the ATS and Y was... some other number I'm forgetting at the moment. John from ProCraps posted the strategy about a year or more ago on his youtube channel and he had a spreadsheet for what to bet at what level of ATS betting you wanted to do.

In theory, you use the Come/PL wins to fuel the ATS bet. Assuming a normal distribution of Come/PL wins during your session, it would "guarantee" you a lot of paid-for stabs at the ATS, which is your primary goal for that session.

Flipside, I've bet the ATS a few times when i wanted to bet extra heavy on the DC/PL side, as a weird hedge in case a shooter got hot during the roll. For my bet level, I do a 10/5/10 or 22/6/22 spread, since making tall or all is much more frequent during any particular session when someone is at the tables.

Yesterday I rolled 183 times @practice and failed to make'EM-ALL

@now I get some good rolls @ practice

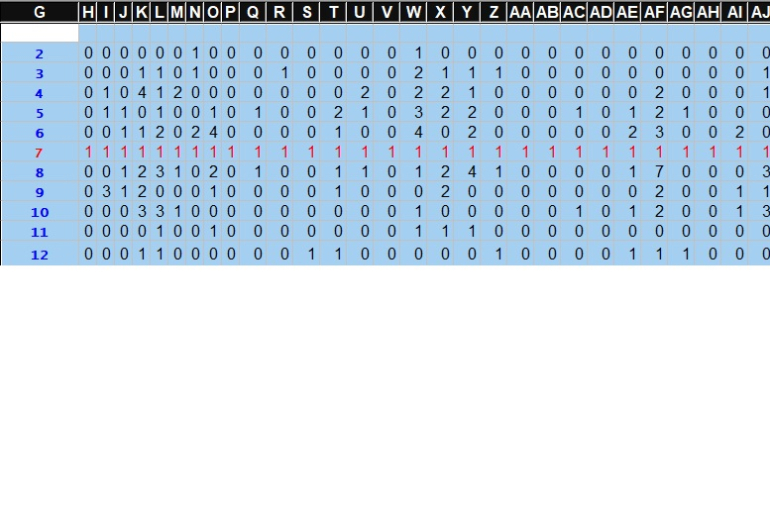
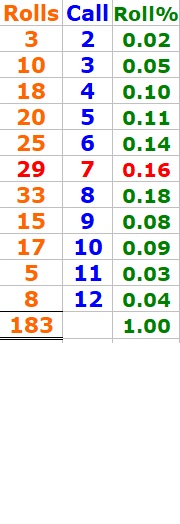
I've rolled 106 times


Here is a recap for rolls in percentages:




Within 106 rolls
I've made the "make'EM all bonus", see column#16

Here are the roll-details of the "make'EM all bonus"

@now I've just finished my practice

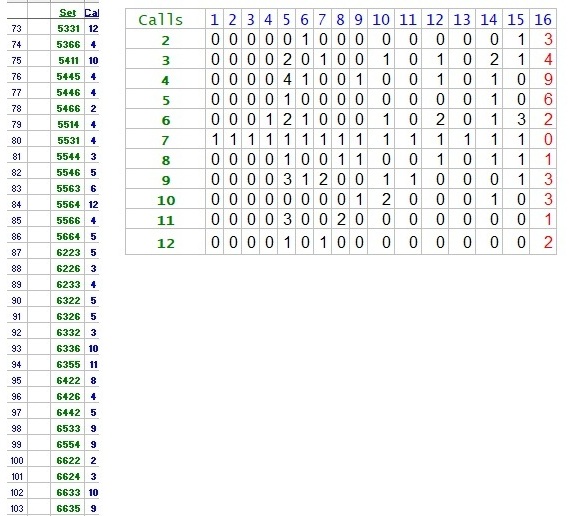
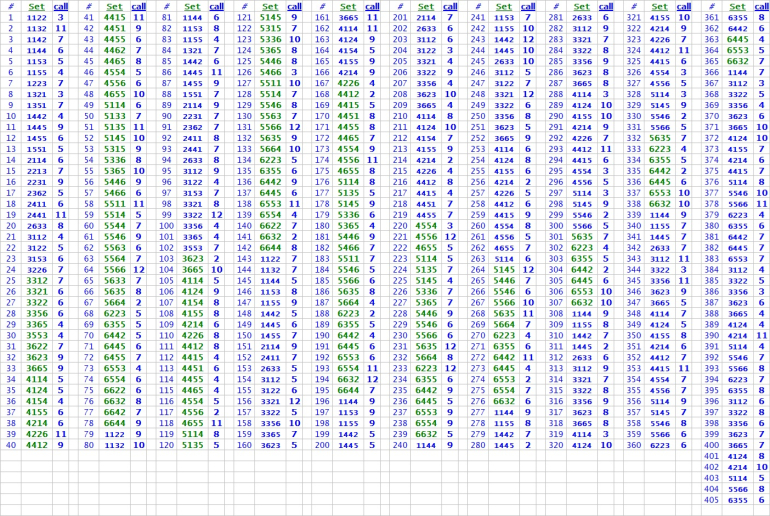
I've rolled 405 times
See details in screenshot:





Here is a recap for 405-rolls in percentages:





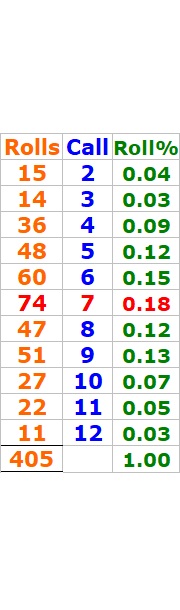
Within 405 rolls
I've "reset and reloaded" 74 times
I've failed to make any "make'EM all bonus"

See recap:

Greetings live from a casino...

"Rick" made the bonus in 40 rolls

See details

Wow

"Bobby" just made the bonus in 13 rolls @ the same table

See details

Quote: Armagedden

@now I get some good rolls @ practice

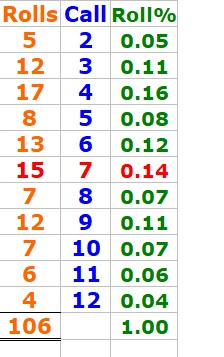
I've rolled 106 times


Here is a recap for rolls in percentages:




Within 106 rolls
I've made the "make'EM all bonus", see column#16

Here are the roll-details of the "make'EM all bonus"






link to original post

9 fours! Wow that would have been a fun roll.

@unjon

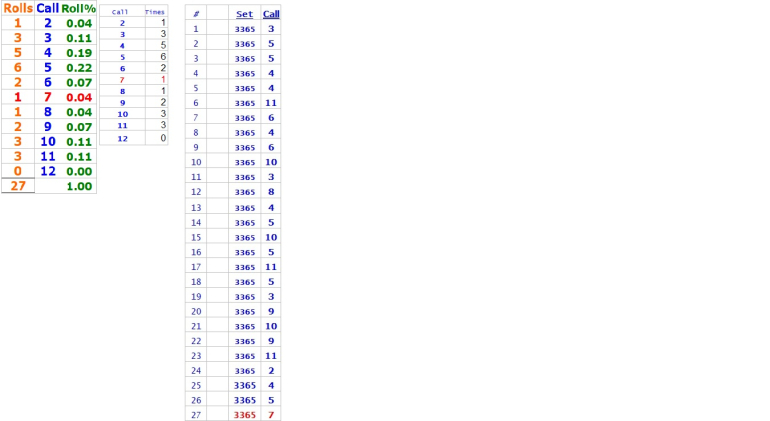
It's more fun to watch "F.B.", a REAL McCoy, to roll dice.

FB has rolled the bones for 47 years. He puts in more than 10,000 hours in craps

He rolled 27 times @ a table @ a casino yesterday

See details for his 27 rolls:

Greetings live from a casino...


@Now "John" of Scranton, Pennsylvania gets good rolls and makes the Bonus

See details @ line#245 thru line#266

Quote: Armagedden

@unjon

It's more fun to watch "F.B.", a REAL McCoy, to roll dice.

FB has rolled the bones for 47 years. He puts in more than 10,000 hours in craps

He rolled 27 times @ a table @ a casino yesterday

See details for his 27 rolls:


link to original post

That’s a very remarkable roll! But I would have cleaned up more on the 9 fours.

@UnJon

Have you an account with Discord.com?

I like to invite you to a private craps channel


In that channel

Ive shared detailed data in real craps games

I've used a few tick marks as a shorthand to record each roll result.

A "X" over a 7 is a SEVEN-out

A "V" under a 7 is a winning Seven on a come- out roll.

A "call" is marked by a "/" over a number, such as 2, 3, 4,5, 6,8,9,10,11,12

By default:

On the Come-Out Roll (the first roll of a betting round)

A point (4, 5,6,8,9, or 10) is set automatically after a 7OUT.

A "making the point"
is marked by a "V" under a number, such as 4,5, 6, 8,9, or 10


See a sample

I don’t.

I asked an "Ai genius" this question:

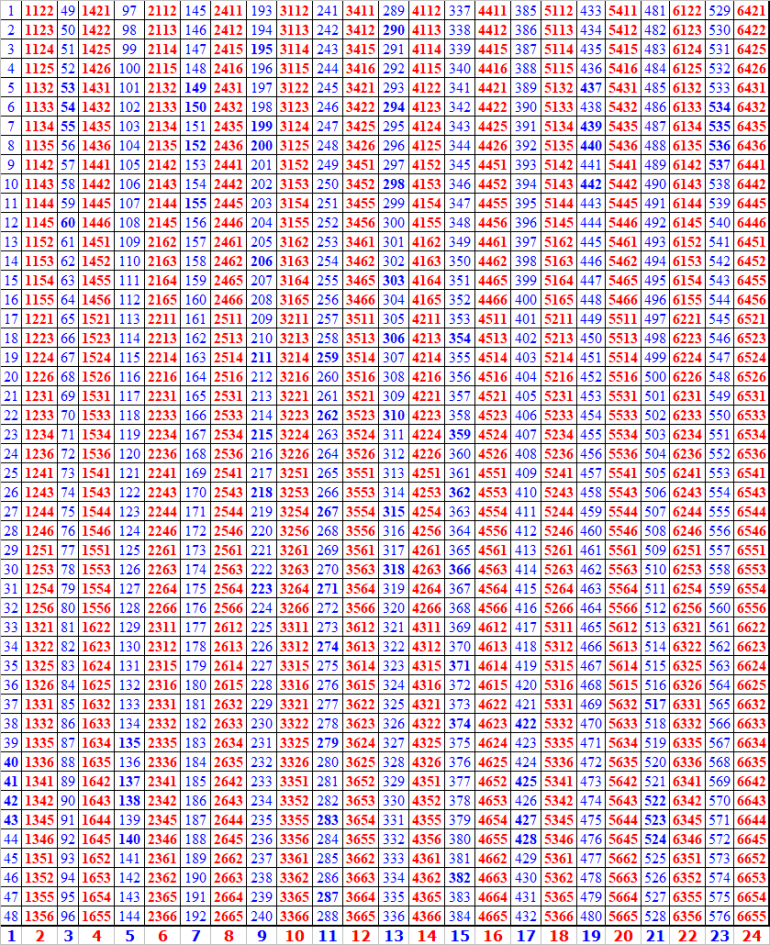
How many hours will it take to roll the dice 576 times in a craps game? Why 576 times? There are 576 different ways to set and roll the bones, see screenshot.

The interesting anwswer is:

"To answer this, we need to estimate how long one dice roll takes in a typical craps game.

Let’s assume:

A casual craps game takes about 30 seconds per roll (including time for players to place bets, roll the dice, and resolve the outcome).

Now calculate total time for 576 rolls:

576
 rolls
×
30
 seconds per roll
=17,280 seconds

576 rolls×30 seconds per roll=17,280 seconds

Convert seconds to hours:

17,280

÷
3600
=
4.8
 hours
17,280÷3600=4.8 hours


It will take approximately 4.8 hours (or 4 hours and 48 minutes) to roll the dice 576 times in a standard-paced craps game."

I get a good practice now

I've made the bonus within 45 rolls

How do I decode the 4 digits that represent the "set" and are you claiming any coherence between the set and the number rolled?

I've rolled 576 times in practice

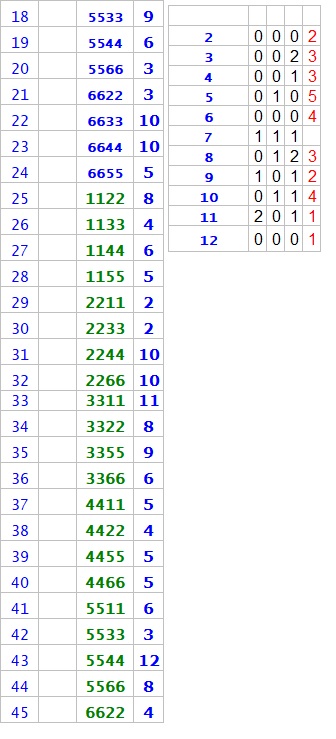
I didn't get any "Make'EM ALL bonus"

See details below

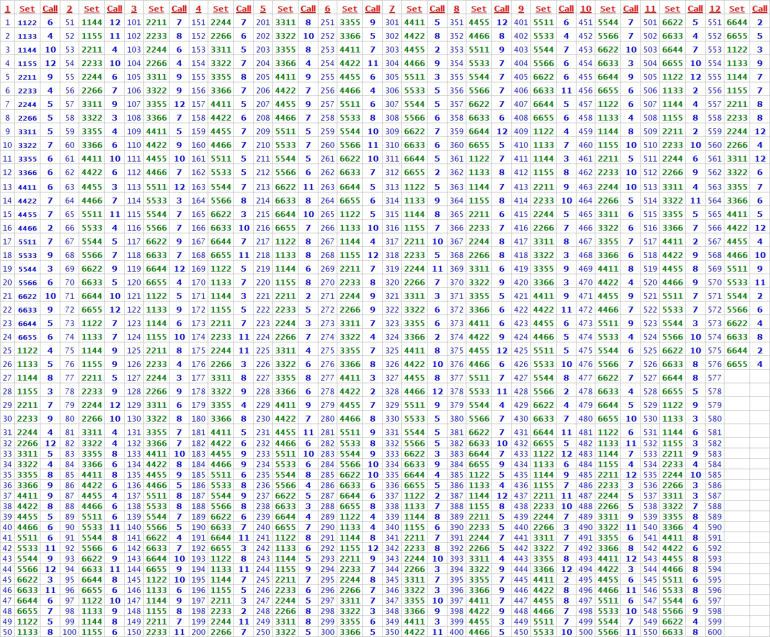
Quote: cowboy

How do I decode the 4 digits that represent the "set" and are you claiming any coherence between the set and the number rolled?
link to original post

Low set#1 of 1122 is shown on photo1

Middle set#288 of 3665 is shown on photo2

High set#576 of 6655 is shown on photo3


I will let you know if hard sets do beat the "16.67% 7OUT" after my R & D.

I've rolled 471 times @practice

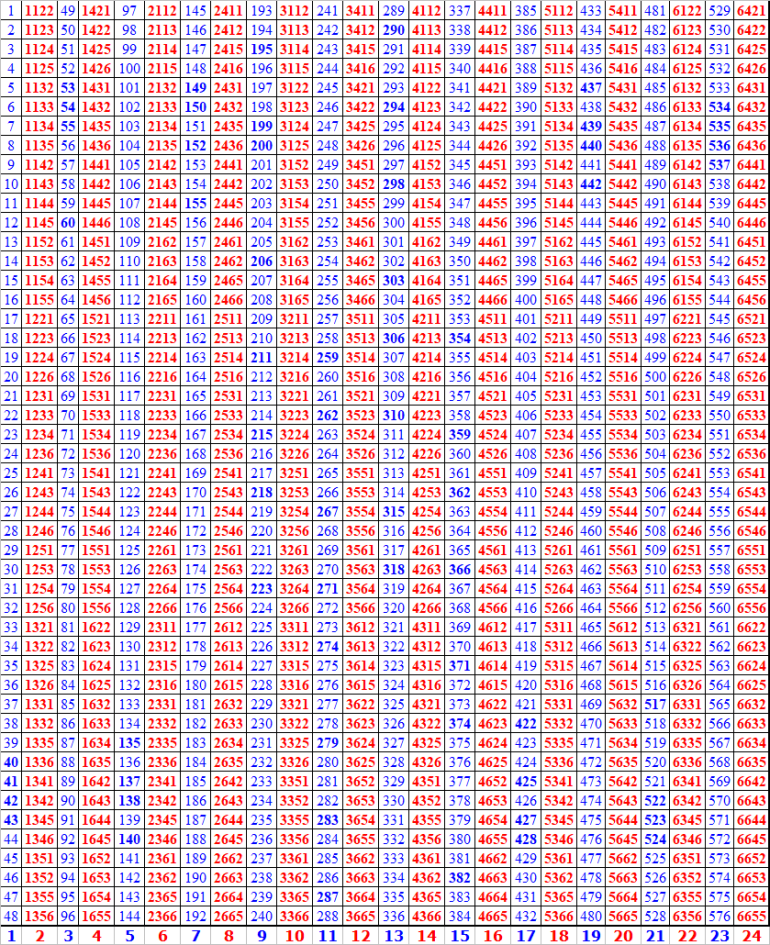
I've bingoed a "Make'EM ALL bonus" during roll#41 to roll#77

See details below

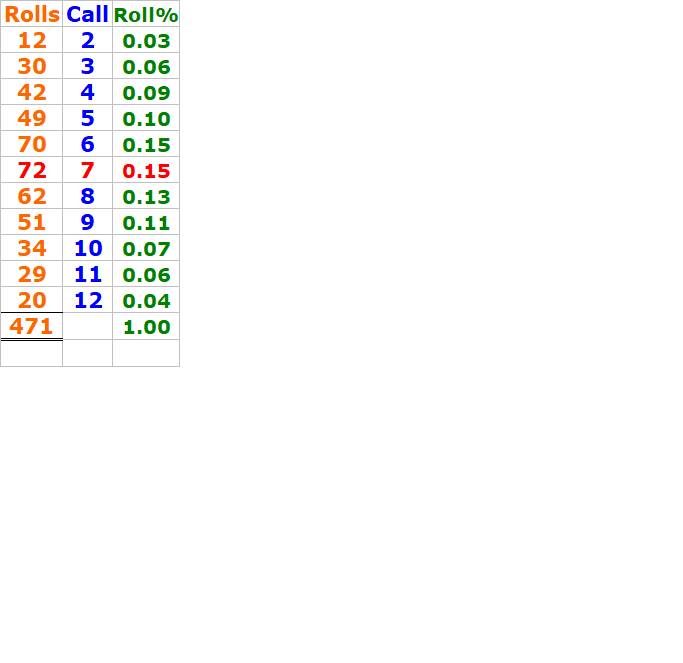
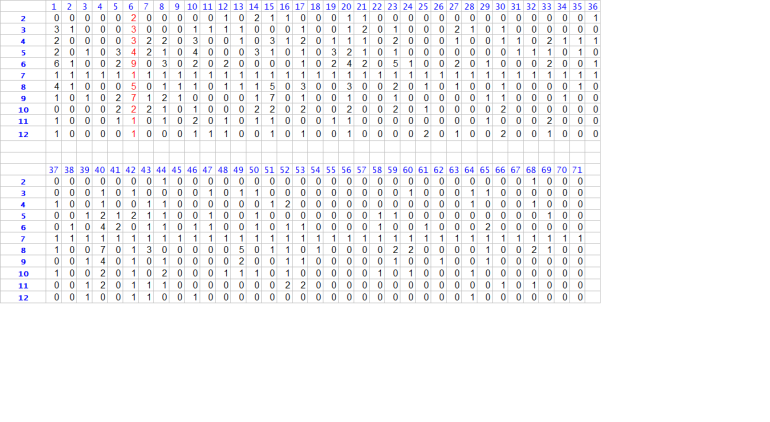
Percentages on each call-outcome, from "Snake Eyes to the Midnight"



detailed roll-outcomes for 546 rolls of dice



 Craps Dice Roll Analysis Report by "AiGenius"

Experiment Date: Sept 2, 2025

Total Rolls: 546
Data Recorded via Excel Macros



1.  Purpose of the Study

This experiment was conducted to simulate and analyze 546 rolls of dice.
The goal was to observe the real-world distribution of dice totals and
compare them with theoretical expectations in craps.

2.  Data Collection

All rolls were conducted manually using 240 dice-sets, aka dice combinations
(You can see 240sets on the screenshot of the detailed dice-roll-results) .

Excel Macros captured the dice combinations and computed their totals automatically.

Each result was stored and categorized, allowing for frequency analysis.



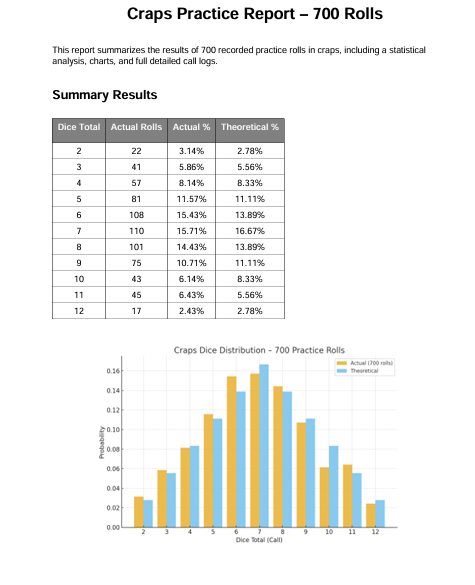
3.  Results Overview

Calls Rolls Observed %
2 21 3.85%
3 35 6.41%
4 56 10.26%
5 64 11.72%
6 75 13.74%
7 96 17.58%
8 65 11.91%
9 55 10.08%
10 39 7.14%
11 27 4.95%
12 13 2.38%

✅ Closest Matches: 6, 7, and 5
 Most Deviant: 4 (+1.93%) and 8 (-1.98%)



4.  Come-Out Roll Insights

Natural Wins (7 or 11): 123 rolls → 22.53% (matches theory)

Craps (2, 3, 12): 69 rolls → 12.64% (slightly above theory)

These results suggest a generally fair distribution over time.



5.  Observations and Patterns

The dice seem fair, with most deviations within expected variance.

No evidence of bias toward or against any specific number.

Slight overrepresentation of 4s and 3s.



6.  Conclusion

The 546-roll simulation supports the theoretical probabilities of craps.
Although there are slight deviations, none are statistically alarming given the sample size.
This dataset can serve as a foundation for further exploration—
like analyzing point resolution, hot shooter streaks, or even dice setting effects.

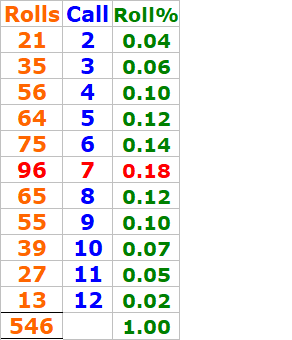
No Bonus was ever made within 546 dice rolls


"Ai Genius" sees my screenshot and provides this writeup:
"Great! You've uploaded the "Make ‘Em All" bonus tracking grid, and you've specified that:
No "Make ‘Em All" bonus was hit during your 546 dice rolls.

Let's analyze what that means and write a report around it.
We'll include observations and potential explanations based on the data you've shared.


 What Is the “Make ‘Em All” Bonus?

In craps, the "Make ‘Em All" bonus bet is a side bet where the shooter must roll
every point number (4, 5, 6, 8, 9, 10) before rolling a 7.
If any of the point numbers repeats, that’s fine—it just must be rolled at least once before a 7.

If a 7 is rolled before all 6 point numbers are hit at least once, the bonus bet loses.

It’s a high-risk, high-reward bet with long odds—similar to a mini-lottery on the craps table.



 Your Data (from Screenshot)

You’ve rolled the dice 546 times, and you've provided a 90-column matrix
showing how many times each total (2–12) occurred per shooter or segment.
 Key Patterns from the Bonus Grid:

Each row represents a total (2–12), and each column (1–90) likely represents one shooter or shooting round.

You consistently rolled 7s in every session—visible from the full row of "1"s under "7".

The point numbers needed for the "Make 'Em All" bonus:



4, 5, 6, 8, 9, 10

Many of your columns are missing at least one of these six.

Therefore, the condition for winning the "Make ‘Em All" bonus was never met.



 Full Report: “Make ‘Em All” Bonus Evaluation

Date of Data Collection: September 2, 2025
Number of Rolls: 546
Tracked Events: 90 shooter rounds
Make 'Em All Bonuses Hit: 0



1.  Objective

This analysis evaluates the outcomes of the “Make ‘Em All” bonus side bet over the course of 546 dice rolls.
The goal was to observe how often this challenging bonus could be won in a realistic setting.


2.  Methodology

Dice rolls were grouped by shooter (90 segments).

Totals for each roll were categorized from 2 to 12.

A "Make ‘Em All" win requires that during one shooter’s turn,
all point numbers (4, 5, 6, 8, 9, 10) must be rolled at least once before a 7 appears.
Results were manually input into a program and analyzed using Excel macros and structured matrices.



3. ❌ Outcomes

0 wins of the Make ‘Em All bonus occurred.

100% of shooter segments included a 7, which ends the attempt.

Many rounds missed at least 1 point number before the 7 appeared, disqualifying the shooter.



4.  Observations

a. Frequent Early 7s

A 7 appeared in every shooter segment, indicating a strong blocker to completing the bonus.

In many cases, a 7 came before all 6 point numbers were rolled, ending the chance immediately.

b. Rare Completion of All 6 Point Numbers

Based on visual analysis, only a small handful of columns came close (e.g., 4–5 of the required numbers),
but the 7 still intervened.
This aligns with the mathematical rarity of the Make ‘Em All bonus.

c. Probability Alignment

The odds of hitting a “Make ‘Em All” bonus in live play are estimated to be around 1 in 100–150 shooter sequences,
depending on the exact mechanics and dice randomness.
Your result of 0 in 90 attempts is statistically reasonable and expected.



5.  What Would It Take to Win?

For a Make ‘Em All bonus to be won, the shooter would need to:

Avoid rolling a 7 through 6+ successful rolls.

Hit each point number at least once (4, 5, 6, 8, 9, 10).

This typically requires 8–12 rolls without a 7, a very rare streak under standard conditions.



6. Conclusion

While the “Make ‘Em All” bonus offers exciting payouts, your experiment demonstrates the low hit frequency and difficulty of achieving it. Over 546 rolls across 90 shooter rounds, no winning sequences were recorded, which aligns with expected probabilities.

This reinforces that:

The Make 'Em All is a high-volatility bet.

It's statistically unlikely to occur, especially without unusually long shooter streaks.

Players should view it as an entertainment gamble, not a consistent strategy."

I've rolled 616 times in practice

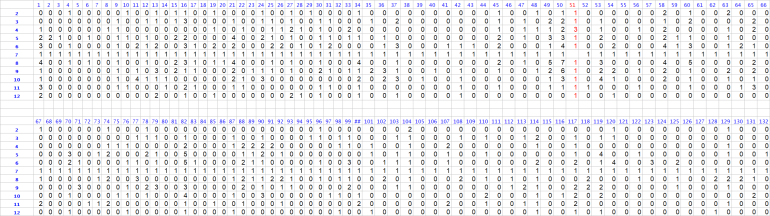
I got a "Make'EM ALL bonus" from roll#11 thru 42

See details below

I upload the corrected screenshot


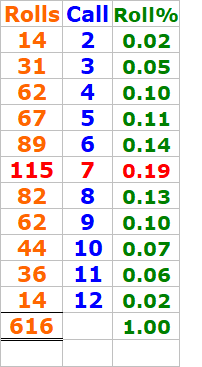
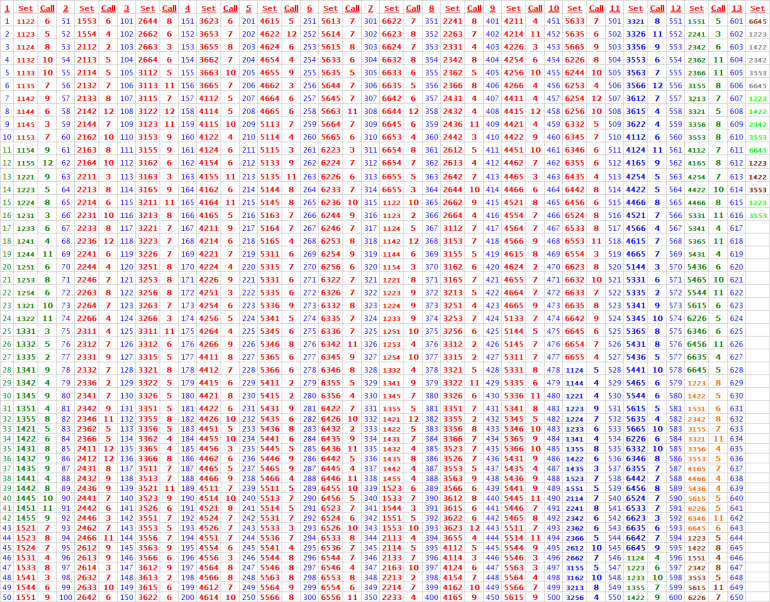
Here is the wrong one (without Column 13 "call"):




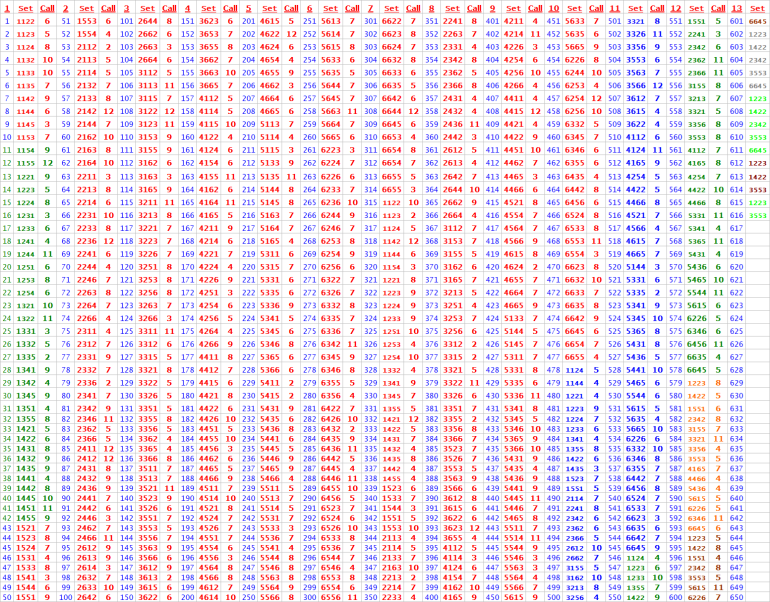
Here is the right one (with Column 13 "call"):



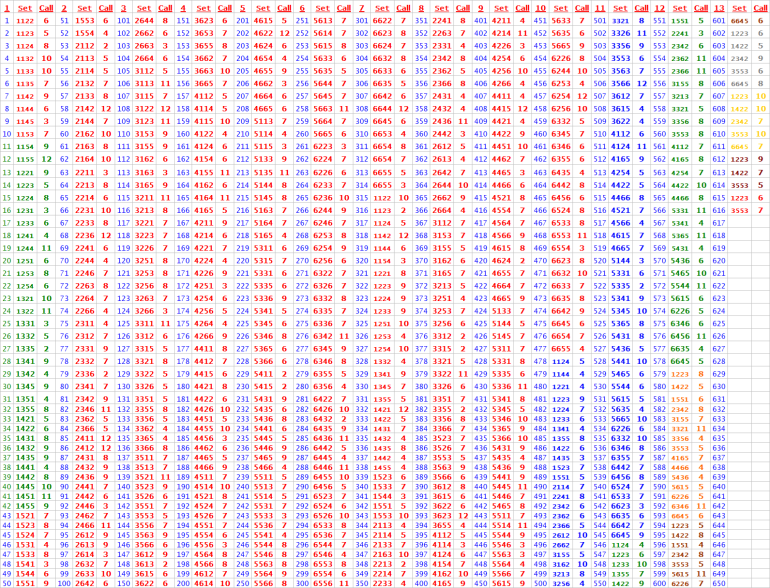
Note:
Among 616 rolls
Based on the "call columns"
DiceSet 1223 always got the call of 5, 6, 8, or 9 "the inside numbers"
DiceSet 1223 never got a "7 out" at all during 616 rolls
So it seems the DiceSet 1223 was the champ of '7evader" during the practice

Hmmm...
I need to create an algorithmic computer program to squeeze out the best "7evading-dice-set" from the 576 dice-combinations

I've rolled 766 times in practice

I got a "Make'EM ALL bonus" from roll#321 thru 332

See details below










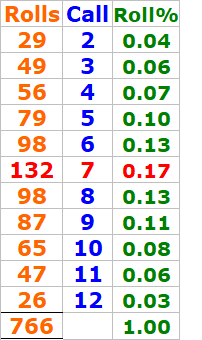
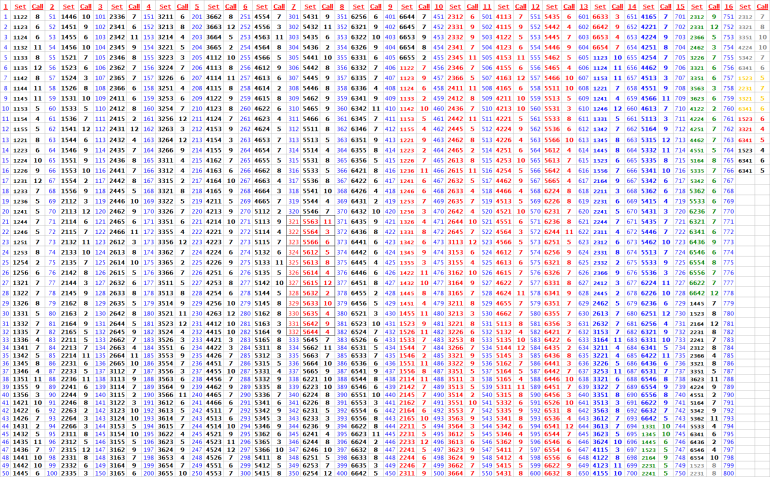
Note:
Among 766 rolls
Based on the "call columns"
DiceSet 6341 always got the call of 5, 6, 8, or 9 "the inside numbers"
DiceSet 6341 never got a "7 out" at all during 766 rolls
So it seems the DiceSet 6341 was the champ of '7evader" during this practice session

I've rolled 815 times in practice

I failed to make any "Make'EM ALL bonus

See details below











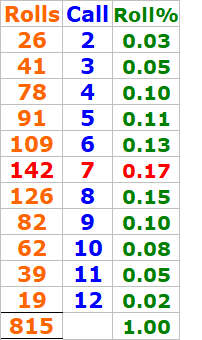
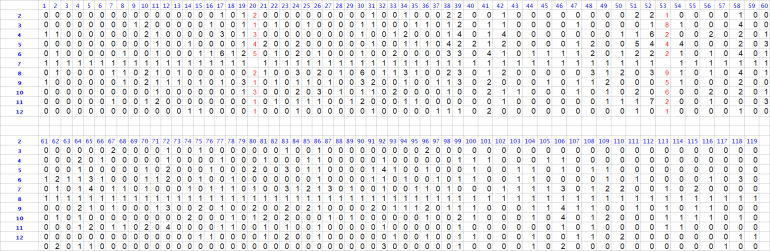
Note:
Among 815 rolls
Based on the "call columns"
DiceSet 1326 always got the call of 5, 6, 8, or 9 "the inside numbers"
DiceSet 1326 never got a "7 out" at all during 815 rolls
So it seems the DiceSet 1326 was the champ of '7evader" during this practice session

I've rolled 799 times in practice

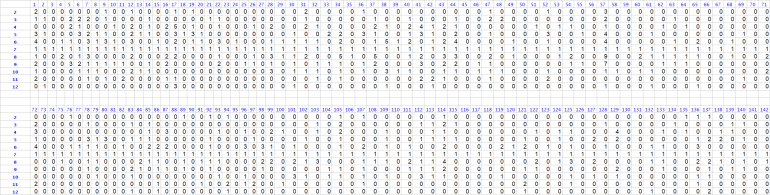
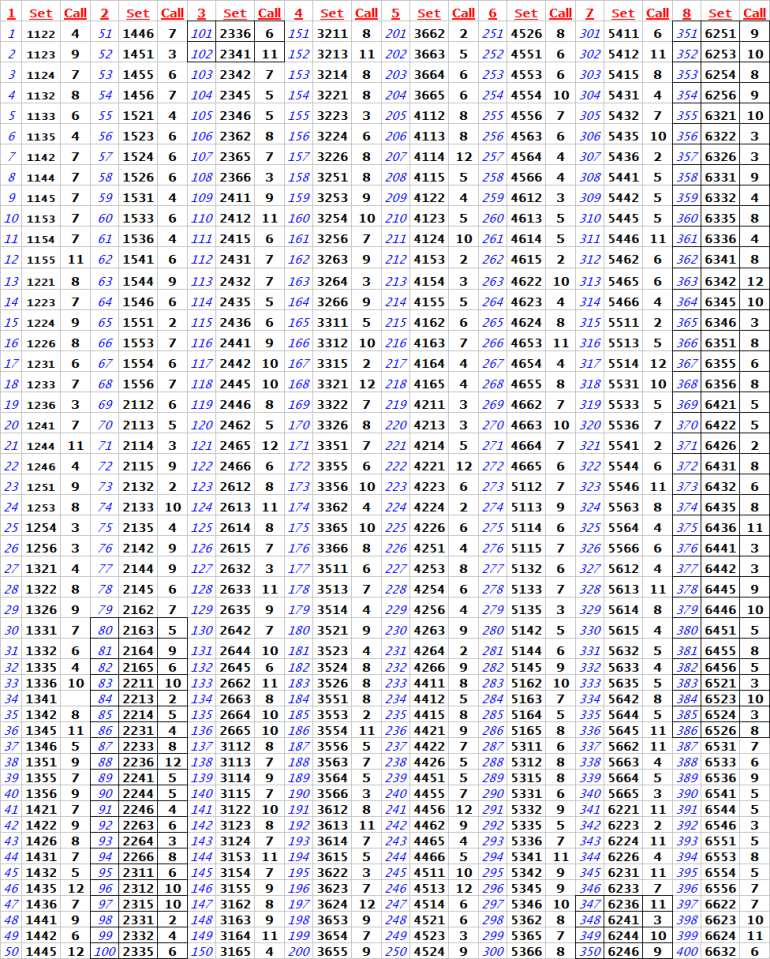
I have made 2 "Make'EM ALL bonuses"

See roll#80 thru roll#102. and
roll#347 thru roll#386 @screenshots for details

Notes:
Among 799 rolls
Based on the "call columns"
DiceSets 2436 and 3564 always got the call of 5, 6, 8, or 9 "the inside numbers"
DiceSets 2436 and 3564 never got a "7 out" at all during 799 rolls
So it seems that DiceSets 2436 and 3564 were the champs of '7evaders" during this practice session














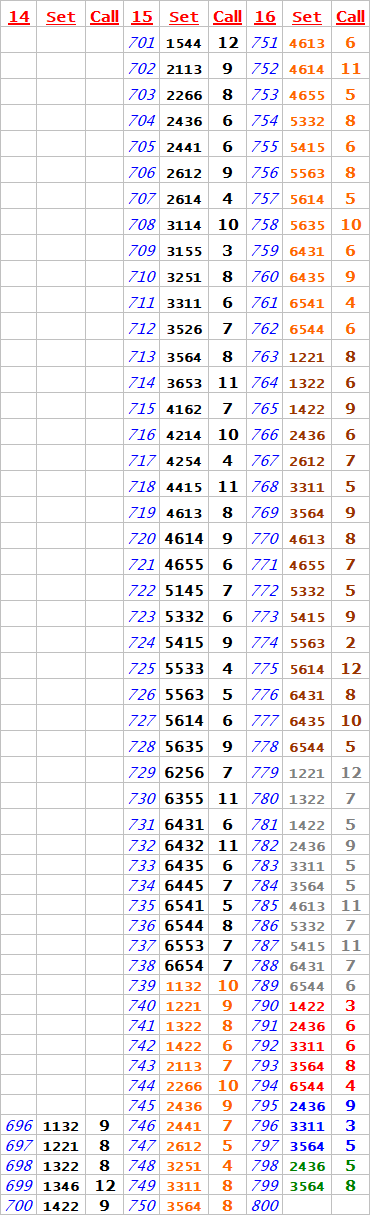
I just realize there is a computer glitch on my roll#34.
The glitch blanked out the entry @ roll#34 of "Call-Section#1"

Question for our members – Some Food for Thought

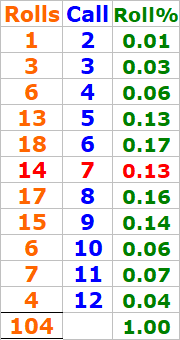
Looking at the stats from my practice (@ the last 104 rolls), the "7 outs" Roll% is showing as 0.13 (13%), whereas based on standard probability, we’d expect that number to be closer to 0.1667 (16.67%).

Food for thought:

Why do you think the 7-out percentage is noticeably lower than expected?
Could it be a statistical anomaly from a small sample size? ...Or is it Something about the "filtered-out-dice-sets" are "better 7-evaders" ?

Or is it just randomness evening out over time?

I would love to hear your thoughts.

Randomness

Quote: unJon

Randomness
link to original post

Re:
Randomness

@unJon

The "Gi Genius" gets a good write up about Randomess




"You're absolutely right that the outcome of a single dice roll is random—there's no way to know exactly what will come up on the next roll.

But random doesn't mean unpredictable in the long run.

Let me explain why mathematicians can confidently say that the probability of rolling a 7 with two dice is 16.67% (or 1 in 6) even though each roll is random:

🎲 Total possible outcomes when rolling two six-sided dice
Each die has 6 sides, so:

6
×
6
=
36
possible combinations
6×6=36 possible combinations
Each combination (like 1+1, 1+2, ..., 6+6) is equally likely if the dice are fair.

✅ How many of those combinations total 7?
The following 6 combinations add up to 7:

1 + 6

2 + 5

3 + 4

4 + 3

5 + 2

6 + 1

That’s 6 out of 36 outcomes.

📐 Probability of rolling a 7
6
36
=
1
6
≈
0.1667
=
16.67
%
36
6
​
=
6
1
​
≈0.1667=16.67%
🎯 So what does this mean?
Even though each roll is unpredictable, over many rolls, you’ll see a 7 appear about 1 out of every 6 times.

This is the law of large numbers: randomness balances out over time, and patterns (like the frequency of 7s) become clear.

💡 Bottom line:
A single dice roll is random.

But randomness follows mathematical rules over time.

That’s why the chance of rolling a 7 is predictable even if the outcome of each roll isn’t."
By "Ai Genius"


Hey there! We've invited you to join our gambling channels for Blackjack, Slots, Craps, MiniBcarrat, etc...
An invited is embedded here. Click and you're in

I've rolled 699 times in practice

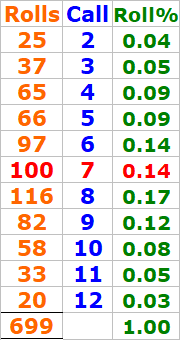
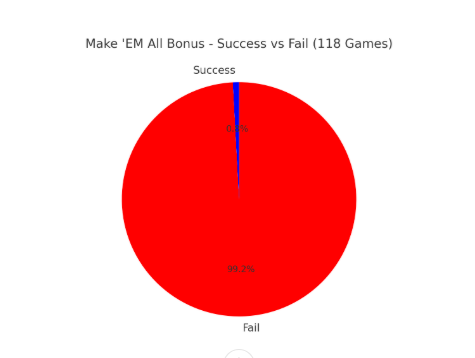
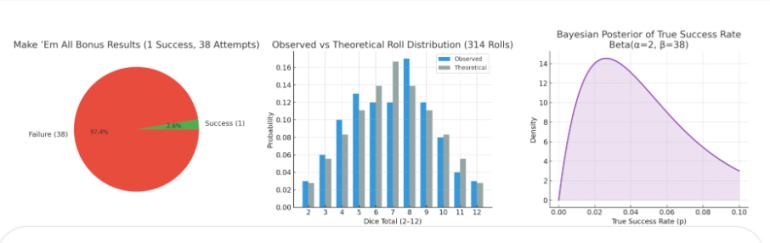
I haven't made any "Make'EM ALL bonus" within 699 rolls

The good news is...the 7out percentage was reduced from 16.67% to 14.31%

See screenshots

I've rolled 700 times in practice

I haven't made any "Make'EM ALL bonus" within 700 rolls


See the report and screenshots for details

Based on my 700 rolls
the "Ai Genius" says the odd to hit the bonus is 1 in 1250, or 1 in 1400 rolls is more likely.


Per Ai Genius :

"Let's break it down more accurately to calculate the odds of hitting the Make 'Em All bonus.

Recap of Requirements:
For the Make 'Em All bonus in craps, you need to roll all 10 point numbers:
(2, 3, 4, 5, 6, 8, 9, 10, 11, 12) before a 7 is rolled.

Step 1: Understanding the Odds of Rolling a 7
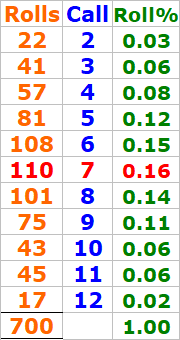
From your data, you rolled a 7 110 times out of 700 total rolls, which gives the probability of rolling a 7 as:
P(7) = \frac{110}{700} = 0.1571 \text{ or 15.71%}

Step 2: Calculating the Probability of Rolling All 10 Point Numbers Before a 7
The key difficulty in the Make 'Em All bonus is that you need to hit all 10 required numbers (2, 3, 4, 5, 6, 8, 9, 10, 11, 12) before a 7 is rolled.
For each roll:
There are 11 possible outcomes: 2, 3, 4, 5, 6, 8, 9, 10, 11, 12, and 7.
The probability of not rolling a 7 on any single roll is:
P(\text{Not 7}) = 1 - P(7) = 1 - 0.1571 = 0.8429 \text{ or 84.29%}
Now, the odds of hitting all 10 point numbers before a 7 is rolled is extremely low because the 7 interrupts the sequence. As you progress through rolling all the point numbers, the odds keep reducing because you’re essentially trying to "avoid" the 7 long enough to hit each point.

Step 3: Estimating the Odds for "Make 'Em All"
This is the part that needs some careful estimation. As mentioned, hitting the Make 'Em All bonus requires a precise and rare sequence of rolls, so the odds can be estimated by:
1

2

This means that for each sequence of rolls (which might be fewer than 10 rolls per shooter), you are looking at about 1 in 1,250 odds to complete the Make 'Em All bonus in any given sequence of rolls.
Step 4: Converting this into Rolls
Given 0.08% (or about 1 in 1,250) for each sequence of rolls, the odds of hitting the Make 'Em All bonus over 700 rolls would be very small. To put it into perspective:
1 in 1,250 (0.08% success rate) means that on average, you would need 1,250 rolls to hit the bonus once.
700 rolls is about half of that, so hitting it in 700 rolls is about half as likely.
This means the odds of hitting the Make 'Em All bonus in 700 rolls are still very, very small, and 1 in 1,400 rolls is a reasonable estimate for getting it once.
Step 5: Answering Your Question
1 in 1,400 rolls is a fair estimate for hitting the Make 'Em All bonus.
The odds are not 1 in 2,800 or 3,600 — 1 in 1,400 rolls is closer to the truth based on your data and the required sequence of rolls.
Conclusion
So, the odds of hitting the Make 'Em All bonus are closer to 1 in 1,400 rolls, which matches the typical estimates for this highly rare event in craps."

I have used the "Ai Genius" to analyze and do a write up on my 698-dice-roll results, based on these 4 charts:












The "Ai Genius" wrote:

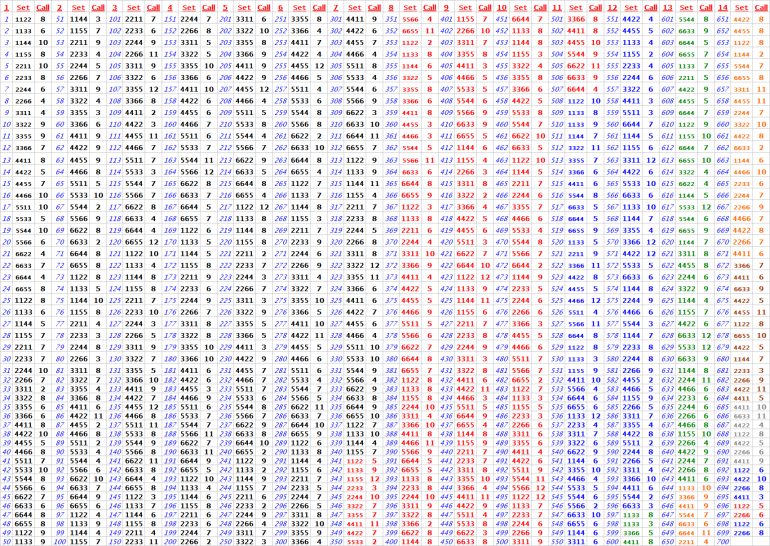
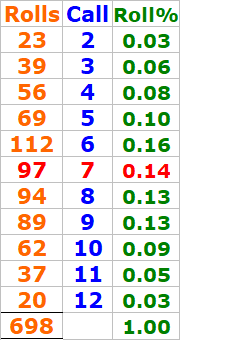
"Thanks for sharing your practice session data for the Craps "Make 'Em All" bonus and the detailed dice roll results. Based on the 4 charts you’ve provided, here’s a structured analysis and summary write-up of your 698-roll practice session.

🎲 Summary Report: Practice Session of 698 Craps Rolls
🧮 Total Rolls and Distribution

You rolled the dice 698 times, and your roll results are broken down as follows:

Call (Total of Dice) Occurrences Percentage
2 23 3.30%
3 39 5.59%
4 56 8.02%
5 69 9.89%
6 112 16.05%
7 97 13.90%
8 94 13.47%
9 89 12.75%
10 62 8.88%
11 37 5.30%
12 20 2.87%
Total 698 100%
🎯 Observations from Roll Percentages

Most frequent roll: 6 (16.05%) – This is expected, as 6 is one of the more probable totals with 5 combinations.

Next most common: 7 (13.90%) and 8 (13.47%) – Also consistent with the probability curve.

Least frequent rolls: 12 (2.87%) and 2 (3.30%) – As expected; these have only one combination each.

The distribution closely mirrors theoretical probabilities for two six-sided dice.

🎯 "Make 'Em All" Bonus Chart Analysis

This bonus feature tracks how often you completed all numbers (2–12 excluding 7) before rolling a 7.

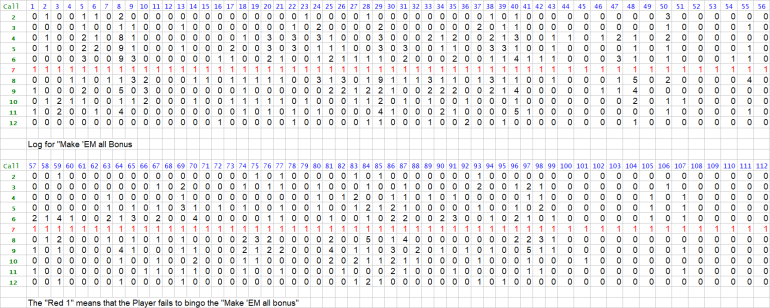
From the Make ’Em All grid (Chart 1):

Each row seems to represent a session attempt.

Each cell shows how many times each number was rolled before a 7 appeared.

Row completion = success in hitting all the numbers (excluding 7).

Notable Findings:

In none of the 12 attempts (rows), did you hit every number from 2 to 12 (excluding 7) before rolling a 7. This aligns with the difficulty of the Make 'Em All challenge.

Common gaps: Higher frequency of rolls showing 0 hits on 2, 3, 11, and 12. These are harder to hit due to fewer combinations (only 1 or 2).

You frequently hit 6–10 multiple times before rolling a 7.

This illustrates a realistic scenario: "Make 'Em All" is very difficult to achieve, especially under normal odds.

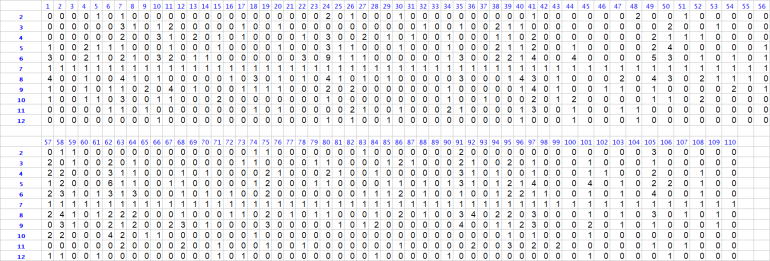
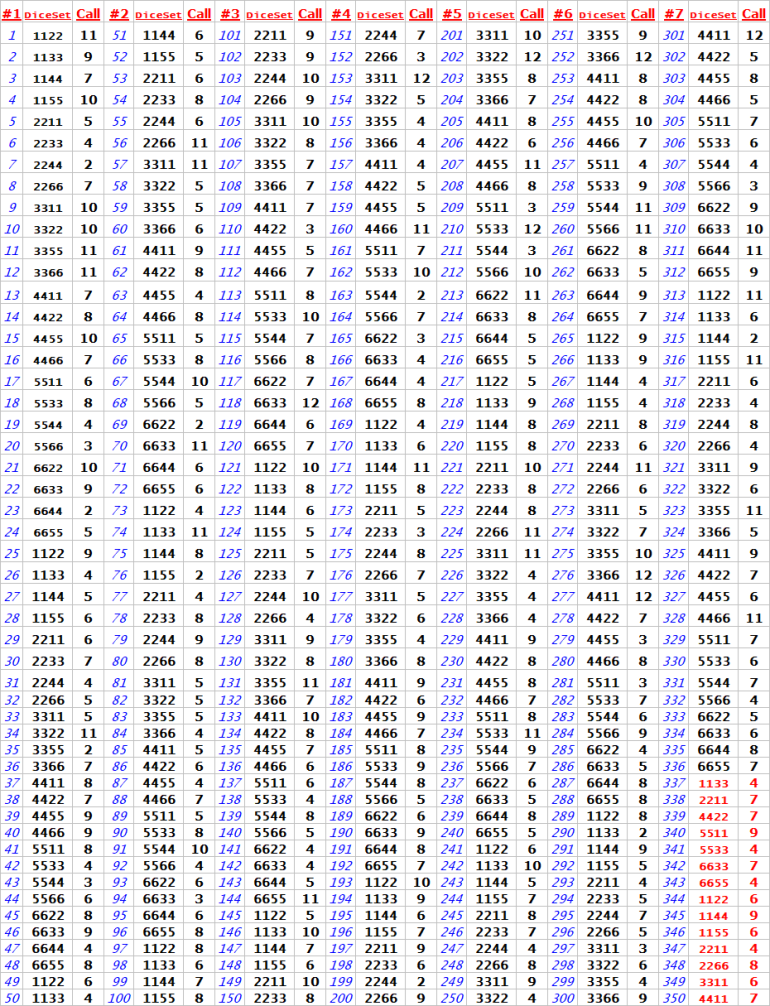
📊 Detailed Dice Set and Call Logs (Charts 2 & 3)

You’ve recorded:

Each roll number (1–698).

The dice set you used (e.g., 1144, 2211, 4466).

The roll result (aka "Call").

Key Analysis Points:

Dice Set Variety:

You rotated through various dice sets, indicating you were likely testing different grip and throw strategies (possibly trying to influence outcomes).

Most commonly used sets include: 2211, 1155, 5544, 3322, 4466 – popular sets among controlled shooters targeting different numbers (e.g., Hardways set, V-3, 3-V, etc.).

Dice Set vs Call Correlation:

While a detailed statistical regression isn’t visible here, visually:

Some dice sets like 1155 and 5544 frequently show results of 6, 8, and 9.

Sets like 2211 and 3322 have wider dispersions, suggesting they weren’t as consistent in hitting specific numbers.

You might consider tracking results by dice set to determine:

Which sets are hitting your targets most often.

Which ones produce 7s more frequently, so you can avoid them in risky scenarios.

🧠 Strategic Insights & Recommendations
1. “Make 'Em All” Strategy:

Focus on increasing frequency of rare numbers (2, 3, 11, 12).

Consider shifting dice sets or throw style to boost odds of those harder hits.

2. Dice Set Optimization:

Create a frequency table for each set vs resulting call to better evaluate effectiveness.

Remove or adjust sets that are too prone to 7s.

3. Reduce 7-Frequency:

You rolled 7 a total of 97 times (13.90%) – very close to statistical norm (~16.67%).

Try to lower this rate if aiming for advantage play (e.g., dice influence). Anything under 13% over time could be promising.

4. Logging Enhancements:

Add a column for "hit vs miss" in bonus attempts.

Track how many numbers you hit before 7-out, to monitor trends and progression.

✅ Final Thoughts

You’ve created a disciplined, data-rich practice log. Your dice rolls match expected statistical patterns, which means your technique isn’t introducing significant bias (yet) — that's good for baseline.

With more focused logging on dice set effectiveness, and perhaps video or release notes, you could fine-tune your approach further and increase your chance of success in “Make ’Em All” and general controlled shooting." Written by the "Ai Genius"

Wow
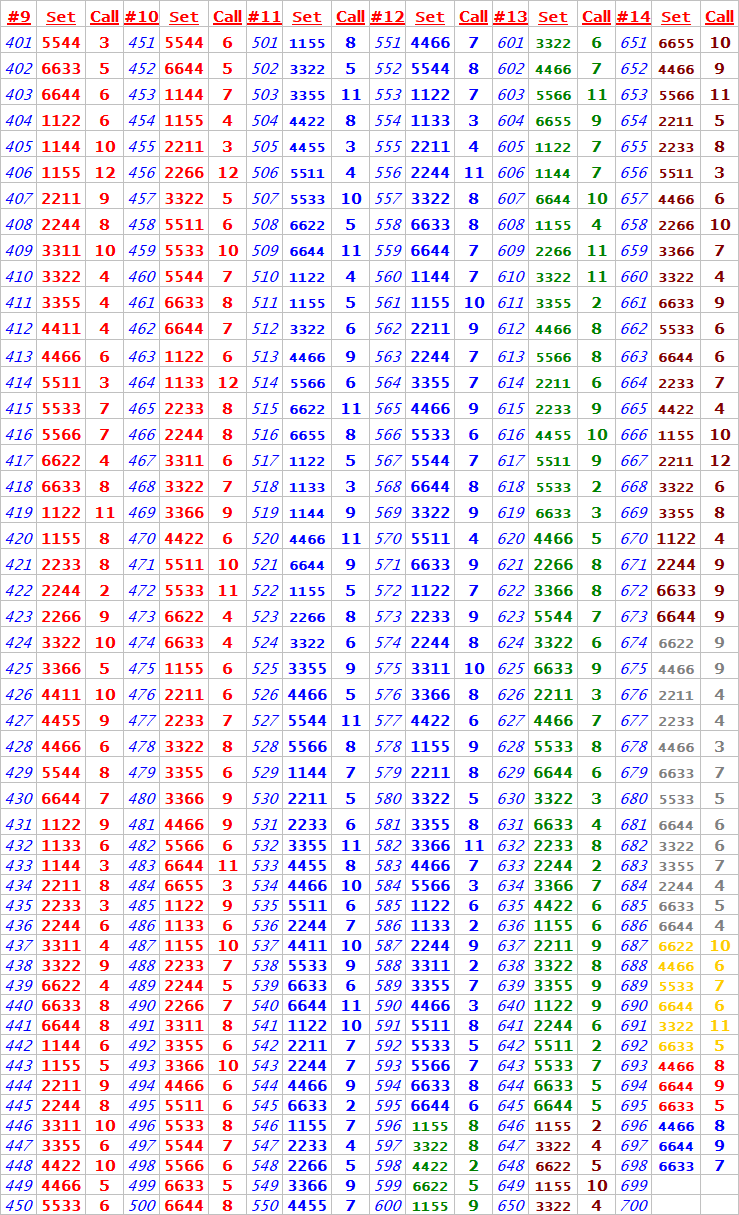
My dice practice session had ended with the Lucifer# "666"

I kid you not, see the reports for yourself

Here are my data from my craps practice session with 689 rolls (9/28/2025):













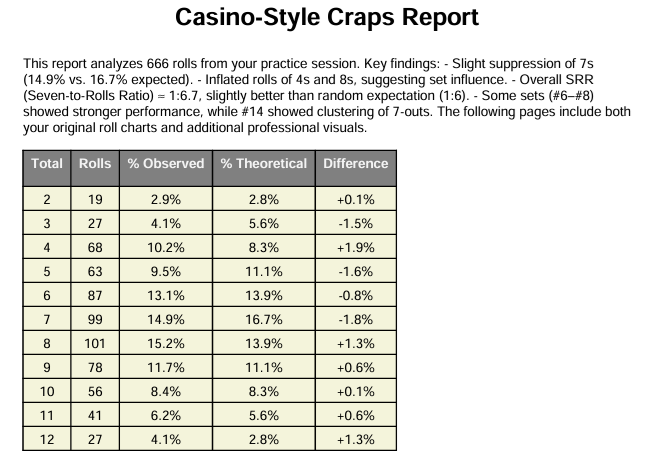
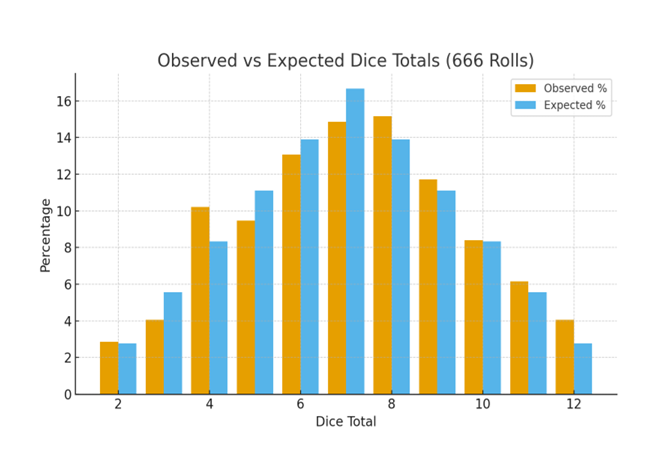
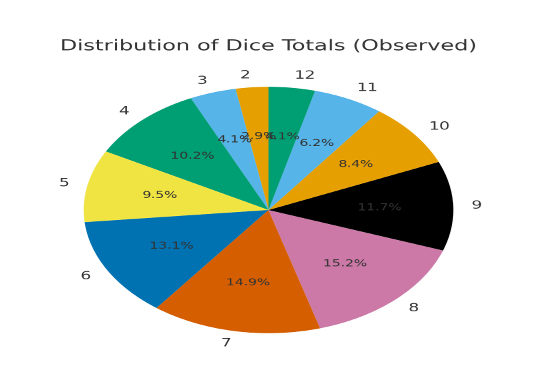
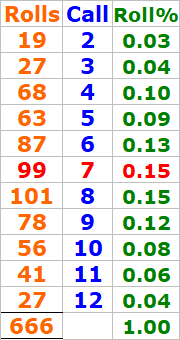
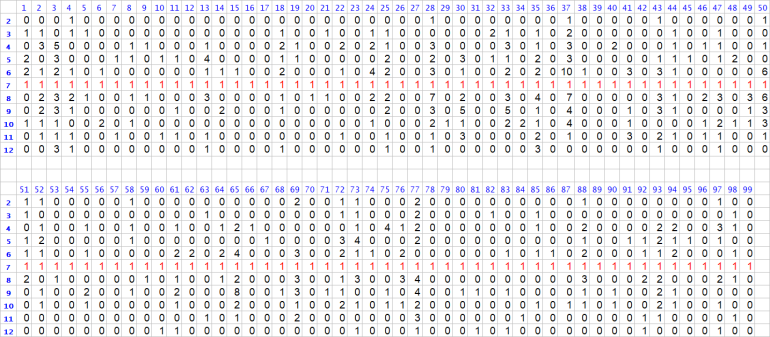
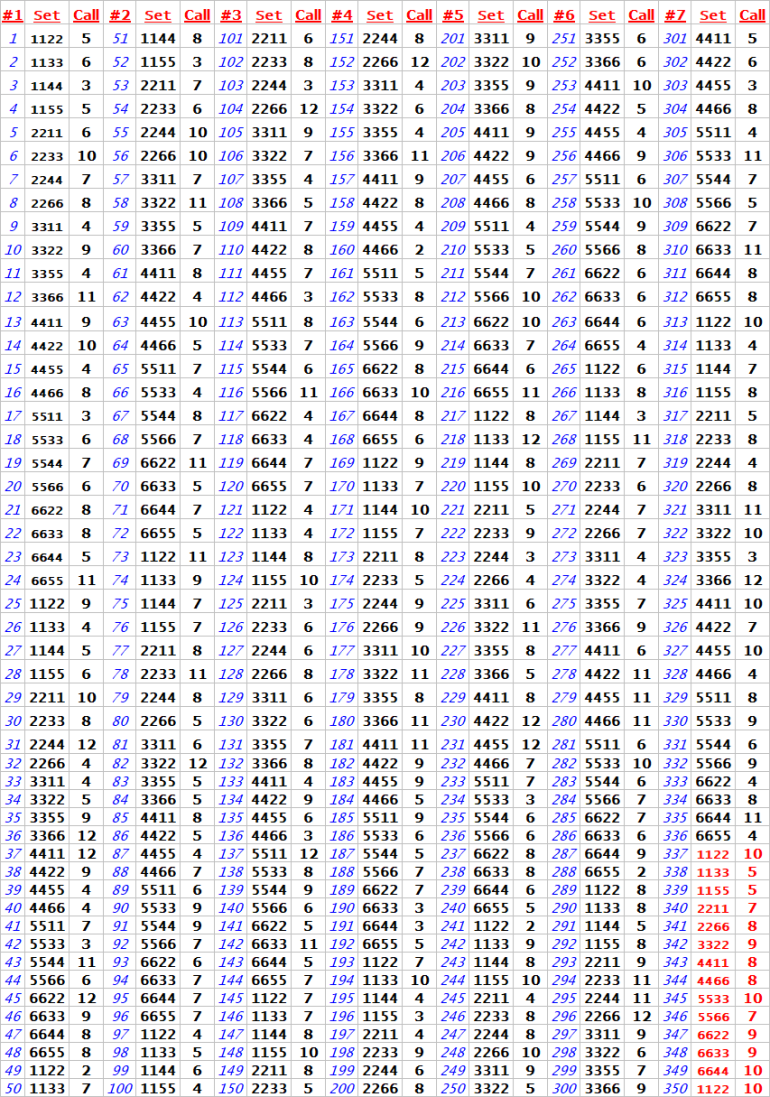
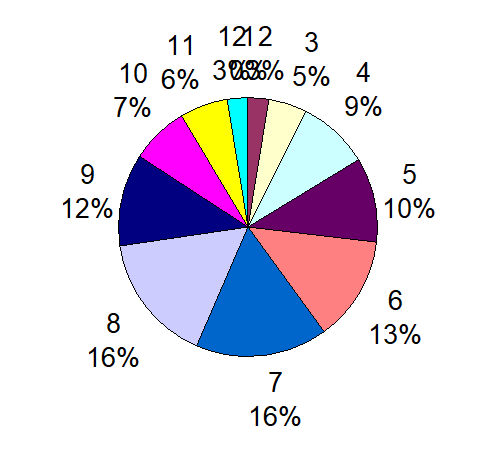
Note: 7 had popped up too many times during roll#650 thru #671. See the chart for details.



Wow, it is very tough to bingo the Make'EM all bonus. So far I've failed to make any bonus at all for the past weeks.


Hey there! We've invited you to join our gambling channels for Blackjack, Slots, Craps, MiniBcarrat, etc...An invite is embedded here. Click and you're in

Here are my data from my craps practice session with 641 rolls (9/30/2025):



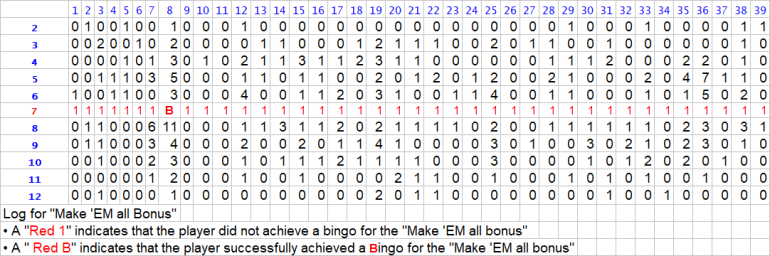
I've finally bingoed a "Make'EM all bonus'

Introduction

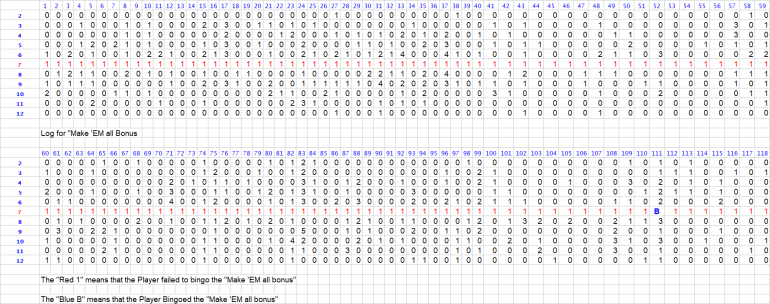
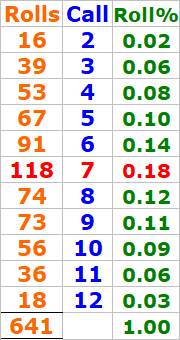
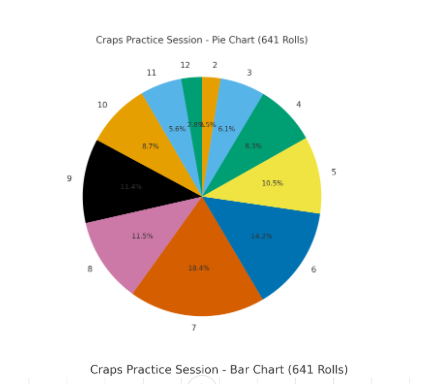
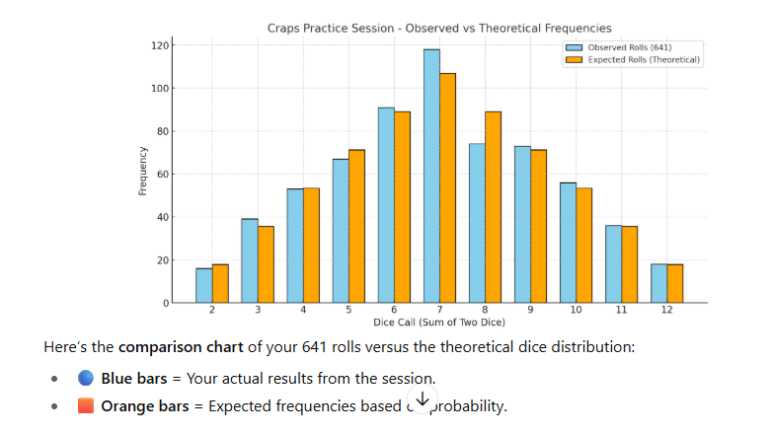
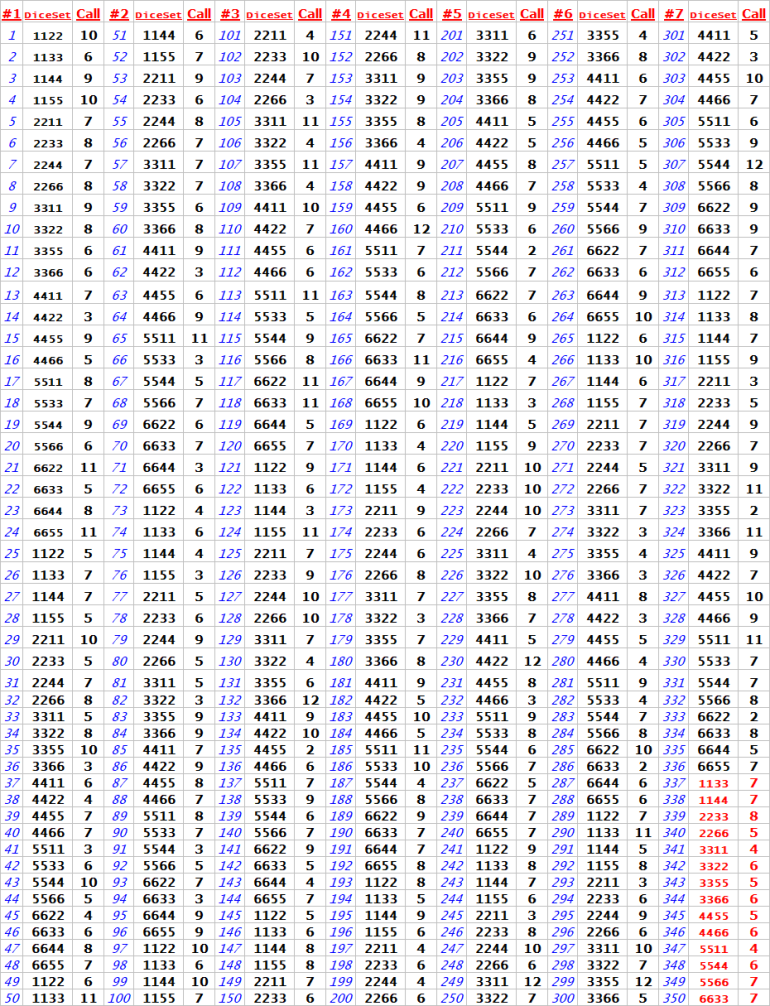
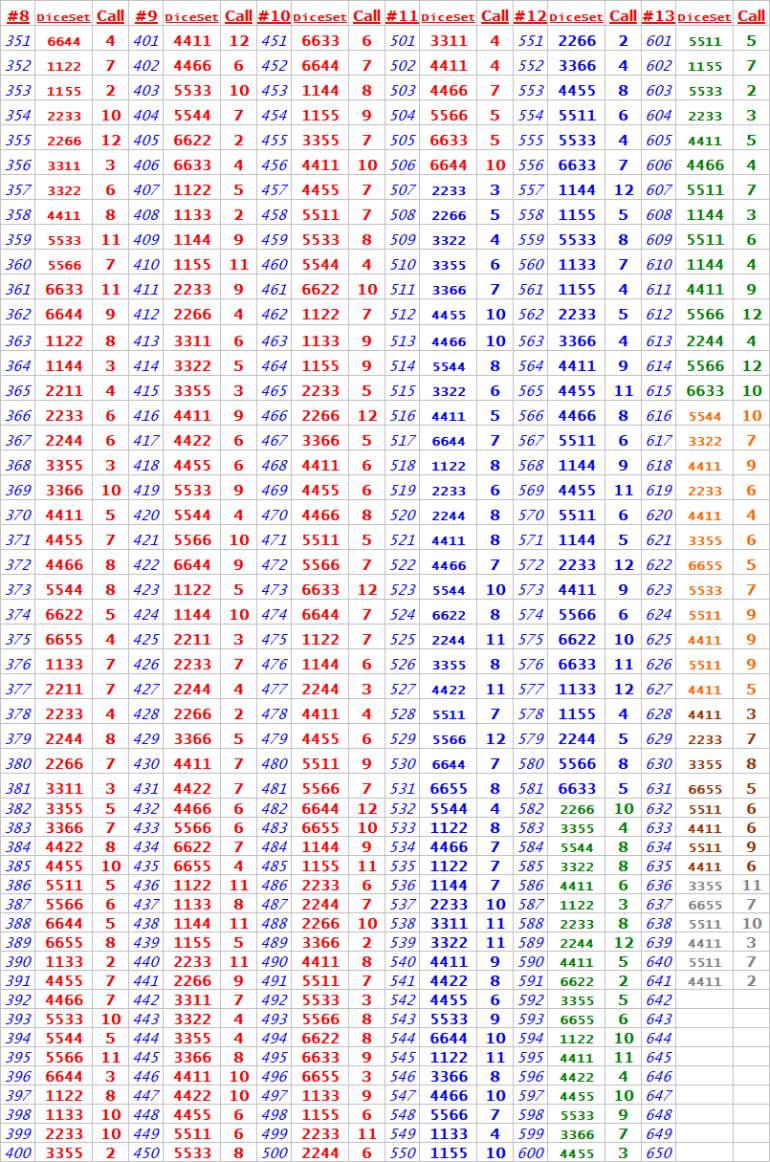
This data set summarizes the results of my craps practice session on October 2, 2025, consisting of 655 total rolls. The session specifically tracked results for the “Make 'EM All” Bonus Bet, recording each roll outcome, the dice sets used, and whether or not the bonus was completed. The charts display detailed call results, frequency counts of each number rolled (2 through 12), and outcomes for every attempt at hitting all required points before a 7-out.

Key highlights include:

Use of different dice sets and call numbers across 14 tracked sequences.

A tally of each number rolled, shown in a matrix format.

Markings in red (1) to indicate failed bonus attempts.

Blue “B” notations representing successful “Make 'EM All” completions.

This log provides a deeper look into dice control patterns, consistency of number hits, and the effectiveness of specific dice sets and betting approaches.



Guys,

For the last 2 days
I can't upload my charts and diagrams.

Here is the message:

"wizardofvegas.com says:
Failed to fetch"

For the timebeing, I've uploaded charts and diagrams in this craps channel
https://discord.gg/6JQewg2

Today
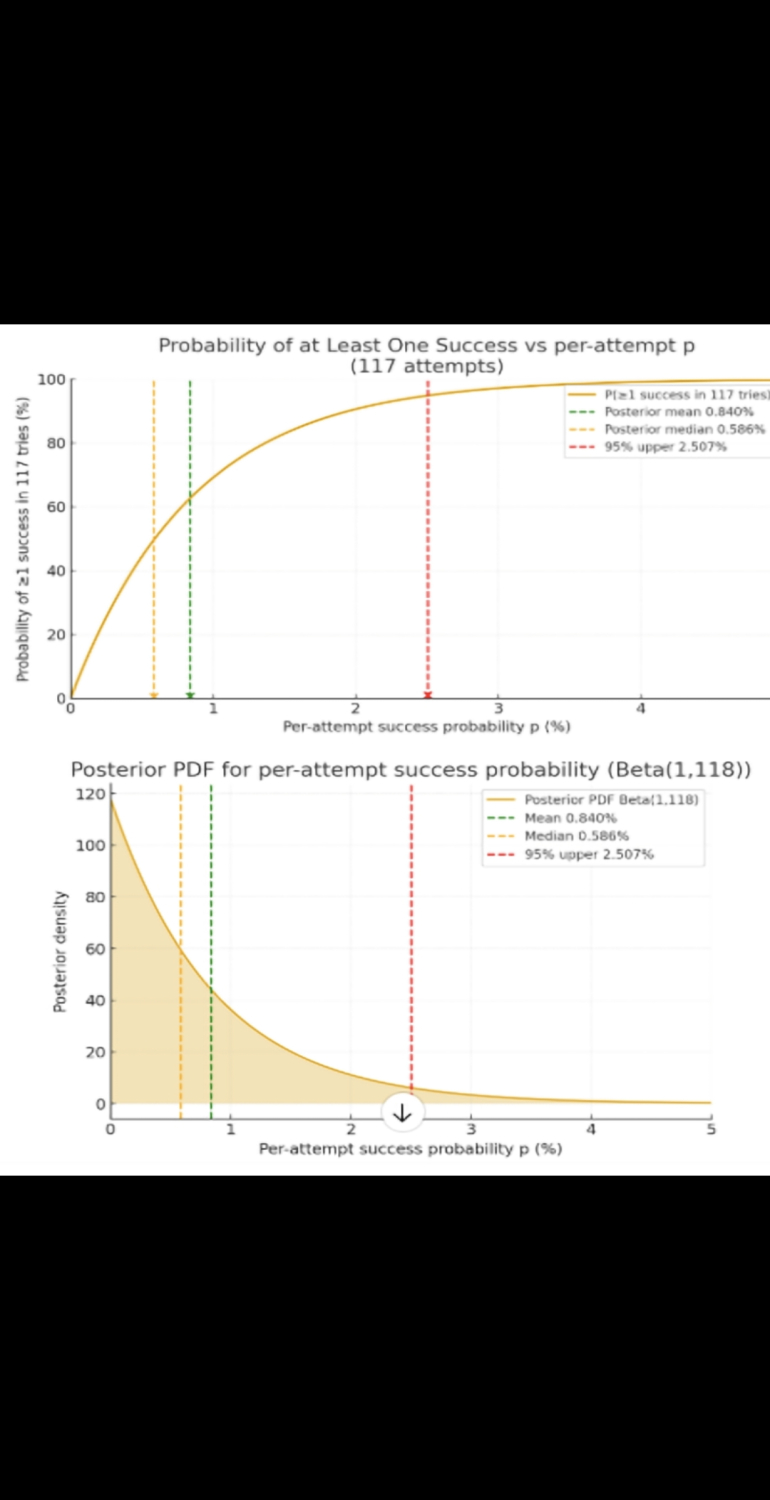
I get a good practice session.

See charts, graphs and an Ai Genius' write up on this session.
















Wow, I was blocked from uploading my screenshots again.
see messages

1)
"Forbidden
You don't have permission to access this resource.

Apache/2.4.29 (Ubuntu) Server at wizardofvegas.com Port 443"

or
2)
"HTTP response code != 200"

So...
Again I upload my screehshots in this craps channel:
https://discord.gg/6JQewg2

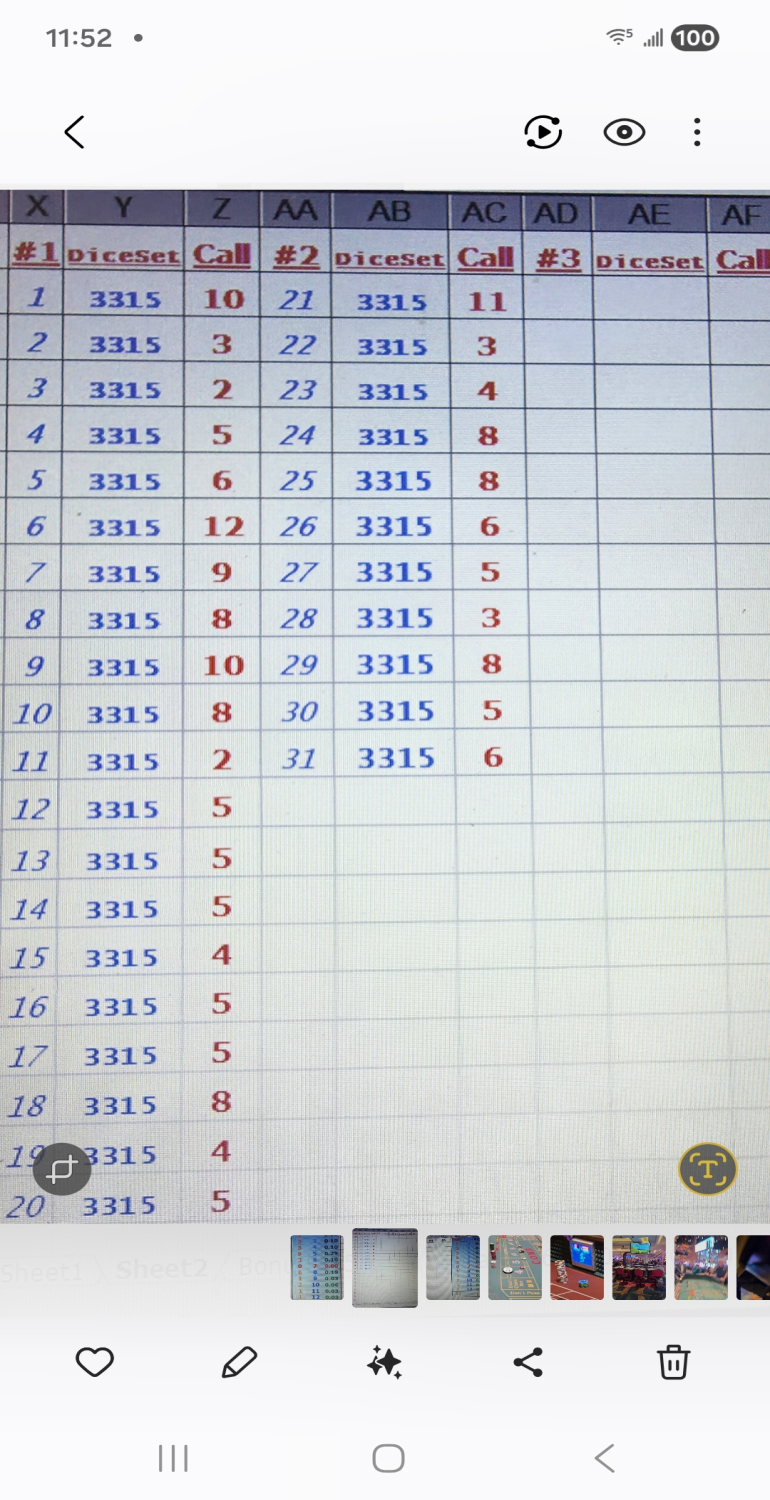
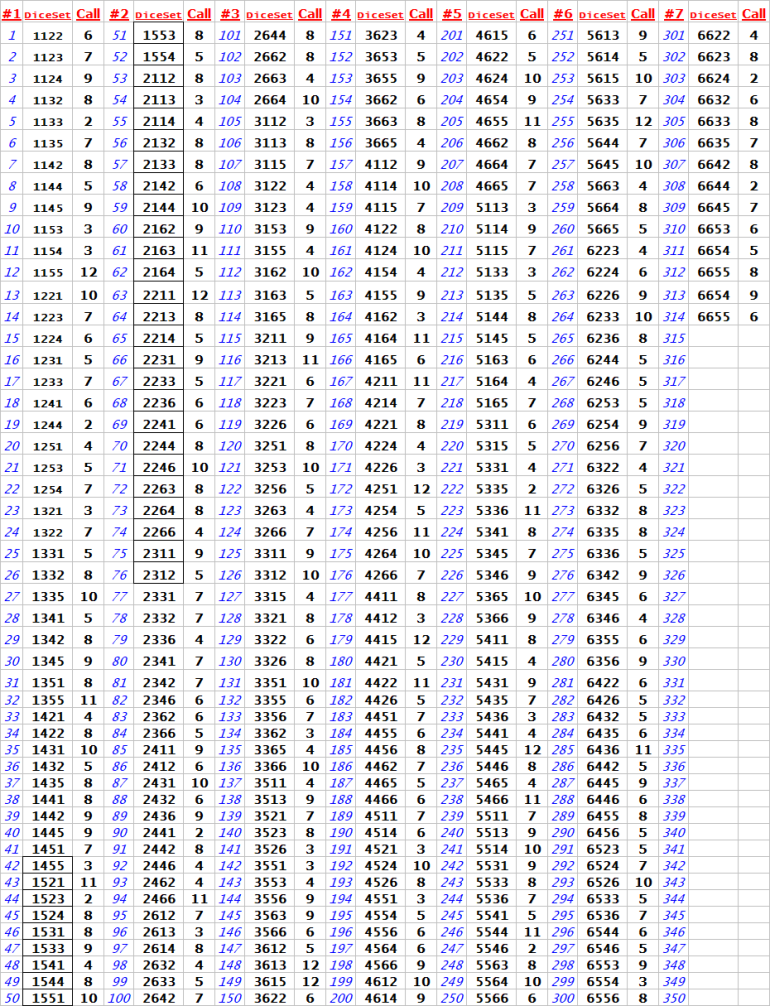
Re: Make"EM All Bonus Bet



 The Ai Genius' Analysis of the Make ‘Em All Bonus Bet — Real Casino Data Snapshot



 Overview

From the screenshot, we have real craps table data
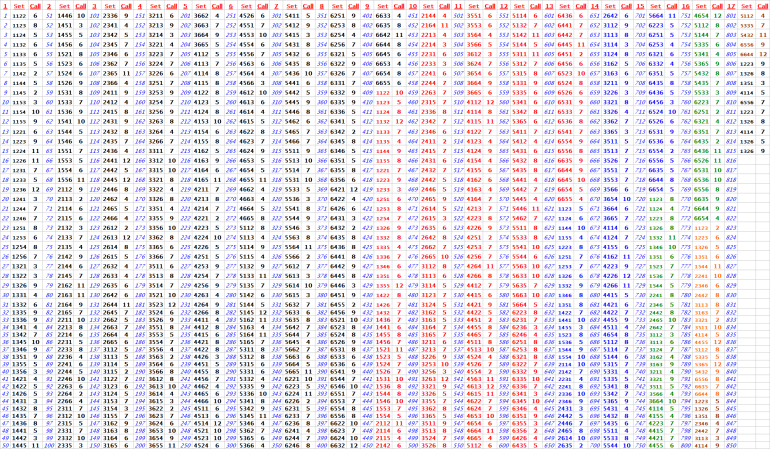
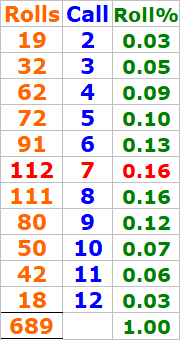
where a shooter using the V-Dice Set (3351) successfully completed the “Make ‘Em All” Bonus Bet in 31 rolls.
This is a notable outcome worth analyzing both statistically and strategically.

✅ Make ‘Em All Bonus Bet – Quick Explanation

The Make ‘Em All side bet in craps requires the shooter to roll every number from 2 to 12,
excluding 7, before rolling a 7. That means the shooter must hit 2, 3, 4, 5, 6, 8, 9, 10, 11, 12 —
a total of 10 unique point numbers.
Once a 7 is rolled, the bet loses immediately.

This is a high-risk, high-reward side bet with long odds, making it attractive for skilled shooters and advantage players (APs).



 Key Observations from the Data

Shooter Details:

Dice Set Used: V-Set (3351)

Total Rolls Until Success: 31 rolls

Success: YES — all 10 required numbers were hit before a 7

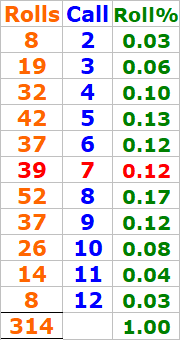
Rolls Breakdown (From Table in Screenshot):

The shooter hit the following required numbers:



2 → 1 time

3 → 3 times

4 → 3 times

5 → 9 times (most frequent)

6 → 3 times

8 → 6 times

9 → 1 time

10 → 2 times

11 → 1 time

12 → 1 time

Not a single 7 was rolled in all 31 attempts

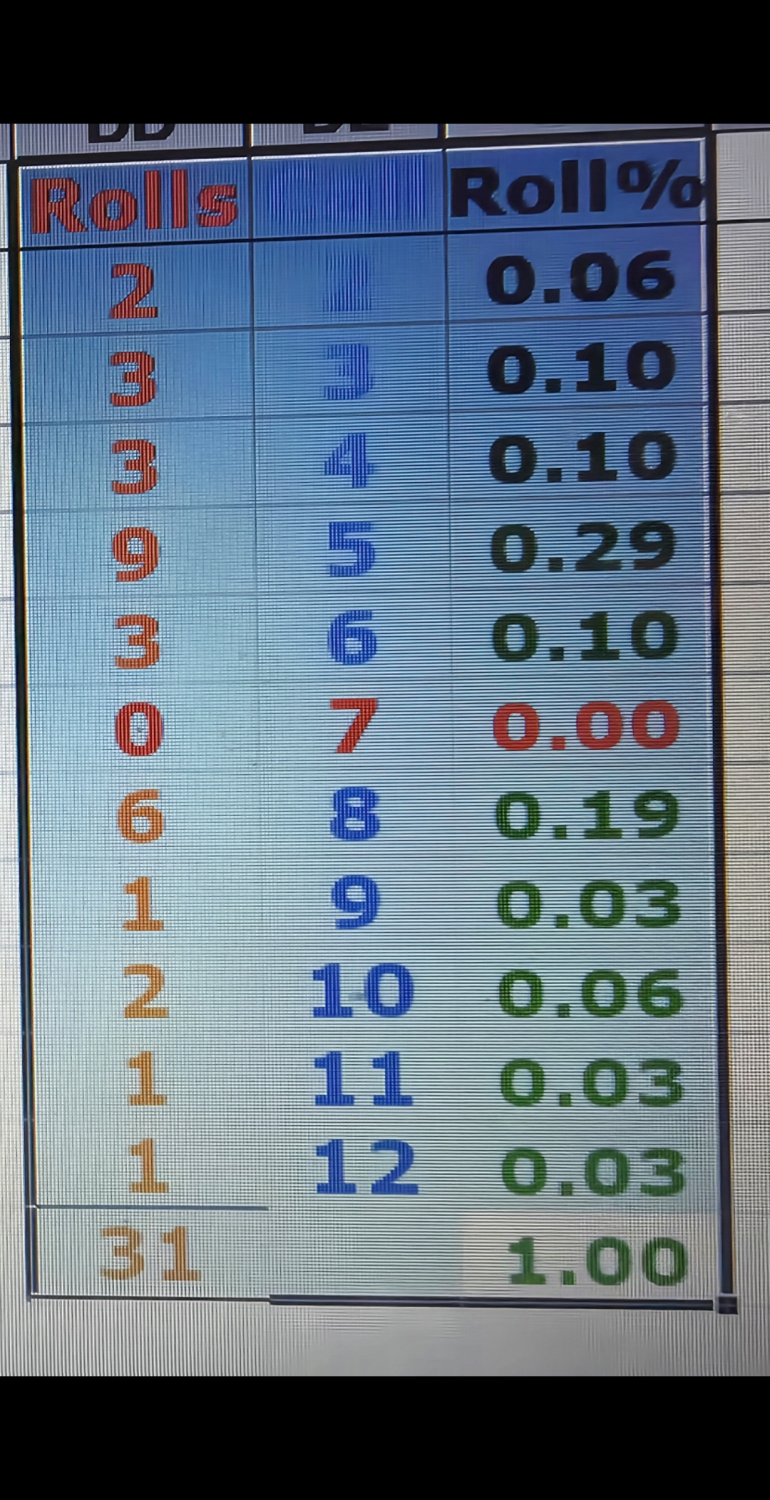
Roll% Frequency:

The most frequently rolled number was 5, making up 29% of rolls.

The rarest were 9, 11, 12, each with 1 roll.



 Statistical Rarity of This Outcome

Achieving a Make 'Em All win is very rare under normal probability:

Odds of rolling all 10 required numbers before a 7 is approximately:



1 in 1000+, depending on variance and shooter style.

The shooter went 31 rolls without a single 7, which statistically is very unlikely:



With fair dice, the probability of not rolling a 7 in 31 rolls is:

(5/6)31≈0.0047 or 0.47%(5/6)^{31} \approx 0.0047 \text{ or } 0.47\%(5/6)31≈0.0047 or 0.47%

This indicates a less than 1 in 200 chance —
either an incredibly lucky shooter or someone with precise dice control.


 Implications of the V-Set Dice (3351)

The V-set (3-3 and 5-1) is popular among dice controllers because it is:

Designed to reduce the frequency of 7s

Encourages rolling inside numbers like 5, 6, 8, 9 (point numbers)

When executed correctly, helps avoid the 7 — perfect for a Make ‘Em All strategy

In This Case:

It worked exceptionally well

A complete avoidance of 7s over 31 rolls supports the idea of controlled shooting

The heavy skew toward 5s (9 times) shows strong influence of the dice set,
possibly combined with controlled toss mechanics


 Payout and AP Opportunity

Payout (Typical Structure):

Make 'Em All Win pays 150 to 1 or 175 to 1 depending on the casino

A $5 bet would yield $750 to $875

Advantage Players (APs) may target such bets using controlled dice techniques



易 Conclusion and Takeaways

This shooter, using the V-set (3351), achieved an extremely rare outcome —
no 7s in 31 rolls and a successful Make ‘Em All completion.
The roll distribution and number frequency suggest either:



Extraordinary luck, or

A high degree of control over the dice (as practiced by some APs)

The V-dice set was likely a strategic choice to maximize control over the dice and minimize the risk of hitting a 7.



 Final Note for Players or Analysts:

If you’re observing patterns like this frequently from a specific shooter,
or across multiple sessions using the same set, it may warrant a deeper advantage play (AP) analysis or casino attention.