Thread Rating:
Is there anything special about a shooter rolling the dice at least 9 rolls (assuming he reaches the Captain's 5-Count with the first number being a box number) indicating that he is more likely than not to experience a long roll? On the 9th roll shooter does not have to show a box number.
In the first instance, 2.8 explains why many old-timers say, "take one or two hits, then down". A heck of a lot safer although the poll here shows the PSO is likely to come right after a point has been established.
Thank you for any comments.
For example, if a shooter throws 8, 5, 10, 8 (made point), 2 (craps), 6, 11, 2, 7 (seven out), that is "9 rolls before a PSO" using the method that results in 8.6.
How Long is a Craps Roll?Quote: eclecticOne number is 2.8 (or just under 3) and the other is 8.6 (or just under 9).
Don Catlin (rest his soul) shows how and why these are computed
http://catlin.casinocitytimes.com/article/how-long-is-a-craps-roll-1240
the number of rolls per pass line decision = 557/165 or
3.3757575757575757575757575757576
the number of pass line decision or games (rounds) = 495/196
or 2.5255102040816326530612244897959
that makes the average number of rolls in a craps hand (includes the 7 out) = 1671/196
(557/165 * 495/196)
or about
8.5255102040816326530612244897959
(8.53)
<<<>>>
for the length of a shooters hand distribution
(like roll 3 and 2 fight for the top roll to 7 out on)
Mr. Catlin looks to be one of the 1st (if not THE 1st at the end of 1999)
to calculate that using a transition matrix
http://catlin.casinocitytimes.com/article/how-long-is-a-roll-part-2-1232
just a simple recursion in Excel does just fine too (finer)
in Google
https://goo.gl/jXMmsV
Certainly makes sense t me about 1/2 hits and down on place bets.
Interestingly, the transition matrix seems to support evidence for use of the Captain's 5-Count. In fact I now remember the reference to Mr Catlin in one of Scoblete's books.
But what about the hypothesis that IF a shooter reaches 9 rolls, that roll will likely continue more often than not? I must get Zumma but probably wouldn't know
how to properly use it.
PSO = point seven out. E.g. you establish a point and seven out on the next roll.
So the number of rolls until you PSO is always 2, lol.
What the OP is actually asking is the average (mean) number of rolls of the average craps hand. I.e. number of rolls before you seven out, or SO (without the P). PSO is always 2 rolls.
no. there is another thread where I not only verified the mathQuote: eclecticInterestingly, the transition matrix seems to support evidence for use of the Captain's 5-Count.
results of the 5 count by SN Ethier
I showed by just waiting 6 rolls then betting
was a much better system than Frank's 5 count.
Beat it hands down! actually slaughtered it, iirc
the thread should still be there if i look for it...
i also remember the Alan M method of '4 rolls and run' was also better than the 5 count
this is on how much money you will lose on average of course it is
https://wizardofvegas.com/forum/gambling/craps/14166-5-count/2/
continue in what way?Quote: eclecticBut what about the hypothesis that IF a shooter reaches 9 rolls, that roll will likely continue more often than not?
one more roll?
2 more rolls?
3 or more rolls??
more likely to go past 20 rolls than one who only has just 3 rolls??
almost an endless list of possibilities.
if a shooter is ready to make that 10th roll we can see what state the hand will be in by looking at me table for a shooters hand.
it shows this
coroll: 0.056325879
4,10: 0.07756502
5,9: 0.089033754
6,8: 0.096466046
there was a 68% chance to NOT make that 10th roll
but given it is to be made (the 10th roll)
about a 17% chance the 10th roll is a come out roll and the shooter can not 7 out on that roll
that makes about 83% chance a point is established
and the 7 out could be the next roll...
just a matter of when
unless the shooter says "I am done and gone after a pass line win" and the casino needs to find another shooter to get the 7 out and finish the current hand if there are any contract bets left waiting to be resolved.
This may happen late at night when the players are tired and almost done, i wood guess.
Sally, thank you for providing the correct statistics on the 5-count, and especially for posting the math on the most effective way of avoiding the PSO with the
'4 and run' and '6-count' methods.
I missed out on these posts by not following up on reading the thread.
Further to this discussion, I will be posting some data from 7,500 craps rolls by researching what I have labeled the '9-Count Method'.
For those who have tested a system with the Zumma data, perhaps this can serve as an out-of-sample test. I'll post the individual stats tomorrow but for
now here is the concept.
9-Count Method
Rule 1: Shooter reaches "The Captain's' 5-Count.
Rule 2: Player begins betting AFTER the 9th Roll.
Total number of Events: 75
(Number of times Shooter reached the 9-Count from 7,500 craps rolls)
PSO On Roll Number Number of Events
PSO on Roll #10 6
To be continued........
PSO on Roll # 10.........6 occasions
PSO on Roll # 11.........6 occasions
PSO on Roll #12...........7 occasions
Continued on next post.....
PSO on Roll #13..........6 decisions
PSO on Roll #14..........6 decisions
PSO on Roll #15...........3 decisions
PSO on Roll #16..........7 decisions
PSO on Roll #17..........3 decisions
PSO on Roll #18...........5 decisions
PSO on Roll #19...........3 decisions
PSO on Roll #20...........2 decisions
PSO on Roll #21...........1 decisions
PSO on Roll #22...........3 decisions
PSO on Roll #23...........3 decisions
PSO on Roll #24...........3 decisions
PSO on Roll #25...........1 decisions
PSO on Roll #26...........2 decisions
PSO on Roll #27 - 31 Zero decisions
PSO on Roll #32...........2 decisions
PSO on Roll #33...........1 decision
PSO on Roll #34 - 37 Zero decisions
PSO on Roll #38 1 decision
Total number of Decisions = 75
OK, let's see how this looks on a post. (Decisions a better word than Occasions)
END
75 should = 71 unless you left out dataQuote: eclecticTotal number of Decisions = 75
why list roll12 2 times?
the percentage of the shooters that went another 6 rolls Max = 48%
looks about right
this can be calculated too by the probability of passing the 5 count and making the 10th roll
lala tea da
<<>>
of course, the 5 count (start/end with a point number)
has no weight at crapless craps where every number except the 7
is a point roll.
the probability that any shooter passes the 5 count there = 0.537663966
regular craps only offers 0.273319616
as the probability in 5 rolls
lots of waiting around and no rating at all while not betting
totally against what Frank S says about his method
waiting for the long rolls that due come
(of course, the number of long rolls and winnings will never make up for the massive amount of short rolls that the 5 count produces. just what it is)
waiting for 5
Hi 5
waiting
"7 out line away
pay all Lay Bets!"
4183 total shooters (8.39 rolls per shooter)
2463 passed the shooter 5-count wait system (0.588811858)
1310 shooters made the 10th roll (1309 also made the 5-count too)
that = 0.313172364
calculated probability = 0.319390699
just doing what the math says
I see nothing impressive in the rest of the data I have
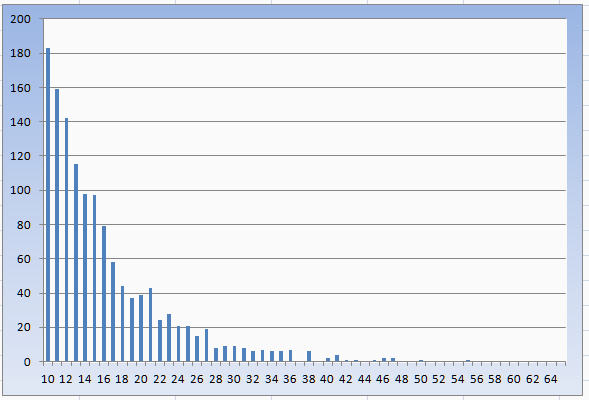
the distribution
| 7out on roll | count | prob | x or less prob |
|---|---|---|---|
| 10 | 183 | 0.139801375 | 0.139801375 |
| 11 | 159 | 0.121466769 | 0.261268144 |
| 12 | 142 | 0.108479756 | 0.369747899 |
| 13 | 115 | 0.087853323 | 0.457601222 |
| 14 | 98 | 0.07486631 | 0.532467532 |
| 15 | 97 | 0.074102368 | 0.606569901 |
| 16 | 79 | 0.060351413 | 0.666921314 |
| 17 | 58 | 0.044308633 | 0.711229947 |
| 18 | 44 | 0.033613445 | 0.744843392 |
| 19 | 37 | 0.028265852 | 0.773109244 |
| 20 | 39 | 0.029793736 | 0.802902979 |
| 21 | 43 | 0.032849503 | 0.835752483 |
| 22 | 24 | 0.018334607 | 0.854087089 |
| 23 | 28 | 0.021390374 | 0.875477464 |
| 24 | 21 | 0.016042781 | 0.891520244 |
| 25 | 21 | 0.016042781 | 0.907563025 |
| 26 | 15 | 0.011459129 | 0.919022154 |
| 27 | 19 | 0.014514897 | 0.933537051 |
| 28 | 8 | 0.006111536 | 0.939648587 |
| 29 | 9 | 0.006875477 | 0.946524064 |
| 30 | 9 | 0.006875477 | 0.953399542 |
| 31 | 8 | 0.006111536 | 0.959511077 |
| 32 | 6 | 0.004583652 | 0.964094729 |
| 33 | 7 | 0.005347594 | 0.969442322 |
| 34 | 6 | 0.004583652 | 0.974025974 |
| 35 | 6 | 0.004583652 | 0.978609626 |
| 36 | 7 | 0.005347594 | 0.983957219 |
| 37 | 0 | 0 | 0.983957219 |
| 38 | 6 | 0.004583652 | 0.988540871 |
| 39 | 0 | 0 | 0.988540871 |
| 40 | 2 | 0.001527884 | 0.990068755 |
| 41 | 4 | 0.003055768 | 0.993124523 |
| 42 | 1 | 0.000763942 | 0.993888464 |
| 43 | 1 | 0.000763942 | 0.994652406 |
| 44 | 0 | 0 | 0.994652406 |
| 45 | 1 | 0.000763942 | 0.995416348 |
| 46 | 2 | 0.001527884 | 0.996944232 |
| 47 | 2 | 0.001527884 | 0.998472116 |
| 48 | 0 | 0 | 0.998472116 |
| 49 | 0 | 0 | 0.998472116 |
| 50 | 1 | 0.000763942 | 0.999236058 |
| 51 | 0 | 0 | 0.999236058 |
| 52 | 0 | 0 | 0.999236058 |
| 53 | 0 | 0 | 0.999236058 |
| 54 | 0 | 0 | 0.999236058 |
| 55 | 1 | 0.000763942 | 1 |
| 56 | 0 | 0 | 1 |
| 57 | 0 | 0 | 1 |
| 58 | 0 | 0 | 1 |
| 59 | 0 | 0 | 1 |
| 60 | 0 | 0 | 1 |
| 61 | 0 | 0 | 1 |
| 62 | 0 | 0 | 1 |
| 63 | 0 | 0 | 1 |
| 64 | 0 | 0 | 1 |
| 65 | 0 | 0 | 1 |
| total | 1309 | x | x |
as expected (pretty and not impressive)
just like winning at craps
nothing impressive
pass with 345x odds and Lay bets
Lifetime winner
so, no one cares
Sally
mental muddle trying to keep track of all the numbers and decisions. Man I hope there are no errors.
I'll await your reply to see if these numbers change any of your conclusions? Also, I many have some follow up questions if you please. Thank you.
PSO on Roll # 10.........6 occasions
PSO on Roll # 11.........6 occasions
PSO on Roll #12...........7 occasions
PSO on Roll #13..........6 decisions
PSO on Roll #14..........6 decisions
PSO on Roll #15...........3 decisions
PSO on Roll #16..........7 decisions
PSO on Roll #17..........3 decisions
PSO on Roll #18...........5 decisions
PSO on Roll #19...........3 decisions
PSO on Roll #20...........3 decisions
PSO on Roll #21...........1 decision
PSO on Roll #22...........2 decisions
PSO on Roll #23...........3 decisions
PSO on Roll #24...........3 decisions
PSO on Roll #25...........2 decisions
PSO on Roll #26...........2 decisions
PSO on Roll #27 - 31 Zero decisions
PSO on Roll #32...........2 decision
PSO on Roll #33 - 35 Zero decisions
PSO on Roll #36........... 2 decisions
PSO on Roll #37 - 41 Zero decisions
PSO on Roll #42.......... 1 decision
PSO on Roll #43............1 decision
PSO on Roll #44 - 47 Zero decisions
PSO on Roll #48............1 decision
Total number of Decisions = 75
END
I'm sure what you say is true, but I would certainly like to hear what Sally has to say about the actual math.
75 looks to adds upQuote: eclecticMan I hope there are no errors.
but I do not have those 7500 dice roll collection to verify.
did you do all 7500 rolls?
I would hope not
7500/8.52 = # of shooters = x
x * 0.32 = number of shooters that passed 5 count and made the 10th roll
that value is about 282
If you did all 7500 rolls
then you must determine the 5-count differently from those that know it starts and ends on a box number
hahaha
the original Frank S. method
your 75 distribution still is very similar to the Zumma one with a sample size of 1,309 shooters
I see no value in long rolls when making large Lay bets
I want my win fast so I can do dinner and dancing
Last week, for example, some LOUD know-it-all shooter (everyone knows the type)
set a point of 4 and I made a $2000 Lay bet (all-in) on the 4 and the shooter did not see it.
Some disturbance about the hardways being on or off... they paid him I think
He went out on the 7 on his 22nd or 23rd roll (I lost count) and I screamed
Yahoo!! real LOUD. No Craps!
He rolled so many crap numbers (crap) all lost in that hand, except me
happens a lot
must be my pretty face!
Shooter must reach Frank S. original method for calculating the 5-Count. (Count begins and ends on a Box Number.)
Shooter must then roll the die 4 additional rolls to equal a total of 9 rolls. This of course includes the Come Out.
Than the study began. 5-Count reached: rolled the dice 4 additional times for a total of 9 rolls.
I'm repeating myself here but want to clarify that the 9-Count did NOT have to end on a Box Number.
Would you like me to go through the data again, using the Frank S. method of the 9-Count ENDING on a Box Number?
Any additional value to be gleaned from the data using that process?
Appreciate your input.
Any value in the data at all? Ever? Using any process?Quote: eclecticAny additional value to be gleaned from the data using that process?
Appreciate your input.
Unless you have a time machine and can go back, identify those rolls and bet on them.
How many times and how many ways must the gambler's fallacy be defined? 7500?
Ah, okQuote: eclecticI'm repeating myself here but want to clarify that the 9-Count did NOT have to end on a Box Number.
so basically you want to see FrankS's 5-count-Plus1Any
5-count-Plus2Any
5-count-Plus3Any
5-count-Plus4Any and so on
that has this form
1Box-3Any-1Box-XAny
X=1,2,3 or 4 or higher than 4
it will not change the distributions one bit from just the 5-count and 0any
or
making that 10th roll
some may think it will
ok
<<<>>>
Frank's method does not do what he claims on the 35,097 actual Zumma dice rolls
ands
he has never produced actual dice rolls and his method
to gain the edge over the house from higher comps (haha)
less bets and finding those mystery rollers that be the true God's gift to all humans
<<<<>>>>
picture Frank and 15 other Frank DIs at the same table all using the 5-count
Frank is first to roll
only he bets $5 pass line. All others are waiting even on him.
7 winner!
next roll 7 winner!!
Frank IS HOT!!
other players are waiting around the table to play seeing Frank yell and scream!
Frank rolls a 6 for his point.
1-count
no other bets yet from the 15 other players
and this will be allowed by the box person!
hahaha
funny stuff
some have much fun coming up with fun ideas
that is fun
thanks for sharing yours!
Here's the long answer and the short answer: each roll is totally, utterly, inescapably independent. If you want to make a place bet, make the bet. If you want to take it down, take it down. You have no better or worse chance of winning any given bet based on how many times you've won it since the last seven-out.Quote: eclecticDeMango, probably easy for you to say because you have lots of experience at craps? Some newbies, like myself, appreciate how players here with superior math skills evaluate the game to form a method of play.
If you take your bets down and wait for a shooter to seven-out, the effect is simply that you're betting less over time. That means you win less and lose less. It absolutely does not increase your chance of winning any of the bets you make. A place 6 bet made immediately after the shooter gets the dice and establishes a point of 10 is exactly as likely to win as a place 6 bet that's been up for 80 rolls and the shooter is working on his 14th point. Past events have no bearing on whether your next place 6 bet wins.
not soQuote: MathExtremistA place 6 bet made immediately after the shooter gets the dice and establishes a point of 10 is exactly as likely to win
as a place 6 bet that's been up for 80 rolls and the shooter is working on his 14th point.
Past events have no bearing on whether your next place 6 bet wins.
from Frank Scoblete (born 1947)
who claims to be a craps expert (and allows others to call him a craps expert)
http://www.goldentouchcraps.com/proof.shtml
"C. shooters who had developed a "rhythmic roll" that was an unconscious controlled dice shot; this through trial and error in the casinos
D. shooters who were conscious rhythmic rollers or, as we now call them, dice controllers who had purposely learned how to flip the game into the positive zone when they rolled the dice"
Frank also says some shooters are better at getting on HOT rolls than others
that is what the 5-count (1+3+1) is mostly all abouts
one expert against another expert
never ends
thank you!
I understand the theory behind the 5-count is that some players may have longer rolls, and since longer rolls are "good," putting more of your money on the longer rollers is beneficial. It sounds superficially like card counting, but the problem is that "long roll" doesn't actually correlate with "more winning" for a given bet. If a shooter has a longer average roll because they roll lots of 3s and 12s, the come bettor will get killed. If the shooter has a longer average roll because they roll more 4s and 10s but fewer 6s and 8s, the inside place bettor will get killed. In cases like those, the 5-count bettor may lose money depending on how they bet. In other words, contrary to popular wisdom, "long" rolls are not necessarily better rolls. It depends on which bets you're making. That's why any single statistic that measures the length of a roll, or worse, a crude proxy like SRR, is insufficient for an intelligent gambler to understand whether they have an advantage. It takes more information. For example, knowing the edge on the place 6 bet requires knowing the expected ratio of 6s to 7s, not the expected length of a hand or how often a 7 rolls.
But statistics like hand length or SRR are easy to compute. That's why they're so easy to sell to gullible gamblers looking for an edge.
Sorry it could not have been more productive, unless one can learn from the info posted about the law of large numbers, independent trials, and gamblers fantasy.
Take it at face value or learn it the hard way? As the quote goes, "Entrenched belief is never altered by the facts."
of course not, because now you have it.Quote: eclecticI don't regret spending the time gathering the data.
I show the Zumma Craps System Tester as having 2,086 shooters passing the 5-count (0.498685154)
this is a corrected value (now I have that too)
1,140 passing the 5count-4moreCount (0.272531676)
(a quick change to my wincraps code and done - less than 60 seconds)
the probability of any shooter making the 11th roll = 0.275546562
(that comes from the 5.8 average number of rolls to pass the 5-count + 4 more rolls)
the distribution in view (no data table)
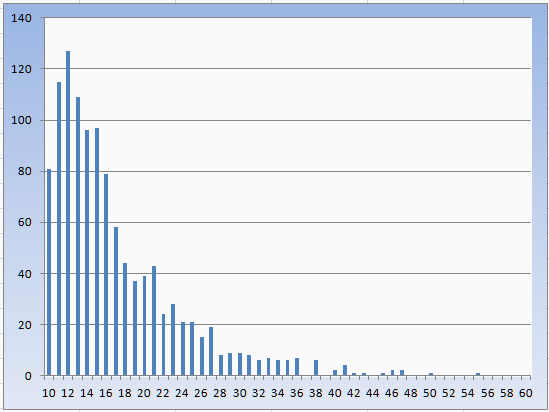
the 7 out happening by the 15th = abouts 0.548245614
by the 16th = abouts 0.61754386
Sally
Quote: DeMangoWhy has not anyone been Captain Obvious here? PSO means Point Seven Out. Two rolls, that's it, no coffee. Want to make money? Practice tossing the dice for seven years. Work on a shot that produces 18 yo's in a row.
I did point it out, back on page one.
Quote: IbeatyouracesThe five count is nothing but Gamblers Fallacy.
Heh.
Quote: mustangsallyI showed by just waiting 6 rolls then betting
was a much better system than Frank's 5 count.
Beat it hands down! actually slaughtered it, iirc
LOL. I was going to say, I know a great system too! Wait for 23 rolls before betting. You don't get a lot of action down on the table, but you also cut your losses significantly!
Quote: MathExtremistIf you take your bets down and wait for a shooter to seven-out, the effect is simply that you're betting less over time. That means you win less and lose less.
I would have just said "lose less." :) But I assume your meaning is that when you bet less, you are less likely to have a big winning session, which is of course true.
-----
PROBABILITY TO GET AN UNKNOWN POINT X=(40/99)^n
1st Point: 40.404% (40/99)
2nd Point: 16.320% (40/99)^2
3rd Point: 6.596% (40/99)^3
4th Point: 2.660% (40/99)^4
5th Point: 1.077% (40/99)^5
6th Point: 0.435% (40/99)^6
7th Point: 0.176% (40/99)^7
8th Point: 0.070% (40/99)^8
-----
Next, what is the HE on Small/Tall and All?
Thank you
where did you find that?Quote: rushdlPROBABILITY TO GET AN UNKNOWN POINT X=(40/99)^n
It should be like this
(3/24*1/3 + 4/24*4/10 + 5/24*5/11) * 2
wolfram alpha
(set point of 4 and win + set point of 5 and win + set point of 6 and win) * 2 for 10,9 and 8 points
<<<>>>
67/165 (201/495) = p
and your table is for at least X points
at least 1 Point: a% (p)
at least 2 Points: b% (p)^2
now this about probability and HE
what are you after, exactly?
Quote: mustangsallywhere did you find that?
https://wizardofvegas.com/forum/gambling/craps/24931-odds-of-obtaining-the-point/
Whats wrong with it?
it does not agree with thisQuote: rushdlWhats wrong with it?
"Given that a point is established,
the probability that the shooter makes the point is pr(point is 4 or 10) ×pr(making 4 or 10) + pr(point is 5 or 9) × pr(making 5 or 9) + pr(point is 6 or 8) ×pr(making 6 or 8) =
(6/24) × (3/9) + (8/24) × (4/10) + (10/24) × (5/11) = 201/495 = 0.406061."
https://wizardofodds.com/ask-the-wizard/craps/probability/
looks to me
the same person has given 2 different answers.
must be a simple reason for that, i wood guess
Quote: mustangsallylooks to me
the same person has given 2 different answers.
must be a simple reason for that, i wood guess
Doesn't 40/99 = 201/495 to not many decimal places? $:o)
It's really 40.20/99 but the 0.20 was kept by the house as commission.Quote: OnceDearDoesn't 40/99 = 201/495 to not many decimal places? $:o)
Origins of 3-4-5X Odds
Reliable sources (a boxman and floorman at Bally's) tell us that 3-4-5X odds wasthe idea of a high-rolling player named Stanley L., sometime around the early 90's.(We believe we know his last name but decline to reveal it for the sake of privacy.)Because he was a high roller, one side of a table that was reserved solely for hisplay. As Stanley was strictly a Pass Line and Come player, he convinced the crapspit at Bally's to allow him to use the 3-4-5X odds as it was easier for him to understandthe pay offs on wins, since every win meant the same payout -- seven times the flatbet on wins where full free odds were taken. What we don't know is what the originaltable odds were. That is, did the casino raise the odds from 2X upward orreduce from 5X downward?
What ever happened to Stanley L.? It was stated that he ran up over a million dollarsin markers and was never seen again.
Quote: mustangsallyit does not agree with this
"Given that a point is established,
the probability that the shooter makes the point is pr(point is 4 or 10) ×pr(making 4 or 10) + pr(point is 5 or 9) × pr(making 5 or 9) + pr(point is 6 or 8) ×pr(making 6 or 8) =
(6/24) × (3/9) + (8/24) × (4/10) + (10/24) × (5/11) = 201/495 = 0.406061."
https://wizardofodds.com/ask-the-wizard/craps/probability/
looks to me
the same person has given 2 different answers.
must be a simple reason for that, i wood guess
Usually these things are because of the nuance of the question.
I believe the difference would be I asked for odds before the come-out with no point established, a bit different yes?
Quote: blackjackSwitchNERDDDDD
Personal insult.
Any significance to prime numbers as they relate to casino craps? I noticed the first few are either craps or 7.
https://www.mathsisfun.com/prime_numbers.html
OK, so it may be a stupid question?
http://quoteinvestigator.com/2010/05/17/remain-silent/
Thank you.
I preface this by understanding the following question would break one of the Wizard's commandments: don't hedge.
I can see (at least for now) the concept of hedging if making big dollar bets as good play to decrease variance or volatility?
If betting the DP w/the Iron Cross as a hedge (2units on the 5,6, or 8 and one unit on the field) is there an ideal ratio of
how much money should be placed on the DP vs the Iron Cross? Thank you.


