Thread Rating:
To over clarify this, a roll of 3,7,3,7 would constitute 4 decisions already before a point is even established. Again, in 10 decisions how often would you NOT see two DP winners in a row?
Thanks
i think this has been asked a few time B4
betting systems asked
1st for the pass line then for the dpassQuote: AtGame7How often or how likely will it be to go 10 pass line decisions and NOT hit two don't pass wins in a row?
This includes everything associated with a pass line decision, come out rolls (repeated ones if that's the case) and points made/missed.
Thanks
well, i think for the pass line NOT seeing 2 in a row is easy
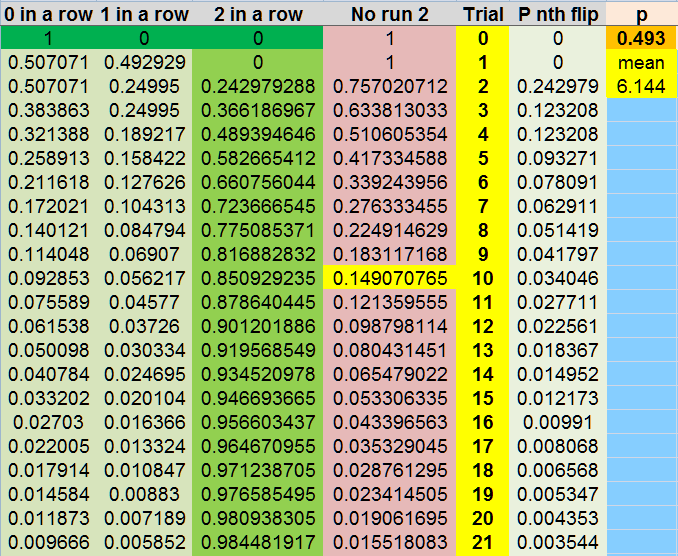
as there are only 2 possible outcomes, win/lose making 2^10
1,024 possible sequences
that probability = abouts 0.149070765 or 1 in 6.71
this is 1 - the prob of at least 1 such run in 10 decisions
2nd
for the dpass one can now win/lose/push
3 possible outcomes for each pass line decision
3^10 = 59,049 possible sequences
they could be listed and counted
but you have to decide if this is what you really want
for dpass example
WLLLW PWLWL <<<do you count this as 2 in a row Wins even with the push at decision 6
Dec#6 was a Loss for the pass line
i say, without any more looking, the results for pass line should be close enough for the dpass
unless you require exact probabilities...
but i still may list and count for the fun of it
or just a simple Markov chain in Excel should do
added
here it is

i get
no run
0.158729947
1 in 6.30
1% off the pass line
so, in other words
a PUSH does NOT break a W streak
WLLLW PWLLW is counted as 2 Wins in a row
if you want to know how to do this using a spreadsheet
you have to wait until i am feeling better
Sally
I was not close in my guess which I am embarrassed to tell you was nearly twice the correct answer.
you are welcomeQuote: AtGame7MORE then close enough without further work required. Thank you!
I was not close in my guess which I am embarrassed to tell you was nearly twice the correct answer.
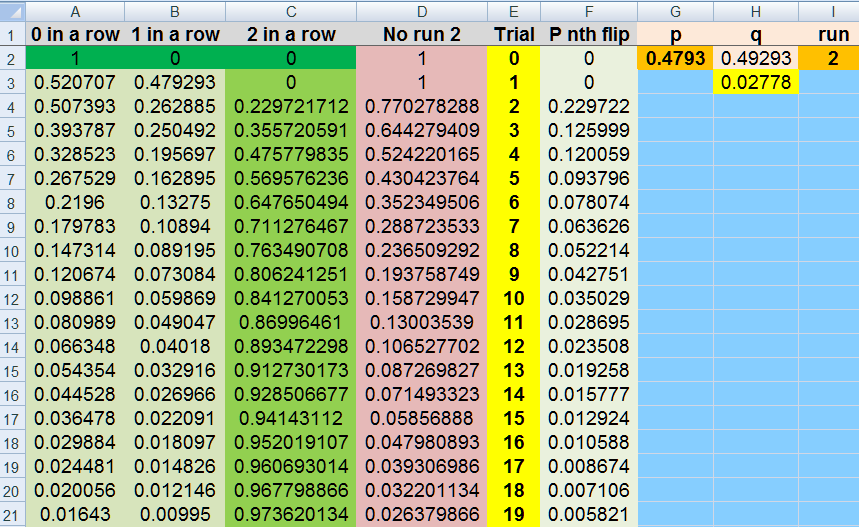
it was a simple solution
I added it
and here again
simple recursive in Excel
for me even fighting a cold and flu and yuk
thank you for sharing what you thought!
Sally
added as my ears plug up
with a fair coin flip 50/50
the chance of NOT getting two heads in a row in 10 flips = 144/1024
0.140625
1 in 7.11
1024 = 2^10
and 144 = the 12th Fibonacci number (where to get the next # we add the previous 2)
1
1
2
3
5
8
13
21
34
55
89
144
ok
In a run of 10 pass line decisions where no two consecutive are DP wins, there are:
1 way to have all 10 lose
10 ways to have 1 win (decisions 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10)
36 ways to have 2 wins:
1,3-10 (i.e. 1 and 3, 1 and 4, 1 and 5,..., 1 and 10 - not 1 and 2, as those are consecutive)
2,4-10
3,5-10
4,6-10
5,7-10
6,8-10
7,9-10
8,10
56 ways to have 3 wins:
1,3,5-10
1,4,6-10
1,5,7-10
1,6,8-10
1,7,9-10
1,8,10
2,4,6-10
2,5,7-10
2,6,8-10
2,7,9-10
2,8,10
3,5,7-10
3,6,8-10
3,7,9-10
3,8,10
4,6,8-10
4,7,9-10
4,8,10
5,7,9-10
5,8,10
6,8,10
35 ways to have 4 wins:
1,3,5,7-10
1,3,6,8-10
1,3,7,9-10
1,3,8,10
1,4,6,8-10
1,4,7,9-10
1,4,8,10
1,5,7,9-10
1,5,8,10
1,6,8,10
2,4,6,8-10
2,4,7,9-10
2,4,8,10
2,5,7,9-10
2,5,8,10
2,6,8,10
3,5,7,9-10
3,5,8,10
3,6,8,10
4,6,8,10
6 ways to have 5 wins:
1,3,5,7,9
1,3,5,7,10
1,3,5,8,10
1,3,6,8,10
1,4,6,8,10
2,4,6,8,10
It is impossible to have 6 or wins out of 10 without at least two being consecutive
The total probability is:
(1 x (1-p)10) + (6 x p x (1-p)9) + (36 x p2 x (1-p)8) + (56 x p3 x (1-p)7) + (35 x p4 x (1-p)6) + (6 x p5 x (1-p)5)
where p is the probability of a Don't Pass win
I calculate p to be the sum of:
1/12 (the probability of rolling a 2 or 3 on the comeout)
2 x 1/12 (the probability of rolling a 4 or 10 on the comeout) x 2/3 (the probability of sevening out)
2 x 1/9 (the probability of rolling a 5 or 9 on the comeout) x 3/5 (the probability of sevening out)
2 x 5/36 (the probability of rolling a 6 or 8 on the comeout) x 6/11 (the probability of sevening out)
= 949 / 1980
and the solution = 0.1662674
me tooQuote: ThatDonGuyI get 16.63%, both through simulation and through brute force math
except i used simple math in Excel
that result means a PUSH breaks the Win streak

I went the other route (push does not break a Win streak)
as this sounds like a betting system idea
and we may never know
Sally
I chose 10 decisions because that is the point the bets starting getting way too large to justify only winning one tor two units should you complete the parlay. If you are curious at all, on a $5 table it would look like this:
$5 bet follow by a $10 bet should the first bet lose. If the $10 bet loses you stay at $10 but must parlay the winnings to $20, if the third bet in the progression loses you can stay at $10 parlay the winnings (that parlay wins you $5 total). Your bets then increase to 15/20/25/30/35/40 with each one being parlayed should it win. At any point you win a parlay you have won a $5 unit.
A runout of 10 decisions without either winning one of the first two bets or going 10 without two wins in a row cost you $175. Great way to increase your time at the table, if that is what you are into.
Disclaimer, I may not have the above perfect, but I think it's right.
sounds familiarQuote: AtGame7Thank you again, it is indeed a betting system posted on another forum. <snip>
i think your system total loss = 190
05
10
10
15
20
25
30
35
40
----
190
you also said this
"At any point you win a parlay you have won a $5 unit"
no so
must start all over
$25 total bankroll example
here is why
$5 loss
$10 loss
total loss = $15
only have $10 left
win $10 now new bet = $20 (is this the path to take?)
win $20 = $40 and down
$25 = start bankroll
this parlay won $15 net, not $5
if my 4th bet was again $10 and NOT a $20 parlay
i now have $10 +$20 = $30 - $25 bankroll = $5 profit
is thhis the path to take?
sounds like a long and winding road to me
++
(99.7784% = a regular 9 step Marty one-time win prob as a comparison. of course this requires a 511 unit bankroll)
this awful system (negative progression) in me opinion and help from Excel
edit: i will see how awful this system really is
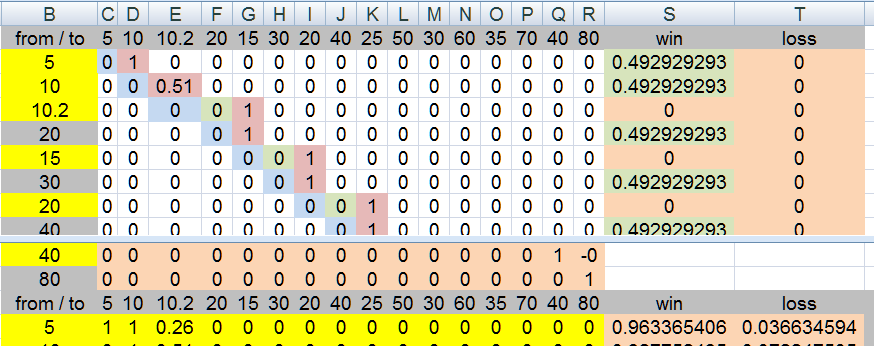
with the pass line
I show a $5 system win = 0.963365406
dpass = 0.963393015
EDIT: Fri 13th
so with an average win of better than $5 per parlay win
must re-calculate the possible winning paths
my matrix is still correct for win/lose prob, maybe, as i currently understand the betting progression
but it needs to multiply a payout matrix to get the avg win at each step
that comes later
Sally
Quote: mustangsally
I went the other route (push does not break a Win streak) as this sounds like a betting system idea
In that case, there are 17,711 different sets of win/loss/push results, and I also get 0.15873.
In fact, there's a non-recursive formula for this:
P(n) = ((A + 1) xn - (B + 1) yn) / (A - B)
where:
W = the probability of winning
L = the probability of losing
x = (2 - 2W - L) + sqrt(L2 + 4WL)
y = (2 - 2W - L) - sqrt(L2 + 4WL)
A = 2L / (sqrt(L2 + 4WL) - L)
B = -2L / (sqrt(L2 + 4WL) + L)
that is niceQuote: ThatDonGuyIn that case, there are 17,711 different sets of win/loss/push results, and I also get 0.15873.
i hope you had fun doing that
math is fun
but as i show in me last post (i do not remember it as this flu is nasty),
does not at all help out the OP for his system, again in my opinion
"for this" = what?Quote: ThatDonGuyIn fact, there's a non-recursive formula for this:
P(n) = ((A + 1) xn - (B + 1) yn) / (A - B)
where:
W = the probability of winning
L = the probability of losing
x = (2 - 2W - L) + sqrt(L2 + 4WL)
y = (2 - 2W - L) - sqrt(L2 + 4WL)
A = 2L / (sqrt(L2 + 4WL) - L)
B = -2L / (sqrt(L2 + 4WL) + L)
in other words
"What'chu talkin' 'bout, Willis?
Mully
Quote: mustangsally
Quote: ThatDonGuyIn fact, there's a non-recursive formula for this:
"for this" = what?
The probability of n consecutive bets not having two consecutive wins (or a win followed by one or more pushes followed by another win)
In this case:
W = the probability of a Don't Pass bet winning = 1/36 + 2/36 + (6/36 x 2/3) + (8/36 x 3/5) + (10/36 x 6/11)
L = the probability of a Don't Pass bet losing = 1 - 1/36 - W
(the 1/36 is for a 12 (or 2, if you're in Reno/Tahoe) on the come out roll, which is a push)
Detailed proof available on request, but it requires that you know what eigenvalues and eigenvectors are.
ah, okQuote: ThatDonGuyThe probability of n consecutive bets not having two consecutive wins (or a win followed by one or more pushes followed by another win)
<snip>
Detailed proof available on request, but it requires that you know what eigenvalues and eigenvectors are.
yes,
i do know about eigens and how to use them
but for this (The probability of n consecutive bets not having two consecutive wins)
i stay on a well traveled path
if you do find gold an easier way
share
matrix multiplication too
is rather simple simple stuff
so, what you think about OP betting system?
or not think?
me too
Sally
Quote: mustangsallyso, what you think about OP betting system?
The same as you - in addition to the Gambler's Fallacy, the progression doesn't always guarantee a $5 win after each parlay.
To have a sequence where two consecutive winning bets results in an overall run of +5, each bet after the third is 1.5 times the previous bet, which is hard to do when you need to bet 75.9375 on the eighth bet of a run and the casino is out of $0.9375 chips at the moment.
Remember - the probability of a bet losing after five losses in a row is the same as the probability of that same bet losing after five wins in a row. A result is no more "due" the sixth time than it was any of the five previous times.


