Chances of winning with a $200 bankroll

Last April I won over $2000 starting with $200 by playing the Don't with full odds (345) and playing 1 or 2 Don't Come with full odds. I am going back to Vegas this April and I wanted to try the same strategy and was wondering what my chances are.

Starting with $200 on a $10 table and playing the Don't Pass with full 345 odds and playing one Don't Come also with full odds, what are my chances that:

I will lose $200 without ever being up.
I will win $100.
I will win $200.
I will win $1000.
I will win $2000.
I will win $10,000.

Thanks!

P.S.: Mustang Sally was a great help last year with all of his calculations. I hope he is still here!

I can't help with the math, however I can help with MSally. My first pointer is I wouldn't call her a he. :)

Quote: longtimelancer

Last April I won over $2000 starting with $200 by playing the Don't with full odds (345) and playing 1 or 2 Don't Come with full odds. I am going back to Vegas this April and I wanted to try the same strategy and was wondering what my chances are.

Starting with $200 on a $10 table and playing the Don't Pass with full 345 odds and playing one Don't Come also with full odds, what are my chances that:

I will lose $200 without ever being up.

What about losing the $200 after being up a bit?

Quote: longtimelancer

I will win $100.
I will win $200.
I will win $1000.
I will win $2000.
I will win $10,000.

Your question is sort of meaningless without a stop condition for time/number of bets. Or, do you mean that you will either lose the $200 or reach a goal, no matter how long it takes, and you are asking really four questions, i.e.

lose $200 or win $100, no matter how long it takes
lose $200 or win $200, " " " " " "
etc. etc.

$10 DP and 3, 4, 5x odds is a lot of risk for a $200 BR, even without the DC bet(s).
For just the $10 DP with full odds, I ran a sim with $200 BR, $200 win goal.
Bust rate was 53.1%
win goal reached 46.9%

Trying to win $1000:
Bust rate was 84.5%
win goal reached 15.5%

Trying to win $2000
Bust rate was 91.6%
win goal reached 7.7%
max bets of 1600 reached .7% (my program requires a maximum number of bets, but I set it real high)

For a more realistic scenario, tell me how long you are willing to play before quitting, if you have neither busted nor reached your win goal.
Cheers,
Alan Shank

Quote: longtimelancer

Starting with $200 on a $10 table and playing the Don't Pass with full 345 odds and playing one Don't Come also with full odds, what are my chances that:
<snip> <snip>

yes, You had lots of answers before
the probabilities to hit a win goal given no time restraints will be abouts the same, adding DC just shortens the time to ruin/success

a simple way to estimate without any simulations/calculations is (for most simple bets)

(start bank/target bankroll) - (2* HE)

(it gets close most times and really who knows the difference in a session between 46.9% or 47.2%)

example:
turn $200 into $400

200/400= 0.50
HE = 1.40% * 2 = 2.8%
50% - 2.8% =

have fun!
Sally

Quote: longtimelancer

Last April I won over $2000 starting with $200 by playing the Don't with full odds (345) and playing 1 or 2 Don't Come with full odds. I am going back to Vegas this April and I wanted to try the same strategy and was wondering what my chances are.

Starting with $200 on a $10 table and playing the Don't Pass with full 345 odds and playing one Don't Come also with full odds, what are my chances that:

I will lose $200 without ever being up.
I will win $100.
I will win $200.
I will win $1000.
I will win $2000.
I will win $10,000.

Thanks!

P.S.: Mustang Sally was a great help last year with all of his calculations. I hope he is still here!

Without running the actual numbers and just looking at the facts, I'd say you got extremely lucky last time. Playing full 3-4-5 odds with a $10 DP/DC... If you take 2 DC points then your bankroll is essentially on the table each shooter. If you're allowed to wager double 3-4-5 from the don't (to get 3-4-5 odds) then that's even more! Let's take an "generic" roll... come out 6, you have $10 DP, $60 odds (to win $50... 5x). Then the next point is a 9, and you have your $10 DC, $60 odds (to win 4x). At this point you have 70% of your 'bankroll' on the table. While yes it might be a bit harder to re-throw a 6, then a 9, before the 7... If this happens, then you just lost a massive portion of your 'bankroll' on one shooter. Notice you originally said 1 or 2 DC bets. I'm rounding down to 1 for my example, so I assume you aren't actually taking max 3-4-5 odds, or the casino doesn't let you actually win max 3-4-5 odds (which most do, because that's what's mathematically right and what they're advertising).

Odds of 7: 6/36 = 1/6 = .16667 -- Resulting in total win of $110, which is 55% of your starting bankroll.
Odds of 6, then 7: (5/36) * (6/36) = .13889 * .16667 = .02315 -- Resulting in total loss of $20, which is 10% of your starting bankroll.
Odds of 9, then 7: (4/36) * (6/36) = .11111 * .16667 = .01852 -- Resulting in total loss of $10, which is 5% of your starting bankroll.
Odds of 6, then 9: (5/36) * (4/36) = .13889 * .11111 = .01543 -- Resulting in total loss of $140, which is 70% of your starting bankroll.
(note 9 then 6 is the same math)

So of all the rolls the shooter could throw that could effect you (after you've gotten your DP and 1 DC established):
16.7% of the time you'll win both.
2.3% of the time you lose the 6, win the 9.
1.9% of the time you lose the 9, win the 6.
3% of the time you lose both.

Again, this is all assuming you establish both points (when in reality your DP and DC bets are subjective to a disadvantage come out roll).

Quote: goatcabin

$10 DP and 3, 4, 5x odds is a lot of risk for a $200 BR, even without the DC bet(s).

but at the same time gives one of the highest chances of hitting the bankroll target
without single bet Bold Play, betting all $200 on one game/bet that is

BTW, Thanks for sharing the WCPro Risk of Ruin (by Steen) Don't Pass version

I do most of my simple RoR and target hitting calculations
in Excel
using a transition matrix and sometimes a recursive table.
I love Markov Chains and I do have a few programs that do them very quickly
but most can see and grasp the process when seen in a spreadsheet, in my opinion

Sally

snow snow snow

Quote: mustangsally

yes, You had lots of answers before
the probabilities to hit a win goal given no time restraints will be abouts the same, adding DC just shortens the time to ruin/success

a simple way to estimate without any simulations/calculations is (for most simple bets)

(start bank/target bankroll) - (2* HE)

(it gets close most times and really who knows the difference in a session between 46.9% or 47.2%)

example:
turn $200 into $400

200/400= 0.50
HE = 1.40% * 2 = 2.8%
50% - 2.8% =

have fun!
Sally

Something is fishy about this. The probability of reaching a win goal is mostly dependent on the variance. Clearly, the probability of doubling a $200 bankroll with a $10 DP bet (no odds) is nowhere near .472; my sim gives .243 for no odds, .42 for single odds, .457 for double odds, .472 for 3, 4, 5x. That formula does not take into account the odds bet.
Cheers,
Alan Shank

But the edge for full odds DP is .281% which would make your example 49.438%. Correct?

Quote: longtimelancer

But the edge for full odds DP is .281% which would make your example 49.438%. Correct?

Edge for DP, 3, 4, 5x is 0.37%, but my sims do not show that high a probability of winning $200.
It doesn't seem to me that this formula works, although for formula without the HE part does, i.e. for "fair" bets.
Cheers,
Alan Shank

.37% is for the pass 345x. The DP is .281% according to the Wizard.

Quote: longtimelancer

.37% is for the pass 345x. The DP is .281% according to the Wizard.

That must be counting the pushes in the bet handle, which I don't. However, the ev is the same, regardless. In the perfect 1980 (1925), the expected loss is 27 units, so 27 / 1980 = .013636, 27 / 1925 = .01403. No matter what the odds multiple, the ev is -27 in 1980 decisions.

In general showing a combined HA for flat bets with odds is misleading. The HA for the flat part is always the standard one, and the HA for the odds is zero; they should be regarded as separate, in my view. The ev is always the same, no matter the odds multiple, including zero.
Cheers,
Alan Shank

Quote: goatcabin

In general showing a combined HA for flat bets with odds is misleading

hmmm, that old debate.

can't dispute what you say about being separate, but it is also true you can't make the odds bet without the line bet. When crunching numbers, I'll agree you might as well toss out the odds bet in the calculation, unless you want to know the variance.

Quote: goatcabin

That must be counting the pushes in the bet handle, which I don't. However, the ev is the same, regardless.

Interesting. Using the formula EV= bet * HE , seems like you need an adjustment to "the bet" if you are going to get the same answer for the EV while changing the HE. Never thought about that before. Maybe this is actually a good argument against counting pushes, which I never liked either.

Quote: odiousgambit

hmmm, that old debate.

can't dispute what you say about being separate, but it is also true you can't make the odds bet without the line bet. When crunching numbers, I'll agree you might as well toss out the odds bet in the calculation, unless you want to know the variance.

The whole point of making odds bets is to increase your variance without increasing the expected loss.
For 60 bets:
$5 pass: ev -$4.24, SD $38.73
w/single odds: ev -$4.24, SD $75.84
w/double odds: ev -$4.24, SD $110.67
w/3, 4, 5x odds: ev -$4.24, SD $190.37
w/5 x odds: ev -$4.24, SD $228.15
w/10x odds: ev -$4.24, SD $418.63
w/100x odds: ev -$4.24, SD $3903.72

For the same ev, you get free variance. The lower the ev/SD, the less lucky you have to be to break even or better, the less unlucky you have to be to get slammed.

Quote: odiousgambit

Interesting. Using the formula EV= bet * HE , seems like you need an adjustment to "the bet" if you are going to get the same answer for the EV while changing the HE. Never thought about that before. Maybe this is actually a good argument against counting pushes, which I never liked either.

Exactly, but the ev, in my view, is primary and should be stressed. You lower the house edge, not by piling odds on top of a flat bet, but by reducing your flat bet and putting that money on odds. For example:

60 $20 pass bets: ev -$16.97, SD $154.90, handle $1200, rough probability of breaking even or better .4564
60 $5 pass bets, 3, 4, 5x odds: ev -$4.24, SD $190.37, handle $1133, rough probability of breaking even or better .4911
Cheers,
Alan Shank

Quote: goatcabin

Something is fishy about this.

downright stinks
I say
I could not find a table I had made for 345x odds. maybe later. just forget what I posted for now
I was cold

Quote: goatcabin

Clearly, the probability of doubling a $200 bankroll with a $10 DP bet (no odds) is nowhere near .472;
my sim gives .243 for no odds,
Cheers,
Alan Shank

this does not look right, clearly

to
double a
$200 bankroll =
36.32985871%
using the Gambler's Ruin Formula and p=949/1925
bankunits=200/10 (20 silly)

this also works too
=1/((q/p)^(bankunits)+1)

Sally

added at me lunch time
I also like color photos

I did this markov chain in Excel
shows all the bankrolls from 1 to 39 and ending either in 40 or 0 units bankroll
of course time is not included

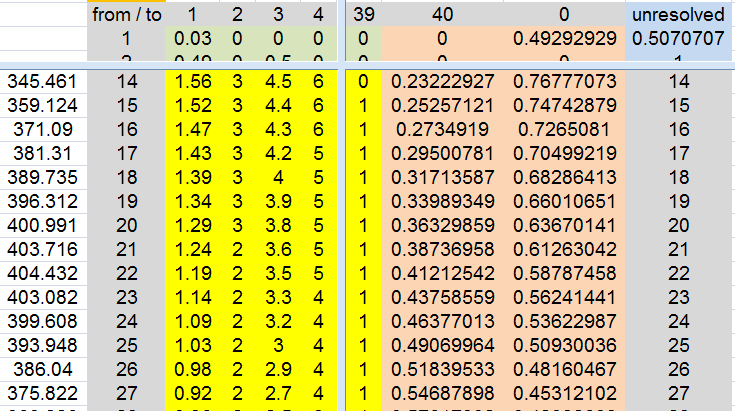
the average being the 400.991 value seen

here some values for the number of bets made (I have the exact distribution but I feel the world is not ready to view it in all it's beauty)
using a very simple (no simulation required) recursion table in Excel - yes, just add and multiply
pushes are counted as a bet made

resolved bets	prob success
50	0.002914017
100	0.031880577
200	0.113267684
300	0.179412431
400	0.228360401
500	0.264298663
999	0.342190982
1000	0.342256255
1500	0.358826069

a small view in me Excel
not proof I did it, but I could make a video of it for cash

Quote: odiousgambit

but it is also true you can't make the odds bet without the line bet.

this is absolutely a lie, in my opinion,
not true, 100% false
dotcom squared!

why, in my opinion, you tell lies?

I have many timessssssssssssssssssssss done this taking/laying odds and never was pointed out I could not do it... NEVER!
My friends did not even care!


I almost forgot

"all gamblers are liars (tell lies) but not all liars are gamblers"
quote from a famous gambler

Sally says so silly

Quote: mustangsally

to
double a
$200 bankroll =
36.32985871%
using the Gambler's Ruin Formula and p=949/1925
bankunits=200/10 (20 silly)

this also works too
=1/((q/p)^(bankunits)+1)

Sally

Yes, that's correct; I used $5 DP to get ~24%. With $10, my sim shows 36.3%, about the same in WinCraps Pro.
Can you elaborate on that formula, please?
Cheers,
Alan Shank

Quote: goatcabin

Yes, that's correct; I used $5 DP to get ~24%. With $10, my sim shows 36.3%, about the same in WinCraps Pro.
Can you elaborate on that formula, please?
Cheers,
Alan Shank

SN Ether
Doctrine of Chances book
page 243 I see this
(others have shown this too, even the Wizard, but his site is messed up, meaning all my links really do not work anymore there)


to double a 20 unit bankroll
(976/949)^20 +1 (one can use the complete fraction if wanted too)
then divide 1 by that value get the probability ;)

to double a 40 unit bankroll ($200/$5) what you did 1st
1 / (976/949)^40 +1

looks to come from a formula that was derived in the 1600s
sweet

Sally

Quote: longtimelancer

Starting with $200 on a $10 table and playing the Don't Pass with full 345 odds and playing one Don't Come also with full odds, what are my chances that:

I will lose $200 without ever being up.
I will win $100.
I will win $200.
I will win $1000.
I will win $2000.
I will win $10,000.

I will start showing probs for just 1 DP or DC bet at a time. This will set a base mark.
Then I will look for what I did before with multiple don't bets (I have a different computer with me on vacation)
I remember the success probs were very close, in other words, the number of don't bets did not matter, just the time (# of bets) differed

These were all simulated too (I can easily calculate these in Excel or using R, maybe later) 1 million sessions each
and most times target was exceeded.
Hitting target exactly will increase success rates, some a good amount (% wise)
=============================================
I will lose $200 without ever being up.(ever being up $10) >>16.700%
I will win $100. >>62.587%
I will win $200. >>47.102%
I will win $1000. >>15.351%
I will win $2000. >>7.927%
I will win $10,000. >>1.031%
=============================================
time not shown either (# or dice rolls or bets resolved)

what do you think are your chances?
you know you were lucky but not 1 in a million type luck
the odds are a very powerful bet to make
some think so (maybe Auntie Em), others think not (like the other Alan, Alan M... hehehe)

and how long on average do you think it will take.
Alan will like this part

extra credit Q:
what is the average bet for a $10 DPass always laying 345x Odds ($60 to win...)
hint: a point is established with a probability of 24/36

Sally

Quote: mustangsally

SN Ether
Doctrine of Chances book

to double a 20 unit bankroll
(976/949)^20 +1 (one can use the complete fraction if wanted too)
then divide 1 by that value get the probability ;)

to double a 40 unit bankroll ($200/$5) what you did 1st
1 / (976/949)^40 +1

looks to come from a formula that was derived in the 1600s
sweet

Sally

Thank you, thank you, thank you.
Cheers,
Alan Shank

Quote: mustangsally

extra credit Q:
what is the average bet for a $10 DPass always laying 345x Odds ($60 to win...)
hint: a point is established with a probability of 24/36

Show Spoiler

10/3 + 140/3 = 150/3
maybe too low?
some will say $70, yes they will
what is the truth?

Sally

How about, from the "Perfect 1980"?

10 x 660 = 6600
70 X 1320 = 92400
-----------
99000 / 1980 = 50.00

My program comes up with $51.14, because it uses 1925, i.e. not counting the pushes.
Cheers,
Alan Shank

Thank you! I travel at the end of April. I will let you know how it goes.

have fun when you play I say
win or lose

now if your take $200 two times (two squared = 2 times 2 = 2 plus 2)
try one of these the first attempt to double the $200

just flat bet and no odds
get some better comps for it I would think

$20.00 flat bets
43.03219130% = prob to hit $400
99.35579 = avg # of bets
335.40 = avg # of dice rolls

$40.00 flat bets
46.49901491%
24.96073
84.26

$50.00 flat bets
47.19756135% <<<< abouts the same as laying the odds
15.98428
53.96

Sally

Quote: mustangsally

why, in my opinion, you tell lies?

Is Sally trying to get my goat? Oh, pshaw, I'm used to it ...

what am I going to do when she makes me jealous though? It's a very rare occasion when I have had the opportunity to do the same thing [post free odds behind a player who isn't using his option], although sometimes I wonder if I should be more on the ball.