Thread Rating:
I will pay 3$ to paypal account for each question answered (or $50 for the whole kit and caboodle). However, I have to have some reassurance the answers are correct - perhaps verification from MathExtremist or Sally.
Anyway - here are the questions.
1) What is the probability (percentage) that a 10 will role 5 times before a 7 in 100 rolls? 1a) What about 4 times?
2) What is the probability that a 10 will role 5 times before a 7 in 1000 rolls? (assuming the answer to 1 is zero) 2a) What about 4 times?
3) How many times (with 95% confidence intervals or 2 STD) in 100 rolls will a 10 roll 5 times before a 7? 3a) or 4 times?
4) How many times (with 95% CI or 2 STD) in 1000 rolls will a 10 roll 5 times before a 7? 4a) or 4 times?
The next is harder to explain...let's see
5) After a 10 rolls once, what is the probability that a 4,5,6,8,9 (any combination) will roll 6 times before another 10 or a 7 rolls? 5a) What about 7 times? This is likely the same as asking what is the chance that a 4,5,6,8,9 rolls 6 (or 7) times before a 10 or 7.
6) After a 10 rolls twice, what is the probability 4,5,6,8,9 (or any combination) will roll 14 times before another 10 or a 7 rolls?
7) How many times in 1000 rolls can you expect that question 5 or 6 happens? In other words - lets assume that the answer to 4 is 3 times - so in 1000 rolls, a 10 rolls 5 times before a 7 three times. How many times in those 3 times could you expect that you would get a 4,5,6,8,9 rolling 7 or 14 times before the next 10? (I hope that made sense).
Oh, only one person gets the money.
Sheesh....
6) Likewise, exactly 14 times before a 10 or 7, the answer is 0.2%. At least 14 times, the answer is 0.68%.
Quote: phendricks5) If you want exactly six (and seven) times before a 10 or 7, the answers are 0.035 and 0.025. If you wanted at least six (or seven) times, the answers are 0.118 and 0.082.
6) Likewise, exactly 14 times before a 10 or 7, the answer is 0.002. At least 14 times, the answer is 0.0068
thanks.
and thanks for bringing up a point. I want to know "at least" instead of exactly. 11.8% sounds good.
I realize now I'm not sure I asked the question correctly.
I'll try again.
5) What is the chance of rolling a 4,5,6,8,9 six (or 7) times without rolling a 7, before two 10s?
Also, the next question is not worded correctly.
6) What is the chance of rolling a 4,5,6,8,9 fourteen times without rolling a 7 before 3 10s?
heheQuote: slackyhacky1) What is the probability (percentage) that a 10 will role 5 times before a 7 in 100 rolls? 1a) What about 4 times?
I know what you are ups two (or two squared). I have just a few moments until snow man time
it might just help you out
for at least 5 in a row (5+)
and at least 4 in a row (4+) in 100 rolls
Quote: slackyhacky2) What is the probability that a 10 will role 5 times before a 7 in 1000 rolls? (assuming the answer to 1 is zero) 2a) What about 4 times?
for at least 5 in a row (5+)
and at least 4 in a row (4+) in 1000 rolls
the others will have to wait for another day fur me (me eyes are tired)
burr fur
I love fur too
Sally
I think I got it right the 2nd time
Otherwise, a simple binomial formula would be sufficient.
Also, you cannot simply quarter the number of trials just because 25 and 250 are the expected number of 10's and 7's.
yes, It was useful as I did that also but did not show the results as a calculation I like much better.Quote: phendricksI believe the original poster is interested in 100 and 1000 rolls which include all outcomes (2 through 12). A simulation is probably most useful.
well that is what I did so here is the actual probability weightedQuote: phendricksOtherwise, a simple binomial formula would be sufficient.
Also, you cannot simply quarter the number of trials just because 25 and 250 are the expected number of 10's and 7's.
for the number of 10s and 7s from 0 to 100
Excel easy math for 5+ in 100 rolls
0.057960619
the error looks to me to be small
0.00006850718
I took this from me Excel
please check my work as my fingers were still cold
| # of 10s and 7s | run5+ prob | # of 10s and 7s prob | product |
|---|---|---|---|
| 0 | 0 | 3.2072E-13 | 0 |
| 1 | 0 | 1.06907E-11 | 0 |
| 2 | 0 | 1.76396E-10 | 0 |
| 3 | 0 | 1.92076E-09 | 0 |
| 4 | 0 | 1.55261E-08 | 0 |
| 5 | 0.004115226 | 9.93672E-08 | 4.08919E-10 |
| 6 | 0.006858711 | 5.24438E-07 | 3.59697E-09 |
| 7 | 0.009602195 | 2.34748E-06 | 2.2541E-08 |
| 8 | 0.012345679 | 9.0965E-06 | 1.12302E-07 |
| 9 | 0.015089163 | 3.09955E-05 | 4.67696E-07 |
| 10 | 0.017832647 | 9.40196E-05 | 1.67662E-06 |
| 11 | 0.020564842 | 0.000256417 | 5.27318E-06 |
| 12 | 0.023289509 | 0.00063392 | 1.47637E-05 |
| 13 | 0.02600665 | 0.001430384 | 3.71995E-05 |
| 14 | 0.028716264 | 0.002962939 | 8.50845E-05 |
| 15 | 0.031418351 | 0.005662506 | 0.000177907 |
| 16 | 0.034112912 | 0.010027354 | 0.000342062 |
| 17 | 0.036799977 | 0.016515642 | 0.000607775 |
| 18 | 0.039479567 | 0.025385154 | 0.001002195 |
| 19 | 0.042151702 | 0.036518993 | 0.001539338 |
| 20 | 0.044816404 | 0.04930064 | 0.002209477 |
| 21 | 0.047473692 | 0.062603988 | 0.002972042 |
| 22 | 0.050123588 | 0.074935076 | 0.003756015 |
| 23 | 0.052766112 | 0.084709217 | 0.004469776 |
| 24 | 0.055401285 | 0.090591801 | 0.005018902 |
| 25 | 0.058029126 | 0.091799692 | 0.005327056 |
| 26 | 0.060649658 | 0.088268934 | 0.005353481 |
| 27 | 0.063262899 | 0.080640755 | 0.005101568 |
| 28 | 0.065868869 | 0.070080656 | 0.004616134 |
| 29 | 0.068467591 | 0.057997784 | 0.003970969 |
| 30 | 0.071059082 | 0.045753808 | 0.003251224 |
| 31 | 0.073643365 | 0.03443835 | 0.002536156 |
| 32 | 0.076220457 | 0.024752564 | 0.001886652 |
| 33 | 0.078790381 | 0.017001761 | 0.001339575 |
| 34 | 0.081353155 | 0.011167823 | 0.000908538 |
| 35 | 0.083908799 | 0.007019775 | 0.000589021 |
| 36 | 0.086457334 | 0.004224864 | 0.000365271 |
| 37 | 0.088998779 | 0.002435958 | 0.000216797 |
| 38 | 0.091533154 | 0.001346187 | 0.000123221 |
| 39 | 0.094060478 | 0.000713364 | 6.70994E-05 |
| 40 | 0.096580771 | 0.000362627 | 3.50228E-05 |
| 41 | 0.099094053 | 0.000176891 | 1.75289E-05 |
| 42 | 0.101600342 | 8.283E-05 | 8.41555E-06 |
| 43 | 0.10409966 | 3.72414E-05 | 3.87682E-06 |
| 44 | 0.106592024 | 1.60815E-05 | 1.71416E-06 |
| 45 | 0.109077455 | 6.67085E-06 | 7.27639E-07 |
| 46 | 0.111555972 | 2.65867E-06 | 2.96591E-07 |
| 47 | 0.114027593 | 1.01821E-06 | 1.16105E-07 |
| 48 | 0.116492338 | 3.74759E-07 | 4.36566E-08 |
| 49 | 0.118950227 | 1.32568E-07 | 1.5769E-08 |
| 50 | 0.121401277 | 4.50731E-08 | 5.47193E-09 |
| 51 | 0.123845509 | 1.47298E-08 | 1.82422E-09 |
| 52 | 0.126282941 | 4.62666E-09 | 5.84268E-10 |
| 53 | 0.128713593 | 1.39673E-09 | 1.79778E-10 |
| 54 | 0.131137482 | 4.05223E-10 | 5.314E-11 |
| 55 | 0.133554628 | 1.12971E-10 | 1.50878E-11 |
| 56 | 0.13596505 | 3.02602E-11 | 4.11433E-12 |
| 57 | 0.138368766 | 7.78625E-12 | 1.07737E-12 |
| 58 | 0.140765795 | 1.92419E-12 | 2.7086E-13 |
| 59 | 0.143156155 | 4.56587E-13 | 6.53632E-14 |
| 60 | 0.145539866 | 1.04E-13 | 1.51362E-14 |
| 61 | 0.147916945 | 2.27323E-14 | 3.36249E-15 |
| 62 | 0.150287411 | 4.76645E-15 | 7.16338E-16 |
| 63 | 0.152651283 | 9.58335E-16 | 1.46291E-16 |
| 64 | 0.155008579 | 1.84679E-16 | 2.86268E-17 |
| 65 | 0.157359316 | 3.40946E-17 | 5.3651E-18 |
| 66 | 0.159703514 | 6.02682E-18 | 9.62505E-19 |
| 67 | 0.162041191 | 1.01946E-18 | 1.65195E-19 |
| 68 | 0.164372364 | 1.64913E-19 | 2.71071E-20 |
| 69 | 0.166697051 | 2.54938E-20 | 4.24974E-21 |
| 70 | 0.169015272 | 3.76337E-21 | 6.36067E-22 |
| 71 | 0.171327044 | 5.30052E-22 | 9.08123E-23 |
| 72 | 0.173632384 | 7.11644E-23 | 1.23564E-23 |
| 73 | 0.17593131 | 9.09865E-24 | 1.60074E-24 |
| 74 | 0.178223842 | 1.10659E-24 | 1.97221E-25 |
| 75 | 0.180509995 | 1.27873E-25 | 2.30823E-26 |
| 76 | 0.182789789 | 1.40212E-26 | 2.56292E-27 |
| 77 | 0.18506324 | 1.45674E-27 | 2.6959E-28 |
| 78 | 0.187330366 | 1.43184E-28 | 2.68227E-29 |
| 79 | 0.189591186 | 1.32914E-29 | 2.51992E-30 |
| 80 | 0.191845716 | 1.16299E-30 | 2.23115E-31 |
| 81 | 0.194093974 | 9.57196E-32 | 1.85786E-32 |
| 82 | 0.196335977 | 7.39298E-33 | 1.45151E-33 |
| 83 | 0.198571743 | 5.34432E-34 | 1.06123E-34 |
| 84 | 0.200801289 | 3.6053E-35 | 7.23948E-36 |
| 85 | 0.203024633 | 2.26215E-36 | 4.59272E-37 |
| 86 | 0.205241792 | 1.3152E-37 | 2.69934E-38 |
| 87 | 0.207452782 | 7.05472E-39 | 1.46352E-39 |
| 88 | 0.209657622 | 3.47392E-40 | 7.28333E-41 |
| 89 | 0.211856328 | 1.56131E-41 | 3.30774E-42 |
| 90 | 0.214048917 | 6.3609E-43 | 1.36154E-43 |
| 91 | 0.216235406 | 2.33E-44 | 5.03828E-45 |
| 92 | 0.218415813 | 7.59782E-46 | 1.65948E-46 |
| 93 | 0.220590153 | 2.17859E-47 | 4.80575E-48 |
| 94 | 0.222758445 | 5.40784E-49 | 1.20464E-49 |
| 95 | 0.224920705 | 1.13849E-50 | 2.56071E-51 |
| 96 | 0.227076949 | 1.97655E-52 | 4.48829E-53 |
| 97 | 0.229227195 | 2.71691E-54 | 6.22789E-55 |
| 98 | 0.231371459 | 2.77235E-56 | 6.41443E-57 |
| 99 | 0.233509758 | 1.8669E-58 | 4.3594E-59 |
| 100 | 0.235642108 | 6.22302E-61 | 1.4664E-61 |
| . | . | total | 0.057960619 |
so, I thinks my pics have answers that are close enough for SH
SH, I think I also answered your Q 3 and 4 also
ask questions if you likes
but now
sex, drugs (your choice) and rock-n-roll time
see ya all at the Super Bowl
Sally Oh
Love your math - but don't understand it.
I'll need some explanation how to interpret your spread sheet.
Tell me like I'm 10...
Quote: slackyhackyMustangsally,
Love your math - but don't understand it.
I'll need some explanation how to interpret your spread sheet.
Tell me like I'm 10...
You're not alone. I rarely understand anything she says. I think she's way smarter than me or something.
ZCore13
Quote: slackyhacky
1) What is the probability (percentage) that a 10 will role 5 times before a 7 in 100 rolls? 1a) What about 4 times?
Is this asking what is the probability of 10 coming up 5 times both within 100 rolls and before 7 comes up at all?
Without the 100 roll restriction, the probability of 10 coming up once before 7 is 1/3, so the probability of it happening five times is (1/3)5 = 1/243. Even with the 100 roll restriction, it's very close to 1/243, as the probability of any particular roll not being 7 or 10 is 3/4, so the probability of 96 of them not being 7 or 10 is (100)C(96) x (3/4)96, or about 1/250,000.
Similarly, for 4 times, it would be close to (1/3)4 = 1/81.
Quote: slackyhacky
2) What is the probability that a 10 will role 5 times before a 7 in 1000 rolls? (assuming the answer to 1 is zero) 2a) What about 4 times?
These are closer to 1/243 and 1/81 than in 1 and 1a.
Quote: ThatDonGuyCould you clarify some of the problems?
Is this asking what is the probability of 10 coming up 5 times both within 100 rolls and before 7 comes up at all?
I think you understand. If one thinks of a single turn in craps as starting with a 7, and ending with a 7 - what is the chance that one would get a 10 to roll five times in one turn.
That is the first part of understanding the question - but my real question is - how many times can one expect this to happen in 100 rolls? How about 1000 rolls?
q=ThatDonGuy]
Without the 100 roll restriction, the probability of 10 coming up once before 7 is 1/3,
I think it is 1/2.
The probability of a 10 is 8.3%, the probability of a 7 is 16.6%. Said another way, each time the dice is thrown, you are two times more likely to hit a 7 than a 10, right?
10 - 3 combinations = 3/36 = 8.3333%
7 = 6 combinations = 6/36 = 16.6666%
Quote: slackyhackyQuote: ThatDonGuy
Without the 100 roll restriction, the probability of 10 coming up once before 7 is 1/3,
I think it is 1/2.
The probability of a 10 is 8.3%, the probability of a 7 is 16.6%. Said another way, each time the dice is thrown, you are two times more likely to hit a 7 than a 10, right?
Yes - which means that 1/3 of the time, you will roll a 10 before a 7, and 2/3 of the time (i.e. twice as likely), you will roll a 7 before a 10.
For at least 5 10s before a 7 (for your lay 10 bet system)Quote: slackyhackyI'll need some explanation how to interpret your spread sheet.
Tell me like I'm 10...
a streak of 10s
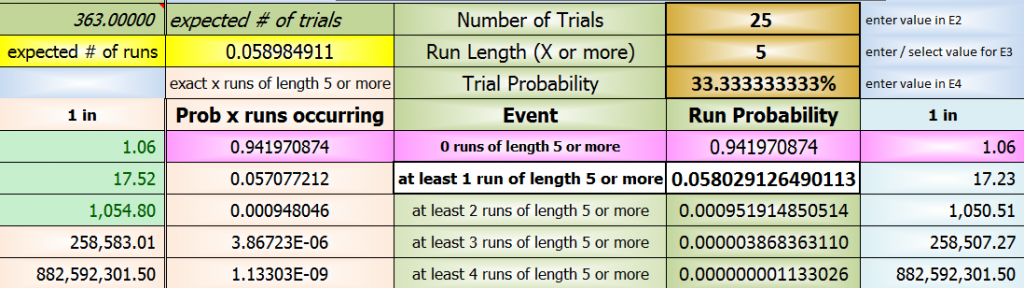
at least 1 run of length 5 or more
0.058029126490113
or
05.8029126490113%
find it in the first pic
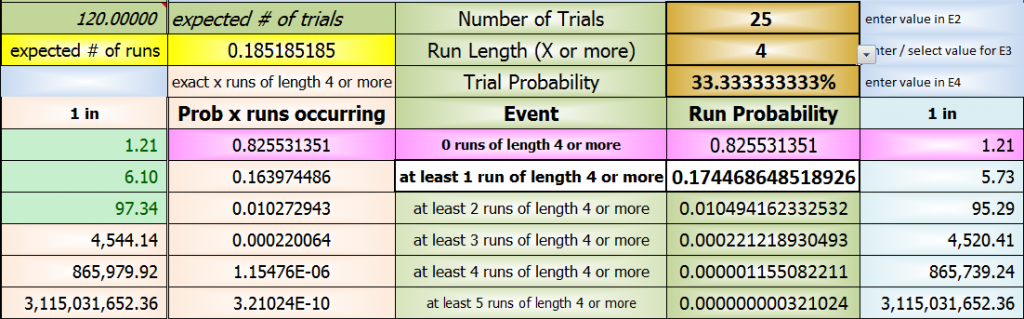
For at least 4 10s before a 7
at least 1 run of length 4 or more
0.174468648518926
or
17.4468648518926%
they are my answers
and are very accurate too for your needs
the number of trials I used was 25 (for your 100 dice rolls - why not 102?) because 100 * 9/36 = 25 and a direct calculation is just about what that value returns
the number of times are also shown in the pics
see if you can find them
the Excel spreadsheet is not in my online folder
maybe when I get times
Sally
snow time!
Thanks for the further explanation. I can see that.
I don't follow the rest of the numbers however.
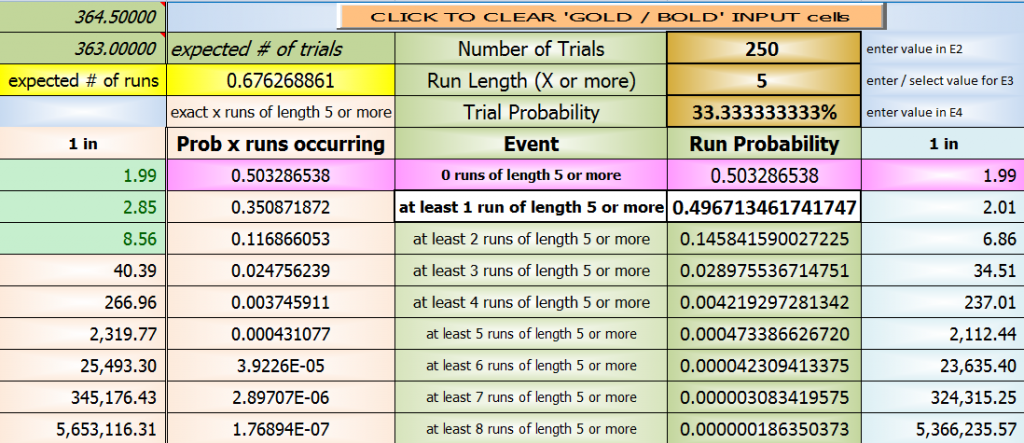
The yellow box is percent? Then for at least 5 in a row (in 1000 rolls), is 67% correct?
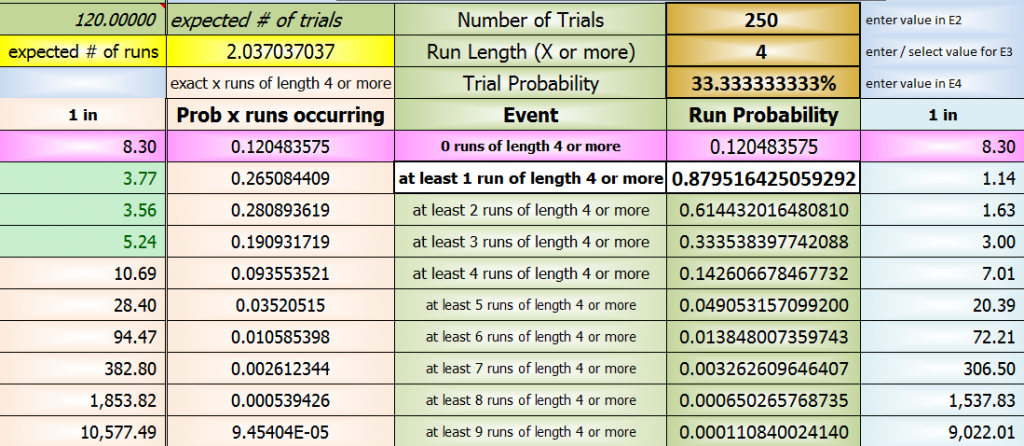
But the next one down (4 in a row for 1000 rolls) shows 204%. That doesn't make sense.
that value is found in cell C3 (B3 is the label)Quote: slackyhackyAlso, if there is a 17% chance a 10 will roll 4 times before a 7 in 100 rolls, can we say how many times can we expect that to happen in 100 rolls? 1000?
expected # of runs 0.185185185 (for 100 rolls)
that comes from the adding all the probabilities in cells E7:E11
or the sumproduct (the distribution) of cells C7:D11
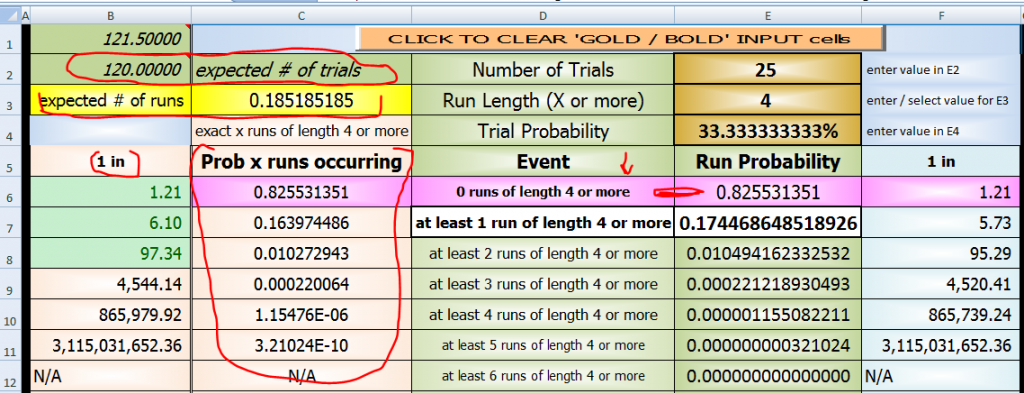
there are NO %Quote: slackyhackySally,
Thanks for the further explanation. I can see that.
I don't follow the rest of the numbers however.
The yellow box is percent?
it is not a %Quote: slackyhackyThen for at least 5 in a row (in 1000 rolls), is 67% correct?
it is an average of 0.67
and comes from the distribution below in pink
exactly 1 run: 0.350871872
exactly 2 runs: 0.116866053
exactly 3 runs: 0.024756239
and on down
It actually has it's own formula that I showed in another of my threads before
not a %Quote: slackyhackyBut the next one down (4 in a row for 1000 rolls) shows 204%. That doesn't make sense.
expected # of runs = 2.037037037
expected # of runs = a value >=0
probability is expressed as a value between 0 and 1 inclusive
I did not mean to make this into a lesson
I gave answers that I feel are very accurate, others do not feel that way
the universe is filled with opinions, really
hope this helps a little
you may be forced to simulate (maybe calculate too) everything yourself so you can then have another group of opinions too
more is fun!
Sally
Tons on this website seem like they could easily answer the question yet few offer...so really, thanks.
Want to tackle the other questions? :)
Quote: mustangsallyFor at least 5 10s before a 7 (for your lay 10 bet system)
a streak of 10s
at least 1 run of length 5 or more
0.058029126490113
or
05.8029126490113%
they are my answers
and are very accurate too for your needs
the number of trials I used was 25 (for your 100 dice rolls - why not 102?) because 100 * 9/36 = 25 and a direct calculation is just about what that value returns
Actually, there is a way to calculate an "exact" answer for #1 (which I misread - it should be, what is the probability of 10 being rolled since the most recent 7 (or before the first 7) at all within 100 rolls).
This is a state problem
Let P(a,b) be the probability of getting to the point where there are "b" 10s since the most recent 7 in "a" total rolls.
P(0,0) = 1
P(a,0) = P(a-1,0) x 3/4 + (P(a-1,0) + P(a-1,1) + P(a-1,2) + P(a-1,3) + P(a-1,4)) x 1/6
For 1 <= b <= 4, P(a,b) = P(a-1,b) x 3/4 + P(a-1,b-1) x 1/12
P(a,5) = P(a-1,4) x 1/12
For problem 1, we want the sum of P(5,5) + P(6,5) + ... + P(100,5), which, according to Excel, turns out to be 0.05796062, or 5.796062%.
For problem 2, we want the sum of P(5,5) through P(1000,5), which is 0.49634731, or 49.634731%.
Using a similar state problem, 1A is 17.3903047%, and 2A is 87.86884%.
3 and 4 can also be solved this way, but they are much harder to do as you need to include a third variable indicating how many times 5 or more in a row has already happened. This sort of problem is probably easier to solve with a Monte Carlo method (i.e. do many, many, many, manymanymany, many, did I mention many, many simulations).
this is basic mathQuote: slackyhackyThe next is harder to explain...let's see
5) After a 10 rolls once, what is the probability that a 4,5,6,8,9 (any combination) will roll 6 times before another 10 or a 7 rolls? 5a) What about 7 times? This is likely the same as asking what is the chance that a 4,5,6,8,9 rolls 6 (or 7) times before a 10 or 7.
6) After a 10 rolls twice, what is the probability 4,5,6,8,9 (or any combination) will roll 14 times before another 10 or a 7 rolls?
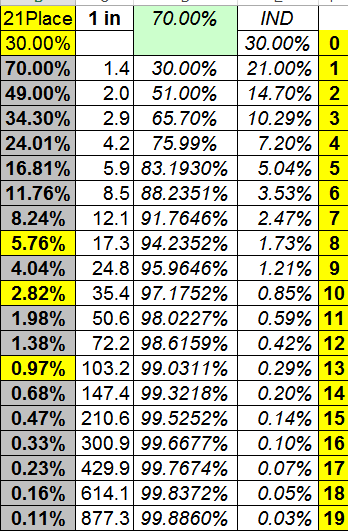
the 1st column is *at least* and the last is exactly X
there are 21 ways to roll the numbers you want (right?) and 9 you do not want
the prob of success = 21/30 (right?)
so the chance of getting at least 1 = 70% and exactly 1 = 21% as seen in the photo
for at least 2 in a row = .7 *.7 (we multiply)
(do you see why? both have to happen so we multiply independent and mutually exclusive events together - just the rules)
and I think you can take the rest from there
your version 2 Q5,6 may be different but I did not look at it that close
so I agree with another poster on the answers to Q5,6
Q7 looks simple, but no time now
back to snow
at least I can ski better than I throw a football or baseball (not by much!)
Sally says
who are the experts?
However, I need to know something. Do you want to *know* the answers or just *believe* the answers?
I don't want to get all epistemic on your ass, but in short: wouldn't you rather *know* how to calculate the answer yourself, and therefore have complete assurance that you have the correct answer? Instead of relying on someone else to calculate (or worse: simulate) the answer and then you have to rely on their authority?
Really, you shouldn't have a problem learning how to calculate the answers. No scary math needed; just basic arithmetic. I surmise from the excellent way you formulated the problems that you savvy basic arithmetic. :) And you really did a great job formulating the problems.
Just curious and *please* don't consider me hostile! Not! Just curious as to what motivates you and what would assure you that you have an authoritative answer. And why.
And no: you shouldn't trust any answer that I might give you. You don't know me. :)
Quote: ConcinnitySlackyhacky, I don't want your money (I charge a lot more than that; I consult for a living). No offense and I greatly appreciate the gesture as it implies a level of sincerity that I find missing in so many things in this lamentable world.
However, I need to know something. Do you want to *know* the answers or just *believe* the answers?
I don't want to get all epistemic on your ass, but in short: wouldn't you rather *know* how to calculate the answer yourself, and therefore have complete assurance that you have the correct answer? Instead of relying on someone else to calculate (or worse: simulate) the answer and then you have to rely on their authority?
Really, you shouldn't have a problem learning how to calculate the answers. No scary math needed; just basic arithmetic. I surmise from the excellent way you formulated the problems that you savvy basic arithmetic. :) And you really did a great job formulating the problems.
Just curious and *please* don't consider me hostile! Not! Just curious as to what motivates you and what would assure you that you have an authoritative answer. And why.
And no: you shouldn't trust any answer that I might give you. You don't know me. :)
Good questions.
I agree, I could probably work towards figuring it out on my own.
However, I have always struggled with stats. I got differential equations like a champ, but stats was like a foreign language written backwards. Also, people like yourself always overestimate how easy it is to understand and calculate because of how easy it comes to you.
Finally, I have grown to respect and trust the math wiz folks on here.
Ultimately, you are correct. I would much rather know how to do it than rely on having to ask the question but it is a matter of time and priorities in life.
My motivation? I have developed a way of betting that I have simulated over thousands and thousands of rolls and keep hitting the $100k mark starting at $16k. But since no system apparently works, I'm just trying to understand the math behind my betting.
Quote: slackyhackyGood questions.
I agree, I could probably work towards figuring it out on my own.
However, I have always struggled with stats. I got differential equations like a champ, but stats was like a foreign language written backwards. Also, people like yourself always overestimate how easy it is to understand and calculate because of how easy it comes to you.
Finally, I have grown to respect and trust the math wiz folks on here.
Ultimately, you are correct. I would much rather know how to do it than rely on having to ask the question but it is a matter of time and priorities in life.
My motivation? I have developed a way of betting that I have simulated over thousands and thousands of rolls and keep hitting the $100k mark starting at $16k. But since no system apparently works, I'm just trying to understand the math behind my betting.
Thank you! Great answers.
Please don't trust those simulations. I can give a long list as to why, but I suspect no one here cares. Simulations have value, but they never give the complete answer.
sometimes all one has is time but no way to even know how to startQuote: slackyhackyUltimately, you are correct. I would much rather know how to do it than rely on having to ask the question but it is a matter of time and priorities in life.
I have seen your system in code from what 7craps did for you.Quote: slackyhackyMy motivation? I have developed a way of betting that I have simulated over thousands and thousands of rolls and keep hitting the $100k mark starting at $16k. But since no system apparently works, I'm just trying to understand the math behind my betting.
I even saw his other systems where Lay 9 was used instead of Lay 10 and that doubled bankrolls more often and in less rolls, as I remember as I do not have the results to view.
turning $16k into $100k is about the same as turning $100 into $625
even a Marty can do that and have fun trying
but when the success probabilities are in the high 30% and low 40%
I would rather do something that gives closer to a 50% chance to double any starting bankroll
math is fun and
learning the math is more fun, I say so
Sally


