Craps question ( from someone who has only played craps once)

How likely is it to NOT win at least 2 bets IN A ROW within 12 decisions.

Lets say I choose Pass line and only pass line

I play at this table for a period of 12 pass/don't pass decisions.

What is the likelihood that I will not win back to back at least one time

I can lose 10 out of 12 bets as long as the 2 wins are back to back

Quote: richbailey86

How likely is it to NOT win at least 2 bets IN A ROW within 12 decisions.

Lets say I choose Pass line and only pass line

I play at this table for a period of 12 pass/don't pass decisions.

What is the likelihood that I will not win back to back at least one time

I can lose 10 out of 12 bets as long as the 2 wins are back to back

The probability of winning two in a row:

.4929 * .4929 = 0.24295041

Therefore, the probability of playing two Pass Line bets and losing one, the other, or both is .75704959.

If you look at twelve total PL bets, then you had the potential to win two in a row on eleven different occasions, because you couldn't have won two in a row STARTING with the twelfth bet.

1-(.75704959)^11 = 0.95318687703

Therefore, the probability that you will make eleven pairs of two bets and win at least two in a row once is 95.31869% and the probability that you will not win two in a row at all is 4.68131%.

thank you very much Mission, I appreciate you taking the time to answer that was great

No problem!

I did a brute force calculation, and got 9.8798%

Mission - are each of the 11 "pairs" necessarily independent, considering that each consecutive pair shares a result?

7craps had .0987 of no run with a similiar question

https://wizardofvegas.com/forum/gambling/craps/16060-beauty-of-probability/4/#post301921

Quote: bahdbwoy

7craps had .0987 of no run with a similiar question

https://wizardofvegas.com/forum/gambling/craps/16060-beauty-of-probability/4/#post301921

Thanks

Is OP creating a betting system?
I love them

Quote: ThatDonGuy

Mission - are each of the 11 "pairs" necessarily independent, considering that each consecutive pair shares a result?

I do not even know what mission came up with. His method to me loooooks to calculate the expected number of runs, or lack of them.
not any known probability in our universe, but we all could be wrong, yes?
maybe a new pair of shoes might help ;)

Quote: ThatDonGuy

I did a brute force calculation, and got 9.8798%

really? you listed all 2^12 outcomes and counted?
that is using the force, I say. I love brute or is that BRUT...
sounds the same to me but smells great, in me opinion

exercise is good for many too.


a streak calculator would be an easy solution and just subtract that value from 1 as most calcs figure the prob of at least 1 success.


How about the 14th Fibonacci number as a quick close answer?

it only works for 50% probs like a fair coin flip but it should give us the lowest probability as the pass line bet success rate is close to 49.3%, slightly lower than 50%
that # = 377 (can be found too in Pascal's triangle and who does not like triangles?)


377/2^12 = 377/4,096 or arounds about 0.092041016
Ah, mission was way off Houston (i was just there too)


Here, I solved this as did a 10 year old using very very simple simple math ands a spread sheet (I used excel)

Merry Christmas and Happy Holidays and Happy New Years
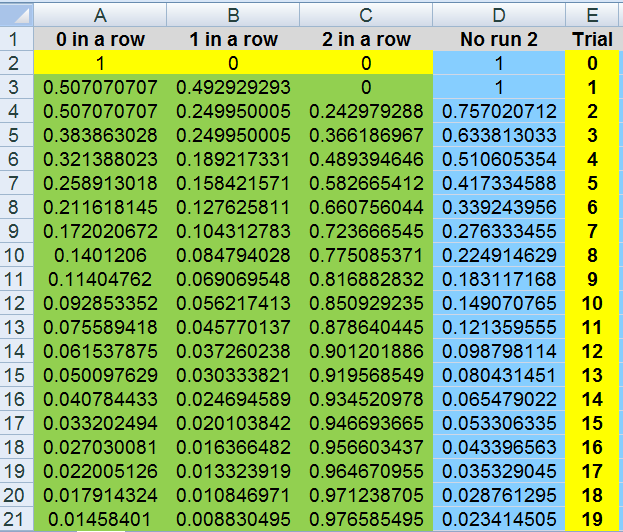
in cell D14 lies the gift

the cell formulas to do this yourself or is that elves


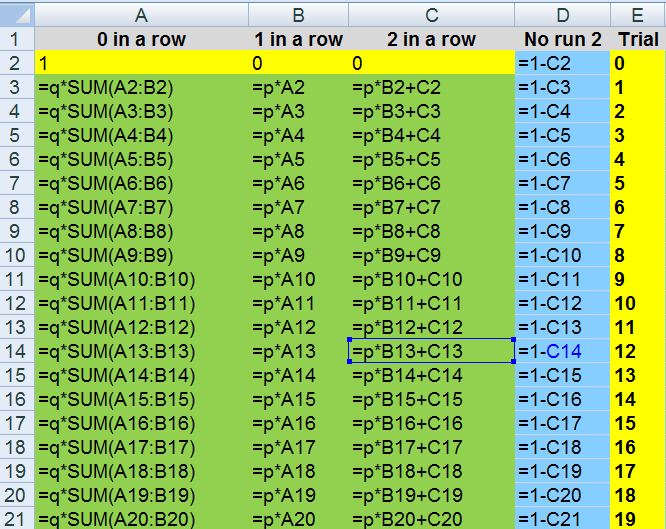
if you do not get it
just try it out
A2 to C2 are easy, just 1,0,0
A3 to D3 are easy too.
just fill them down (A3 to D3) how far you wants.
It really is up to yous

off to deliver the good and bad gifts this year
Sally says

Quote: mustangsally

really? you listed all 2^12 outcomes and counted?

Yes - I couldn't think of another way to calculate it accurately.

Well, "I" didn't count them - my 4.7GHz PC did.

Oh, and remember, you can use [sup] and [/sup] for superscripts - e.g. 2¹² instead of 2^12

Quote: ThatDonGuy

Yes - I couldn't think of another way to calculate it accurately.

Ah, Eye see
I figured wrong then, Me thought that you would do a simple Markov chain
like so

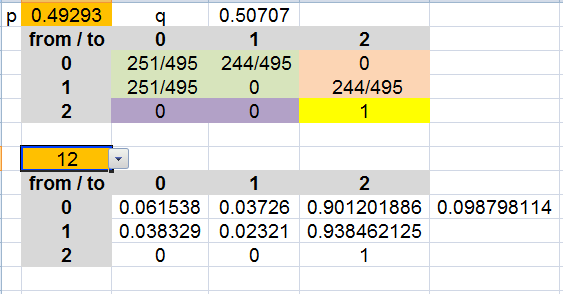
I use a udf
but P*P= P^2*P=P^3*P^2*P^2 would work innnnn Excel too, ugh

Quote: ThatDonGuy

Well, "I" didn't count them - my 4.7GHz PC did.

Oh, and remember, you can use [sup] and [/sup] for superscripts - e.g. 2¹² instead of 2^12

I was going to actually put 4,096 right from my win7 calc
but I was in a hurry as usual.
My calc uses 2^ and I like it.


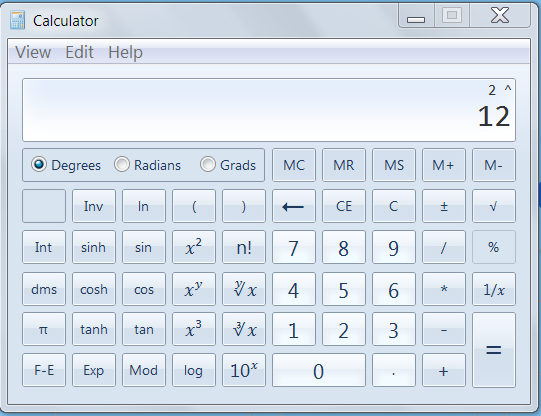
I still LOVE triangles!
Sally

almost forgot, for those that use R
(I do a lot)


that comes from the basic matrix program

U B Good

Quote: mustangsally

How about the 14th Fibonacci number as a quick close answer?

I noticed that, if P(n) is the probability of not getting two (or more) wins in a row over n trials with individual win probability = p:
P(1) = 1
P(2) = 1 - p²
P(n) = (1-p) P(n-1) + p(1-p) P(n-2), since if the first trial is a loss, the probability is the same as for n-1 trials, and if the first trial is a win, the second needs to be a loss, at which point the probability is the same as for n-2 trials

I tried deducing a recursive formula, but I noticed some strange patterns:
the p⁰ term = 1
the p¹ term = 0
the p² term = 1 - n
the p³ term = n - 2
the p⁴ term = (n - 4) (n - 3) / 2
the p⁵ term = - (n - 4)²

I did a matrix-based recursive solution, and got:

P(n) = ( (1 - p²) (J^n-1 - K^n-1) + JK (J^n-2 + K^n-2) ) / (J + K)
where J = sqrt(1 + 2p - 3p²) / 2 + (1 - p) / 2
and K = sqrt(1 + 2p - 3p²) / 2 - (1 - p) / 2

For n = 12 and p = 244/495, this returns 0.0987983465, so it "looks accurate".

Just don't ask about runs without streaks of 3 or more, as the mathematics becomes more and more complicated when doing it this way.
For example, for runs without streaks of 5:
P(n) = (1-p) P(n-1) + p (1-p) P(n-2) + p² (1-p) P(n-3) + p³ (1-p) P(n-4) + p⁴ (1-p) P(n-5)
The only way I know to solve this requires calculating the eigenvalues for a 5 x 5 matrix, which I think results in solving a quintic equation (which has been proven not to have a general solution).

Quote: ThatDonGuy

The only way I know to solve this requires calculating the eigenvalues for a 5 x 5 matrix, which I think results in solving a quintic equation (which has been proven not to have a general solution).

Looks to me you have fun doing lots of math and that is so cool

Here is a fast video I just did
on how I would do the run of 5 in Excel

has no sound or music
should slow it down to see cell entries if one wants
and full size if you wear glasses as I do at the computer

Sally




I currently love the MonaLisa Twins



and If you have come this far
the Excel workbook is in my onedrive folder
link to it in me blog
file name: excel-markov-chain-easy-stuff-streaks.xlsb

here is a video on how to expand a sheet to do another run size.
I went from 7 to 8
wow, I only started with 5 and now have 2 thru 8, with colors
imagine
my gift to all