Thread Rating:
Poll
 | 19 votes (51.35%) | ||
 | 6 votes (16.21%) | ||
 | 2 votes (5.4%) | ||
 | 2 votes (5.4%) | ||
 | 1 vote (2.7%) | ||
| No votes (0%) | |||
 | 1 vote (2.7%) | ||
| No votes (0%) | |||
 | 2 votes (5.4%) | ||
 | 4 votes (10.81%) |
37 members have voted
====================================
What roll is a craps shooter most likely to 7 out on?
(not crapless craps, that is another question)
I know it is out there
in other words,
what roll has the highest probability of being "the 7out roll"
given we have a NEW shooter that has just selected their two dice
======================================
btw, this is for all craps shooters (random, DI, RNG and machine)
also, the average number of rolls for a shooter's hand has been calculated close to 8.5
so that is not the answer
vote and what you thinks if you wants to
answer
the first come out roll by a new shooter is counted, even with a probability of 0 that it can be the 7out roll
so for those that did not count the first roll, then roll #2 is the roll.
But we do count the first roll because it is roll #1
1) #3
2) followed close by #2
3) in 3rd place is #4
the list
Top 10 rolls to 7out on in order
{3,2,4,5,6,7,8,9,10,11}
| Roll | 7out on |
|---|---|
| 0 | 0 |
| 1 | 0 |
| 2 | 0.111111111 |
| 3 | 0.116769547 |
| 4 | 0.104766804 |
| 5 | 0.091223629 |
| 6 | 0.078918038 |
| 7 | 0.068166764 |
| 8 | 0.058852758 |
| 9 | 0.05080065 |
| 10 | 0.043844137 |
| 11 | 0.037836136 |
the math in my last post on page 3
https://wizardofvegas.com/forum/gambling/craps/19743-what-roll-is-a-craps-shooter-most-likely-to-7-out-on/3/#post402565
takes you there
Sally
Quote:The average shooter throws the dice 8.53 times, including the seven-out roll. For more information on that, visit my odds table for the probability of every number of throws from 2 to 200.
I found my answers on my computer but is seems that one can also find the Wizard's table by searchingQuote: petroglyphI voted 3 and that includes the co roll, I believe ME answered it once but I can't find it either
"probability of a 7 out"
ok,
I would think a thread at WoV would show up
a start
For the probability of the 7out being the 2nd roll
it would be the chance of setting a point on the come out roll or the 1st roll
that is easy = 24/36 or 2/3
and the very next roll (the 2nd roll) being the 7 out (6/36 or 1/6) yea!
so 2/3 * 1/6 = 2/18 = 1/9 = abouts 11.11%
now to see if we can beat that and if yes, by how much
on to roll 3
after
the
Angles win Game #3
Sally
===================================================
added
for roll 2 and 3 it is not difficult to calculate the ways to 7 out
It gets wilder after 3, imo, so maybe that method should be the chance of not a 7 out on the Nth roll and subtract from 1
example
the sequences for roll 2 are easy
4,7
5,7
6,7
8,7
9,7
10,7
the number of ways (out of a total of 36*36)
4,7 = 3*6
5,7 = 4*6
6,7 = 5*6
8,7 = 5*6
9,7 = 4*6
10,7 = 3*6
= 144/1296
the sequences for 3 rolls that 7out on that 3rd roll are
2,4,7
2,5,7
2,6,7
2,8,7
2,9,7
2,10,7
3,4,7
3,5,7
3,6,7
3,8,7
3,9,7
3,10,7
4,2,7
4,3,7
4,5,7
4,6,7
4,8,7
4,9,7
4,10,7
4,11,7
4,12,7
5,2,7
5,3,7
5,4,7
5,6,7
5,8,7
5,9,7
5,10,7
5,11,7
5,12,7
6,2,7
6,3,7
6,4,7
6,5,7
6,8,7
6,9,7
6,10,7
6,11,7
6,12,7
7,4,7
7,5,7
7,6,7
7,8,7
7,9,7
7,10,7
8,2,7
8,3,7
8,4,7
8,5,7
8,6,7
8,9,7
8,10,7
8,11,7
8,12,7
9,2,7
9,3,7
9,4,7
9,5,7
9,6,7
9,8,7
9,10,7
9,11,7
9,12,7
10,2,7
10,3,7
10,4,7
10,5,7
10,6,7
10,8,7
10,9,7
10,11,7
10,12,7
11,4,7
11,5,7
11,6,7
11,8,7
11,9,7
11,10,7
12,4,7
12,5,7
12,6,7
12,8,7
12,9,7
12,10,7
==================================================
this sounds sound to meQuote: kenarmanIt would seem to me like it has to be the 2nd roll. Every roll after that would have already lost the number of rolls that went out on the 2nd roll and that seems at first glance to me like they would have to have lesser odds than the 2nd roll.
OK, because I have real $$$$.$$ bet on them Angels tonight, meaning I may not feel very well, mentally, if they play like they played the first 2 games of their Series
===========================================
for 3rd roll 7out
the sequences I listed in my last post add up to
5448
46656 = 36*36*36 (the number of ways the dice can roll in 3 rolls)
anyone care to do this a different way?
I have a few other ways too that work well
3rd roll = 5448 / 46656
oh,
1/9 = 5184 / 46656
agree?
Sally
So maybe you mean "at what point [roll], once point established, is the likelihood of 7-out greater than [say] 90% chance of having occurred on that roll or before"?
You roll an ordinary six-sided die once to determine the "point." You then keep rolling the die until you roll the point again. What is the expected number of total rolls? Although the mean is 7, the median is only 2.
That's kinda surprising since you specify 8.5 in the Ask The Wiz that I linked above.Quote: WizardI voted for 2.
Let's not forget that come out rolls of 2, 3, 7, 11 and 12 will occur 12 out of 36 times. Follow that with another 12/36 chance of a non-point roll, etc.
Although I agree that the way the question is posed, 8.5 doesn't sound right, I voted 4.
Bare with me for a sec:
7, the average number to be roll times 7 gets us forty nine.
Still with me?
7*7=49
Dice are cubes so that doesn't make sense.
RS doesn't like cubes. Circles and spheres are much better!
Still following?
According to my simulation, the number pi ~ 3.141592, often used in calculating dimensions on circles and spheres is the key.
7 * 7 * 3.141592 = 153.938008
My simulation wasn't able to round that complex number, so I had to do it by hand.
Oh what fun!
According to my math by hand, I rounded 153.938008 to get 154.
The shooter is most likely to 7 out on the 154'th roll.
Math fun!!
RS
from my first post hereQuote: odiousgambitsomebody has to explain to me what I am missing. Once the point has been established, <snip> <snip>
in other words,
what roll has the highest probability of being "the 7out roll"
given we have a NEW shooter that has just selected their two dice
or in other words,
the length of the shooter's hand
the probability of a seven-out on exactly that Nth roll
The shooter could do this
7,7,11,3,7, 7,7,7,12,11, 3,2,7,7,7, 4,5,6,7
one sequence, one shooter
the last 7 is the 7out = the 19th roll
Sally
Quote: eaglediceI voted 3. Just spent week in Las Vegas. Combination work and pleasure. I would say based on my many times at the craps tables, 3 was the magic number.
Just enough time to get your odds out there
Let N represent the roll number that sets the point that eventually falls to a 7-out. There may or may not have been prior rolls related to points that were made successfully or to non-point come-out rolls.
Let X represent a number of additional rolls after N. What is the probability that the 7-out occurs on roll N+X? I believe that it is:
P = (1/6) * (5/6)^(X-1).
It should be evident that this probability decreases uniformly with increasing X, so that the single highest probability is for X = 1, so that the 7-out occurs on roll N+1.
Now, the question is what value of N has the highest probability. Well, the probability that the very first roll sets the very first point number is 2/3. The probability that some later roll (call it roll Y) sets the very first point is:
P = (2/3) * (1/3)^(Y-1).
This, too, uniformly decreases with increasing Y, so the very first point is more likely to be set on the very first roll than on any other.
There is less than 50% probability that the first point is made successfully, with the probability dependent upon the point number. With that being the case, the second point has less than a 50% chance of even being established, much less being the point that is lost to a 7-out. The probabilities of the 3rd and subsequent points being the one that eventually loses is progressively less.
Thus, the single most likely case is that the very first roll sets a point (N = 1) and that the very next roll (X=1) is the 7-out. Thus, 2 rolls is the most likely outcome, though it is several rolls less than the average hand.
coolQuote: eaglediceI voted 3. Just spent week in Las Vegas. Combination work and pleasure. I would say based on my many times at the craps tables, 3 was the magic number.
sometimes it is hard to remember the last 3 rolls at any craps table (unless they were written down or one is playing "shoot to win craps")
reading the other posts in this thread it seems to me many misunderstood my question
this happens in casinos too
=================================
those that follow and the answers too soon,
what roll is the 7out roll
given the shooter has just selected their 2 dice and have not yet thrown their first come out roll
I said nothing about a point already being set
=================================
the reason for this thread is to show how easy it is to calculate the length of a shooters hand using simple math
and to point out my disagreements with
this website
http://www.timetravelsports.com/craps.html
(do not get me wrong, it is a nice read, but contains many errors, imo)
#1) " If the first roll is any point, and the second roll is a seven, then they have sevened-out and are finished.
However, rolling only twice is rare. Shooters regularly make dozens of rolls."
#2) "Simulations are needed to make an estimate."
ugh
Sally
Quote: ontariodealerI refused to answer because, stick change, waitress at the table and somebody spoke to the shooter are not on the choices.
+1
So if the chance is 1/6 on the second roll, its only 5/6 x 1/6 on the third, because you don't even get there 1/6 of the time. The very possibility of it happening on roll two reduces this conditional probability for subsequent rolls.
thank you for joining the discussion hereQuote: DraglineKind of a trick question, because if he sevens on roll #2, he never has an opportunity to seven out on the third or later roll.
now,
not at all
kind of a trick question
really a simple easy question
================================================
a craps shooter picks his 2 dice and faces his first come out roll
what roll (from 2 to 2,000,000,000,000) is the most likely roll to 7 out on?
================================================
craps players say the skill of the shooter determines the answer, but that is not true, imo, as each roll is an independent event
some also say to 7out on roll 2 is a rare event
===================================
I have shown the probabilities to 7out on the 2nd and the 3rd roll so far in other posts
summary
the 2nd roll is easy as the only sequences that qualify are these
4,7
5,7
6,7
8,7
9,7
10,7
because there are 36*36 = 1296 ways the dice can land in exactly 2 rolls
we can easily calculate the number of ways for each sequence
4,7 = 3*6 = 18
5,7 = 4*6 = 24
6,7 = 5*6 = 30
(18+24+30)*2 = 144 ways
so 144/1296
but all this math was not really needed as the case for 2 rolls is simply 2/3 * 1/6 = 2/18 = 1/9 = 11.11%
yesQuote: DraglineSo if the chance is 1/6 on the second roll,
you over-countingQuote: Draglineits only 5/6 x 1/6 on the third, because you don't even get there 1/6 of the time.
the first roll could be a 7 followed by 4,7 for example
well, roll 3 has a higher probability than roll 2 as I showed in another postQuote: DraglineThe very possibility of it happening on roll two reduces this conditional probability for subsequent rolls.
so your conclusion is not correct
every possible sequence is right here to 7out on that 3rd roll
2,4,7
2,5,7
2,6,7
2,8,7
2,9,7
2,10,7
3,4,7
3,5,7
3,6,7
3,8,7
3,9,7
3,10,7
4,2,7
4,3,7
4,5,7
4,6,7
4,8,7
4,9,7
4,10,7
4,11,7
4,12,7
5,2,7
5,3,7
5,4,7
5,6,7
5,8,7
5,9,7
5,10,7
5,11,7
5,12,7
6,2,7
6,3,7
6,4,7
6,5,7
6,8,7
6,9,7
6,10,7
6,11,7
6,12,7
7,4,7
7,5,7
7,6,7
7,8,7
7,9,7
7,10,7
8,2,7
8,3,7
8,4,7
8,5,7
8,6,7
8,9,7
8,10,7
8,11,7
8,12,7
9,2,7
9,3,7
9,4,7
9,5,7
9,6,7
9,8,7
9,10,7
9,11,7
9,12,7
10,2,7
10,3,7
10,4,7
10,5,7
10,6,7
10,8,7
10,9,7
10,11,7
10,12,7
11,4,7
11,5,7
11,6,7
11,8,7
11,9,7
11,10,7
12,4,7
12,5,7
12,6,7
12,8,7
12,9,7
12,10,7
if one does the math the same way as I did for the 2nd roll
and divide the total by 36*36*36
that should be
5448 / 46656 = 11.67695473251%
higher than roll 2 at 11.11%
both of my results match these here
https://wizardofodds.com/games/craps/number-of-rolls/
"The second column is the probability of a seven-out on exactly that roll"
and the 2nd article here
https://wizardofvegas.com/member/7craps/blog/
now on to roll 4 but with a different method
using the chance of the 4th roll NOT being a 7out
(and will show roll 2 and 3 too this way)
len-shooters-hand-recursive.xlsb
link in my blog
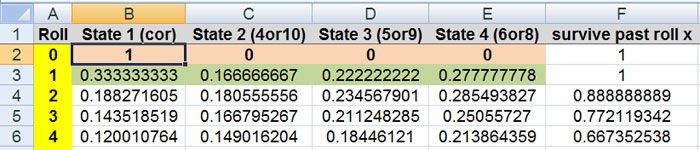
| Roll | State 1 (cor) | State 2 (4or10) | State 3 (5or9) | State 4 (6or8) | survive past roll x |
|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 0 | 1 |
| 1 | 12/36 | 6/36 | 8/36 | 10/36 | 1 |
| 2 | 0.188271605 | 0.180555556 | 0.234567901 | 0.285493827 | 0.888888889 |
Roll 0 = the shooter has selected the 2 dice for the come out roll but has not yet thrown them.
The 1 = that probability, the 3 point states are = 0
after roll#1
we now see the 4 probabilities for the 4 states the hand can be in
we must be in one of the 4 states with the stated probabilities.
(we are not considering a no-roll)
There are also transition probabilities to get to each state from roll to roll
It should be clear there are only two ways to get to a point state.
Either we came from a COR state at rollN-1 (the point was just established)
or we have remained in the point state (the roll was not a 7out or a point winner)
for row = roll 1
C3 = (6/36)*B2 + (27/36)*C2
(6/36)*B2 = the chance of rolling a 4 or 10 * the probability of being on the cor on the last roll
(27/36)*C2 = the chance of rolling any number except a 4,10,7 * the probability of being in that point state on the very last roll
D3 = (8/36)*B2 + (26/36)*D2
E3 = (10/36)*B2 + (25/36)*E2
for B3 we now have 4 ways to get to the cor
= (12/36)*B2 + (3/36)*C2 + (4/36)*D2 + (5/36)*E2
= we stay +we came from + we came from + we came from
F2 = the sum of B2 to E2
these cells get filled down to how far you want to go
I went to row 202
ok
this is done for me for now
I get bored quickly doing simple math
this was fun to a point
| Roll | 7out on |
|---|---|
| 0 | 0 |
| 1 | 0 |
| 2 | 0.111111111 |
| 3 | 0.116769547 |
| 4 | 0.104766804 |
| 5 | 0.091223629 |
| 6 | 0.078918038 |
| 7 | 0.068166764 |
| 8 | 0.058852758 |
| 9 | 0.05080065 |
| 10 | 0.043844137 |
| 11 | 0.037836136 |
===================================
imo,
it has been reported in the media that this problem is very difficult to calculate.
http://blogs.wsj.com/numbers/crunching-the-numbers-on-a-craps-record-703/
Some (including the Wizard of Odds who was in the news) used a simulation and some a Markov chain
Sally just used simple multiply and addition with the help of a spreadsheet
the world still has a long way to go to get to easy street for everyone
Sally
Quote: ontariodealerI refused to answer because, stick change, waitress at the table and somebody spoke to the shooter are not on the choices.
^ LMAO ^
Yeah .. the real answer is NEVER .. there is no roll you're ever more likely to roll a 7 .. each and every roll you only have a 1 in 6 chance of rolling 7 .. and a 5 in 6 chance of not rolling a 7! ;)
As for the answer of "how many rolls" until you roll a seven. The "average" would 6 .. since you always have a 1 in 6 chance. But obviously some of those rolls are forgotten because not too may people count 2,3,11,12 when there is a point and you're not playing Come bets or props. Then you also need to factor in "7 winners" on come out rolls after the previous roll was won (this is where you ask the Wizard to do his thing .. lol). And bla bla bla ... at the end of the day each roll you roll has a 1 in 6 chance of getting 7! Unless as Ontario Dealer forgot to mention .. it's a full moon on a Friday between 10 and 11 (am or pm doesn't really matter at this point)! ;)
Okay, that is 0.56 %.Quote: mustangsallythat should be 5448 / 46656 = 11.67695473251%
higher than roll 2 at 11.11%
Sally
So if I am out on the Strip panhandling so I can come in and get another twenty dollar buy-in, that 0.56 percent means twelve minutes less panhandling time.
But I think the chances of a 7-out increases with the more rolls each shooter has since a 7-out is inevitable. If you escaped a 7 out for the first 100 rolls the likelihood of a 7 out increases on the 101st roll, and so forth.
The practical advice is to use this data to know when to stop pressing and to start regressing.
Given everything else discussed here, as soon as the shooter starts smiling the 7 is coming.
I will take the hundred and then see what happens. smiling...
I tend to have a number of short rolls which don't bother me much, as long
as I understand what I am looking for, then when I see what I am looking for
I bet more and most nights I have enough rolls over 20 to make a reasonable return
on my time.
But over-all i would agree, 4-5 is most likely, if i make it past 5-6 i have a good chance to hit
20 or more rolls.
Dicesetter
Ask Al, the PB from Harrah's, if you don't believe me. But I made sure I was the only one at the table so I wouldn't cost anybody else any money. I tipped them well for the tutorial, but at the end, they said, "um, yeah, you're a darksider". I should be proud, I guess.
BTW, somebody was looking for crapless craps. Harrah's Gulf Coast has it, and it's usually open.
Quote: beachbumbabsI threw 12 PSO's in a row.
If somebody figures out that this is in the realm of 18 yo's in a row, just be quiet about it [g]
Quote: odiousgambitIf somebody figures out that this is in the realm of 18 yo's in a row, just be quiet about it [g]
Shhhh...lol.
1/6 each time, so this is easy [assuming that it is that easy]
I get about 1 in 2,176,782,137
Quote: odiousgambitnot taking my own advice, if the question is posed as "at the point of having set the point [which is what I think you mean] what are the odds of rolling a 7 next 12 times in a row?
1/6 each time, so this is easy [assuming that it is that easy]
I get about 1 in 2,176,782,137
They got progressively quieter (4 in the crew plus the PB) each time I did it. The stick was just standing there with his mouth open by the last couple.
My rolls were like this (don't recall what each point was by number, but the last 2 were 10-7)
3 8 7
7 4 7
10 7
6 7
7 12 5 7
8 7
8 7
9 7
2 6 7
9 7
10 7
10 7.
as far as throwing the dice, the rules are the same, you give them up after 7-out even as a darkside shooter
Quote: odiousgambitas far as throwing the dice, the rules are the same, you give them up after 7-out even as a darkside shooter
If you are the only player at the table, the dice come right back to you for a different hand. I think that was BBB's situation here, whether she was playing right side or dark side on individual hands.
Quote: DocIf you are the only player at the table, the dice come right back to you for a different hand. I think that was BBB's situation here, whether she was playing right side or dark side on individual hands.
Right. I waited to approach them until 3am, when the table was open but the players had left. They were stuck til 4am regardless, so I wasn't keeping them; they were fun to talk to. I overtipped on purpose, with 5 people working 1 minbet gambler and providing lots of advice, but my impression was they were enjoying giving advice to a newbie anyway. Not that they weren't paid to be there regardless, but I like playing with people who want to be there, not drabs waiting for the shift to end and resenting someone coming in and preventing them from closing.


