Poll
 | 3 votes (13.04%) | ||
 | 6 votes (26.08%) | ||
 | 4 votes (17.39%) | ||
 | 2 votes (8.69%) | ||
 | 6 votes (26.08%) | ||
 | 2 votes (8.69%) |
23 members have voted
she plans on no odds and will make a max 30 such bets over the course of a day, maybe in one hour or not.
Her choice (Pro Choice)
(yes, she could also have bought in for $30 and makes $10 bets, same ratios - same results)
=================================================
what do you think or feel is her chance to survive and NOT lose all her $300?
vote and/or explain the thought process
=================================================
Idea from:
This came from Help
WinCraps Classic
"How big a bankroll should you have? Well, having already stated that it should be no larger than what you can afford to lose, it depends on which bets you make, how large they are, and how long you intend to play.
If you intend to make $100 Pass Line bets with a $300 bankroll and expect to play for an hour, you're kidding yourself.
A typical table might see 100 dice rolls and 30 decisions per hour though it varies considerably.
Your bankroll could be a smoking hole in just a few short minutes! "
yes, could be
I have the answer from calculations and simulations (easy stuff)
39%
so I round up and say 40/60
starting with $400 and betting $100 for 30 bets we have basically a 50/50 chance
most underestimate the chances of a high probability wager
67% thought is was less than 25% or 1 in 4
I show some math in my 3rd post
I say 15% of the voters will get the right answer, maybe
Sally
Shooting from the hip, and given the poll options, that's what I would have selected. Although, if there had been a x>25% but 36%>x option, or 25%-36%, then I probably would have taken that. My initial thought on the matter (about 33%, again, just shooting from the hip) was not available in any of the ranges but was closer to 36% than 25%.
my husband only will allow me a max of 30 betsQuote: ThatDonGuyAssuming there are 36 come-outs per hour, I get surviving the hour 35.626% of the time.
that is the condition
all 30 bets do not have to be in one hour
am going to play tonight!
the Limo is here
Sally
so we look at this with Fleastiff's usual math averse way. Or to show his great knowledge: Maths averse way.
Since Hubby sends a Limo to take her to the casino, either Sally wins consistently or the Limo Driver promptly returns with Lola from the Naked Delicatessen. Since Sally is clearly bright enough to detect the aroma of Chips Vaingrainette, it seems the Limo must be a Positive Expectation and therefore Sally consistently win.
Now if first bet is one third of bankroll then surely Successful Sally must win often enough earn a Gross Return of 47.03983477794 percent.
QED
I would only know how to do simulations with wincraps, no maths.
simulation might take the fun out ... I'll guess. We know passline bets have a low standard deviation.
the fact she does not agree with Steen indicates a player will last longer than you might think.
I can't go higher than 25% in my gut but other considerations [skipping over Mission & Donguy posts] put it into ">36% but <50%"
simulations are allowed.Quote: odiousgambitI would only know how to do simulations with wincraps, no maths.
even online too
this one works well once you get java working
and all the watch-outs out of the way
the math can get difficult for different methods depending on one's math skills, imo
William Feller has two, even uses sine and cosine for exact calculations. ouch
Don Schlenger has one too that gives many times a very good approximation to exact calculations
But you can not do it in your head using the normal distribution, e and ouch!
even in Excel you have to be accurate 100%
to survive = 1- ruin
ruin =NORMSDIST((-B-ev)/sd) + EXP((-2*ev*B)/(sd^2)) * NORMSDIST((-B+ev)/sd)
One can use Matrix Algebra if they know how
Sally knows, but you have to raise the matrix to the power of 30 for my example
oh, oh
How about EV and SD?
sure, but you still have to use z-scores and ...
Oh,
maybe just a recursive method where we start with
300 with prob = 1
we know after 1 trial we can be at 200 with prob=q (1-p). 1*q
or at 400 with prob = p. 1*p
and the only way to get to 300 would be from 400 with q and 200 with p
this is basic multiplication and adding
after 2 trials
at 200 we can be at 100 with prob q or back to 300 with prob p
from 400 we can... hey this can get wild pretty fast
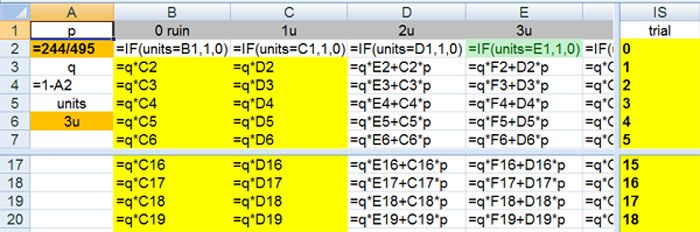
Maybe doing this in Excel we can tame that wild beast like this
the math is simple and 11 year olds, once shown, can do it too
the hidden cell formulas
Steen did not give an answer btwQuote: odiousgambitthe fact she does not agree with Steen indicates a player will last longer than you might think.
he only had that "you're kidding yourself"
here is how he finished his thoughts
the EV value was tried first
"Assuming worst case, that each bet you make will lose while you're waiting for that hot roll to come along, then to last an hour, your $300 bankroll could only endure bets as large as $10 ($10 bets times 30 decisions = $300 bankroll).
Of course realistically you'd be able to bet more and/or last longer since chances are you won't lose 30 bets in a row on the Pass Line.
Mathematically, on the Pass Line you can expect to lose an average of 1.41 cents for every dollar bet.
So betting $300 per hour you'd expect to lose an average of $4.23 per hour.
At that rate you might think that $300 would last for 3 days of non-stop play -
don't count on it."
Sally agrees here! another math problem to solve!!
yes!!!
"Perhaps one of the best ways to determine how much bankroll you'll need is to practice your strategy with WinCraps."
We knew he would say that
Sally says
How about math too!
"Just remember that each session can yield different results, so it may take many sessions to develop a good average.
So how long does your bankroll need to last to catch a hot roll?
Ah yes, the eternal quest of the craps player. The answer is as elusive as predicting what the next roll of the dice will be!"
ok
back to counting me winnings
Sally
Quote: mustangsallymy husband only will allow me a max of 30 bets
that is the condition
In that case, the chance of not losing the entire $300 is 39.06334036%
This appears to be a simple state problem:
S(a,b) is the probability of being ahead by "a" wins (note a can be zero or negative) after "b" comeouts
S(0,0) = 1
If p is the probability of winning, then, for a >= -1, S(a,b) = p x S(a-1,b-1) + (1-p) x S(a+1,b-1)
S(-2,b) = (1-p) x S(-1,b-1), since you would stop when reaching S(-3,b-1) as your bankroll is zero
S(-3,b) = S(-3,b-1) + (1-p) x S(-2,b-1)
S(-3,30) is the probability of losing at or before 30 comeouts, so the answer is 1 - S(-3,30)
well, wellQuote: ThatDonGuyIn that case, <snip> <snip>
My goal at the casino last night was to start with $300 and play a max number of bets (30) on the pass line at $100 each, no odds.
no one could believe I was attempting this for real.
The Dealers just laughed it off
well, I was also thinking if I hit $600 first before ruin I would stop
extra credit:
what were my chances of success?
rolling in the dough!
next time I will go all the way and make those 30 bets.
I had too much too eat and drink, so dancing was my medicine for the rest of the night
the results that look very close to Don in the lower matrix
the top matrix is the transition matrix
It reads from (left) to (top)
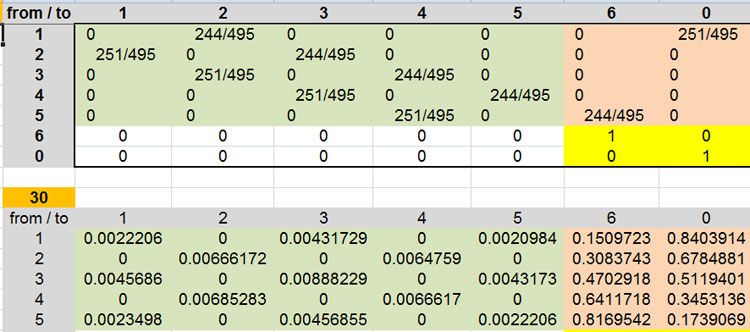
if someone wants an explanation
ask away!
Sally
Quote: mustangsallywell, I was also thinking if I hit $600 first before ruin I would stop
extra credit:
what were my chances of success?
I am assuming the stop limits are now 30 come-outs, $300 behind, or $300 ahead, in which case the probabilities are:
$300 behind: 0.5119400534
$200 behind: 0.0045685535
even: 0.0088822872
$200 ahead: 0.004317287
$300 ahead: 0.470291819
$100 behind and $100 ahead are impossible as the differences between your wins and losses would have to be 1, which is impossible if you play an even number of come-outs.
Quote: odiousgambitthe fact she does not agree with Steen indicates a player will last longer than you might think.
Did I miss something here? What doesn't she agree with?
The material Sally quoted from my help file was from a section titled "Discipline and Goals - Managing your Bankroll" and its purpose was not to convince the reader that making thirty $100 bets starting with a $300 bankroll would bring certain or swift ruin, but rather to make him think a little about the volatility of such an act and that it COULD bring certain or swift ruin and therefore might not satisfy his desire for action.
It's been said that a player's best chance to win is to employ a "maximum boldness" strategy. For example, wager your entire bankroll on one bet and then quit win or lose. Although we occassionally see people do this, is that what we normally see? I contend that many gamblers have a desire for action that cannot always be satisfied with one or a few wagers. They have a desire for the gambling experience, time at the table. So in essence, I was trying to get the reader to weigh his desire for action against the risk of ruin.
If our gambler wants to play the passline for an hour (about 30 bets) with a $300 bankroll, then he might find it useful to consider the risk of ruin:
| Bet Size | Risk of Ruin |
|---|---|
| $5 | 0 |
| $10 | 0.03% |
| $20 | 0.52% |
| $25 | 3.6% |
| $50 | 31% |
| $100 | 61% |
| $200 | 84% |
| $300 | 92% |
Note that these are just rough estimates based on some quick simulations with my riskofruin.bet file.
At $100 per bet, you can see there's a high probability of failure which is why I said you're kidding yourself (if you expect it to last.)
Quote: mustangsallySally says
How about math too!
Yes, of course the math, but there are a few reasons why a simulation may be preferable. One you said yourself: "the math can get difficult for different methods depending on one's math skills, imo" Another might be to get a feel for the action and another might be to play against specific roll files. You can probably think of a few more.
I'm not trying to suggest that spreading bets out is a mathematically superior way to play. I'm simply saying that a person should know his desires and limitations and bet accordingly.
I used 30 bets as we can be assured of that event happening sooner than later ;)Quote: SteenIf our gambler wants to play the passline for an hour (about 30 bets) with a $300 bankroll, then he might find it useful to consider the risk of ruin:
Bet Size Risk of Ruin $5 0 $10 0.03% $20 0.52% $25 3.6% $50 31% $100 61% $200 84% $300 92%
Note that these are just rough estimates based on some quick simulations with my riskofruin.bet file.
At $100 per bet, you can see there's a high probability of failure which is why I said you're kidding yourself (if you expect it to last.)
Here is your RoR table expanded with the calculated vales
please double-check your 1 unit RoR, seems way too high
(I used to enter data into a computer in a Biology lab - I have a Biology degree, and it was my job to enter only data that appeared "proper"
yes, some did not like me finding large errors in their data)
| Bankroll Units | Bet Size | Risk of Ruin - sim | Risk of Ruin | 1 in |
|---|---|---|---|---|
| 60 | $5 | 0 | 0 | n/a |
| 30 | $10 | 0.03% | (251/495)^30 | 704,602,733.3 |
| 15 | $20 | 0.52% | 0.64% | 155.26 |
| 12 | $25 | 3.60% | 3.48% | 28.73 |
| 6 | $50 | 31% | 30.54% | 3.27 |
| 3 | $100 | 61% | 60.94% | 1.64 |
| 2 | $150 | not run | 74.02% | 1.35 |
| 1.5 | $200 | 84% | n/a | n/a |
| 1 | $300 | 92% | 86.74% | 1.15 |
WoW!
Do you see what I see?
Only abouts an 87% chance of ruin betting your 1 unit bankroll.
I see this a lot Downtown Vegas, especially at the Plaza,
where some one walks to the table, from the bus depot,
buys in for $5, bets the pass line and they are still there 30 minutes later with a free drink and sometimes smiling!
Impressed I am
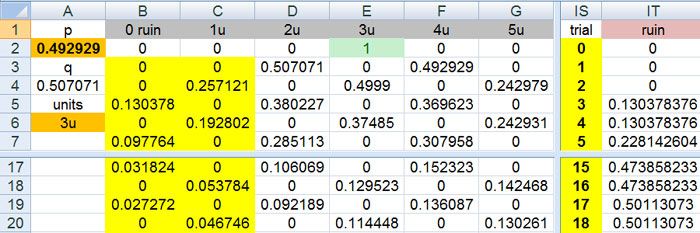
the data from my excel
in units (from / to Column)
| ruin | survive | from / to | ruin 1 in |
|---|---|---|---|
| 0.867368218 | 0.132631782 | 1 | 1.15 |
| 0.740191661 | 0.259808339 | 2 | 1.35 |
| 0.609366596 | 0.390633404 | 3 | 1.64 |
| 0.500003965 | 0.499996035 | 4 | 2.00 |
| 0.387503881 | 0.612496119 | 5 | 2.58 |
| 0.305400978 | 0.694599022 | 6 | 3.27 |
| 0.220942664 | 0.779057336 | 7 | 4.53 |
| 0.167194259 | 0.832805741 | 8 | 5.98 |
| 0.111903891 | 0.888096109 | 9 | 8.94 |
| 0.081320254 | 0.918679746 | 10 | 12.30 |
| 0.049859217 | 0.950140783 | 11 | 20.06 |
| 0.034811564 | 0.965188436 | 12 | 28.73 |
| 0.019332216 | 0.980667784 | 13 | 51.73 |
| 0.012977607 | 0.987022393 | 14 | 77.06 |
| 0.006440693 | 0.993559307 | 15 | 155.26 |
| 0.00416056 | 0.99583944 | 16 | 240.35 |
| 0.001815013 | 0.998184987 | 17 | 550.96 |
| 0.001129306 | 0.998870694 | 18 | 885.50 |
| 0.000423927 | 0.999576073 | 19 | 2,358.90 |
| 0.000254308 | 0.999745692 | 20 | 3,932.24 |
| 7.98224E-05 | 0.999920178 | 21 | 12,527.82 |
| 4.62125E-05 | 0.999953788 | 22 | 21,639.19 |
| 1.16383E-05 | 0.999988362 | 23 | 85,922.96 |
| 6.50905E-06 | 0.999993491 | 24 | 153,632.17 |
| 1.23262E-06 | 0.999998767 | 25 | 811,278.77 |
| 6.66604E-07 | 0.999999333 | 26 | 1,500,140.56 |
| 8.43483E-08 | 0.999999916 | 27 | 11,855,608.21 |
| 4.41502E-08 | 0.999999956 | 28 | 22,649,957.01 |
| 2.7989E-09 | 0.999999997 | 29 | 357,283,406.19 |
| 1.41924E-09 | 0.999999999 | 30 | 704,602,733.31 |
WoW!
Do you see what I see?
this time a 4 unit bankroll, $20 buy-in with $5 flat bets with no odds
has a 50/50 shot of making it to 30 bets done!
I also see this many times at the Plaza tooooooo!
I try that one too soon!
playing craps = FUN!
thank you Steen
Sally
added: a 40% success rate is still not bad, imo
Quote: mustangsallyI used 30 bets as we can be assured of that event happening sooner than later ;)Quote: SteenIf our gambler wants to play the passline for an hour (about 30 bets) with a $300 bankroll, then he might find it useful to consider the risk of ruin:
Bet Size Risk of Ruin $5 0 $10 0.03% $20 0.52% $25 3.6% $50 31% $100 61% $200 84% $300 92%
Note that these are just rough estimates based on some quick simulations with my riskofruin.bet file.
At $100 per bet, you can see there's a high probability of failure which is why I said you're kidding yourself (if you expect it to last.)
Here is your RoR table expanded with the calculated vales
please double-check your 1 unit RoR, seems way too high
Yes, you're right. I guess those last two estimates were a little bit too rough. I re-ran the sims for $200 and $300 a little longer and got 80% and 87% (still rough estimates but makes the point that the risk of ruin is quite high.) Of course the math provides the most accurate answer.
Quote: mustangsally(I used to enter data into a computer in a Biology lab - I have a Biology degree, and it was my job to enter only data that appeared "proper"
yes, some did not like me finding large errors in their data)
Bankroll Units Bet Size Risk of Ruin - sim Risk of Ruin 1 in 60 $5 0 0 n/a 30 $10 0.03% (251/495)^30 704,602,733.3 15 $20 0.52% 0.64% 155.26 12 $25 3.60% 3.48% 28.73 6 $50 31% 30.54% 3.27 3 $100 61% 60.94% 1.64 2 $150 not run 74.02% 1.35 1.5 $200 84% n/a n/a 1 $300 92% 86.74% 1.15
WoW!
Do you see what I see?
Only abouts an 87% chance of ruin betting your 1 unit bankroll.
Perhaps a little better than one might have guessed but remember that the risk of ruin can never hit 100% in this scenario and to drive it up into the 90's one would have to increase the bet size beyond one unit on wins.
Quote: mustangsallythank you Steen
My pleasure to contribute a few thoughts, but thank you too for your mathematical prowess.
Quote: mustangsallyadded: a 40% success rate is still not bad, imo
Not bad considering the size of the wagers relative to bankroll, but bad if the goal was to play for that full hour. In this case, the player who doesn't properly pace himself but still has a desire for the action feels pressure to replenish his stake and keep trying. In the end he's more likely than not to lose more than he bargained for. I'm not saying everyone does this but I see many who have and I point it out just as a caution. Also remember that success in this instance merely means making it past 30 bets without being wiped out. It does not mean turning a profit. I show (roughly) only a 29% chance of winning any money.
Few casinos actually look at a five dollar roulette bet and see twenty-six cents. Casinos make a whole heck of alot more on the pass line than 1.314.
Few players grind out the same five or ten dollar bet because if the player is lucky and gets ahead on those first few bets, he will want to raise his bets and play with "the casino's money".
this is what you meant 1.414%Quote: FleaStiffCasinos make a whole heck of a lot more on the pass line than 1.314
and really?
"a whole heck of a lot more"
How do you know that?
==============================
It is still a surprise to many (including me)
that if a player (say me) bought in for $20, flat bet $5 pass line (cocktails) and made a max of 30 bets (maybe an hour +/-)
(the closest $5 craps table to me is abouts an hour away)
I would have a 50/50 shot of success right from the START, that lasting 30 bets
not to mention my winnings too, I am Sally
I would say most all dealers and craps players would tell me
"Sally, you're kidding yourself"
why?
because they really do not know
in my opinion
and that is not a bad thing at all, not knowing that is
pay me 3:2 and I take your bet that I can survive 30 pass line decisions ands
we do it 100 times too
ah, now they want to know
Sally
Quote: mustangsallyI would have a 50/50 shot of success right from the START, that lasting 30 bets not to mention my winnings too,
Winnings? If any. You seem to define success as having been a grinder for 29 rolls and standing there with five bucks in your hands ready and prepared to make that 30th bet. As you plunk it down you declare "victory" even if that was your final five bucks and you just lost it.
Just as an aside, do you really play this way: avoiding ever "playing with their money" and raising your bet? Just grinding for one hour and departing?
heheQuote: FleaStiffWinnings? If any.
yes, ye of shown little knowledge in this area
some simple math, and simple simulations - except done by Ahigh,
imo,
can easily solve this, and of course I was ready with a $20 bankroll and a $15 bankroll.
The $15 is for Steen, I like him
You seem to say, without saying,
if any
want to put some probability on that?
what think ye? Flea?
<1%
<2%
<5%
<10%
<15%
<20%
cant be any higher than that right!
after your guess, I am assuming that is all I can get from you,
I will show some data and photos of my chances to walk with winnings above my $20 buy-in
All will be impressed I say
Think I will use WinCraps too, it has colors to show
29 decisions andQuote: FleaStiffYou seem to define success as having been a grinder for 29 rolls and standing there with five bucks in your hands ready and prepared to make that 30th bet. As you plunk it down you declare "victory" even if that was your final five bucks and you just lost it.
yes, success!
as per the conditions Steen and I talked about
I always play with my moneyQuote: FleaStiffJust as an aside,
do you really really really really really really really really really really really really really really really really play this way:
avoiding ever "playing with their money" and raising your bet? Just grinding for one hour and departing?
and I do raise my bets yes, especially when I know I am going to win my next bet
as to this system of a 4 unit bankroll,
I tried the 3 unit one this last weekend and doubled my units to 6 way before the 30th bet.
It was a BLAST!!
(my bets were $100 -impressed? should not be as I only had 3 units, same making $5 bets with $15 buy-in
all male craps players and dealers just do not get it. They are so impressed over nothing to be impressed abouts, imo)
I still have me winnings from the other night too
$300
see

Eyes are looking
only 3 units
Sally
Quote: RSWhat's the point of this thread, other than sally showing us she knows how to use wincraps?
The point of the thread is to belittle Fleastiff for being perpetually unacquainted with winnings.
However, don't hit that block button yet.... it seems there is a promise of some photos of Mustang Sally's bod in the offing.
[Serious] Please do not think that Fleasiff was trying to ridicule the terms of the earlier posting. Its simply that Fleastiff wished to point out that most people would not define as "a success" a session of five dollar grinding that winds up with the bankroll gone. [/Serious].
It is interesting to learn that such a five dollar grind on the pass line with no odds and no bet sizing has such a high percentage of
"NOT BEING A LOSS" (as opposed to winning).
Yes, Fleastiff admits he has little knowledge of winnings. Alas.
>some simple math,
Sorry ain't no such thing for Fleastiff as simple math.
>The $15 is for Steen, I like him
Lucky Steen.
>You seem to say, without saying, if any
say what without saying what?
>want to put some probability on that?
On what?
>what think ye? Flea?
'bout what?
<1%
<2%
<5%
<10%
<15%
<20%
cant be any higher than that right!
>after your guess, I am assuming that is all I can get from you,
Well, afterall, you are a married woman!
>I will show some data and photos of my chances to walk with winnings above my $20 buy-in
Okay, so its a 20 dollar buy in, what the bank roll? Min bet? Is it PassLine Only?
>All will be impressed I say
All will always be impressed with what you say.
>I always play with my money
but do you play with the casinos money?
>and I do raise my bets yes, especially when I know I am going to win my next bet
That is a heck of a lot better than Fleastiff's system of raising his bets only when he knows he is going to lose.
thank you SteenQuote: SteenAlso remember that success in this instance merely means making it past 30 bets without being wiped out. It does not mean turning a profit. I show (roughly) only a 29% chance of winning any money.
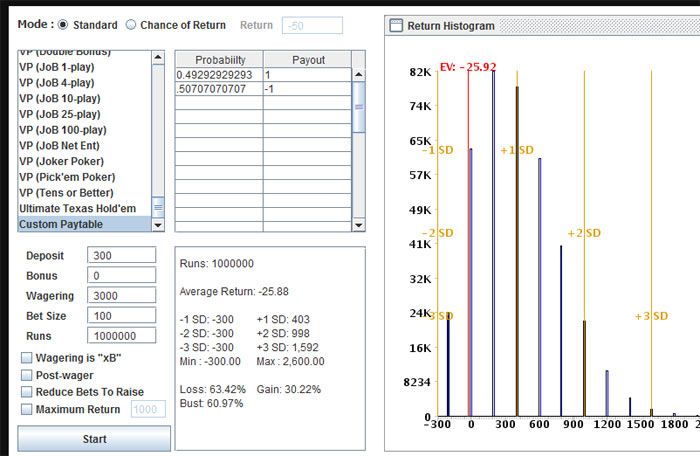
Here is what I show using no words
so it looks like you are very close (that close)

Sally is nice