August 15th, 2014 at 12:15:31 AM
permalink
Hi,
Can someone please explain me the calculation formula for "Small", Tall" and "All" win probability calculations?
Small bet wins if the shooter rolls a 2, 3, 4, 5, and 6 before rolling a seven - The probability as presented in the site are 0.026354
Tall bet wins if the shooter rolls an 8, 9, 10, 11, and 12 before rolling a seven - The probability as presented in the site are 0.026354
All bet wins if the shooter rolls a 2, 3, 4, 5, 6, 8, 9, 10, 11, and 12 before rolling a seven - The probability as presented in the site are 0.005258
Although the site presents the probability ,I'm interesting in the detailed calculation.
Thanks,
Dryfus
Can someone please explain me the calculation formula for "Small", Tall" and "All" win probability calculations?
Small bet wins if the shooter rolls a 2, 3, 4, 5, and 6 before rolling a seven - The probability as presented in the site are 0.026354
Tall bet wins if the shooter rolls an 8, 9, 10, 11, and 12 before rolling a seven - The probability as presented in the site are 0.026354
All bet wins if the shooter rolls a 2, 3, 4, 5, 6, 8, 9, 10, 11, and 12 before rolling a seven - The probability as presented in the site are 0.005258
Although the site presents the probability ,I'm interesting in the detailed calculation.
Thanks,
Dryfus
August 15th, 2014 at 12:54:07 AM
permalink
HiQuote: DryfusHi,
Although the site presents the probability ,I'm interesting in the detailed calculation.
try here
https://wizardofvegas.com/forum/gambling/craps/17175-new-all-high-all-low-casino-craps-prop-bet/2/#post332587
There are many methods that work.
Some more challenging than others depending on your math skill level
I did not yet add the all small/all tall matrix/recursion solution (I have them completed)
There are 1022 possible states the ALL can be in plus 3 more for 0, fail and success
we just fill in the transition probabilities and sum the products (a little more involved actually)
only 30 states for small/tall plus 3 more for 0, fail and success
by states, I mean the number of numbers hit starting with 0
we could hit just 1# 10C1 = 10 so there are 10#s that can be the first #
now, having the 1st we want a second and there are
10C2 = 45 possible combinations (where order does not matter)
like so and we can calculate the probabilities of moving from each of the first 10 states to these 45 states
and so on. lots of math
10C3 = 120 possible 3# combos
10C4 = 210
10C5 = 252
10C6 = 210
10C7 = 120
10C8 = 45
10C9 = 10
Hey looks like Pascal's Triangle
we could hit just 1# 10C1 = 10 so there are 10#s that can be the first #
now, having the 1st we want a second and there are
10C2 = 45 possible combinations (where order does not matter)
like so
2,3
2,4
2,5
2,6
2,8
2,9
2,10
2,11
2,12
3,4
3,5
3,6
3,8
3,9
3,10
3,11
3,12
4,5
4,6
4,8
4,9
4,10
4,11
4,12
5,6
5,8
5,9
5,10
5,11
5,12
6,8
6,9
6,10
6,11
6,12
8,9
8,10
8,11
8,12
9,10
9,11
9,12
10,11
10,12
11,12
and so on. lots of math
10C3 = 120 possible 3# combos
10C4 = 210
10C5 = 252
10C6 = 210
10C7 = 120
10C8 = 45
10C9 = 10
Hey looks like Pascal's Triangle
Maybe if get some time, it is Friday,
I can clean up my Excel workbooks and link to them online
Once you see how it it done, it is quite easy IMO, just a bunch bunch of calculations that a computer can do lickety–split
Sally
I also forgot to mention we can just list all the permutations of the winning sequences (small/tall for example)
5! = 120 of them
2 3 4 5 6
2 3 4 6 5
2 3 5 4 6
2 3 5 6 4
2 3 6 4 5
2 3 6 5 4
2 4 3 5 6
2 4 3 6 5
2 4 5 3 6
2 4 5 6 3
2 4 6 3 5
2 4 6 5 3
2 5 3 4 6
2 5 3 6 4
2 5 4 3 6
2 5 4 6 3
2 5 6 3 4
2 5 6 4 3
2 6 3 4 5
2 6 3 5 4
2 6 4 3 5
2 6 4 5 3
2 6 5 3 4
2 6 5 4 3
3 2 4 5 6
3 2 4 6 5
3 2 5 4 6
3 2 5 6 4
3 2 6 4 5
3 2 6 5 4
3 4 2 5 6
3 4 2 6 5
3 4 5 2 6
3 4 5 6 2
3 4 6 2 5
3 4 6 5 2
3 5 2 4 6
3 5 2 6 4
3 5 4 2 6
3 5 4 6 2
3 5 6 2 4
3 5 6 4 2
3 6 2 4 5
3 6 2 5 4
3 6 4 2 5
3 6 4 5 2
3 6 5 2 4
3 6 5 4 2
4 2 3 5 6
4 2 3 6 5
4 2 5 3 6
4 2 5 6 3
4 2 6 3 5
4 2 6 5 3
4 3 2 5 6
4 3 2 6 5
4 3 5 2 6
4 3 5 6 2
4 3 6 2 5
4 3 6 5 2
4 5 2 3 6
4 5 2 6 3
4 5 3 2 6
4 5 3 6 2
4 5 6 2 3
4 5 6 3 2
4 6 2 3 5
4 6 2 5 3
4 6 3 2 5
4 6 3 5 2
4 6 5 2 3
4 6 5 3 2
5 2 3 4 6
5 2 3 6 4
5 2 4 3 6
5 2 4 6 3
5 2 6 3 4
5 2 6 4 3
5 3 2 4 6
5 3 2 6 4
5 3 4 2 6
5 3 4 6 2
5 3 6 2 4
5 3 6 4 2
5 4 2 3 6
5 4 2 6 3
5 4 3 2 6
5 4 3 6 2
5 4 6 2 3
5 4 6 3 2
5 6 2 3 4
5 6 2 4 3
5 6 3 2 4
5 6 3 4 2
5 6 4 2 3
5 6 4 3 2
6 2 3 4 5
6 2 3 5 4
6 2 4 3 5
6 2 4 5 3
6 2 5 3 4
6 2 5 4 3
6 3 2 4 5
6 3 2 5 4
6 3 4 2 5
6 3 4 5 2
6 3 5 2 4
6 3 5 4 2
6 4 2 3 5
6 4 2 5 3
6 4 3 2 5
6 4 3 5 2
6 4 5 2 3
6 4 5 3 2
6 5 2 3 4
6 5 2 4 3
6 5 3 2 4
6 5 3 4 2
6 5 4 2 3
6 5 4 3 2
then calculate the probabilities for each and add them up
another snap shot in Excel for small/tall
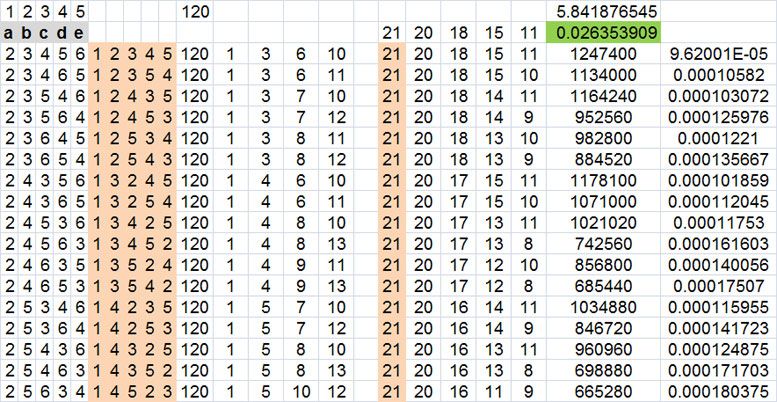
examples
23456 = 120/1,247,400
23465 =120/1,134,000
the denominator is what changes for each different sequence
because from the starting 21 ways the bet could be resolved (win or loss)
it gets smaller with each number hit
do you see why?
Okay...
the All requires 10! calculations (3,628,800) using this method (oh, actually not as 2,3,4,5,6,8,9,10,11,12 and 12,3,4,5,6,8,9,10,11,2 have the same probabilities. I have to look closer into this too) and I just did (fri afternoon)
3,628,800 /2^5 = 113,400 unique permutations (32 ways for each) and I have a unique permutation generator for the free program R
sure Excel could do this too
this method should be avoided unless you just let a computer do it for you, as I did.
can not even imagine doing this by hand
here is the snapshot and the probability is the same as all the other methods that have been used
calculus, inclusion-exclusion (R and Excel), Matrix Algebra, recursion and summing permutation probabilities
WOW!
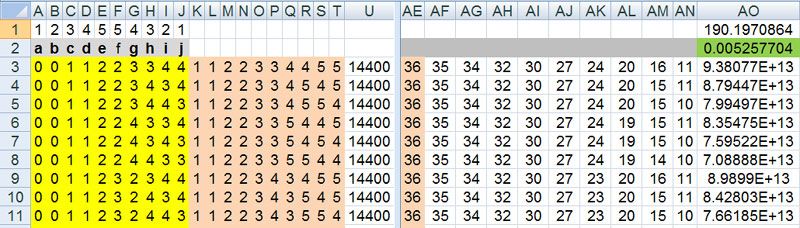
the sequences used 0 for 2 and 12
1 for 3 and 11 and so on
I guess I can explain every method if you have a request for a favorite one, except the calculus one
I just can't do everything
but watch out for what I do accomplish
Sally
I Heart Vi Hart
August 15th, 2014 at 11:59:47 PM
permalink
Hi Sally,
Wow! never imagine to get such good explanation, thanks!
BTW, I've ran simulation in R and got nice approximations for these probabilities:
Code:
Here are the simulation results of 100,000 Iterations:
Again, thank you very much for your answer,
Dryfus
Wow! never imagine to get such good explanation, thanks!
BTW, I've ran simulation in R and got nice approximations for these probabilities:
Code:
Iterations=100000
Craps <- matrix(0,nrow=Iterations,ncol=11)
colnames(Craps) <- c(2:12)
Results <- matrix(0,nrow=2,ncol=3)
colnames(Results) <- c("Small","Tall","All")
rownames(Results) <- c("Frequency","Probability")
for (i in 1:Iterations)
{
Roll=0
while (Roll!=7)
{
Roll <- sum(sample(c(1:6),2,replace=TRUE))
Craps[i,toString(Roll)] <- Craps[i,toString(Roll)]+1
}
#Small (rolls 2,3,4,5,6 before 7)
if (prod(Craps[i,1:5])>0)
Results[1,"Small"]=Results[1,"Small"]+1
#Tall (rolls 8,9,10,11,12 before 7)
if (prod(Craps[i,7:11])>0)
Results[1,"Tall"]=Results[1,"Tall"]+1
#All (rolls 2,3,4,5,6,8,9,10,11,12 before 7)
if (prod(Craps[i,1:11])>0)
Results[1,"All"]=Results[1,"All"]+1
i=i+1
}
Results[2,]=Results[1,]/Iterations
format(Results,scientific=FALSE)
Here are the simulation results of 100,000 Iterations:
| Small bet Win | Tall bet Win | All bet Win | |
|---|---|---|---|
| Frequency | 2,615 | 2,606 | 503 |
| Probability | 0.02615 | 0.02606 | 0.00503 |
Again, thank you very much for your answer,
Dryfus
August 16th, 2014 at 11:07:27 AM
permalink
yes simulations can work too, nice they areQuote: DryfusAgain, thank you very much for your answer,
Dryfus
and thank you
it was fun and I got a chance to finish my bonus craps projects too :)
I got this running your sim one time (about 50 seconds time)
Small Tall All
Frequency 2.638e+03 2.564e+03 5.14e+02
Probability 2.638e-02 2.564e-02 5.14e-03
The fastest way IMO to solve these type of questions (if you do or do not understand the math behind the bet)
is to use the code I linked to
in R for any subset
it is done before you know it
Sally
> ##################################################################
> # Odds against rolling a subset of numbers before a single number - The All bet
> ##################################################################
> nums = c(2,3,4,5,6,8,9,10,11,12,7) # Last must occur only after all others in any order
>
> in_36 = ifelse(nums <= 7, nums-1, 13-nums) # Ways to make each number
> i = length(in_36)
> p = 0
> for (j in 1:(i-1)) { # Last number before j numbers
+ terms = combn(in_36[1:(i-1)],j) # Matrix w/combos of j numbers in C(i-1,j) columns
+ for (k in 1:ncol(terms)) { # Sum each column, compute and add probabilities
+ p = p + (-1)^(j+1) * in_36/(in_36 + sum(terms[1:j,k]))
+ }
+ }
> p1 = (1-p)
> p1
[1] 0.005257704
> ch = 1/(1-p)
> ch
[1] 190.1971
> Odds.to.1 = 1/(1-p) - 1
> Odds.to.1
[1] 189.1971
> ##################################################################
> # Odds against rolling a subset of numbers before a single number - Small or Tall
> ##################################################################
> nums = c(2,3,4,5,6,7) # Last must occur only after all others in any order
>
> in_36 = ifelse(nums <= 7, nums-1, 13-nums) # Ways to make each number
> i = length(in_36)
> p = 0
> for (j in 1:(i-1)) { # Last number before j numbers
+ terms = combn(in_36[1:(i-1)],j) # Matrix w/combos of j numbers in C(i-1,j) columns
+ for (k in 1:ncol(terms)) { # Sum each column, compute and add probabilities
+ p = p + (-1)^(j+1) * in_36/(in_36 + sum(terms[1:j,k]))
+ }
+ }
> p1 = (1-p)
> p1
[1] 0.02635391
> ch = 1/(1-p)
> ch
[1] 37.94503
> Odds.to.1 = 1/(1-p) - 1
> Odds.to.1
[1] 36.94503 I Heart Vi Hart
July 5th, 2018 at 10:39:42 AM
permalink
The following Python code computes the odds exactly. The basic idea is that the probability of rolling one set of numbers before another is the sum of rolling each number first then rolling the rest before the other set. So, for example, the probability of rolling both a 2 and a 3 before a 7 is the probability of rolling a 2 before a 3 or a 7 times the probability of rolling a 3 before a 7 plus the probability of rolling a 3 before a 2 or a 7 times the probability of rolling a 2 before a 7. That is,
P({2,3} before {7}) = P({2} before {3,7}) * P({3} before {7}) + P({3} before {2,7}) * P{{2} before {7})
When the set you want has just one number, the probability of rolling it before the set of other numbers is the number of ways to make the one number divided by the number of ways to make that number plus the others. So, for example, P({2} before {3,7}) = 1 / (2 + 6) = 1 /8.
The exact probabilities produced by the program are P(small) = P(tall) = 20049/760760 and P(all) = 126538525259/24067258815600
P({2,3} before {7}) = P({2} before {3,7}) * P({3} before {7}) + P({3} before {2,7}) * P{{2} before {7})
When the set you want has just one number, the probability of rolling it before the set of other numbers is the number of ways to make the one number divided by the number of ways to make that number plus the others. So, for example, P({2} before {3,7}) = 1 / (2 + 6) = 1 /8.
The exact probabilities produced by the program are P(small) = P(tall) = 20049/760760 and P(all) = 126538525259/24067258815600
#! /usr/bin/env python3
from fractions import Fraction
#0 1 2 3 4 5 6 7 8 9 10 11 12
way = [0, 0, 1, 2, 3, 4, 5, 6, 5, 4, 3, 2, 1]
memo = { }
def ways(numbers):
w = 0;
for r in numbers:
w += way[r]
return w
def p(these, those):
if len(these) == 0: return 1;
if len(these) == 1:
for w in these:
return Fraction(1, 1 + Fraction(ways(those), ways(these)))
s = str(these) + str(those)
if s in memo: return memo[s]
v = Fraction(0)
full = these | those
for r in these:
only_r = frozenset([r])
full_but_r = full - only_r
these_without_r = these - only_r
v += p(only_r, full_but_r) * p(these_without_r, those)
memo[s] = v
return v
seven = frozenset([7])
small = frozenset([2, 3, 4, 5, 6])
tall = frozenset([8, 9, 10, 11, 12])
full = small | tall
print('small', p(small, seven))
print('tall ', p(tall, seven))
print('full ', p(full, seven))
July 5th, 2018 at 11:34:51 AM
permalink
Wow, hyrosen. Impressive first post. Welcome!
If the House lost every hand, they wouldn't deal the game.
July 10th, 2018 at 3:23:31 PM
permalink
Thanks. I just noticed a small error in my comment (not in the code). P({2} before {3,7}) = #2 / (#2 + #3 + #7) = 1 / (1 + 2 + 6) = 1 / 9 (not 1 / 8 as I have it).


