September 24th, 2024 at 1:32:23 AM
permalink
Can someone help me calculate the house edge on a standard 52 card deck?
If the sum of your two cards plus the dealers face up card equals any of these numbers then a payout is triggered.
3 - 100:1
4 - 50:1
5 - 30:1
30 - 7:1
29 - 3:1
28 - 2:1
If the sum of your two cards plus the dealers face up card equals any of these numbers then a payout is triggered.
3 - 100:1
4 - 50:1
5 - 30:1
30 - 7:1
29 - 3:1
28 - 2:1
September 24th, 2024 at 6:51:59 AM
permalink
Quote: justwantapCan someone help me calculate the house edge on a standard 52 card deck?
If the sum of your two cards plus the dealers face up card equals any of these numbers then a payout is triggered.
3 - 100:1
4 - 50:1
5 - 30:1
30 - 7:1
29 - 3:1
28 - 2:1
link to original post
Hi there.
I hope my combinatorial analysis isn't completely wrong:
There are 52*51*50=132600 ways to draw the first three cards out of a freshly shuffled 52 card deck.
Plausibility test:
There are 6 ways to arrange three cards. 132600/6=22100.
22100 also is the result of combin(52,3) or "52 choose 3".
Based on the probability distribution of the sums of the first three cards, as shown below, the house edge appears to be 49.12%.
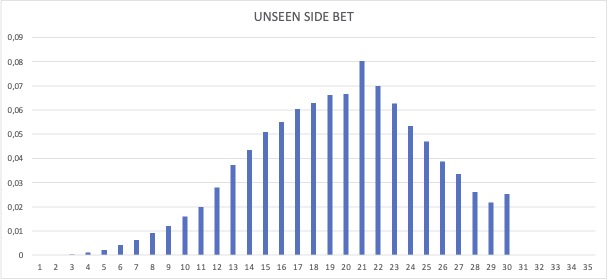
Remark: 1, 2, and 31 through 35 are included as plausibility checks only.
3 is the first regular sum of cards, but its probability is only slightly greater than zero and therefore nearly invisible.

"When it comes to probability and statistics, intuition is a bad advisor. Don't speculate. Calculate." - a math textbook author (name not recalled)
September 24th, 2024 at 7:08:10 AM
permalink
Quote: ThomasKQuote: justwantapCan someone help me calculate the house edge on a standard 52 card deck?
If the sum of your two cards plus the dealers face up card equals any of these numbers then a payout is triggered.
3 - 100:1
4 - 50:1
5 - 30:1
30 - 7:1
29 - 3:1
28 - 2:1
link to original post
Hi there.
I hope my combinatorial analysis isn't completely wrong:
There are 52*51*50=132600 ways to draw the first three cards out of a freshly shuffled 52 card deck.
Plausibility test:
There are 6 ways to arrange three cards. 132600/6=22100.
22100 also is the result of combin(52,3) or "52 choose 3".
Based on the probability distribution of the sums of the first three cards, as shown below, the house edge appears to be 49.12%.
Remark: 1, 2, and 31 through 35 are included as plausibility checks only.
3 is the first regular sum of cards, but its probability is only slightly greater than zero and therefore nearly invisible.
link to original post
I agree with your number of 49.12% (or more precisely 49.12217%.)
This assumes that the payouts are on a "to" basis (not "for.") And aces cannot count as 11.


