Basic strategy to prioritize wins

I understand that blackjack basic strategy gives the player the best ROI in the long run. How would the strategy be adjusted if I want to prioritize winning the hand instead of winning the most money? A 1 unit win is as good as a 2 unit win and a push is as bad as a loss. Obviously I wouldn't worry about doubling but I'm wondering if a strategy for the splitting decisions already exists somewhere.

This question has been asked here a few times and dismissed.

I've no idea but can point you to freebet Blackjack where the free part only pays out on a win. So this gives you a hit/stand strategy (e.g. hit 17 vs 7 8 9). I should imagine you still double where it's a clear +EV but probably not for close decisions (e.g. 10 vs 9).

You could also look for Pontoon-like games, where a tie loses, and see if there are any strategy tips there.

Quote: Wiggins

I understand that blackjack basic strategy gives the player the best ROI in the long run. How would the strategy be adjusted if I want to prioritize winning the hand instead of winning the most money? A 1 unit win is as good as a 2 unit win and a push is as bad as a loss. Obviously I wouldn't worry about doubling but I'm wondering if a strategy for the splitting decisions already exists somewhere.
link to original post

Wiggins,

Here you go! If you are dealt a pair, consult the Pair chart; otherwise, use the appropriate Hard or Soft chart.





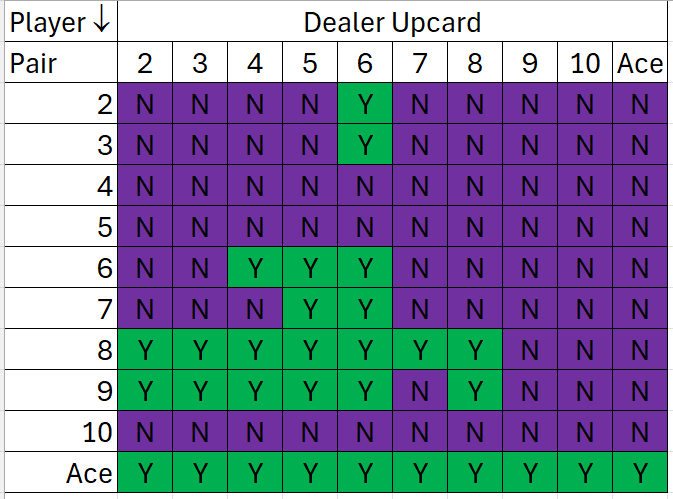
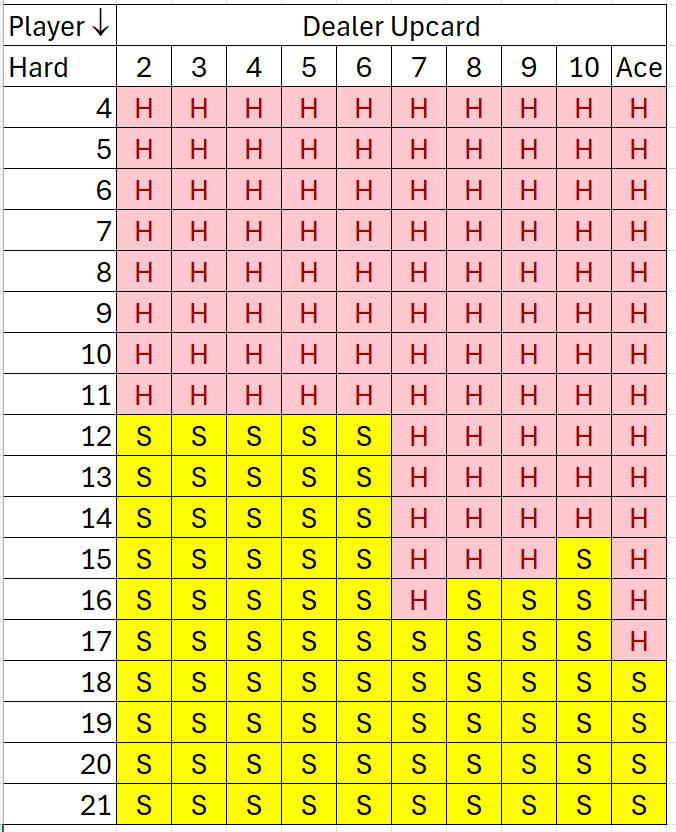
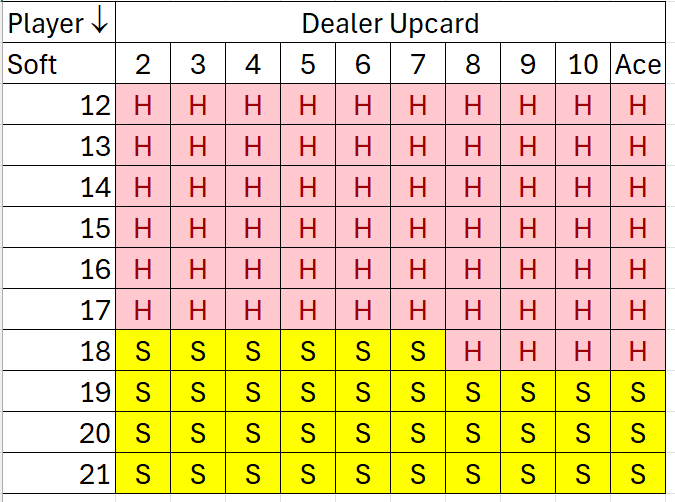
Disclaimers: These results are for INFINITE DECKS, DEALER STANDS ON S17, ONE SPLIT ONLY, and NO HITTING ON SPLIT ACES.

I obtained these results by modifying the Wizard's method of calculating Basic Strategy that he posted on YouTube:
I changed the values on the "stand" sheet by making ties lose. For example, on the stand sheet, the formula for standing on hard 17 vs. a dealer's 2 in cell B15 for the Wiz and me are these:

WIZ's: =dealer!B2-SUM(dealer!B4:B7)
MINE: =dealer!B2-SUM(dealer!B3:B7)

My version says if the dealer has 17 (in cell dealer!B3), the player loses.

The other changes are to set the EV for doubling and surrendering to -2 for all cases, so these options will never be the best option.

Hope this helps!

Dog Hand

P.S. aceside, if you previously posted this query, I'm sorry I missed it.

Great work!

If possible, could you also consider the question that was left over a few weeks ago here. Consider the same infinite deck game just like what you describe above. What are the win, loss, and tie rates of a player hand if player plays basic strategy to maximize EV.

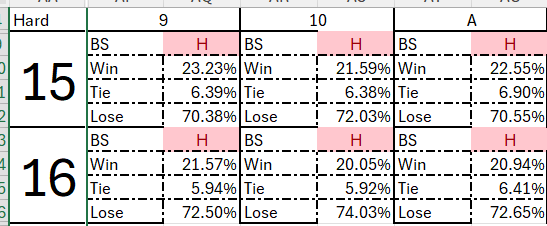
For example, for the hand of hard 16 vs T, the basic strategy is Hit. The win, loss, tie rates are 21%, 74%, and 5% respectively, if player hits.

Thanks so much for taking the time to do that. Very helpful.

Was trying to make a run at a 4 hour leaderboard on Draftkings. They typically use total dollars wagered for the standings, but this one instead awarded points for any winning wager $5 or more. Nonstop blackjack for four hours was miserable and I only took 32nd place for my troubles ($75 prize). iPhone 12 wasn't up for the challenge and laptop was no faster.

Quote: aceside

Great work!

If possible, could you also consider the question that was left over a few weeks ago here. Consider the same infinite deck game just like what you describe above. What are the win, loss, and tie rates of a player hand if player plays basic strategy to maximize EV.

For example, for the hand of hard 16 vs T, the basic strategy is Hit. The win, loss, tie rates are 21%, 74%, and 5% respectively, if player hits.
link to original post

aceside,

Here you go! These results are for infinite decks, S17, one split only, no hitting on split aces.

Pairs: for N, the W/T/L% are for Not Splitting; for Y, they're the percentages for each split hand:

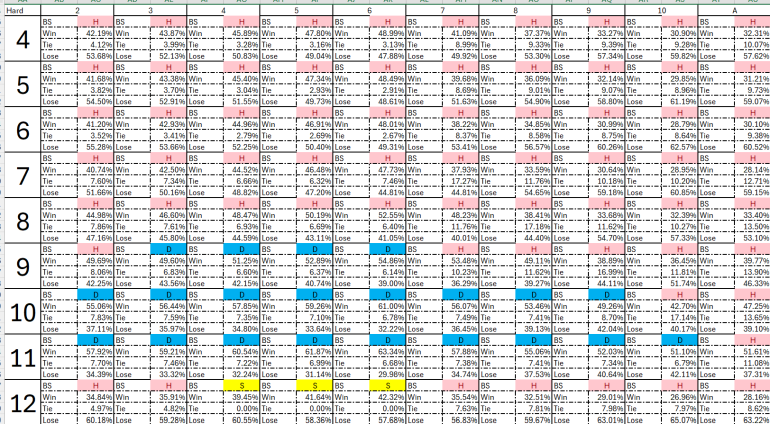
Hard with Surrender:


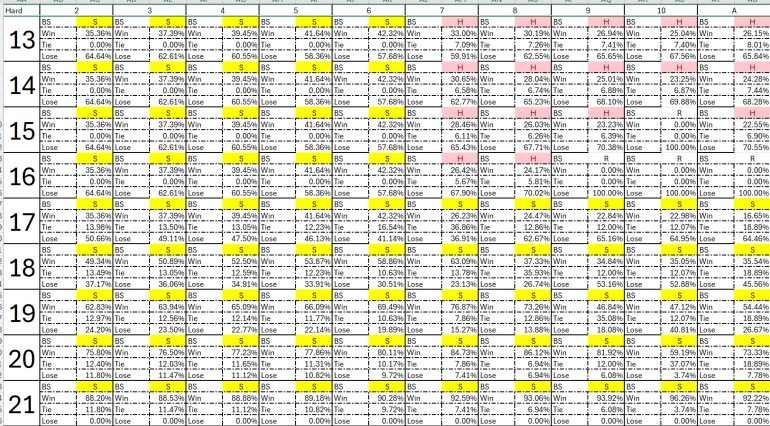
Soft with Surrender (Soft without Surrender results are the same):

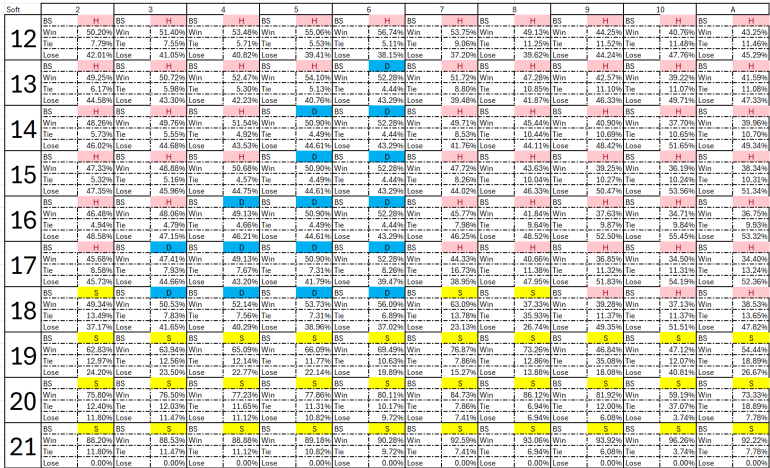
Hard without Surrender: Only changes are for 15 vs. 10 and 16 vs. 9, 10, A:


Now, what are you going to do with these numbers?

Dog Hand

This is wonderful! At least you may provide an overall calculated win/tie/loss probability for an infinite deck blackjack game. Wizard provided these numbers, 42.22%/8.48%/49.10%, but I guess they are probably from simulations on a 6-deck shoe.

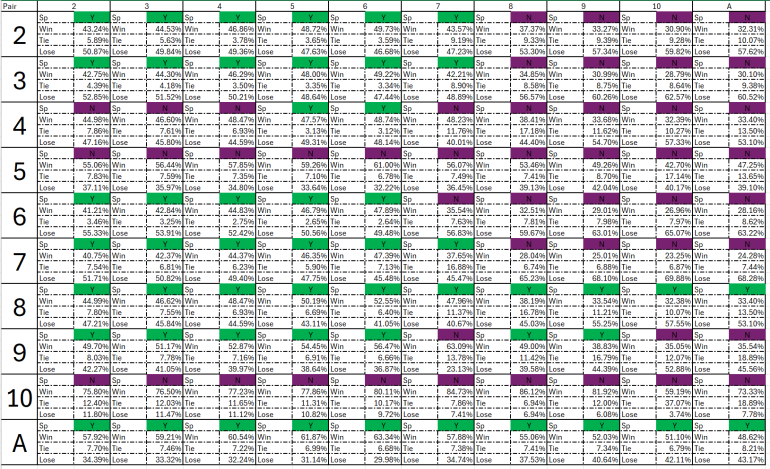
Upon more careful examination, I noticed some inconsistencies. I summarized your pair-splitting table into a graph, as shown below. The green cells indicate Split in basic strategy, whereas these green cells with a “P” indicate those Split situations where the win rate is also greater than the loss rate. These three hands, 6,6 vs. 4, 6,6 vs. 5, and 6,6 vs. 6, indicate No-Split in my table, but Split in your earlier table when a push is counted as a loss. Please double check.

I’ve thought about this issue again. For these three hands, 6,6 vs. 4, 6,6 vs. 5, and 6,6 vs. 6, the win rate of each pair-splitting is consistently less than their respective loss rate; however, basic strategy still dictates a Split decision to maximize the (positive) EV. Is this because the double-down-after-splitting option makes the average win amount greater than the average loss amount?

aceside,

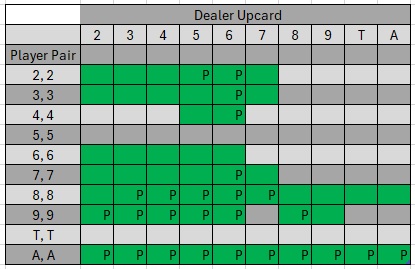
Many of the BS splits are "defensive splits", meaning the Win% is less than the Lose%. The key, though, is that NOT splitting is even worse.

For 6,6 vs. 4, splitting gives W%/T%/L% of 44.83/2.75/52.42. If we ignore DAS, the EV for each hand is 44.83 - 52.42 = -7.59%. If instead you don't split, then you stand on 12 vs. 4, which gives W%/T%/L% of 39.45/0/60.55, so the EV is 39.45 - 60.55 = -21.10%.

Splitting requires another bet, so we compare 2*(-7.59) = -15.18% to -21.10%. Since -15.18% is larger, we split.

In fact, the splitting EV is higher (less negative) than -15.18%, because we can re-split and DAS. Note that re-split is NOT included in the results I gave above in this thread.

Hope this helps!

Dog Hand

I see. First of all, for a 6-deck shoe game I often play, I know these three pair-splittings, 6,6 vs. 4, 6,6 vs. 5, and 6,6 vs. 6, are all “offensive” for an optimized positive EV.

For an infinite deck game, I still need to find out which of these are “defensive” and which are “offensive.”

For this particular purpose of maximizing the win percentage for a blackjack hand, “defensive” may mean something different, especially for a pair-splitting hand. In any case, a winning hand of 6,6 vs. 4 still means that the net gain is greater than zero.

Hi Dog, I’m still confused with this part of calculation.

For the hand 16 vs. T, your percentages, win%/tie%/loss% = 20.05/5.92/74.03; therefore,
EV = 20.05%-74.04% = -53.98%,
Which agrees with Wizard’s calculation number of -53.983%.

For the hand 6,6 vs. 4, your percentages, win%/tie%/loss% = 48.83/2.75/52.42; therefore,
EV = 48.83%-52.42% = -7.59%,
Which does NOT agree with Wizard’s calculation number of -4.956%.

For the hand 6,6 vs. 5, your percentages, win%/tie%/loss% = 46.79/2.65/50.56; therefore,
EV = 46.79%-50.56% = -3.77%,
Which does NOT agree with Wizard’s calculation number of +4.399%.

How to calculate the EV from the win%/tie%/loss%? Also, my intuition tells me that the tie percentages for these two hands, 6,6 vs. 4 and 6,6 vs. 5, should be a lot higher than your calculation numbers because it’s more likely to have a one-win-one-loss result for two split hands. Please help.

Quote: aceside

Hi Dog, I’m still confused with this part of calculation.

For the hand 16 vs. T, your percentages, win%/tie%/loss% = 20.05/5.92/74.03; therefore,
EV = 20.05%-74.04% = -53.98%,
Which agrees with Wizard’s calculation number of -53.983%.

For the hand 6,6 vs. 4, your percentages, win%/tie%/loss% = 48.83/2.75/52.42; therefore,
EV = 48.83%-52.42% = -7.59%,
Which does NOT agree with Wizard’s calculation number of -4.956%. Kolp

For the hand 6,6 vs. 5, your percentages, win%/tie%/loss% = 46.79/2.65/50.56; therefore,
EV = 46.79%-50.56% = -3.77%,
Which does NOT agree with Wizard’s calculation number of +4.399%.

How to calculate the EV from the win%/tie%/loss%? Also, my intuition tells me that the tie percentages for these two hands, 6,6 vs. 4 and 6,6 vs. 5, should be a lot higher than your calculation numbers because it’s more likely to have a one-win-one-loss result for two split hands. Please help.
link to original post

aceside,

For 16 vs. X, you CAN calculate EV as W% - L%, because if you win, you'll win only 1 unit since you would not DD.

For Split hands, your average win PER HAND will be more than 1 unit, because of DAS. For example, when you split 6,6 vs. 5, you will DD if the next card is 3, 4, 5, or A.

Furthermore, as I mentioned above in this thread, the numbers I showed were for a game with no resplitting, so if you get a 6 after splitting 6,6 vs. 5, you're now stuck playing a -EV 12 vs. 5, whereas in a real game you'd probably have the option to re-split.

Finally, as I also mentioned above in this thread, on the Pairs table, if BS is Split, the W/T/L percentages are for EACH HAND of the split. For 6,6 vs. 5, the W% is 46.79, so the chance to win BOTH hands of the split is (46.79%)² = 21.89%. The L% is 50.56%, so the chance to lose BOTH hands of the split is (50.56%)² = 25.56%. The remaining 52.54% of the time you'll either W+T, W+L, T+T, or T+L. However, even W+L doesn't guarantee an overall push, because of DD hands. Also, your actual game will probably permit re-splits which further complicates the calculations.

Hope this helps!

Dog Hand

P.S. Do you see how why we usually just look at EV rather than the W/T/L %'s?

I start to understand you. If double-down-after-splitting (DAS) is not allowed, it seems to me that we should be able to calculate out an overall win/tie/loss percentage for the infinite deck blackjack game you described.

Another question. In the pair-splitting strategy table you posted earlier when the win percentage is optimized and a push is counted as a loss, you listed the decision for the hand 6,6 vs. 4 as Split. So, how did you calculate the win percentage for this hand? Did you consider the net gain for both split hands together, or just one of them?

Thank you for your patience!

aceside,

If noDAS and no re-splitting, we could calculate the overall EV... but that would be a terrible game. Remember that the results I gave are for No Dealer BJ: thus, they would change for upcards of X and A. The Wiz posted another YouTube video showing how to calculate the overall EV including DAS but no re-splits.

For 6,6 vs. 4 with Ties lose, the EV for standing on 12 vs. 4 is -21.1%, so -0.211 units. The EV for splitting is -10.1% for each hand, so -0.202 units. Thus, splitting is the less objectional play. Also, since the best EV is negative, this is an example of a defensive split.

Hope this helps!

Dog Hand

I see what you calculated for the hand of 6,6 vs. 4; however, I believe what the OP asked for is the maximized win percentage for this hand. I still need to look more into this part. Thank you!

Quote: DogHand

Finally, as I also mentioned above in this thread, on the Pairs table, if BS is Split, the W/T/L percentages are for EACH HAND of the split. For 6,6 vs. 5, the W% is 46.79, so the chance to win BOTH hands of the split is (46.79%)² = 21.89%. The L% is 50.56%, so the chance to lose BOTH hands of the split is (50.56%)² = 25.56%. The remaining 52.54% of the time you'll either W+T, W+L, T+T, or T+L. However, even W+L doesn't guarantee an overall push, because of DD hands. Also, your actual game will probably permit re-splits which further complicates the calculations.

I’ve figured out how to calculate the EV from the Win/Tie/Loss percentages. Let me use the hand of 6,6 vs. 5 as an example to demonstrate it. After splitting this pair 6,6, player may receive a 2, 6, 7, 8, 9, T card for hitting or standing, or a 3, 4, 5, A card for doubling. Below are the respective W%/T%/L% numbers:

If player hits or stands, 42.59/0.07/56.67;
If player doubles, 56.23/6.94/36.83;
The overall average, 46.79/2.65/50.56.

With these numbers,
EV = 2 [(42.59-56.67) 9/13 +2 (56.23%-36.83%) 4/13] = 4.39%,
which agrees with Wizard’s calculation number.

Also, I found something interesting. If we consider the combined win percentage of the two split hands as a whole, we should not split any pair hand, except these two, 8,8, vs. 7 and 8,8, vs. 8. Please check.

Quote: aceside

<snip>Also, I found something interesting. If we consider the combined win percentage of the two split hands as a whole, we should not split any pair hand, except these two, 8,8, vs. 7 and 8,8, vs. 8. Please check.
link to original post

aceside,

I don't follow your reasoning.

Part of the problem is perhaps a miscommunication about the objective. What precisely are you trying to achieve?

Dog Hand

My objectives are two-fold.

1. Find the overall win/tie/loss percentages of a blackjack hand in basic strategy.
2. Find the strategy decision that gives the maximum win percentage of a hand.

To avoid complications from DAS, let me use this hand, A,A vs. 5, as an example to demonstrate.

If player splits, for each split hand, W%/T%/L% = 61.87/6.99/31.14; therefore, the overall two-hand combined W%/T%/L% = 46.92/39.02/14.05.
If players hits, W%/T%/L% = 55.06/5.53/39.41.

Therefore, player should hit to gain a higher win percentage of 55.06% for this hand of A,A vs. 5. I hope this makes sense.

Quote: aceside

My objectives are two-fold.

1. Find the overall win/tie/loss percentages of a blackjack hand in basic strategy.
2. Find the strategy decision that gives the maximum win percentage of a hand.

To avoid complications from DAS, let me use this hand, A,A vs. 5, as an example to demonstrate.

If player splits, for each split hand, W%/T%/L% = 61.87/6.99/31.14; therefore, the overall two-hand combined W%/T%/L% = 46.92/39.02/14.05.
If players hits, W%/T%/L% = 55.06/5.53/39.41.

Therefore, player should hit to gain a higher win percentage of 55.06% for this hand of A,A vs. 5. I hope this makes sense.
link to original post

aceside,

Would you demonstrate how you got from "W%/T%/L% = 61.87/6.99/31.14" to the "overall two-hand combined W%/T%/L% = 46.92/39.02/14.05"?

Dog Hand

(w + t + l)^2 = (w^2 + 2 w t) + (t^2 + 2 w l) + (l^2 + 2 l t) = W + T + L