Least Costly BJ Mistakes

Hello everyone,

Is there a list of least costly blackjack basic strategy mistakes arranged by Δ EV?

Thanks

What’s your purpose of asking this question? Does the answer help you to become a better gambler? Apparently the least costly decision is 16 vs. 10.

What you are referring to is something that I and other analysts refer to as "close-call" decisions. They are interesting because knowledge of other cards that no long remain in the deck can flip the basic strategy decision.

For a no surrender, S17 blackjack game, I believe these are the closest decisions. In general this list trends from closest decision on top of the list to least close on the bottom.

16 vs T, No Dealer BJ:
12 vs 4:
13 vs 2:
A7 vs 2:
A6 vs 2:
33 vs 2:
A4 vs 4:
A3 vs 5:
A8 vs 6:
77 vs 8:
33 vs 8:
9 vs 2:

I like the question and answer, regardless of what prompted it.

Not to troll serious gamblers, but I've never been a fan of anything -EV. So if I sit down to play 21 for fun knowing I expect to lose, the last thing I want to do is play by a rote strategy where I make no decisions at all. Knowing there are some decisions that aren't really bad helps make the game fun.

The analogy in craps is tossing out an occasional 6/8 place bet rather than only playing the line and max odds. Whereas, a hard 6 or 8 would be a more costly "fun" play.

If I expect my bankroll to last 3 hours with basic strategy, but by actually making some decisions or playing some minor hunches I can have 2 hrs and 50 minutes of a more fun activity, so be it. If someone is card counting or trying for a razor thin edge, that's another story.

https://wizardofodds.com/games/blackjack/expected-values/

These are Mike's raw expected value charts for different rule sets. You should be able to copy and paste the tables to a spreadsheet. Then, you can create formulas for differences between different actions in added columns. You can use conditional formatting to highlight the smallest EV differences. Or, you can sort the delta EVs to find the closest decisions.

You could also use Gordon's table to just search Mike's tables to find the deltas. Then you will see that 9 vs 2 is not H vs S, but H vs D.

Here are the top least costly mistakes in blackjack, assuming six decks, dealer hits soft 17, double after split allowed, re-split to four hands.

PLAYER	DEALER	Best play	Second best play	Difference
9,7	10	H	S	0.001417
7,A	2	D	S	0.003152
2,A	5	D	H	0.003412
4,A	4	D	H	0.004521
6,A	2	H	D	0.004608
10,2	4	S	H	0.004758
7,2	2	H	D	0.006043
10,6	10	H	S	0.006278
5,4	2	H	D	0.007747
6,3	2	H	D	0.007953

These are all 2-card player hands. As I discussed with Mental a few days ago here, there are still some multiple-card player hands too, such as

466 vs. 10,
367 vs. 10,
268 vs 10,
A69 vs. 10.

It’s possible that some of these hands may have an even lower hit/stand EV difference.

If you want looser play to "make sense", then what my thinking has been is to choose those that increase the variance. I won't go into why increasing variance can be good in a -EV game.

I think we can assume that doubling and splitting increase the variance, I think that can be shown. So, for those decisions on whether to double or split, or not, then those that cost very little have appeal. When I play BJ, I'll probably only sit through one or more shoes, and I'd rather have more dynamic up and down swings. YMMV

here are some you can go with that I've found. The cost, meaning increase in EV, is per $10 bet. Experience has shown few of these will come up in any given shoe

*soft 13, doubling vs dealer 4, cost of 36 cents
*soft 14, doubling vs 4, cost of 15 cents
*soft 19, doubling vs 5,  29 cents
*doubling with 10 vs 10, 33 cents
*doubling with 9 vs 2,   9 cents
*doubling with 8 vs 6 ,  25 cents
*splitting, das allowed, 4,4 vs 4, 40 cents 
*splitting, das allowed, 6,6 vs 7,  37 cents

these as well, cost of which I have lost

*double soft 15 versus dealer 3
*double soft 16 versus dealer 3 
*double soft 17 versus dealer 2 
*split player pair 2,2 vs dealer 8 
*split player pair 3,3 vs dealer 8  
*split player pair 7,7 vs dealer 8 
*split 9,9 vs dealer 7

If I play 400 hands and I'm up 6%, trying out these shortcuts could cut my profit in half. But you say it can increase my variance so give it a try. I'll save it for later.

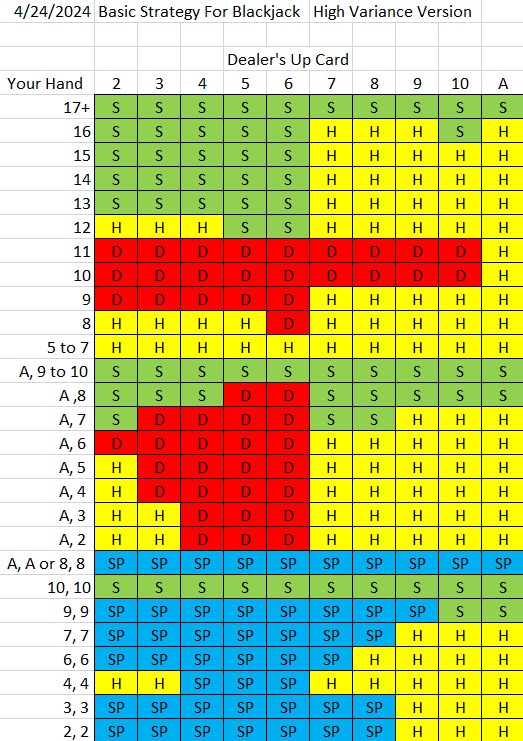
I wrote up a Basic Strategy chart that may reflect the previous posts. I used "4" for the column width.
Apparently, I still think it's yesterday.

Quote: ChumpChange

If I play 400 hands and I'm up 6%, trying out these shortcuts could cut my profit in half. But you say it can increase my variance so give it a try. I'll save it for later.
link to original post

if you're playing BJ +EV [card counting] you earned the 'up 6%' ... that person shouldn't want to increase variance, which would be more likely to wipe it out than increase the gain

Me? Variance is my only chance to come out a winner, I'm not counting cards. Yet, I want to follow BS to limit my losses, only doing things to increase variance that don't cost me much

This question has been asked somewhere online, but the answer is still not clear to me. Let me move it to here.

Consider a 6-deck stand-17 shoe game with a cut card at a 4.5/6 deck-depth. If player plays perfect strategy every hand, what is the player’s edge?

Quote: aceside

This question has been asked somewhere online, but the answer is still not clear to me. Let me move it to here.

Consider a 6-deck stand-17 shoe game with a cut card at a 4.5/6 deck-depth. If player plays perfect strategy every hand, what is the player’s edge?
link to original post

You mean computer perfect counting? What’s the assumption on bet sizing and ability to Wong in and out?

Yes, we assume flat bet all the way and computer perfect play too.

Quote: aceside

Yes, we assume flat bet all the way and computer perfect play too.
link to original post

Flat betting means -EV and the HE is what it is, all rules considered

in other words basic strategy gives no edge [perfect play is assumed when you see an HE figured], and card counting gives no edge flatbetting

Quote: odiousgambit

Quote: aceside

Yes, we assume flat bet all the way and computer perfect play too.
link to original post

Flat betting means -EV and the HE is what it is, all rules considered

in other words basic strategy gives no edge [perfect play is assumed when you see an HE figured], and card counting gives no edge flatbetting
link to original post

That’s not quite right. He’s asking what the edge would be if you deviate from BS when warranted based on computer perfect play.

Quote: gordonm888

What you are referring to is something that I and other analysts refer to as "close-call" decisions. They are interesting because knowledge of other cards that no long remain in the deck can flip the basic strategy decision.

For a no surrender, S17 blackjack game, I believe these are the closest decisions. In general this list trends from closest decision on top of the list to least close on the bottom.

16 vs T, No Dealer BJ:
12 vs 4:
13 vs 2:
A7 vs 2:
A6 vs 2:
33 vs 2:
A4 vs 4:
A3 vs 5:
A8 vs 6:
77 vs 8:
33 vs 8:
9 vs 2:
link to original post

That's a cool list! In blackjack, especially when cards are considered, decisions like 16 vs. 10 can minimize losses. It's important to adapt your strategy to your deck situation for the best results.