Counter-phobia at a casino gives a huge hidden advantage!

I heard of a casino (I forgot exactly where, if the story is indeed real) in which they're so paranoid about card counters with their pitch games that they don't reveal face-down cards unless it's necessary. That means if everyone had a blackjack and/or busted the dealer doesn't show the hole card, and if the dealer busts double-down hands are never exposed. The latter gives a major advantage for the player: Since they didn't consider that players may double a stiff hand, this makes it that if you double (or double for less) a double bust is a win for the player! How much of an advantage does this give the player? What would the basic strategy be?

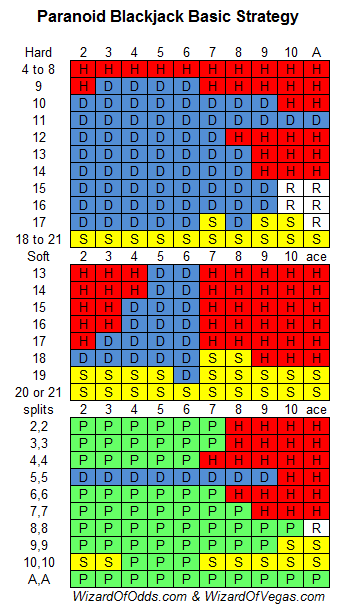
I got an estimate of the strategy on hands of 12-16 using the Wizard's infinte deck table of EVs (since this is a pitch game there may be a few differences). Since in an infinite deck doubling a 12-16 has the same EV as a soft hand in this range (since a double bust has the same effect when doubling as ending up with a total of less than 16, in that you win precisely when the dealer busts and lose otherwise), I compared those EVs to the standard hit/stand ones and came up with the following for player hands of 12-16, broken down by whether or not doubling for less is allowed.

If doubling for less is allowed:
Double for full if the dealer shows a 4, 5, or 6; double for less with any other upcard.

If doubling for less is not allowed:
Double except with a 12 vs. 8, 12-14 vs. 9, 12-15 vs. 10, or any of these hands vs. A.

Pairs of 6s: Don't split.

Pairs of 7s: Split only with dealer 5, 6, or 7.

Pairs of 8s: Split unless the dealer shows a 9, 10, or A and doubling for less is allowed.

Note that the EV of hitting goes down as you go up from 12 to 16, so that's why some of these hands go from hit to double as you go up.

When it says to double when doing so for less is allowed, but not when a full double would be indicated if not allowed, whether or not you actually should depends on the ratio of the minimum double amount allowed in relation to your original bet.

Since there was no way for me to do a quick analysis with hands of 17+ (since comparing it to soft doubling won't work in that case), I couldn't come up with anything for those hands.

Are you SURE about those rules?

I see no reason why you indicate that only a double down hand might be paid without checking after a dealer bust. Why wouldn't a hand with a single hit be similar? For that matter, why would ANY hand with more than two cards be believed to not be busted?

Casino paranoia is understandable, but to allow a player's busted hand to be paid is out of the question.

I'd believe that such a paranoid casino would use rules like these:

1 - Request that no cards are revealed.
2 - Do not reveal a blackjack until after the dealer plays his hand.
3 - If a player busts, simply admit it and fold without showing cards - with warnings and even being barred from play for failure to fold a busted hand.
4 - If a player does not hit, and the dealer busts, pay the player without exposing the cards.
5 - If a player takes a hit, do not expose it until after the dealer plays his hand.

If the dealer does not bust, you have to check the players' cards, so I do not see why they wouldn't check them even if the dealer does bust.

In most sane cases, you can't bust after a double, so they won't bother to turn the card over if the dealer busted.
I am sure if you doubled a hard sixteen, you are getting your card face up though :)

Quote: Kellynbnf

I heard of a casino (I forgot exactly where, if the story is indeed real) in which they're so paranoid about card counters with their pitch games that they don't reveal face-down cards unless it's necessary. That means if everyone had a blackjack and/or busted the dealer doesn't show the hole card, and if the dealer busts double-down hands are never exposed.

Except "unless it's necessary" means you'd need to reveal any potentially-busted player hands to comply with the actual rules of the game. A fundamental premise of blackjack is that if both the player and dealer bust their hands, the player loses.

Quote: Kellynbnf

I heard of a casino (I forgot exactly where, if the story is indeed real) in which they're so paranoid about card counters with their pitch games that they don't reveal face-down cards unless it's necessary. That means if everyone had a blackjack and/or busted the dealer doesn't show the hole card, and if the dealer busts double-down hands are never exposed. The latter gives a major advantage for the player: Since they didn't consider that players may double a stiff hand, this makes it that if you double (or double for less) a double bust is a win for the player! How much of an advantage does this give the player? What would the basic strategy be?

I got an estimate of the strategy on hands of 12-16 using the Wizard's infinte deck table of EVs (since this is a pitch game there may be a few differences). Since in an infinite deck doubling a 12-16 has the same EV as a soft hand in this range (since a double bust has the same effect when doubling as ending up with a total of less than 16, in that you win precisely when the dealer busts and lose otherwise), I compared those EVs to the standard hit/stand ones and came up with the following for player hands of 12-16, broken down by whether or not doubling for less is allowed....

The dealer will see that you often double on stiff hands and will start checking your double-down card when he busts. Nevertheless, I agree that you would double stiff hands vs 4, 5, or 6. I would double for less all stiffs vs all other cards, depending on the relative size of the first bet and the double-for-less bet. The same would apply to 17 except that I would stand with 17 vs 7.

I used an infinite-deck analysis, too, and assumed that the dealer hits soft 17 and does not allow doubling after splitting. I also assumed that the dealer will check your non-doubled hands for busts when he busts. Here is my splitting strategy: split A's vs all, split 2's and 3's vs 4-7, split 8's vs 3-8, and split 9's vs 2-6 and 8-9. Allowing one split, I get a player advantage of 8%, again depending on the relative sizes of the first bet and the double-for-less bet.

Quote: Kellynbnf

I heard of a casino (I forgot exactly where, if the story is indeed real) in which they're so paranoid about card counters with their pitch games that they don't reveal face-down cards unless it's necessary. ...

I'm not sure about this sort of thing. Its pretty much the same as that Bellagio robbery: let the chips go and avoid gunplay in a crowded casino is a good policy, but it does cost them paperwork, publicity and new chips.

Sort of the same concept with paranoia and card-counters. If you have the Dealers, Floors and Pit Bosses all focusing on possible cardcounters and you adopt special procedures to defeat card-counters, the casino is probably robbing its own pocket of a great deal just to be sure some anonymous and perhaps non-existent card-counter doesn't rob their pocket of a few pennies.

Okay, I am getting a very unusual basic strategy for what I'm calling "paranoid rules."



Assuming six decks, dealer hits a soft 17, surrender, re-splitting ace, and double after a split I show a player advantage of 4.9%.

Can anyone confirm this? Miplet? ME?

Quote: Wizard

Okay, I am getting a very unusual basic strategy for what I'm calling "paranoid rules." ...

Wizard, since posters in this thread have speculated on different interpretations of the rules, can you clarify what "paranoid rules" you are considering? In particular, do you assume that if the dealer busts, then the players' hands aren't examined for busts?

Quote: Doc

Wizard, since posters in this thread have speculated on different interpretations of the rules, can you clarify what "paranoid rules" you are considering? In particular, do you assume that if the dealer busts, then the players' hands aren't examined for busts?

Yes, but only double down bets.

Quote: Wizard

...Assuming six decks, dealer hits a soft 17, surrender, re-splitting ace, and double after a split I show a player advantage of 4.9%. ...

Can anyone confirm this? Miplet? ME?

Using the infinite-deck model, I'm very close to your 4.9% value with 4.83%. I agree with your strategy details. My previous value of 8% allowed the player to double for less.

Quote: ChesterDog

Using the infinite-deck model, I'm very close to your 4.9% value with 4.83%. I agree with your strategy details. My previous value of 8% allowed the player to double for less.

Thanks. If I assumed infinite decks I would be at 5.0%. I subtracted 0.1% for a six-deck game. Good thinking about doubling for less. Here is my strategy allowing that. I assume the player can double for less for an insignificantly small amount, for example a penny after a $100 bet. Here is that strategy.



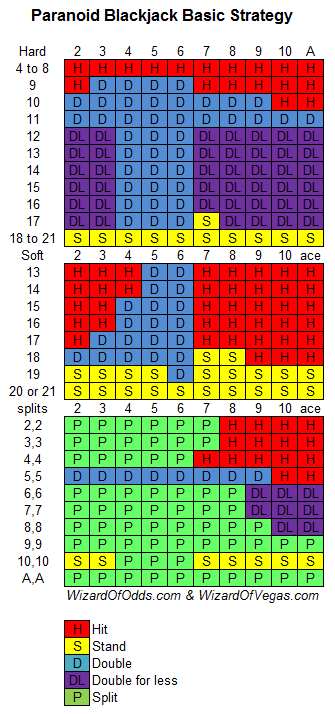
My infinite-deck house edge is 9.35%, which is too far from your figure for comfort. Does my strategy give any clues to where our point of departure might be?

Quote: Wizard

...My infinite-deck house edge is 9.35%, which is too far from your figure for comfort. Does my strategy give any clues to where our point of departure might be?

My 8% figure was based on split only once and no double after split. When I change to split to four hands, resplit aces, and double after split allowed, I get 9.18% allowing double for less (~1 penny.) All the details of our strategies agree.

Quote: Kellynbnf

I heard of a casino (I forgot exactly where, if the story is indeed real).

So far nobody has piped up and said they know of such a casino. Maybe they should keep it to themselves! And I think you'd have the "kill the golden goose" problem, too, of getting casino heat in such a paranoid place, getting yourself booted somehow, or getting your unseen busts exposed out of suspicion at the very least. How best to handle that?

I would think that if such a place with those rules existed, they would of course be checking your double card if you doubled on 12 or more. If they're so worried about counters, I think they would be just as worried about checking the card if you could bust. They may allow double on 9 - 11, for example.

Quote: ChesterDog

My 8% figure was based on split only once and no double after split. When I change to split to four hands, resplit aces, and double after split allowed, I get 9.18% allowing double for less (~1 penny.) All the details of our strategies agree.

Thanks for the confirmation! :-)

deleted

Hypothetically, if you knew of a game with a PA of 5-10%, how much would you even play? Fully kelly would be excessive. It seems like its almost a prisoners dilemna, do you play as much as possible because you know everyone else will try to play as much as possible before the rules are rescinded, or do you play a lesser amount in the hopes that everyone collectively realizes that they wouldn't want to "kill the golden goose?"

Quote: Lote

Hypothetically, if you knew of a game with a PA of 5-10%, how much would you even play? Fully kelly would be excessive. It seems like its almost a prisoners dilemna, do you play as much as possible because you know everyone else will try to play as much as possible before the rules are rescinded, or do you play a lesser amount in the hopes that everyone collectively realizes that they wouldn't want to "kill the golden goose?"

Assuming the rules even exist as originally mentioned, I think the casino would catch on soon enough one way or the other. Play her for all she's got, baby!

I would think if you doubled on anything that was POSSIBLE to bust (hard 12+) the dealer would check your double card on the way back through (paying the winning hands)

I don't understand doubling for less in this game. You can take another card without doubling; why is doubling for a penny better EV than hitting?

EDIT: Never mind; disregard; I'm a moron, etc.

Though charts that say "double for as little as possible" leave a small hole. Ideally you double for an amount so insignificant that really you're just taking a card face down for free, right? What would be neat to see is the critical fractions for those doubles; that is to say, the percentage increase required for the double where the EV of doubling is equal to the EV of the best non-doubling decision. If you saw a purple "0.25" in the cell, for example, you'd double for less if you could put up a quarter of your original bet or less; otherwise you'd take the action in the you-can't-double-for-less chart. (Alternatively, show the reciprocal of this fraction. This requires simpler math at the table since typically the double amount is something like a dollar. If you see a purple "20", double if your bet is $20 or more.)

Not that such a chart would ever be useful, of course, since this game probably doesn't exist :-P

Quote: foxfan20

Though charts that say "double for as little as possible" leave a small hole. Ideally you double for an amount so insignificant that really you're just taking a card face down for free, right? What would be neat to see is the critical fractions for those doubles; that is to say, the percentage increase required for the double where the EV of doubling is equal to the EV of the best non-doubling decision. If you saw a purple "0.25" in the cell, for example, you'd double for less if you could put up a quarter of your original bet or less; otherwise you'd take the action in the you-can't-double-for-less chart. (Alternatively, show the reciprocal of this fraction. This requires simpler math at the table since typically the double amount is something like a dollar. If you see a purple "20", double if your bet is $20 or more.)

Not that such a chart would ever be useful, of course, since this game probably doesn't exist :-P

Another chart your idea would be useful on (and I do know of real casinos where this would be applicable) is the one for the strategy when you are allowed to double, but not hit, after splitting aces (for the cases that a full double is not appropriate but a double-for-less would be if low enough in relation to your original bet).

That one's actually really simple. There's a thread on this forum somewhere where I posted my findings... lemme see if I can't dig it up for you.