Predicting push-22 at Free Bet BJ

I've had some good success counting Aces and 5s at Free Bet BJ even though it's a continuous shuffling machine (3:2, stand soft 17, surrender anything, split 4 times). I flat bet 3 units until the count is +2, at which point I start betting 7 units until it falls below +2.

I have a theory based on anecdotal evidence that when the count get lower than -2, a push 22 is about to happen. I start betting one unit on the 22 side bet (which pays 7x, 20x or 50x if the dealer gets 22, depending on color) and keep adding one unit whenever the count gets when lower. I've had a few instances of a 50x payout on a $25 bet and almost never got a 22 when the count was high.

Is this dumb luck, or are the odds of a push 22 truly better when a large number of Aces and a low number of 5s have been pulled in the last few rounds?

Thanks

Quote: jdmartin

even though it's a continuous shuffling machine
I have a theory based on anecdotal evidence that when the count get lower than -2,
link to original post

might be dumb luck i dont think counting works on continuous shuffle

Thanks! Assuming I can find a table where it's not a continuous shuffling machine, could the Aces count help me predict the push-22?

Quote: jdmartin

Thanks! Assuming I can find a table where it's not a continuous shuffling machine, could the Aces count help me predict the push-22?
link to original post

just an fyi i dont really know too much about counting but i was always under the impression that it was dependent on deck penetration

i have heard people talking about counting with a CSM but i never got into the conversation if it was true or not

I was curious about this problem so I decided to do an analysis using Python (pandas, Jupyter, etc.).

It's not complete yet so don't use this to gamble your own money, but I did get interesting results. I implemented the strategy outlined by the Wizard for Free Bet, but only the real money part, with no bankroll limit. Basically I just wanted to see what's the status of aces vs fives whenever the dealer hits 22.

Parameters:
- 8 decks, moving to new deck after 85%
- reset counts after 8 decks
- 2 players using the strategy described above
- dealer hit soft 17

I ran 1,000,000 rounds. Whenever the dealer got 22, the count was pushed to an array. At the end of the million rounds, the array was analyzed in pandas. And I ran this whole analysis 100,000 times to make sure there's no weird state leftover.

I got consistent results out of this half-baked simulator: about 55% of push-22 happened when the count was 0, about 30% when the count was either 1 or -1. As one would suspect it's an almost normal distribution.

This may appear obvious in retrospect since the further from zero the count gets, the more likely either side is going to win. Or it could be statistical white noise and I'm basically reading tea leaves.

In the coming days I will make a new iteration of this simulator, taking into account the entire Wizard strategy and a number of scenarios (single player, one or many players not following the correct play, etc). I am recording my progress on video and I'll share the YouTube url when I'm done.

I'm not really a math person so I'll have a friend review my conclusions as well. I don't plan on sharing the python code directly because I don't want to support it but it will be on display on the video (screen cast).

Again this could be entirely garbage but I'm confident enough that from now on I'm going to gamble a dollar on push-22 when the count is 0.

If I have any success with this or if it's fun enough, I'll tackle other side bet scenarios in various table games, at the risk of being shamed by the Wizard. I understand the house edge can get ridiculous (ex; king's bounty is like 25%) but if I can identify situations where the side bet is slightly less ridiculous I'll have a way to get my fix of high-volatility gambling while not feeling like a complete fool.

To be continued!

If you're a programmer this should be simple; find the effect of removal on each card. I.E. Remove all of the 9's, then run the game with perfect basic strategy and rules and see how many 22's happen after 1,000,000 shoes. Then do the same for every other number, and for a complete deck to compare the changes to find the EoR. Then you'll find the cards that correspond the most with the outcome you're looking for and you can create a specialized count for the push 22 on it's own. Then program your count and find at which + count it becomes positive to place a wager (might be too high to consider real... or never).

My instinct is that you will not have a winning system here, but who knows, could squeeze out an edge. Also, for your original question... if I understand it correctly then you're both just trying to play the hand the best you can, even though you're in charge of different hand signals to the dealer, correct? If that's the case the fact that there's 2 of you means absolutely nothing to the math of the game, past as someone mentioned if your "teammate" didn't want to double for the full amount and you did... but that's you just scooping up his lost EV, not actually making +EV from the deck/game/casino.

Lastly, CSM's are countable, when the dealer doesn't immediately put the cards back in the tray. Tho even then there's like a 15 card buffer before they get mixed back in, but if you're playing with more than 4 decks (and even then) your count frequencies are just god awful. It's the same as playing a 6D shoe and someone putting the cut card 15 cards in, then shuffling every time they hit the 16th card. Basically renders counting useless, so I wouldn't trust any short term results from that game and would be very willing to bet it's -EV even with what little counting you can do. You have to find a lazy dealer that let's 2 or 3 decks go, at least. Then you have to blast a massive spread and fade insane variance (kinda like playing online live blackjack).

Good luck to you on your adventure!

Quote: Romes

If you're a programmer this should be simple; find the effect of removal on each card. I.E. Remove all of the 9's, then run the game with perfect basic strategy and rules and see how many 22's happen after 1,000,000 shoes. Then do the same for every other number, and for a complete deck to compare the changes to find the EoR. Then you'll find the cards that correspond the most with the outcome you're looking for and you can create a specialized count for the push 22 on it's own. Then program your count and find at which + count it becomes positive to place a wager (might be too high to consider real... or never).

My instinct is that you will not have a winning system here, but who knows, could squeeze out an edge. Also, for your original question... if I understand it correctly then you're both just trying to play the hand the best you can, even though you're in charge of different hand signals to the dealer, correct? If that's the case the fact that there's 2 of you means absolutely nothing to the math of the game, past as someone mentioned if your "teammate" didn't want to double for the full amount and you did... but that's you just scooping up his lost EV, not actually making +EV from the deck/game/casino.

Lastly, CSM's are countable, when the dealer doesn't immediately put the cards back in the tray. Tho even then there's like a 15 card buffer before they get mixed back in, but if you're playing with more than 4 decks (and even then) your count frequencies are just god awful. It's the same as playing a 6D shoe and someone putting the cut card 15 cards in, then shuffling every time they hit the 16th card. Basically renders counting useless, so I wouldn't trust any short term results from that game and would be very willing to bet it's -EV even with what little counting you can do. You have to find a lazy dealer that let's 2 or 3 decks go, at least. Then you have to blast a massive spread and fade insane variance (kinda like playing online live blackjack).

Good luck to you on your adventure!
link to original post

Over my head.

Hi Romes.

Quote: jdmartin

I was curious about this problem so I decided to do an analysis using Python (pandas, Jupyter, etc.).

It's not complete yet so don't use this to gamble your own money, but I did get interesting results. I implemented the strategy outlined by the Wizard for Free Bet, but only the real money part, with no bankroll limit. Basically I just wanted to see what's the status of aces vs fives whenever the dealer hits 22.

Parameters:
- 8 decks, moving to new deck after 85%
- reset counts after 8 decks
- 2 players using the strategy described above
- dealer hit soft 17

I ran 1,000,000 rounds. Whenever the dealer got 22, the count was pushed to an array. At the end of the million rounds, the array was analyzed in pandas. And I ran this whole analysis 100,000 times to make sure there's no weird state leftover.

I got consistent results out of this half-baked simulator: about 55% of push-22 happened when the count was 0, about 30% when the count was either 1 or -1. As one would suspect it's an almost normal distribution.

This may appear obvious in retrospect since the further from zero the count gets, the more likely either side is going to win. Or it could be statistical white noise and I'm basically reading tea leaves.

In the coming days I will make a new iteration of this simulator, taking into account the entire Wizard strategy and a number of scenarios (single player, one or many players not following the correct play, etc). I am recording my progress on video and I'll share the YouTube url when I'm done.

I'm not really a math person so I'll have a friend review my conclusions as well. I don't plan on sharing the python code directly because I don't want to support it but it will be on display on the video (screen cast).

Again this could be entirely garbage but I'm confident enough that from now on I'm going to gamble a dollar on push-22 when the count is 0.

If I have any success with this or if it's fun enough, I'll tackle other side bet scenarios in various table games, at the risk of being shamed by the Wizard. I understand the house edge can get ridiculous (ex; king's bounty is like 25%) but if I can identify situations where the side bet is slightly less ridiculous I'll have a way to get my fix of high-volatility gambling while not feeling like a complete fool.

To be continued!
link to original post

This is very interesting. Remember of course most 22's happen at a count of 0 because most of the time the count is 0 anyways. Better would be to compare the hit rate of true -1 to the hit rate of 0 etc. It only makes logical sense that a Hi-Lo counter would get more 22's at a negative count with a lack of 10's giving more combinations. As for Aces and Fives, I'm assuming the count is high when more 5's have been dealt than A's? I would say more aces lead to more soft hands which leads to less busts and therefore less 22's. Even If you dod gain an edge, these games are so volatile that you could possibly never notice a difference if you played your whole life. I ran a sidebet on this game called "pot of gold" and saw that 9's 10's and A's are bad for the player. With Hi-Lo just about any negative count made the side bet profitable. I wouldn't dare try and make money off this due to the volatility though. Good luck on your math quest

Quote: richodude

This is very interesting. Remember of course most 22's happen at a count of 0 because most of the time the count is 0 anyways.

What makes you think that most of the time the count is 0? I would say just the opposite, most of the time the count is not 0.

I think the average count is close to zero, but the number of occasions the count is actually zero is pretty small.

Quote: DRich

Quote: richodude

This is very interesting. Remember of course most 22's happen at a count of 0 because most of the time the count is 0 anyways.

What makes you think that most of the time the count is 0? I would say just the opposite, most of the time the count is not 0.
link to original post

Depends how zero is defined. I’m assuming the count is truncated meaning a running -7 between +7 (8 decks) is rounded to a true 0. Unless an ace five count is completely different. It would also make sense for a running 0 since we start a new count every 50 cards or so and most cards dealt don’t even affect the count.

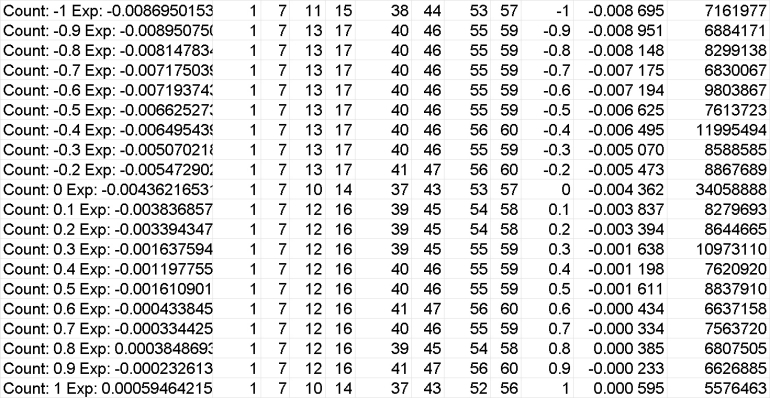If you're using a simple count then it's easy to get back to zero. This shows how during a run of 370m hands nearly 34m were at zero count, and half the hands were between -1 and 1.The program uses a simple Hi-Lo count, so uses the running count divided by the number of remaining decks, rounding down to one decimal point. It's impossible to get -0.1 as a count of -1 divided by 6 or smaller, cannot round down to -1/10.

The numbers I have seen so far indicate that a zero count is the least common of three scenarios (more aces, more fives or neither). I think this is because the number of unusual sequences that do not have the same number of Aces and Fives is much higher than the number of sequences that even out (ex: +11, -20, etc).

I think I will be able to publish the full notebook tomorrow, showing all numbers and charts. On the positive side, since I started this experiment I've played roughly 15h of Free Bet Black jack at the local casino and I could just be lucky but I've made a tidy profit on that side bet. It mostly hit at 7x but I got a few 20x and a couple 50x.

Interesting anecdote. At one point I was up to a $25 bet (increasing $5 every turn while the count remained 0) and the dealer shows a 4 of spades. Then a player to my left *hit* on a hard 15 (the dealer asked to confirm and the player confirmed); he got an 8 of spades. Bust. And then of course the dealer pulls a 10 of spades. I never blame other players usually but that dude prevented me from getting a $1,250 bonus. I walked away, went to play baccarat to cool down, and the pit boss showed up and told what just happened to the baccarat dealer, both were furious on my behalf :-)

I would also like to clarify that I do not work with a partner. When I mentioned adding another player I meant that I will run scenarios in my simulation that involve other simulated players just to see if it changes anything in the numbers I get. I prepared two simulated players profiles (one proper player and one typical casual player), I may put in another type of bad player that somehow seems to hang out a lot at this type of black jack table, the kind that "doesn't like to bust".

Stay tuned!

I'm still working on this analysis but I have preliminary results now that my simulator implements the full strategy described by Mike on his Free Bet webpage.

Interestingly the numbers show that my initial gut feeling (sweet spot on -2 count) was decent.

Both normal and push-22 rounds typically conclude when the count is between -2 and +2 (around 2/3 of the rounds) but within that bracket, the push-22 occurs more frequently on lower counts. At least according to my homemade simulation.

So until I get a chance to further this analysis, my own strategy will be to bet on that Push-22 side bet only when the Aces/Fives count is at -2, or possible -1 if I'm ahead.

Of course this is preliminary and either way I don't have actuarial skills so this is to be taken with a bag of salt.

I can't post links directly (the forum won't let me) but if you go on my site "enterprise-grade" dotcom you can see the charts and some more details by scrolling to the bottom for the article titled "Analyzing Free Bet Blackjack".

To be continued!

That’s awesome! Try and program it in a way where you aren’t focusing on only a five ace count. Be able to change the deck for every rank card. Maybe then you’ll discover the optimal count to be 2s and 7s or something. That is if you want to get serious about taking an advantage

Quote: jdmartin

I can't post links directly (the forum won't let me) but if you go on my site "enterprise-grade" dotcom you can see the charts and some more details by scrolling to the bottom for the article titled "Analyzing Free Bet Blackjack".

To be continued!
link to original post

Here is jdmartin's link:

Analyzing Free Bet Blackjack

In PA we just got Live dealer freebet blackjack - and they dont have the push 22 bet - but it is in Wind Creek casino