Rules are as follows:
- 8 decks
- S17
- DOA
- DAS
- RS4
- no RSAce
- early surrender against 10
- BJ pay 3:2
I got referred to a paper "Beyond Coupons" (PDF) by James Grosjean" on wizard site and found that similar rules (except 6 decks and late surrender) has expected return of $99.32 out of $100 wagered.
So how to derive the exact expected return using the above rules?
Is this a profitable game?
Quote: vulnerableGot a rolling chip program in a Macau casino. Buy $100000 and get $800 bonus, thus 0.8%.
Rules are as follows:
- 8 decks
- S17
- DOA
- DAS
- RS4
- no RSAce
- early surrender against 10
- BJ pay 3:2
I got referred to a paper "Beyond Coupons" (PDF) by James Grosjean" on wizard site and found that similar rules (except 6 decks and late surrender) has expected return of $99.32 out of $100 wagered.
So how to derive the exact expected return using the above rules?
Is this a profitable game?
link to original post
The expected return of this 8 deck, S17, ESvsTen game is 0.998113, the EV is -0.1887%. Given the 0.8% bonus on buy-in, you can draw your own conclusions.
So the person who buys in for $100,000 gets 100,800 in rolling chips. Winnings are paid in ordinary chips. So, you must *lose* all your rolling chips before you cash out. Since the probability of a loss in blackjack is about 0.48% and the average loss is 1.1 chips, that means each rolling chip is played on average 1.89 times. So the 100,800 generates about 191,000 in total initial wagers to lose the chips. At an EV of -0.189%, the player is losing about $360 in EV. That means the player should end up with an overall positive expected win of $800-$360 = $440. Based on the $191,000 in wagers, this amounts to a player edge of 0.23%.
Here is some of the data I used:
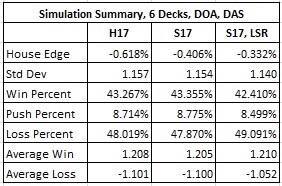
I've been suggesting rolling chips for blackjack for years here in the US. This is the first I heard of them in Macau. But yes, the player has an edge, but it's painfully small..
I know all your figures but the average loss being 1.1 chips. How do you get this figure?
Also, there is a trick. During surrender, you are forced to surrender ordinary chips and take back the original rolling chip bet.
For example, if you bet 100 rolling chip and surrender, you gave in 50 ordinary chip and take back 100 rolling chip.
How does this affect the edge?
https://www.888casino.com/blog/blackjack-tips/blackjack-combinatorial-analysis-by-simulation
As for your game in particular, including the surrender rule and other oddities, I would have to simulate that to get the edge. I don't know. But the answer is certainly not much different than my calculation above. In any real sense, your edge here is very small, even with minor rule changes. That said, if you have a game where you can back-bet and use a split-for-less strategy (like many Asian casinos offer), then that taken together with your rolling chips is certainly good enough.
Quote: vulnerable
Also, there is a trick. During surrender, you are forced to surrender ordinary chips and take back the original rolling chip bet.
For example, if you bet 100 rolling chip and surrender, you gave in 50 ordinary chip and take back 100 rolling chip.
How does this affect the edge?
link to original post
This is a huge advantage to you the player.
Quote: teliotAs for how I got to an average loss of 1.1 chips, you'll find that in this article of mine:
https://www.888casino.com/blog/blackjack-tips/blackjack-combinatorial-analysis-by-simulation
As for your game in particular, including the surrender rule and other oddities, I would have to simulate that to get the edge. I don't know. But the answer is certainly not much different than my calculation above. In any real sense, your edge here is very small, even with minor rule changes. That said, if you have a game where you can back-bet and use a split-for-less strategy (like many Asian casinos offer), then that taken together with your rolling chips is certainly good enough.
link to original post
In this particular casino only 1 bet is allowed in a box. So no rider strategy can be used.
Anyway thanks a lot for your reply.
Your ev = 401/210000 *100 = +0.191%
Quote: vulnerableYes I understand how rolling chips work.
I know all your figures but the average loss being 1.1 chips. How do you get this figure?
Also, there is a trick. During surrender, you are forced to surrender ordinary chips and take back the original rolling chip bet.
For example, if you bet 100 rolling chip and surrender, you gave in 50 ordinary chip and take back 100 rolling chip.
How does this affect the edge?
link to original post
I guess I am not understanding the mechanism here. When you bet $100 rolling chips and surrender that hand, are you required to bet $100 companying ordinary chips at the beginning of the hand? If yes, you have a good advantage here; if no, you have a bad disadvantage here.
Quote: acesideQuote: vulnerableYes I understand how rolling chips work.
I know all your figures but the average loss being 1.1 chips. How do you get this figure?
Also, there is a trick. During surrender, you are forced to surrender ordinary chips and take back the original rolling chip bet.
For example, if you bet 100 rolling chip and surrender, you gave in 50 ordinary chip and take back 100 rolling chip.
How does this affect the edge?
link to original post
I guess I am not understanding the mechanism here. When you bet $100 rolling chips and surrender that hand, are you required to bet $100 companying ordinary chips at the beginning of the hand? If yes, you have a good advantage here; if no, you have a bad disadvantage here.
link to original post
The dealer will take your one piece $100 rolling chip and return $50 rolling chip(from the chip tray).
Quote: ssho88Quote: acesideQuote: vulnerableYes I understand how rolling chips work.
I know all your figures but the average loss being 1.1 chips. How do you get this figure?
Also, there is a trick. During surrender, you are forced to surrender ordinary chips and take back the original rolling chip bet.
For example, if you bet 100 rolling chip and surrender, you gave in 50 ordinary chip and take back 100 rolling chip.
How does this affect the edge?
link to original post
I guess I am not understanding the mechanism here. When you bet $100 rolling chips and surrender that hand, are you required to bet $100 companying ordinary chips at the beginning of the hand? If yes, you have a good advantage here; if no, you have a bad disadvantage here.
link to original post
The dealer will take your one piece $100 rolling chip and return $50 rolling chip(from the chip tray).
link to original post
No. You give $50 ordinary chip to the dealer and get back the original $100 rolling chip bet.
Quote: acesideI guess this tiny catch may wipe out all your bonus edge.
link to original post
I have the same feeling, but not able to prove it.
Quote: vulnerableWe should keep surrendering. The strategy is not affected. Only that this causes the time to losing all rolling chips longer, thus affect the edge in favour of the casino.
link to original post
With ES10 rules, you will surrender about 6%(may not accurate) of your hand, so you have to bet 3%(6%/2) more, if your buy in is 100,000 + 800 = 100800 roling chips, you have to bet 100800/0.48 + 100800/0.48 *0.03/0.48 + + (100800/0.48 *0.03/0.48)*0.03/0.48 +..... = 210000 + 13125 + 820.3 +... = 224000, your expected loss = 224000 * 0.19 = 425.6, so your net win = 800 - 425.6 = 374.4.
Your ev = 374.4/224000 = +0.167%. I heard Macau have such similar promo ?
Also, to calculate the disadvantage from this bad surrender rule, we can also treat each surrender as a buy-in of additional 1.5-time rolling chips. If we know more details about the rules, we should be able to find this out.
Quote: ssho88Quote: vulnerableWe should keep surrendering. The strategy is not affected. Only that this causes the time to losing all rolling chips longer, thus affect the edge in favour of the casino.
link to original post
With ES10 rules, you will surrender about 6%(may not accurate) of your hand, so you have to bet 3%(6%/2) more,
link to original post
With the surrender rule as OP specified, I actually think the player should bet 9% more, which is 6%x1.5=9%.
Quote: acesideIím learning about this ES10 rule. Does this game have a dealer hole card? When the dealer shows an ace upcard, are the players allowed to early/late surrender?
Also, to calculate the disadvantage from this bad surrender rule, we can also treat each surrender as a buy-in of additional 1.5-time rolling chips. If we know more details about the rules, we should be able to find this out.
link to original post
No hole card and no surrender against dealer ace. And I forgot to mention that all BJ games in Macau use CSM.
I'm wondering if there are any other dead chip programs that are usable for BJ in Macau?


