Sette e Mezzo strategy

Playtech's new game Sette e Mezzo runs like this:

Each round is a new 40 card deck: 1-7. Jack, Cavalier, King in 4 suits. Numerical cards are worth their value, picture cards are worth 0.5 except the king of coins who is wild. (turns 7.0 or x.5 into 7.5, turns x.0 into 7, where x is less than 7)

The player and the dealer both get 1 card. The player is obligated to take more cards until his total is at least equal to the dealer, then he can choose to hit or stand. After the player stands, if the dealers card is 4 or less the dealer plays and will keep taking cards until he has 5 or higher. The aim is to get 7.5. If you get 8 or higher you bust. If player busts he loses regardless of dealer hand. If player and dealer end up on 5.0 dealer wins, if player/dealer match any other score it's a push, otherwise highest non bust hand wins.

What's best strategy for this game?

Quote: rumba434

Playtech's new game Sette e Mezzo runs like this:

Each round is a new 40 card deck: 1-7. Jack, Cavalier, King in 4 suits. Numerical cards are worth their value, picture cards are worth 0.5 except the king of coins who is wild. (turns 7.0 or x.5 into 7.5, turns x.0 into 7, where x is less than 7)

The player and the dealer both get 1 card. The player is obligated to take more cards until his total is at least equal to the dealer, then he can choose to hit or stand. After the player stands, if the dealers card is 4 or less the dealer plays and will keep taking cards until he has 5 or higher. The aim is to get 7.5. If you get 8 or higher you bust. If player busts he loses regardless of dealer hand. If player and dealer end up on 5.0 dealer wins, if player/dealer match any other score it's a push, otherwise highest non bust hand wins.

What's best strategy for this game?

Sette e Mezzo is actually Italian for seven-and-a-half and is a centuries old game, so this modification is based on that player-v-player game. The player-v-player version would essentially have no house edge (but would be skill-based) with the deal getting passed around from one player to the next.

The way the home version of this game worked is that each player (as well as the dealer) would have one face down card. Each player would take as many cards as they like, but they must show the face down card if they either bust or achieve 7.5, otherwise the face down card remains hidden until the dealer completes his play.*

After all the players had went, the dealer would reveal his face down card and would then draw as many cards as he wishes, until either busting or hitting the 7.5 total. In the home version of the game, the dealer not only wins with a higher score, but also wins all ties. Paying winning 7.5 at 2-1 was sometimes done and sometimes not, and a natural (two card) 7.5 beating one consisting of three, or more, cards was sometimes done and sometimes not.**

The rules of the Italian version allow for some degree of bluffing. A player, for instance, could not take any extra cards (even with a low card face down) in the hopes that the dealer would think it was a high card and try to score a higher total.

Anyway, my gut instinct is usually you would stand on 5.5 (or higher) and hit anything else against a lower dealer card*******, but I'm betting there are some exceptions. Even the exceptions will have exceptions that might be based on remaining deck composition if there are a lot of low cards out. I'll look at some of these individually tomorrow morning.

*https://en.wikipedia.org/wiki/Sette_e_mezzo
**http://www.blackjackforumonline.com/content/history-of-blackjack.htm

*******WRONG!!! TRUST THE MATH, NOT YOUR GUT!!!!

I saw this game in Uruguay. Here is my page on Siete y Media (seven and a half).

According to the site below the RTP is: 99.31% (when playing optimal strategy*** ).

***: I don't know what that is at the moment, but the "gut instinct" strategy in the post by Mission seems logical to me.

https://www.livedealer.org/blog/2020/05/ever-played-sette-e-mezzo/

Quote: Wizard

I saw this game in Uruguay. Here is my page on Siete y Media (seven and a half).

Thanks for the link. Do you think the fact its a 1-deck game, the presence of the king of coins, and the dealer win on ties of 5 would change the strategy any?

Quote: Wizard

I saw this game in Uruguay. Here is my page on Siete y Media (seven and a half).

It looks like one key difference is the player loses ties with a total of five in the Playtech version.

Another very important difference is that the player automatically must hit in the Playtech version if the player has less in total than the dealer. Because of that, some of the stands listed on that page the player literally could not do even if he wanted to. The player only has an actual decision to make if he has more than the dealer.

Quote: rumba434

Playtech's new game Sette e Mezzo runs like this:

Each round is a new 40 card deck: 1-7. Jack, Cavalier, King in 4 suits. Numerical cards are worth their value, picture cards are worth 0.5 except the king of coins who is wild. (turns 7.0 or x.5 into 7.5, turns x.0 into 7, where x is less than 7)

The player and the dealer both get 1 card. The player is obligated to take more cards until his total is at least equal to the dealer, then he can choose to hit or stand. After the player stands, if the dealers card is 4 or less the dealer plays and will keep taking cards until he has 5 or higher. The aim is to get 7.5. If you get 8 or higher you bust. If player busts he loses regardless of dealer hand. If player and dealer end up on 5.0 dealer wins, if player/dealer match any other score it's a push, otherwise highest non bust hand wins.

What's best strategy for this game?

Okay, so I feel like Wizard's page is going to give us a good starting point, so let's look at the situations where a player would stand under those rules:

2 v. 2

3 v. 1-3

3.5 v. 2-3

4 v. .5-4

4.5 v. 2-4

5 v. .5-4

Not included are situations where players would stand against a higher dealer total, because that's not allowed in this version.

The first one that is interesting to me given the push on five ties rule is the situation of 5 v. .5-4. We know that we would definitely choose to hit on 5 v. 5, because staying on that is definitely losing. But, if the dealer reaches a total of five, then we lose if we have stood on five.

Player (Natural) 5 v Dealer 4

---Player Stands

Okay, so the player has decided to stand pat on five, so let's look at all the different possible results for the dealer. Fortunately, this is relatively simple, because the dealer can only take a maximum of two more cards (otherwise would have more than five).

Remaining Deck:

1-4
2-4
3-4
4-3
5-3
6-4
7-4
J-4
C-4
K3 + WILD

Okay, so I assume the Wild King is automatically winning for the dealer. That leaves us with three possibilities for the first card: The dealer can win immediately with WILD or 1-3, the dealer busts with four or greater and the dealer draws again with 0.5.

Win Immediately: (13/38) = 0.34210526315

Lose Immediately: (14/38) = 0.36842105263

Draw Again: (11/38)---SEE BELOW

Okay, so if the dealer has to draw again, then what we are left with in the deck are 37 cards, but now 23 of those cards cause the dealer to win (.5 is now winning for the dealer with the five tie) whilst 14 of the cards remaining would cause the dealer to lose.

Draw Again-WIN: (11/38) * (23/37) = 0.17994310099

Draw Again-LOSE: (11/38) * (14/37) = 0.10953058321

Probability Dealer WIN: 0.34210526315 + 0.17994310099 = 0.52204836414

Probability Dealer LOSE: 0.36842105263 + 0.10953058321 = 0.47795163584

On the face of it, the dealer has a greater than 50% chance of winning, so now we have to see if drawing more cards would be worse for the player. For these purposes, I'm going to assume that the player is going to stand on a total of 5.5, or more.

Remaining Deck:

1-4
2-4
3-4
4-3
5-3
6-4
7-4
J-4
C-4
K3 + WILD

PLAYER HITS:

The first thing that we are going to point out is that the player will automatically lose with 3-7, so that's going to be 18/38 remaining cards right off the bat.

(18/38) = 0.47368421052

As we can see, that's a pretty substantial likelihood of the player hitting and losing immediately. With that, let's look at the second most likely scenario, the player hits for a .5 point card, stands and the dealer draws:

We start with the probability of hitting for a half point card at (11/38), so now we have the following remaining deck composition for the dealer to hit his four, I'm going to pretend the player got a Jack just because it really doesn't make a difference which one it is.

1-4
2-4
3-4
4-3
5-3
6-4
7-4
J-3
C-4
K3 + WILD

Okay, so now the player has a 5.5 against the dealer four. In addition to 4-7, the dealer also loses immediately if he draws a 1 because that would give the dealer a total of five. If the dealer draws a 2, 3 or wild, then the dealer wins immediately. Play, once again, only continues beyond this if the dealer draws a .5 card.

Dealer wins immediately:

(11/38) * (9/37) = 0.07041251778

So, we look at this: 0.07041251778 + 0.47368421052 = 0.5440967283

Okay, so our probability of the dealer winning if we stand was only 0.52204836414 and the probability of the player busting if he hits + the player hitting a .5 card and then the dealer winning on the very next card combines to be more than the probability of the dealer winning if we stand.

Similarly, we will demonstrate that the player should not hit on the 5.5 in this situation because of the probability of busting on the following card, which would be a 3 or higher causing a bust:

Player 5.5-Dealer 4, player hits again:

(11/38) * (18/37) = 0.14082503556

Once again, just given the possibility of the player busting and ignoring everything else that could happen, the player ends up with a greater probability of losing (combined with the first hit) than if the player had just stood on 5 v. 4 in the first place. We thought that maybe ties on five losing could make the difference compared to the Wizard's write up on the other version of this game, but it does not.

Multi-Card 5's v. Dealer's 4

There is no need to do anything with this because a multi-card five will generally make it more likely that the dealer busts by hitting his four. The reason why is because more cards that do not bust the dealer will have been eliminated from the deck. Remember, 4-7 busts the dealer immediately and we were already starting with a five in the original example. The only multi-card five that takes away a dealer bust card (and then still only one) is the combination 4-.5-.5 or 4-1. All other multi-card fives would actually increase the number of cards the dealer can bust on, thereby making the situation better for the player.

Okay, the next situation we are going to look at will involve a Player 4 v. a Dealer 4. This is going to be fairly simple to analyze for the player standing because we simply have the dealer taking only one card, or taking a half point card and then another card and there are no other possibilities:

Player 4 v. Dealer 4--Player Stands.

Remaining Deck Composition:

1-4
2-4
3-4
4-2
5-4
6-4
7-4
J-4
C-4
K3 + WILD

The probabilities for the dealer are actually exactly the same, because all we have done is exchanged a five for a four, which from a probabilistic standpoint, doesn't change anything. We can copy from above:

Okay, so I assume the Wild King is automatically winning for the dealer. That leaves us with three possibilities for the first card: The dealer can win immediately with WILD or 1-3, the dealer busts with four or greater and the dealer draws again with 0.5.

Win Immediately: (13/38) = 0.34210526315

Lose Immediately: (14/38) = 0.36842105263

Draw Again: (11/38)---SEE BELOW

Okay, so if the dealer has to draw again, then what we are left with in the deck are 37 cards, but now 23 of those cards cause the dealer to win (.5 is now winning for the dealer) whilst 14 of the cards remaining would cause the dealer to lose.

Draw Again-WIN: (11/38) * (23/37) = 0.17994310099

Draw Again-LOSE: (11/38) * (14/37) = 0.10953058321

Probability Dealer WIN: 0.34210526315 + 0.17994310099 = 0.52204836414

Probability Dealer LOSE: 0.36842105263 + 0.10953058321 = 0.47795163584

On the face of it, the dealer has a greater than 50% chance of winning, so now we have to see if drawing more cards would be worse for the player. For these purposes, I'm going to assume that the player is going to stand on a total of 5.5, or more.

Player 4 v. Dealer 4-Player hits

Okay, so in this scenario, the player is going to take a card. The first thing that we want to consider is the probability that the player does this and simply busts immediately. This is the same as for the dealer (4-7), consists of 14 cards and can be taken from above:

Lose Immediately: (14/38) = 0.36842105263

There are fewer busts in this scenario, but what we do know from the previous thing is that the player should stand on any total of five, or greater, because Player 5 v. Dealer 4---STAND would not be true otherwise, and we know it is true.

So, with that, let's look at the most likely hit for the player, which is hitting for a half point card, and analyze whether the player should stand or hit again:

***Player 4 + .5 v. Dealer 4***

***Player Hits***

1-4
2-4
3-4
4-2
5-4
6-4
7-4
J-3
C-4
K3 + WILD

Okay, so the first thing is that the player had a probability of 11/38 to even get a half point card in the first place. At this point, 4-7 will still bust the player, so let's take a look at that:

(11/38) * (14/37) = 0.10953058321

Okay, so now we add that to the 0.36842105263 probability that the player just loses right away and end up with 0.47795163584.

Even in this scenario, the player has a probability of 10/37 of just hitting for another half point card, which results in a total of five that we know the player stands. Obviously, that's also going to be pretty bad news for the player. Let's look at that:

(11/38) * (10/37) = 0.07823613086

Okay, so that's the probability that the player is going to hit and get two half point cards in a row. Our remaining deck composition will be as such for the dealer to draw:

1-4
2-4
3-4
4-2
5-4
6-4
7-4
J-2
C-4
K3 + WILD

The dealer draws to a four, so the possibilities are as follows:

Lose Immediately: (14/36) = 0.38888888888
Win Immediately: (13/36) = 0.36111111111
Draw Again: (9/36) = 0.25

As we predicted, with more small cards removed from the deck, the probability of the dealer hitting and losing immediately is increased. In this specific case, however, we have only removed 'Draw again' half point cards, so the probability of the dealer winning immediately also increased a little bit.

Now, we will imagine that the dealer draws another jack, just for fun we'll make them all jacks, and then has to draw again. At this point, half point cards result in the dealer winning with a total of five. 4-7 still cause a bust:

(9/36 * 14/35) = .1

(9/36 * 21/35) = .15

Okay, now we have to work back in the probability of any of this happening in the first place after we do our total probabilities in this specific situation.

Player 4 v. Dealer 4, Player Hits Gets .5, Player Hits Again Gets .5:

Dealer Wins: .15 + 0.36111111111 = .511111111

Dealer Loses: .1 + 0.38888888888 = .48888888888

Probability of Player 4 + .5 + .5 = 0.07823613086 (From Above)

0.07823613086 * .511111111 = 0.03998735576 (Dealer Wins)

0.07823613086 * .488888888 = 0.03824877501 (Dealer Loses)

0.47795163584 + 0.03998735576 = 0.5179389916 (In this scenario of the player hitting 4 and busting, hitting 4 getting .5 and busting or hitting 4, getting .5, hitting again and getting .5 and then losing by standing, we are so close to the probability of the dealer winning if we just stand and let the dealer go that the dealer beating other totals such as 5.5 or 6.5 is pretty clearly going to exceed our probability of losing if we just let the dealer try to bust, instead). Hitting the 4.5 is a bad decision and we need go no further with that.

Player 4 v. Dealer 4, Player Hits and Gets .5---Stands

Okay, so we're now going to have the player stand on 4.5 instead, so let's look at the remaining deck composition:

***Player Stands***

1-4
2-4
3-4
4-2
5-4
6-4
7-4
J-3
C-4
K3 + WILD

Once again, the player had a 11/38 probability of getting a half point card in the first place, so that's going to be our starting point. We also know that the player had a:

Lose Immediately: (14/38) = 0.36842105263

So, we're going to look specifically at the player hitting, getting a .5 card and standing with 4.5 against the dealer 4. We're making the .5 card a Jack again. It's always a Jack. The Jack has a 100% probability of coming out. (LOL)

Okay, so the dealer is in the same situation he's always in. The dealer will now have the following probabilities:

Win Immediately: (13/37) = 0.35135135135
Lose Immediately: (14/37) = 0.37837837837
Hit Again (0.5): (10/37) = 0.27027027027

Okay, so now we just have to look at the probability of the dealer drawing the .5 card and then winning or losing. As you'll recall, another half point card is winning for the dealer:

Dealer Wins (10/37 * 22/36) = 0.16516516516
Dealer Loses (10/37 * 14/36) = 0.1051051051

Total Dealer Wins: 0.35135135135+0.16516516516 = 0.51651651651
Total Dealer Loses: 0.37837837837+0.1051051051 = 0.48348348347

Okay, now we just need to work back in our probability of the player getting a half point card in the first place:

(11/38) * 0.51651651651 = 0.14951793899 (Dealer Wins)
(11/38) * .48348348347 = 0.13995574521 (Dealer Loses)

So, we add the dealer win probability to our probability that the player takes that first hit and busts to begin with and get:

0.36842105263+0.14951793899 = 0.51793899162

How about that!? The player is equally likely to lose this way as the player is to hit the 4.5, get another .5 card, and then stand on 5. That's pretty wild, isn't it?

And, as we have already established, the player always stands on a total of five against a dealer four.

Once again, we could do all of the work to factor in the player ending up with other totals (that are more than five) and still losing, but let's recall that the player standing on four results in a probability of:

0.52204836414 of the dealer winning, so if we do this:

0.52204836414-.51793899162 = 0.00410937252

So, we would only need combined probabilities of 0.410937252%, or more, of the player losing on a total of more than five to make the overall decision to hit on the four to begin with a worse decision. I could mathematically prove that this is the case, but it's so obvious already---and this is already taking forever---that I'm not going to waste the time doing that.

CONCLUSION

Player 4 v. Dealer 4

--The player should stand and hope for the dealer to bust.

Let's take a quick breather and see where we are at so far:

Player Total x v. Dealer Total x:

The Player has no choice but to hit if the player's total is less than that of the dealer:

Player Total 5 v. Dealer Total 5:

Technically, the player does not have to hit, but should hit unless he wants to lose.

Player Total 5 v. Dealer Total 4:

The player should STAND and hope for the dealer to bust.

Player Total 4 v. Dealer Total 4:

The player should STAND and hope for the dealer to bust.

Player Total 4.5 v. Dealer Total 4:

The Player should STAND and hope for the dealer to bust. We didn't do the math on this, but because 4 v. 4 STAND is true and 5 v. 4 STAND is true, this must also be true. Also relevant, this removes an extra .5 card from the deck which is a card that does NOT bust the dealer, so that's good for the player.

Okay, let's get a couple things out of the way really quick. We're going to demonstrate very quickly that the Player never hits a six unless he has no other choice:

Player 6 v. Dealer Less Than Six

Deck Composition (I'm giving the dealer a four, which is a best case scenario for the player other than a five, which would mean the player had already won)

1-4
2-4
3-4
4-3
5-4
6-3
7-4
J-4
C-4
K3 + WILD

Okay, so we start with the fact that 22 cards bust the player. (22/38) = 0.57894736842

That's more than half, so the player should stand. As we already know, the dealer has a greater probability of busting than the player's (1-0.57894736842) = 0.42105263158 probability of improving his hand, which doesn't even guarantee that the player wins. We will prove this because it is easy:

Dealer Busts or Totals 5 and loses immediately: (18/38) = 0.47368421052

There you have it, the dealer is more likely to bust than the player is to even improve his hand by taking a hit. Standing is clearly the correct decision.

Due to the high probability of the player busting by taking a card, the player standing on six will be the correct decision against any dealer total that is not greater than six.

Because the probability of the player busting is more than .5, the expected loss of that decision is more than zero. Because the expected loss of that decision is more than zero, the player should take the push on the total of Player 6 v. Dealer 6. Similarly, the player should take the Push on Player 7 v. Dealer 7.

With that, let's look at our strategy that we know so far:

Hitting Decisions:
Player .5 v. Dealer .5 (ANY)---The player can only improve his hand and cannot possibly bust.
Player x v. Dealer x (More than Player)---You must hit.
Player 5 v. Dealer 5---The player doesn't technically have to hit, but the alternative is automatically losing by standing.--So HIT. If the player hits and does not bust, then the player automatically wins, so the player would stand after this.

Standing Decisions:
Player 4 v. Dealer 4---The player should stand as previously demonstrated.
Player 4.5 v. Dealer 4---Because the player should stand on Player 4 v. Dealer 4, it must be true that the player should stand here.
Player 5 v. Dealer 4---The player should stand as previously demonstrated.
Player 5.5 v. Dealer 5---The player automatically wins and should stand.
Player 5.5 v. Dealer 4---Because standing on five against a Dealer 4 is true, and this is automatically better (Player wins against Dealer 5) this must be true.
Player 6 v. Dealer (6 or less)---The Player should stand. Just the probability of losing by hitting gives this play a negative expected value.
Player 7 v. Dealer (7 or less)---Obviously, the player should stand.

To Be Determined:

Player 5.5 v. Dealer .5-3

Player 5 v. Dealer .5, 1, 2 and 3

Player 4 v. Dealer .5, 1, 2 and 3

Player 3 v. Dealer .5, 1, 2 and 3

Player 2 v. Dealer .5, 1 or 2

Player 1 v. Dealer .5 or 1

Great work so far Mission!

My guess is that either the Wizard's table will completely hold up, or it will fail on 4.5 vs dealer 1, 4.5 being a weaker hand to hit as it has a good chance of turning into 5, which is not a better hand in this game but is in Wizard's table.

With all of that out of the way, let's work on our next borderline case; Player 5 v. Dealer 3.

In this case, the dealer has fewer cards that will bust him immediately as compared to Player 5 v. Dealer 4, and a push still loses, so this is going to end up being a closer decision mostly due to the fact that the dealer has more ways to get to a total of five.

Player 5 v. Dealer 3---Player Stands

The first thing that we are going to look at is the expected result of the player standing, this is going to be somewhat easy because we only have to look at results that will end up with the dealer winning against the player. We can start with the fact that the dealer hitting for a two, three, four or wild wins immediately:

Remaining Deck:

1-4
2-4
3-3
4-4
5-3
6-4
7-4
J-4
C-4
K3 + WILD

We will also see that only 5-7 will cause the dealer to lose immediately, with all other results ending up with play continuing.

Win Immediately: (12/38) = 0.31578947368

Lose Immediately: (11/38) = 0.28947368421

Draw Again: (15/38)---SEE BELOW

The cards that will result in the dealer drawing again are the half point cards (11) and ones (4) for a total of fifteen cards. This is going to get a bit more messy because there are so many combinations of possibilities after this. We are going to start with the dealer drawing a one (4/38) which will result in a total of four and play continuing:

If the dealer has a new total of four, then the three possibilities are that the dealer hits again and wins immediately (1, 2, 3, W) that the dealer hits again and busts (4, 5, 6, 7) or that the dealer hits a half point card and continues hitting (.5). Let's update our deck composition:

Remaining Deck:

1-3
2-4
3-3
4-4
5-3
6-4
7-4
J-4
C-4
K3 + WILD

Dealer Wins Immediately: (4/38 * 11/37) = 0.03129445234

Dealer Loses Immediately: (4/38 * 15/37) = 0.0426742532

Play Continues: (4/38 * 11/37) = 0.03129445234

Okay, so now we are going to remove a Jack, because it will always be a jack, and look at what happens when play continues.

Remaining Deck:

1-3
2-4
3-3
4-4
5-3
6-4
7-4
J-3
C-4
K3 + WILD

In this case, the dealer can only take one more card, because every single card results in a total of five, or greater, so the dealer can only win or bust.

Dealer Wins: (0.03129445234 * 21/36) = 0.01825509719

As we know, 4-7 now bust the dealer at this point, so that will be the other 15 remaining cards:

Dealer Loses: (0.03129445234 * 15/36) = 0.01303935514

Okay, so now we total our probabilities:

Dealer Wins: 0.31578947368 + 0.01825509719 + 0.03129445234 = 0.36533902321

Dealer Loses: 0.28947368421 + 0.0426742532 + 0.01303935514 = 0.34518729255

TBD: 1 - (0.34518729255+.36533902321) = 0.28947368424

Probability Dealer Hits for .5 Card: (11/38) = 0.28947368421

So, as you can see, we're on the right track with an extremely minor rounding error. With this, we must look at all of the things that can happen when the dealer hits and receives the .5 card. As we know, the dealer must hit again if this happens.

The .5 card is now assumed, which means that we take a jack out of the deck because jacks come out with a 100% probability. The dealer's total is now 3.5, so we have to look at all of the possible scenarios.

Remaining Deck:

1-4
2-4
3-3
4-4
5-3
6-4
7-4
J-3
C-4
K3 + WILD

As we see, the five that belongs to the player has been removed, the three that belongs to the dealer has been removed and the jack that now belongs to the dealer has been removed. The dealer has a total of 3.5 and automatically loses with 5-7, automatically wins with 2-4 (or wild) and play continues with another .5 or 1 card.

Dealer Wins: (11/38) * (12/37) = 0.09388335704

Dealer Loses: (11/38) * 11/37) = 0.08605974395

Play Continues: (11/38 * 14/37) = 0.10953058321

Okay, so let's go ahead and recalculate our total probabilities and make sure that 7.43%~ represents everything else.

Dealer Wins: 0.36533902321 + .09388335704 = 0.45922238025

Dealer Loses: 0.34518729255 + .08605974395 = 0.4312470365

Remaining: 1 - (0.45922238025 + .4312470365) = 0.10953058325

***FINALLY!!! The reason I keep updating this is because it lets me know if I have made a mistake, which I did, by forgetting to put the one from before back in the deck. It took me forever to figure that out as it was, imagine if I hadn't been checking as I went along!

Okay, so now we have the dealer sitting on either a total of four or a total of 4.5 and he must draw again. Let's go ahead and give the dealer a three-card 4.5 that went like this: 3 + .5 + 1.

(11/38 * 4/37) = 0.03129445234

Right, and now what I am going to do is update the remaining deck composition correctly this time, which should make it much easier for me.

Remaining Deck:

1-3
2-4
3-3
4-4
5-3
6-4
7-4
J-3
C-4
K3 + WILD

Okay, so we have the dealer sitting on 4.5 that occurs in the order 3 + .5 + 1 with 0.03129445234 probability of drawing the half card then drawing the one. At this point, the dealer can only win or lose. .5-3 + W is winning (21/36) and 4-7 are losing (15/36)

Dealer Wins: .03129445234 * 21/36 = 0.01825509719

Dealer Loses: .03129445234 * 15/36 = 0.01303935514

Good times. Let's update our totals:

Dealer Wins: 0.45922238025 + .01825509719 = 0.47747747744

Dealer Loses: 0.4312470365 + .01303935514 = 0.44428639164

Remaining: 1 - (.47747747744 + .44428639164) = 0.07823613092

Dealer .5 + .5 = 4 --- (11/38 * 10/37) = 0.07823613086

Very good!

Okay, so now the dealer has a total of 4 via 3 + .5 + .5. It will always be a jack. Let's look at our remaining deck composition:

Remaining Deck:

1-4
2-4
3-3
4-4
5-3
6-4
7-4
J-2
C-4
K3 + WILD

Okay, so the first thing I'm going to do is actually put the one back this time. It turns out having the right cards in the deck is kind of important.

Brevity aside, the dealer is now sitting on a three-card total of four and must take a hit. 1-3 + WILD wins immediately, 4-7 loses immediately and play continues with another .5 card. Let's do it:

Dealer Wins: 0.07823613086 * (12/36) = 0.02607871028

Dealer Loses: 0.07823613086 * (15/36) = 0.03259838785

Play Continues: 0.07823613086 * (9/36) = 0.01955903271

Let's update our totals:

Dealer Wins: 0.47747747744 + 0.02607871028 = .50355618772

Dealer Loses: 0.44428639164 + 0.03259838785 = 0.47688477949

Remaining: 1 - (.50355618772 + .47688477949) = 0.01955903279

In our final scenario, the dealer has really decided to make you sweat. You have decided to stand your five against the dealer three, and this dealer has decided to pull three half point cards out in a row, and just for style points, they were all jacks. Let's update our deck composition:

Remaining Deck:

1-4
2-4
3-3
4-4
5-3
6-4
7-4
J-1
C-4
K3 + WILD

The dealer has a four card total of 4.5 and there are 35 cards remaining in the deck. The dealer will now win with any total of .5-3 or WILD (20/35) and will lose with 4-7 (15/35). Let's see how this plays out:

Dealer (Finally!) Wins: 0.01955903279 * (20/35) = 0.01117659016

Dealer (Mercifully!) Loses: 0.01955903279 * (15/35) = 0.00838244262

FINAL PROBABILITIES

Dealer Wins: .50355618772 + .01117659016 = 0.51473277788

Dealer Loses: 0.47688477949 + 0.00838244262 = 0.48526722211

1 - (0.48526722211+.51473277788) = 1.0000001e-11 (So, 0).

CONCLUSION

On its face, it seems weird that the dealer has a reduced probability of winning starting with a three against a player standing five than he does with a four, but it's actually not. What we see in this situation is that the dealer's overall bust rate is going to increase in this scenario. Remember, the player only wins if the dealer busts because a tie on five is a loss.

What ends up happening in this case is that the dealer ends up with more potential opportunities to bust because ONES no longer cause the dealer to immediately win, as the dealer would if he was hitting a four.

At the same time, it's true that fours no longer immediately cause the dealer to bust (hitting on three) as they would with four, but in the case of hitting on four, the dealer also already has a four which itself removes a bust card from the deck.

So, as it unusual as it might seem, the player standing on five would rather go against a dealer three than a dealer four, though the total difference is pretty negligible. Let's see in the next post if the player is better off to hit 5 against dealer 3, though I very much doubt it.

Quote: rumba434

Great work so far Mission!

My guess is that either the Wizard's table will completely hold up, or it will fail on 4.5 vs dealer 1, 4.5 being a weaker hand to hit as it has a good chance of turning into 5, which is not a better hand in this game but is in Wizard's table.

Thanks!

This is a pretty fun one and not hard to do, aside from being time-consuming. The good news for me is I can make an LCB article about this game and reuse all of this math, so it's not a fruitless endeavor for me.

The 4.5 one is an interesting case because it requires hitting on something else to even get to it. As we have already determined, you do not hit a 4 against a 4 because it's more likely to win just hoping for the dealer to bust. So, if 4.5 is going to be reached at all, it will be incorporated into the decision already made to hit on .5 (which we know you do) 1, 2 or 3. The latter of those three things require that the player already has multiple cards, and even when that happens, you're often hitting because the dealer has a higher total to begin with, so you must hit.

By the way, is there only one player spot for this game and all players use the same cards, or is it possible for multiple players to all sit at the same table and get different hands?

In the Playtech version, it's all versus dealer. There is currently no multi-seat version, and probably never will be.

Quote: rumba434

In the Playtech version, it's all versus dealer. There is currently no multi-seat version, and probably never will be.

I would think not. ;)

Player 5 v. Dealer 3---Player Hits

Okay, so now we have to consider what might happen if the player decides to hit his 5 against a dealer three. Let's first look at the remaining deck composition:

Remaining Deck:

1-4
2-4
3-3
4-4
5-3
6-4
7-4
J-4
C-4
K3 + WILD

As we know, totals of 3-7 are going to immediately bust the player in this situation, so let's determine that probability:

(18/38) = 0.47368421052

From the previous analysis of standing Player 5 against Dealer 3, we recall that the dealer had an overall probability of winning of 0.51473277788, so we're not too far from reaching that (and rendering all other possibilities moot) just from the probability of the player busting.

What will knock a pretty good chunk out of this is let's have the player hit and receive a 1 (obvious stand) with the dealer hitting for a four and beating the player 6 to 7:

Player 5, hits for one, stands on six: (4/38) = 0.10526315789

Dealer 3, hits for four or wild, wins 6-7: 0.10526315789 * (5/37) = 0.01422475106

Okay, so we combine those things with the probability of the player just busting and: 0.01422475106 + .47368421052 = 0.48790896158

The next thing we are going to do is look at the specific situation of a player hitting for a 1 and getting a total of 6, but then the dealer hits for .5 followed by a hit for 3 or 4 or WILD and wins:

Player 5, hits for one, stands on six: (4/38) = 0.10526315789

Dealer Three, Hits for .5, Total 3.5 and hits 3-4-W: .10526315789 * (11/37 * 8/36) = 0.00695432274

Okay, so now we take our new total: 0.48790896158 + 0.00695432274 = 0.49486328432

Player Hits 5 and ends up with 5.5, hits again

Unfortunately (for me) the probability of the player hitting to six and losing quickly + the probability of the dealer busting was insufficient to prove our point. Therefore, now what we are going to do is have the player hit and receive a .5 value card. The probability of the hit resulting in this total is (11/38)

Our remaining deck composition will be this:

1-4
2-4
3-3
4-4
5-3
6-4
7-4
J-3
C-4
K3 + WILD

Okay, so the first thing that we are going to do is demonstrate that the player should not hit again due to the probability of busting alone. Sitting on a total of 5.5, we see that 3-7 now busts the player. The probability of that with what remains is (18/37), so we will combine that with our (11/38) of the player getting a .5 value card to begin with:

(11/38 * 18/37) = 0.14082503556

We will remember from above that the probability of the player busting hitting to a 5 in the first place was 0.47368421052, so if we add the probability of this sequence of events if the player hits on 5.5 against a dealer three:

0.47368421052 + .14082503556 = 0.61450924608

Therefore, we know hitting on 5.5 (after hitting on five and receiving the .5 card) is an obviously terrible decision and, in comparison, the player was much better off to stand on 5 in the first place.

Player Hits 5 and ends up with 5.5, stands

We already know that the player should not hit on 5.5 because that is worse than standing on 5 would have been in the first place. Because of this, we know that the player should stand on 5.5, but should he have ever hit to begin with?

Let's recall our new deck composition:

Our remaining deck composition will be this:

1-4
2-4
3-3
4-4
5-3
6-4
7-4
J-3
C-4
K3 + WILD

Okay, so now we have stood on 5.5 and the action is back to the dealer who has a three. We will recall that the probability of the player hitting the 5 and getting a half point card in the first place was (11/38), so we have 37 cards remaining and that 11/38 will carry over to this.

The dealer, with a total of three, will win immediately with either a three or a four, that represents (7/37) remaining cards:

(11/38 * 7/37) = 0.0547652916

Okay, so let's add our known probabilities from before.

Player hits on 5 and busts immediately: 0.47368421052

Player hits on 5, gets .5, stands on 5.5 and loses immediately to 6 or 7: 0.0547652916

0.0547652916 + 0.47368421052 = 0.52844950212

We will recall from the Stand on 5 against Dealer 3 section that the probability of the dealer beating the player was 0.51473277788, all things considered.

What that means is, just going off of hitting 5 and receiving a .5 card alone (or busting) the player is automatically worse off by hitting again, or by standing on a total of 5.5, than he would have been if he had never hit on 5 in the first place.

As a result, standing on 5 v. Dealer 3 is the superior decision and we can update our strategy accordingly:

Hitting Decisions:
Player .5 v. Dealer .5 (ANY)---The player can only improve his hand and cannot possibly bust.
Player x v. Dealer x (More than Player)---You must hit.
Player 5 v. Dealer 5---The player doesn't technically have to hit, but the alternative is automatically losing by standing.--So HIT. If the player hits and does not bust, then the player automatically wins, so the player would stand after this.

Standing Decisions:
Player 4 v. Dealer 4---The player should stand as previously demonstrated.
Player 4.5 v. Dealer 4---Because the player should stand on Player 4 v. Dealer 4, it must be true that the player should stand here.
Player 5+ v. Dealer 3---The player should stand.
Player 5+ v. Dealer 4---The player should stand as previously demonstrated.
Player 5.5+ v. Dealer 5---The player automatically wins and should stand.
Player 5.5+ v. Dealer 4---Because standing on five against a Dealer 4 is true, and this is automatically better (Player wins against Dealer 5) this must be true.
Player 6 v. Dealer (6 or less)---The Player should stand. Just the probability of losing by hitting gives this play a negative expected value.
Player 7 v. Dealer (7 or less)---Obviously, the player should stand.

To Be Determined:

Player 5.5 v. Dealer .5-2

Player 5 v. Dealer .5, 1, 2

Player 4 v. Dealer .5, 1, 2 and 3

Player 3 v. Dealer .5, 1, 2 and 3

Player 2 v. Dealer .5, 1 or 2

Player 1 v. Dealer .5 or 1

Quote: Wizard

I saw this game in Uruguay. Here is my page on Siete y Media (seven and a half).

On your basic strategy chart for siete-y-media, you show a players hand of 6.7 -obviously it should be 6.5. Probably too hard to fix -its not worth it.

PLAYER 5 v. DEALER 2---.PLAYER STANDS

We're going to go ahead and stay with the Player 5's here and look at the player starting with 5 against a dealer 2. The first thing that we are going to want to know is our deck composition:

Remaining Deck:

1-4
2-3
3-4
4-4
5-3
6-4
7-4
J-4
C-4
K3 + WILD

As before, analyzing the player standing is the easiest because only the dealer has to take an action. Because we have already done the full breakdown on so many things, we're also going to take a little shortcut. The shortcut is that we are ONLY going to look at all of the different ways the dealer can bust (since his actions are fixed) and know that (1-Dealer Bust) is the probability of the dealer winning.

Right, so the dealer has a total of 2 and either a six or a seven busts him immediately:

(8/38) = 0.21052631578

Okay, now we are going to pretend that the dealer gets another 2, and with a new total of four, receives 4-7 for a bust:

(3/38) * (15/37) = 0.0320056899

Glorious! Now, we will have the dealer receive a two, followed by a half point card, followed by a 4-7 for a bust:

(3/38) * (11/37) * (15/36) = 0.00977951635

Phenomenal! The dealer can also hit for a 1, followed by a 5-7 and bust that way:

(4/38) * (11/37) = 0.03129445234

Spectacular! The dealer can hit his two, get a 1, get another 1, then get 4-7:

(4/38 * 3/37 * 15/36) = 0.00355618776

Serendipitous! The dealer can also go 2-1-1-.5-(4-7)

(4/38 * 3/37 * 11/36 * 15/35) = 0.00111765901

Outstanding! Let's go ahead and do a quick recap, then we will look at all of our combinations that start with 2 + 0.5:

BUST: 0.21052631578

2 + 2 + BUST: 0.0320056899

2 + 2 + .5 + BUST = 0.00977951635

2 + 1 + BUST: = 0.03129445234

2 + 1 + 1 + BUST = 0.00355618776

2 + 1 + 1 + .5 + BUST = 0.00111765901

Okay, let's add all of these up:

0.21052631578+0.0320056899+0.00977951635+0.03129445234+0.00355618776+0.00111765901 = 0.28827982114

Magnificent! Okay, now we have to do some other combinations involving 2 + 1:

With all of our 2 + 2 and 2 + 2 + .5 combinations and 2 + 1 + 1 possibilities out of the way, we must move on to possibilities that would have 2 + 1 + .5, then we can move on to our 2 + .5 variations.

In order to simplify things, let's start with a base probability for 2 + 1 + .5 and a new deck composition:

(4/38 * 11/37) = 0.03129445234

Remaining Deck:

1-3
2-3
3-4
4-4
5-3
6-4
7-4
J-3
C-4
K3 + WILD

You knew it would be a jack.

Right, so we have a dealer total of 3.5 via 2 + 1 + .5, which comes with a probability of 0.03129445234, so let's go ahead and work from that.

Given the total of 3.5, we know that 5-7 are an immediate bust:

0.03129445234 * (11/36) = 0.00956219377

Fantastic! So, now we are going to do 3.5 + 1 + 4-7 for a bust:

0.03129445234 * (3/36) * (15/35) = 0.00111765901

Astounding! There is no other possible 3.5 + 1 bust combination in this line because the next card either wins or loses on a 4.5 total.

The next thing we have to look at will be 2 + 1 + .5 + .5 + .5 bust with 4-7 after:

0.03129445234 * (10/36 * 9/35 * 15/34) = 0.00098616971

Neat! Okay, let's do the more likely 2 + 1 + .5 + .5 bust with 4-7 after:

0.03129445234 * (10/36 * 15/35) = 0.00372553004

Terrific! I think we're ready to total our busts again:

0.28827982114+0.00956219377+0.00111765901+0.00098616971+0.00372553004 = 0.30367137367

Let's recap everything that we have done starting with the two:

BUST (2): 0.21052631578

2 + 1 + BUST: (3) = 0.03129445234

2 + 1 + .5 + BUST (3.5) = 0.00956219377

2 + 2 + BUST (4): 0.0320056899

2 + 1 + 1 + BUST (4)= 0.00355618776

2 + 1 + .5 + .5 + BUST (4) = 0.00372553004

2 + 2 + .5 + BUST (4.5) = 0.00977951635

2 + 1 + 1 + .5 + BUST (4.5) = 0.00111765901

2 + 1 + .5 + 1 + BUST (4.5) = 0.00111765901

2 + 1 + .5 + .5 + .5 + BUST (4.5) = 0.00098616971

Total So Far: 0.21052631578+0.03129445234+0.00956219377+0.0320056899+0.00355618776+0.00372553004+0.00977951635+0.00111765901+0.00111765901+0.00098616971 = 0.30367137367

Supercalifragilisticexpialidocious!!! Now all we have to do is determine all of our bust combinations that start with 2 + .5.

TOTAL PROBABILITY CARRIED FORWARD: 0.30367137367

Next Card .5 Probability: (11/38) = 0.28947368421

Remaining Deck Composition (37 Cards):

1-4
2-3
3-4
4-4
5-3
6-4
7-4
J-3
C-4
K3 + WILD

So, the first thing that we are going to do is actually take the time to list every scenario that results in a bust from a starting state of 2.5. I'm doing this now so that I don't have to triple check this nine different times like I did above.

2.5 + 6/7 = BUST (2.5)--->0.28947368421 * (8/37) = 0.06258890469

2.5 + .5 + 5-7 = BUST (3)--->0.28947368421 * (10/37 * 11/36) = 0.02390548443

2.5 + .5 + .5 + 5-7 = BUST (3.5)--->0.28947368421 * (10/37 * 9/36 * 11/35) = 0.00614712456

2.5 + 1 + 5-7 = BUST (3.5)--->0.28947368421 * (4/37 * 11/36) = 0.00956219377

2.5 + .5 + .5 + .5 + 4-7 = BUST (4)--->0.28947368421 * (10/37 * 9/36 * 8/35 * 15/34) = 0.00197233943

2.5 + .5 + 1 + 4-7 = BUST (4)--->0.28947368421 * (10/37 * 4/36 * 15/35) = 0.00372553004

2.5 + 1 + .5 + 4-7 = BUST (4)--->0.28947368421 * (4/37 * 10/36 * 15/35) = 0.00372553004

2.5 + .5 + .5 + .5 + .5 + 4-7 = BUST (4.5)--->0.28947368421 * (10/37 * 9/36 * 8/35 * 7/34 * 15/33) = 0.00041837503

2.5 + .5 + .5 + 1 + 4-7 = BUST (4.5)--->0.28947368421 * (10/37 * 9/36 * 4/35 * 15/34) = 0.00098616971

2.5 + .5 + 1 + .5 + 4-7 = BUST (4.5)--->0.28947368421 * (10/37 * 4/36 * 9/35 * 15/34) = 0.00098616971

2.5 + 1 + .5 + .5 + 4-7 = BUST (4.5)--->0.28947368421 * (4/37 * 10/36 * 9/35 * 15/34) = 0.00098616971

2.5 + 1 + 1 + 4-7 = BUST (4.5) --->0.28947368421 * (4/37 * 3/36 * 15/35) = 0.00111765901

2.5 + 2 + 4-7 = BUST (4.5)--->0.28947368421 * (3/37 * 15/36) = 0.00977951635

Okay, let's add all of these together:

0.06258890469+0.02390548443+0.00614712456+0.00956219377+0.00197233943+0.00372553004+0.00372553004+0.00041837503+0.00098616971+0.00098616971+0.00098616971+0.00111765901+0.00977951635 = 0.12590116648

Stupendous! Now, we just need to add that to the probability that we carried to this section:

0.12590116648 + 0.30367137367 = 0.42957254015 (Dealer Busts)

1 - (0.42957254015) = 0.57042745985 (Dealer Wins)

CONCLUSION

Okay, so the only way that the player wins standing on a 5 against a dealer 2 is if the dealer busts. Unfortunately, the dealer is significantly more likely to complete a playing hand in this scenario because one card that would have been a bust card in the case of DEALER THREE (The other three fives) now makes the dealer a winning hand with a total of 7.

In fact, the probability of the dealer getting the five right off the bat is (3/38) = 0.07894736842

The dealer can also go .5 then 5 for a win, so: (11/38 * 3/37) = 0.02347083926

Therefore, the five switching around results in an overall probability change of 0.02347083926+0.07894736842 = 0.10241820768:

Which impacts both the winning side and the busting side.

The difference between Dealer Wins and Dealer Busts is: 0.57042745985-0.42957254015 = 0.1408549197

In our standing five against Dealer Three, the difference between dealer wins and busts was: 0.51473277788-0.48526722211 = 0.02946555577

Now, if we add to that difference the total new combinations of five causing the dealer to win: 0.10241820768+0.02946555577 = 0.13188376345

Which accounts for almost the entire difference with only: 0.1408549197-0.13188376345 = 0.00897115625 Difference not related to the five directly.

The less than 1% additional difference of the difference between the dealer bust/win rates is likely because it is less likely for the dealer to bust, in general.

One example is the combination 3-1-4 vs. 2-1-4. In the first instance, the dealer would lose. In the second instance, the dealer would win.

It's looking like this might end up being a hitting situation, but we are going to have to look into it to find out.

PLAYER 5 V. DEALER 2--->PLAYER HITS

Okay, so the first thing that we want to do is remember our probabilities of the dealer busting v. the dealer making a hand from our previous analysis:

DEALER BUSTS: 0.42957254015

DEALER WINS: 0.57042745985

Having done that, we will take another look at our deck composition prior to the player hitting:

Remaining Deck:

1-4
2-3
3-4
4-4
5-3
6-4
7-4
J-4
C-4
K3 + WILD

The first thing that can happen is that the player hits and immediately loses. This will take place on any card from 3-7, so:

Player Hits and Loses: (19/38) = .5

Therefore, we start with a 50% chance that the player loses immediately.

The next thing that we will look at is other combinations where the player hits and then takes another card to see if they cause us to exceed the 0.57042745985 probability of the player losing by standing. If this is the case, then we know that the player only wants to take a maximum of one hit.

The most likely scenario is that the player hits a .5 card and then hits a 3-7 card, so let's look at that sequence:

(11/38 * 19/37) = 0.14864864864

If we add that to the .5 that the player busts on the first card, then we know that .64864864864 is the probability of the player busting immediately OR getting a .5 card and then busting. In other words, if the player is going to hit at all, then the player should only hit once.

PLAYER HITS AND DOES NOT BUST

We are going to stick with our most likely scenario of the player hitting and getting a .5, if that happens, the player should certainly stand and our remaining deck composition will be thus:

Remaining Deck:

1-4
2-3
3-4
4-4
5-3
6-4
7-4
J-3
C-4
K3 + WILD

This has an (11/38) chance of even being the case to begin with. If it is the case, then we know the dealer drawing either a four or a five will cause the player to immediately lose.

(11/38) * (7/37) = 0.0547652916

We will combine that with the probability of the player busting: .5 + 0.0547652916 = 0.5547652916

We will remember that the probability of the dealer winning, if the player stands, was 0.57042745985, so we're not terribly far from that. In fact, if we look at the combination:

Player .5, Dealer .5, Dealer 4-5---->The probability may be sufficiently high enough by itself to result in standing and hoping for the dealer to bust being the better decision:

(11/38 * 10/37 * 7/36) = 0.015212581

When we add that to our 0.5547652916 + 0.015212581 = 0.5699778726 it is almost enough that standing is the better decision. What if the player draws a 1 and the dealer then draws a five to beat the player 6-7?

(4/38 * 3/37) = 0.00853485064

We add that to our 0.00853485064 + 0.5699778726 = 0.57851272324 which is more than 0.57042745985 and sufficiently demonstrates that it is better to stand a Player 5 against a Dealer 2.

CONCLUSION

This is a very unfortunate situation for the player, but the least negative decision is to stand with 5 against a dealer 2. We may update our strategy accordingly:

Hitting Decisions:
Player .5 v. Dealer .5 (ANY)---The player can only improve his hand and cannot possibly bust.
Player x v. Dealer x (More than Player)---You must hit.
Player 5 v. Dealer 5---The player doesn't technically have to hit, but the alternative is automatically losing by standing.--So HIT. If the player hits and does not bust, then the player automatically wins, so the player would stand after this.

Standing Decisions:
Player 4 v. Dealer 4---The player should stand as previously demonstrated.
Player 4.5 v. Dealer 4---Because the player should stand on Player 4 v. Dealer 4, it must be true that the player should stand here.
Player 5+ v. Dealer 2---The player should stand.
Player 5+ v. Dealer 3---The player should stand.
Player 5+ v. Dealer 4---The player should stand as previously demonstrated.
Player 5.5+ v. Dealer 5---The player automatically wins and should stand.
Player 5.5+ v. Dealer 4---Because standing on five against a Dealer 4 is true, and this is automatically better (Player wins against Dealer 5) this must be true.
Player 6 v. Dealer (6 or less)---The Player should stand. Just the probability of losing by hitting gives this play a negative expected value.--->The best case scenario for the player to hit is natural six v. natural six (this is the way the fewest cards to bust the player are out) and the player would be 22/38 to bust v. 16/38 (.5-1-W) to win, giving this decision -(6/38) = -0.15789473684 Expected Value compared to the 0 expected value of taking the push. Multi-card instances of Player Six are usually worse because they will generally involve cards that will not bust the player. Technically, the best situation to hit is 2-2-2 v. Dealer 6, but that leaves 36 cards in the deck of which sixteen are winning and twenty are losing.
Player 7 v. Dealer (7 or less)---Obviously, the player should stand.

To Be Determined:

Player 5.5 v. Dealer .5-1

Player 5 v. Dealer .5, 1

Player 4 v. Dealer .5, 1, 2 and 3

Player 3 v. Dealer .5, 1, 2 and 3

Player 2 v. Dealer .5, 1 or 2

Player 1 v. Dealer .5 or 1

PLAYER 5 v. DEALER 1---PLAYER STANDS

If standing on a Player 5 v. Dealer 2 wasn't bad enough (though correct) for the player, things are about to get even worse.

The first thing that we notice about this situation is that a Dealer drawing six (if the player stands) is now winning, where before it was losing. However, this will be somewhat offset (not totally) by the fact that three no longer immediately wins for the dealer. When we combine this with the fact that the player loses all 5-5 pushes, it may be enough to deviate from the strategy where 5-5 is a push, but let's find out.

Remaining Deck Composition:

Remaining Deck:

1-3
2-4
3-4
4-4
5-3
6-4
7-4
J-4
C-4
K3 + WILD

The first thing that happens is that pulling a seven is the only way for the dealer to immediately bust. This will happen on 4/38 = 0.10526315789 of the time.

Dealer Busts Immediately: 0.10526315789

As before, we will look at all of the other ways for the dealer to bust and then add them together. Because ties on five are a loss for the player, anything that is not the dealer busting will cause the player to lose.

Dealer Total 4.5--->Busts with 4-7

The first thing that we are going to look at is all of the different ways for the dealer to get to a 4.5 total and then bust on a 4-7 (15 cards). This will always be fifteen cards because the dealer cannot reach the total if he has drawn a four.

The first way for this to happen is that the dealer gets all half point cards. There is only one possible combination for this:

(11/38 * 10/37 * 9/36 * 8/35 * 7/34 * 6/33 * 5/32 * 15/31) = 0.00001265247

It should be no surprise that this sequence of events is not terribly likely.

The next way is for five half point cards and one one-point card to come out. This can happen six different ways.

(11/38 * 10/37 * 9/36 * 8/35 * 7/34 * 3/33 * 6) = 0.00050205003 * 15/32 = 0.00023533595

The 3/33 represents the one, but you can switch where the three goes with anything else and it won't matter, for instance:

(11/38 * 10/37 * 9/36 * 8/35 * 7/34 * 3/33) = 0.000083675:

Is the same as: (3/38 * 11/37 * 10/36 * 9/35 * 8/34 * 7/33) = 0.000083675:

Which * 6 = 0.000083675*6 = 0.00050205003

The reason for the * 6 is because there are six different positions the one can take in the equation. It will not be the last time we use this concept.

Okay, so the next way we will get to 4.5 is with a two and three-halves.

(11/38 * 10/37 * 9/36 * 4/35 * 4) = 0.00894127209 * 15/34 = 0.00394467886

Again, there are four places in the equation that the two can go.

Next, we will look at 1 + .5 + 3 to get to 4.5 then bust.

(11/38 * 4/37 * 2) = 0.06258890469 * 15/36 = 0.02607871028

You can do it also this way: (11/38 * 4/37) + (4/38 * 11/37) = 0.06258890469--->Same as two places to put the three.

Combinatorics is about to become our best friend. We were effectively doing combinatorics before (determining how many ways something could be expressed), but now we are going to have to do it the short way because we're going to be using more than two numbers. I like this online scientific calculator:

https://web2.0calc.com/

Okay, so 1 + 2 + .5 will also get us to a total of 4.5.

nCr(3,1)*nCr(4,1)*nCr(11,1)/nCr(38,3)= 0.015647226173542 * 15/35 = 0.006705954074375143

"What the hell was that?", you might ask.

Basically, what we did was express every possible way that we can get 3.5 (and, therefore, 4.5 total) out of 2, 1 and .5. Specifically, there are six different ways those numbers can be arranged, which are as follows:

2 + 1 + .5
2 + .5 + 1
1 + 2 + .5
1 + .5 + 2
.5 + 1 + 2
.5 + 2 +1

However, instead of figuring out all six of those individually, or figuring out one of those and multiplying by six, our combinatorial equation did all of them at once. In English our combinatorial equation says this:

If I take three cards from 38 cards that consist of three ones, four twos, eleven half point cards and twenty of everything else combined, what is the probability that I end up with one each of a half point card, a one and a two?

Okay, we can also arrive at 4.5 with two more singles and three half point cards:

nCr(3,2)*nCr(11,3)/nCr(38,5) = 0.0009861697168199 * 15/33 = 0.00044825896219

This is probably a good time to add our probabilities of busting up to a running probability, because we've sure done a lot so far.

0.10526315789+0.00001265247+0.00023533595+0.00394467886+0.02607871028+0.006705954074375143+0.00044825896219= 0.1426887484866

We could also use all of the remaining ones, plus a one half card:

nCr(3,3)*nCr(11,1)/nCr(38,4) = 0.0001490212016528 * 15/34 = 0.00006574465

0.1426887484866+0.00006574465 = 0.1427544931366

Expressed in the simplest way, you can get to 3.5 (by adding to the original one) the following ways starting from the three, which is the biggest number you can add:

3 + .5
2 + 1 + .5
2 + .5 + .5 + .5
1 + 1 + 1 + .5
1 + 1 + .5 + .5 + .5
1 + .5 + .5 +.5 + .5 + .5
.5 * 7

Therefore, there are seven simple ways to do it and, by one means or another, we have covered every possible combination of those ways.

Dealer Total 4--->Busts with 4-7

Our overall probability of the dealer busting right away or busting after a total of 4.5 was 0.1427544931366 so we are going to put that here for safekeeping.

Again, we cannot use a 4-7, or the dealer will have already busted or we will have a total of five+, which would cause the dealer to win. That's kind of good news, because it means that there are still 15 cards that will bust the dealer.

Let's work in reverse this time and look at all of the ways we can arrive at a total of 4, starting from 1:

3
2 + 1
2 + .5 + .5
1 + 1 + 1
1 + 1 + .5 + .5
1 + .5 + .5 + .5 + .5
.5 * 6

Since there is already a nearby example of combinatorics being done, I will let combinatorics do all the work without further explanation:

nCr(4,1)/nCr(38,1) = 0.1052631578947368 * 15/37 = 0.0426742532006

nCr(4,1)*nCr(3,1)/nCr(38,2) = 0.0170697012802276 * 15/36 = 0.0071123755334281667

nCr(4,1)*nCr(11,2)/nCr(38,3) = 0.0260787102892366 * 15/35 = 0.0111765901239585429

nCr(3,3)*nCr(38,3) = 0.0001185395922238 * 15/35 = 0.0000508026823816286

nCr(3,2)*nCr(11,2)/nCr(38,4) = 0.0022353180247917 * 15/34 = 0.0009861697168198676

nCr(3,1)*nCr(11,4)/nCr(38,5) = 0.0019723394336397 * 15/33 = 0.0008965179243816818

nCr(11,6)/nCr(38,6) = 0.0001673500125513 * 15/32 = 0.0000784453183834219

Okay, let's combine all of these and drop a few superfluous decimal places:

0.0426742532006+0.0071123755334281667+0.0111765901239585429+0.0000508026823816286+0.0009861697168198676+0.0008965179243816818+0.0000784453183834219= 0.0629751545

And, combined with our carryover: 0.0629751545 + 0.1427544931366 = 0.2057296476366

Dealer Total 3.5--->Busts with 5-7

Okay, so what we are first going to do is carryover our total 0.2057296476366 probability from before.

The next thing that we realize is that fours are now winning cards for the dealer. As a result, there are only 11 cards (5-7's, one five is ours) that will bust the dealer.

The dealer can get from 1 to 3.5 the following ways:

2 + .5
1 + 1 + .5
1 + .5 + .5 + .5
.5 * 5

As before, the full combinatorics lesson is above, so we're just going to go ahead and bust this out:

nCr(4,1)*nCr(11,1)/nCr(38,2) = 0.0625889046941679 * 11/36 = 0.0191243875454401917

nCr(3,2)*nCr(11,1)/nCr(38,3) = 0.0039118065433855 * 11/35 = 0.0012294249136354429

nCr(3,1)*nCr(11,3)/nCr(38,4) = 0.0067059540743751 * 11/34 = 0.0021695733770037088

nCr(11,5)/nCr(38,5) = 0.0009204250690319 * 11/33 = 0.0003068083563439667

The combined probabilities of these are such: 0.0191243875454401917+0.0012294249136354429+0.0021695733770037088+0.0003068083563439667=0.0228301941924

Added to what we carried over: 0.0228301941924 + 0.2057296476366 = 0.228559841829

Dealer Totals 3---.Busts 5-7

Okay, so the first thing we want to do is remember our carryover probability of 0.228559841829.

The next thing we want to do is determine in what ways the dealer can arrive at a total of 3:

2
1+1
1+.5+.5
5+.5+.5+.5

It remains true that eleven cards bust the dealer.

nCr(4,1)/nCr(38,1) = 0.1052631578947368 * 11/37 = 0.0312944523470839135

nCr(3,2)/nCr(38,2) = 0.0042674253200569 * 11/36 = 0.0013039355144618306

nCr(3,1)*nCr(11,2)/nCr(38,3) = 0.0195590327169275 * 11/35 = 0.0061471245681772143

nCr(11,4)/nCr(38,4) = 0.0044706360495834 * 11/34 = 0.0014463822513358059

Add them together:

0.0014463822513358059+0.0061471245681772143+0.0013039355144618306+0.0312944523470839135 = 0.0401918946811

0.0401918946811+0.228559841829 = 0.2687517365101

Dealer Totals 2.5---.Busts 6-7

Okay, so we have our carryover probability of busting of 0.2687517365101.

Now, we have to see how likely it is the dealer hits to 2.5 and then busts. One problem is that now fives are winning for the dealer, so there are only eight bust cards.

1+.5
.5 + .5 + .5

nCr(3,1)*nCr(11,1)/nCr(38,2) = 0.0469416785206259 * 8/36 = 0.0104314841156946444

nCr(11,3)/nCr(38,3) = 0.0195590327169275 * 8/35 = 0.0044706360495834286

0.0044706360495834286+0.0104314841156946444 = 0.0149021201653

0.0149021201653+0.2687517365101 = 0.2836538566754

Dealer Totals 2---.Busts 6 or 7

Our carryover probability is 0.2836538566754.

There are still eight cards that can bust the dealer.

We can reach a total of two two ways:

1
.5 + .5

nCr(3,1)/nCr(38,1) = 0.0789473684210526 * 8/37 = 0.0170697012802275892

nCr(11,2)/nCr(38,2) = 0.0782361308677098 * 8/36 = 0.0173858068594910667

0.0173858068594910667+0.0170697012802275892 = 0.0344555081397

0.0344555081397 + 0.2836538566754 = 0.3181093648151

Dealer Hits to 1.5---Busts on 7

Carryover Probability: 0.3181093648151

Number of Sevens: 4

Number of 0.5 Cards: 11

Remaining Cards: 38

(11/38 * 4/37) = 0.0312944523470839

0.0312944523470839+0.3181093648151 = 0.3494038171621839

CONCLUSION

If the player stands on 5 against Dealer 1, the probability of the dealer busting is 0.3494038171621839.

If the dealer does not bust, the dealer wins, that probability is 1-0.3494038171621839 = 0.6505961828378161

There's a pretty good chance we have finally hit the time to take a card! Let's find out!

I have to run somewhere, but I'm going to recheck everything above this quote:

Quote: Myself

Expressed in the simplest way, you can get to 4.5 (by adding to the original one) the following ways starting from the three, which is the biggest number you can add:

3 + .5
2 + 1 + .5
2 + .5 + .5 + .5
1 + 1 + 1 + .5
1 + 1 + .5 + .5 + .5
1 + .5 + .5 +.5 + .5 + .5
.5 * 7

Okay, here we go:

nCr(4,1)*nCr(11,1)/nCr(38,2) = 0.0625889046941679 * 15/36 = 0.026078710289236625***

nCr(4,1)*nCr(3,1)*nCr(11,1)/nCr(38,3) = 0.015647226173542 * 15/35 = 0.006705954074375143***

nCr(4,1)*nCr(11,3)/nCr(38,4) = 0.0089412720991668 * 15/34 = 0.0039446788672794706***

nCr(3,3)*nCr(11,1)/nCr(38,4) = 0.0001490212016528 * 15/34 = 0.000065744647788***

nCr(3,2)*nCr(11,3)/nCr(38,5) = 0.0009861697168199 * 15/33 = 0.0004482589621908636***

nCr(3,1)*nCr(11,5)/nCr(38,6) = 0.0005020500376538 * 15/32 = 0.0002353359551502187***

nCr(11,7)/nCr(38,7) = 0.0000261484394611 * 15/31 = 0.0000126524707069839***

0.026078710289236625+0.006705954074375143+0.0039446788672794706+0.000065744647788+0.0004482589621908636+0.0002353359551502187+0.0000126524707069839= 0.0374913352667

The earlier math is confirmed and I have to go again. If you're ever going to send someone to a ******* hardware store when they are trying to work to begin with, make sure you tell them the right item to get and thank you.

PLAYER 5 v. DEALER 1--->PLAYER HITS

Let's first remember our probabilities from before:

If the player stands on 5 against Dealer 1, the probability of the dealer busting is 0.3494038171621839.

If the dealer does not bust, the dealer wins, that probability is 1-0.3494038171621839 = 0.6505961828378161

So, we want a win probability that is better than .3494038171621839.

The first thing that we will look at is the probability that the player busts right away. There are 19 cards (3-7) that will cause this:

19/38 = .5

The next thing that we have to look at is whether or not the player should hit a new total of 5.5. The probability of that happening is (11/38), so, we arrive at:

(11/38 * 19/37) = 0.1486486486486486.

That results in a total probability of .5 + 0.1486486486486486 = 0.6486486486486486 Of Busting out if we hit to 5.5 and then hit again.

Even if we did this and got a .5 (10 left) for 6 or 1 (3 left) for 6.5, the dealer would still instantly win with a six. Let's look at that:

(10/37) + (3/37) = 0.3513513513513514

Follow that with 4/36 for the dealer to get a six and:

0.3513513513513514*(4/36) = 0.0390390390390390444

When we add that to the probability for the player busting by hitting 5 and the probability of the player busting by hitting 5.5 after he has hit five, we get:

0.0390390390390390444+0.6486486486486486 = 0.6876876876876876444

Which is worse than the 0.6505961828378161 probability of losing we would have had just to stand on 5 in the first place.

This means that the player should ONLY take one hit if he is going to hit on five, but let's find out if that is better than standing on 5

Okay, since we know the player should only take one hit, we can determine the probabilities of each player total:

Remaining Deck:

1-3
2-4
3-4
4-4
5-3
6-4
7-4
J-4
C-4
K3 + WILD

Player Bust: 19/38 = .5

Player 7.5 (WILD): 1/38 = 0.0263157894736842

Player 7: 4/38 = 0.1052631579

Player 6: 3/38 = 0.0789473684

Player 5.5: 11/38 = 0.2894736842105263

We're going to need these later.

We're going to start with the most likely one, which is the player gets a .5 card and now has 5.5 against the dealer's 1.

Player 5.5 v. Dealer 1

Player 5.5: 11/38 = 0.2894736842105263

The first thing that we want to do is to determine how the player would beat the dealer in this situation. The first way is for the dealer to end up with any total of exactly five, so let's figure out all the ways that could happen with this remaining deck composition of 37 cards:

Remaining Deck:

1-3
2-4
3-4
4-4
5-3
6-4
7-4
J-3
C-4
K3 + WILD

Those jacks really like to come out.

4
3+1
3+.5+.5
2+2
2+1+1
2+1+.5+.5
2+.5+.5+.5+.5
1+1+1+.5+.5
1+1+.5+.5+.5+.5
1+.5+.5+.5+.5+.5+.5
.5 * 8

nCr(4,1)/nCr(37,1) = 0.1081081081081081 * 0.2894736842105263 = 0.03129445234708392197724039829303

nCr(4,1)*nCr(3,1)/nCr(37,2) = 0.018018018018018 * 0.2894736842105263 = 0.0052157420578473155049786628734

nCr(4,1)*nCr(10,2)/nCr(37,3) = 0.0231660231660232 * 0.2894736842105263 =0.00670595407437513647632595001016

nCr(4,2)/nCr(37,2) = 0.009009009009009 * 0.2894736842105263 = 0.0026078710289236577524893314367

nCr(3,2)*nCr(4,1)/nCr(37,3) = 0.0015444015444015 * 0.2894736842105263 = 0.00044706360495832892298313350945

nCr(3,1)*nCr(4,1)*nCr(10,2)/nCr(37,4) = 0.0081762434703611 * 0.2894736842105263 = 0.00236680732036768671300668204693

nCr(4,1)*nCr(10,4)/nCr(37,5) = 0.0019270607505902 * 0.2894736842105263 = 0.00055783337517084733799377762226

nCr(3,3)*nCr(10,2)/nCr(37,5) = 0.000103235397353 * 0.2894736842105263 = 0.0000298839308127105246857568839

nCr(3,2)*nCr(10,4)/nCr(37,6) = 0.0002709929180517 * 0.2894736842105263 = 0.00007844531838338683782642760971

nCr(3,1)*nCr(10,6)/nCr(37,7) = 0.0000611919492375 * 0.2894736842105263 = 0.00001771345898980263061275869625

nCr(10,8)/nCr(37,8) = 0.0000011655609379 * 0.2894736842105263 = 0.00000033739921886578945528061677

0.03129445234708392197724039829303+0.0052157420578473155049786628734+0.00670595407437513647632595001016+0.0026078710289236577524893314367+0.00044706360495832892298313350945+0.00236680732036768671300668204693+0.00055783337517084733799377762226+0.0000298839308127105246857568839+0.00007844531838338683782642760971+0.00001771345898980263061275869625+0.00000033739921886578945528061677= 0.0493221039161316604676

In other words, the overall probability of this event:

Player 5 v. Dealer 1

Player hits to 5.5, Dealer loses with a total of 5

Is about 0.0493221039161316604676 or 4.93221039161316604676% likely.

Player hits to 5.5, Dealer Busts

The next thing we are going to do is look at the probability of the dealer busting. The good news is that this works pretty close to the same as what we did earlier, with the only exception being the player pulled a 0.5 card out of the deck, which is good for the player, because that card never busts the dealer.

---In other words, all 38's need changed to 37's and all 11's need changed to 10's in the combinatorial formulas. All of our y/x (where y is the number of bust cards available and x is the total number of cards remaining) will become y/(x-1).

DEALER GETS TO 4.5, THEN BUSTS (There are still fifteen bust cards from this spot, 4-7)

3 + .5
2 + 1 + .5
2 + .5 + .5 + .5
1 + 1 + 1 + .5
1 + 1 + .5 + .5 + .5
1 + .5 + .5 +.5 + .5 + .5
.5 * 7

nCr(4,1)*nCr(10,1)/nCr(37,2) = 0.0600600600600601 * 15/35 = 0.0257400257400257571

nCr(4,1)*nCr(3,1)*nCr(10,1)/nCr(37,3) = 0.0154440154440154 * 15/34 = 0.0068135362253009118

nCr(4,1)*nCr(10,3)/nCr(37,4) = 0.0072677719736543 * 15/33 =0.0033035327152974091

nCr(3,3)*nCr(10,1)/nCr(37,4) = 0.0001514119161178 * 15/33 = 0.0000688235982353636

nCr(3,2)*nCr(10,3)/nCr(37,5)= 0.0008258831788244 *15/32 = 0.0003871327400739375

nCr(3,1)*nCr(10,5)/nCr(37,6) = 0.0003251915016621 * 15/31 = 0.0001573507266106935

nCr(10,7)/nCr(37,7) = 0.0000116556093786 * 15/30 = 0.0000058278046893

0.0257400257400257571+0.0068135362253009118+0.0033035327152974091+0.0000688235982353636+0.0003871327400739375+0.0001573507266106935+0.0000058278046893= 0.0364762295502

But, we also must include the fact that the player reached 5.5, so let's do that:

0.2894736842105263 * 0.0364762295502 = .010558908554005262582

Therefore, the total probability of the dealer busting by this event is .010558908554005262582

Combined Probabilities: .010558908554005262582 + 0.0493221039161316604676 = 0.0598810124701369230496

One thing we should have done already is the dealer hits a seven (4/37) and loses immediately, so:

0.0598810124701369230496 + (4/37 * .2894736842105263) = 0.0911754648172208473739243

DEALER HITS TO FOUR, THEN BUSTS

The first thing we will do is carryover our total probability of all of the other ways the dealer can lose:

0.0911754648172208474

We should also keep the probability of the player hitting to 5.5 total in mind, which is: .2894736842105263

There are still fifteen cards that bust the dealer.

3
2 + 1
2 + .5 + .5
1 + 1 + 1
1 + 1 + .5 + .5
1 + .5 + .5 + .5 + .5
.5 * 6

nCr(4,1)/nCr(37,1) = 0.1081081081081081 * 15/36 = 0.0450450450450450417

nCr(4,1)*nCr(3,1)/nCr(37,2) = 0.018018018018018 * 15/35 = 0.007722007722007714

nCr(4,1)*nCr(10,2)/nCr(37,3) = 0.0231660231660232 * 15/34 = 0.0102203043379514118

nCr(3,3)/nCr(37,3) = 0.0001287001287001 * 15/34 = 0.0000567794685441618

nCr(3,2)*nCr(10,2)/nCr(37,4) = 0.0020440608675903 * 15/33 = 0.0009291185761774091

nCr(3,1)*nCr(10,4)/nCr(37,5) = 0.0014452955629426 * 15/32 = 0.0006774822951293437

nCr(10,6)/nCr(37,6) = 0.0000903309726839 * 15/31 = 0.000043708535169629

0.0450450450450450417+0.007722007722007714+0.0102203043379514118+0.0000567794685441618+0.0009291185761774091+0.0006774822951293437+0.000043708535169629 = 0.0646944459800247111 * .2894736842105263 = 0.018727339625797

0.018727339625797+0.0911754648172208474 = 0.1099028044430178474

DEALER HITS TO 3.5, THEN BUSTS

The first thing we will do is carryover our total probability of all of the other ways the dealer can lose:

0.1099028044430178474

We should also keep the probability of the player hitting to 5.5 total in mind, which is: .2894736842105263

There are still eleven cards that bust the dealer, the fours now make a winning hand.

2 + .5
1 + 1 + .5
1 + .5 + .5 + .5
.5 * 5

nCr(4,1)*nCr(10,1)/nCr(37,2) = 0.0600600600600601 * (11/35) = 0.0188760188760188886

nCr(3,2)*nCr(10,1)/nCr(37,3) = 0.0038610038610039 * (11/34) = 0.00124914830797185

nCr(3,1)*nCr(10,3)/nCr(37,4) = 0.0054508289802407 * (11/33) = 0.0018169429934135667

nCr(10,5)/nCr(37,5) = 0.000578118225177 * (11/32) = 0.000198728139904594

0.0188760188760188886+0.00124914830797185+0.0018169429934135667+0.000198728139904594= 0.0221408383173088993*.2894736842105263= 0.006409190039221

0.006409190039221+0.1099028044430178474=0.116311994482239

DEALER HITS TO 3, THEN BUSTS

The first thing we will do is carryover our total probability of all of the other ways the dealer can lose:

0.116311994482239

We should also keep the probability of the player hitting to 5.5 total in mind, which is: .2894736842105263

2
1+1
1+.5+.5
5+.5+.5+.5

It remains true that eleven cards bust the dealer.

nCr(4,1)/nCr(37,1) = 0.1081081081081081 * (11/36) = 0.0330330330330330306

nCr(3,2)/nCr(37,2) = 0.0045045045045045 * (11/35) = 0.0014157014157014143

nCr(3,1)*nCr(10,2)/nCr(37,3) = 0.0173745173745174 * (11/34) =0.0056211673858732765

nCr(10,4)/nCr(37,4) = 0.0031796502384738 * (11/33) = 0.0010598834128246

0.0330330330330330306+0.0014157014157014143+0.0056211673858732765+0.0010598834128246 = 0.0411297852474323214*.2894736842105263 = 0.011905990466362

0.011905990466362+0.116311994482239 = 0.128217984948601

DEALER HITS TO 2.5, THEN BUSTS

The first thing we will do is carryover our total probability of all of the other ways the dealer can lose:

0.128217984948601

We should also keep the probability of the player hitting to 5.5 total in mind, which is: .2894736842105263

Eight Bust Cards (6-7)

1+.5
.5 + .5 + .5

nCr(3,1)*nCr(10,1)/nCr(37,2) = 0.045045045045045 * 8/35 = 0.010296010296010286

nCr(10,3)/nCr(37,3) = 0.0154440154440154 * 8/34 = 0.0036338859868271529

0.0036338859868271529+0.010296010296010286 = 0.0139298962828374389*.2894736842105263 = 0.004032338397663

0.004032338397663+0.128217984948601 = 0.132250323346264

DEALER HITS TO 2, THEN BUSTS

The first thing we will do is carryover our total probability of all of the other ways the dealer can lose:

0.132250323346264

We should also keep the probability of the player hitting to 5.5 total in mind, which is: .2894736842105263

Eight Bust Cards (6-7)

1
.5 + .5

nCr(3,1)/nCr(37,1) = 0.0810810810810811 * 8/36 = 0.0180180180180180222

nCr(10,2)/nCr(37,2) = 0.0675675675675676 * 8/35 = 0.0154440154440154514

0.0180180180180180222+0.0154440154440154514 = 0.0334620334620334736 * .2894736842105263 = 0.0096863781074307

0.0096863781074307+0.132250323346264 = 0.1419367014536947

DEALER HITS TO 1.5, THEN BUSTS

The first thing we will do is carryover our total probability of all of the other ways the dealer can lose:

0.1419367014536947

We should also keep the probability of the player hitting to 5.5 total in mind, which is: .2894736842105263

Four Bust Cards (7's)

(10/37 * 4/36) = 0.03003003003003 * .2894736842105263 = 0.008692903429746

0.008692903429746+0.1419367014536947 = 0.1506296048834407

CONCLUSION ON LOSING

If the player has 5 and hits to 5.5 that has a .2894736842105263 chance of occurring, of that, the dealer will lose over half--0.1506296048834407--of such occurrences. The ways the dealer can lose are by busting immediately, busting after reaching a total below five, or reaching exactly five and losing on score.

PLAYER HITS TO 5.5, DEALER TIES

It is at this point that the dealer tying the player comes into consideration, so we must look at the ways the dealer can start with 1 and reach 5.5:

We should also keep the probability of the player hitting to 5.5 total in mind, which is: .2894736842105263

.5 + 4 (IT MUST BE IN THIS ORDER)
3 + 1 + .5 (THESE CARDS, BUT NOT IN THIS ORDER and NOT 1-3-.5)
2 + 1 + 1 + .5 (ANY ORDER WHERE .5 IS NOT LAST---MULTIPLY BY .75 AFTER)
2 + .5 + .5 + .5 + 1 (ANY ORDER WHERE .5 IS NOT LAST---MULTIPLY BY .4 AFTER)

(10/37) * (4/36) = 0.03003003003003

((nCr(4,1)*nCr(3,1)*nCr(10,1)/nCr(37,3)) - (4/37 * 3/36 * 10/35) - (3/36 * 4/37 * 10/35) = 0.0102960102960103

(nCr(4,1)*nCr(3,2)*nCr(10,1)/nCr(37,4)) * .75 = 0.0013627072450602

(nCr(10,3)*nCr(3,1)*nCr(4,1)/nCr(37,5)) * .4 = 0.001321413086119

Combine these: 0.03003003003003 + 0.0102960102960103 + 0.0013627072450602 + 0.001321413086119 = 0.0430101606572195 * .2894736842105263 = 0.012450309663932

0.012450309663932 is the probability of an eventual tie with the player hitting to 7.5 and staying.

CONCLUSION ON PLAYER 5, HITS TO 5.5, AND DEALER ACTION

Probability of 5.5 Overall: .2894736842105263

Dealer Loses: 0.1506296048834407

Ties: 0.012450309663932

Dealer Wins: .2894736842105263 - 0.1506296048834407 - 0.012450309663932 = 0.1263937696631536

We will also recall that the player has a .5 probability of busting right off the bat, so we add that to the probability of the dealer winning and get:

0.1263937696631536+.5 = 0.6263937696631536

The player is going to have to win a huge many of the 6, 7 and 7.5 situations, otherwise the player is better off just hoping for the dealer to bust. The choice to stand on the five is very likely the best choice, but we'll see. The 5 v. 0.5 situation will definitely be interesting.

Quote: Mission146

Player 7.5 (WILD): 1/38 = 0.0263157894736842

Wow, massively exhaustive analysis, serious props.

One thing that is wrong though is this part. The king of coins is wild in that it can take the role of another card. No card can take a 5 up to 7.5 so the KoC can only replicate a 2, bringing the value to 7.

PLAYER 5 V. DEALER 1, PLAYER HITS TO 6 AND STANDS

Okay, so let's first remember our probabilities from before:

If the player stands on 5 against Dealer 1, the probability of the dealer busting is 0.3494038171621839.

If the dealer does not bust, the dealer wins, that probability is 1-0.3494038171621839 = 0.6505961828378161

So, we want a win probability that is better than .3494038171621839.

------

We have already investigated the Player hitting the 5, receiving a 0.5 value card, then the following results can occur.

Probability of 5.5 Overall: .2894736842105263

Dealer Loses: 0.1506296048834407

Ties: 0.012450309663932

Dealer Wins: 0.1263937696631536

We also can add the probability of .5 that the player busts on his hit to the dealer win rate against 5.5 and get 0.6263937696631536.

Player 6 v. Dealer 1, Dealer Wins

The first thing we should get out of the way is the probability that the player draws to six and the dealer draws a six and wins immediately:

(3/38) * (4/37) = 0.0085348506401138

Okay, so if we add that to the 0.6263937696631536 + 0.0085348506401138 = 0.6349286203032674

The dealer would also win in this scenario by getting the wild card. (3/38 * 1/37) = .0021337126600284

We will carryover a total for the dealer to win of 0.6349286203032674 + .0021337126600284 = 0.6370623329632958

The next thing we will investigate is all of the ways the dealer can get to 7.5, without first hitting anything from 5-7. We have already included the wildcard.

.5 + 6 (In that order)
5 + 1 + .5 (THE FIVE CANNOT BE FIRST OR SECOND---MULTIPLY .33)
5 + .5 + .5 + .5 (THE FIVE CAN ONLY BE LAST---MULTIPLY .25)
4 + 2 + .5 (THE FOUR CANNOT BE FIRST OR SECOND---MULTIPLY .33)
4 + 1 + 1 + .5 (THE FOUR CANNOT BE ANYTHING BUT LAST---MULTIPLY .25)
4 + .5 + .5 + .5 + .5 + .5 (THE FOUR MUST BE LAST---MULTIPLY .167)
3 + 3 + .5 (ONE OF THE THREES MUST BE LAST---MULTIPLY .66)
3 + 2 + 1 + .5 (THE THREE MUST BE LAST---MULTIPLY .25)

(11/37) * (4/36) = 0.033033033033033
(nCr(3,1)*nCr(2,1)*nCr(11,1)/nCr(37,3)) * .33 = 0.0028030888030888
(nCr(3,1)*nCr(11,3)/nCr(37,4)) * .25 = 0.0018737224619578
(nCr(4,1)*nCr(4,1)*nCr(11,1)/nCr(37,3))*.33 = 0.0074749034749035
(nCr(2,2)*nCr(11,1)*nCr(4,1)/nCr(37,4)) * .25 = 0.0001665531077296
(nCr(4,1)*nCr(11,5)/nCr(37,6)) * .167 = 0.0001327503974563
(nCr(4,2)*nCr(11,1)/nCr(37,3)) * .66 = 0.0056061776061776
(nCr(4,1)*nCr(4,1)*nCr(11,1)*nCr(2,1)/nCr(37,4)) * .25 = 0.0013324248618366

0.033033033033033+0.0028030888030888+0.0018737224619578+0.0074749034749035+0.0001665531077296+0.0001327503974563+0.0056061776061776+0.0013324248618366=0.0524226537461832 * (3/38) = 0.0041386305589092

Okay, so the probability that the player will draw a 1 to a total of six but get beaten by the dealer with a total of 7.5 is 0.0041386305589092 (We had already included the wildcard)

0.0041386305589092+0.6370623329632958 = 0.641200963522205

We're less than 1% away now. The next scenario is going to be that the dealer wins with a total of seven, though we have already included the dealer getting the six outright, so let's come up with all other possibilities to get to 7 without hitting 5-6.5 first:

6 (Already Included)
5 + 1 (Opposite Order)*
5 + .5 + .5 (THE FIVE MUST BE LAST---MULTIPLY .33)*
4 + 2 (OPPOSITE ORDER)*
4 + 1 + 1 (THE FOUR MUST BE LAST---MULTIPLY .33)*
4 + 1 + .5 + .5 (THE FOUR MUST BE LAST---MULTIPLY .25)*
4 + .5 + .5 + .5 + .5 (THE FOUR MUST BE LAST---MULTIPLY .2)*
3 + 3*
3 + 2 + 1 (THE THREE MUST BE LAST---MULTIPLY .33)*
3 + 2 + .5 + .5 (THE THREE MUST BE LAST---MULTIPLY .25)*
3 + 1 + 1 + .5 + .5 (THE THREE MUST BE LAST---MULTIPLY .2)*
3 + 1 + .5 + .5 + .5 + .5 (THE THREE MUST BE LAST---MULTIPLY .167)*
----ANYTHING INCLUDING ALL LOWER THAN TWO IS NOT POSSIBLE

(11/37 * 3/36) = 0.0247747747747748
(nCr(3,1)*nCr(11,2)/nCr(37,3)) * .33 = 0.007007722007722
(4/37 * 4/36) = 0.012012012012012
(nCr(2,2)*nCr(4,1)/nCr(37,3)) * .33 = 0.0001698841698842
(nCr(4,1)*nCr(11,2)*nCr(2,1)/nCr(37,4)) * .25 = 0.0016655310772958
(nCr(4,1)*nCr(11,4)/nCr(37,5)) * .2 = 0.0006056476644712
nCr(4,2)/nCr(37,2) = 0.009009009009009
(nCr(4,1)*nCr(4,1)*nCr(2,1)/nCr(37,3)) * .33 = 0.0013590733590734
(nCr(4,1)*nCr(4,1)*nCr(11,2)/nCr(37,4)) * .25 = 0.0033310621545916
(nCr(4,1)*nCr(2,2)*nCr(11,2)/nCr(37,5)) * .2 = 0.0001009412774119
(nCr(4,1)*nCr(2,1)*nCr(11,4)/nCr(37,6)) * .167 = 0.0001896434249375

0.0247747747747748+0.007007722007722+0.012012012012012+0.0001698841698842+0.0016655310772958+0.0006056476644712+0.009009009009009+0.0013590733590734+0.0033310621545916+0.0001009412774119+0.0001896434249375= 0.0602253009311834*(3/38) = 0.0047546290208829

Okay, we had already included the straight up six, so ways that other ways that the dealer could beat the player 6-7 total 0.0047546290208829:

0.0047546290208829 + 0.641200963522205 = 0.6459555925430879--->We are still a little short of our target of .6506

Next thing we have to do is look at the probability of the dealer winning with a total of 6.5 without transgressing into 5-6 territory. That's going to be a fairly reasonable demand, so let's look at the ways it can happen:

5 + .5 (Opposite order)*
4 + 1 + .5 (THE FOUR MUST BE LAST---MULTIPLY .33)*
4 + .5 + .5 + .5 (THE FOUR MUST BE LAST---MULTIPLY .25)*
3 + 2 + .5 (THE THREE MUST BE LAST---MULTIPLY .33) or the specific order .5-3-2 also works)*
3 + 1 + 1 + .5 (THE THREE MUST BE LAST---MULTIPLY .25)*
3 + 1 + .5 + .5 + .5 (THE THREE MUST BE LAST---MULTIPLY .2)*
3 + .5 + .5 + .5 + .5 + .5 (THE THREE MUST BE LAST---MULTIPLY .167)*
2-2-1-.5 (ONE OF THE TWOS MUST BE LAST---MULTIPLY .5)*
2-2-.5-.5-.5 (ONE OF THE TWOS MUST BE LAST---MULTIPLY .4)*
2-1-.5-.5-.5-.5-.5 (THE TWO MUST BE LAST---MULTIPLY .14286)*
2-.5-.5-.5-.5-.5-.5-.5 (THE TWO MUST BE LAST---MULTIPLY .125)*

(11/37*3/36) = 0.0247747747747748
(nCr(4,1)*nCr(2,1)*nCr(11,1)/nCr(37,3)) * .33 = 0.0037374517374517
(nCr(4,1)*nCr(11,3)/nCr(37,4)) * .25 = 0.0024982966159437
(nCr(4,1)*nCr(4,1)*nCr(11,1)/nCr(37,3)) * .33 = 0.0074749034749035 + (11/37 * 4/36 * 4/35) = 0.0112501072501072752
(nCr(4,1)*nCr(11,1)*nCr(2,2)/nCr(37,4)) * .25 = 0.0001665531077296
(nCr(2,1)*nCr(4,1)*nCr(11,3)/nCr(37,5)) * .2 = 0.0006056476644712
(nCr(4,1)*nCr(11,5)/nCr(37,6)) * .167 = 0.0001327503974563
(nCr(4,2)*nCr(2,1)*nCr(11,1)/nCr(37,4)) * .25 = 0.0004996593231887
(nCr(4,2)*nCr(11,3)/nCr(37,5)) * .4 = 0.0009084714967068
(nCr(4,1)*nCr(2,1)*nCr(11,5)/nCr(37,7)) * .14286 = 0.0000512857069593
(nCr(4,1)*nCr(11,7)/nCr(37,8)) * .125 = 0.0000042737234388


0.0247747747747748+0.0037374517374517+0.0024982966159437+0.0112501072501072752+0.0001665531077296+0.0006056476644712+0.0004996593231887+0.0009084714967068+0.0000512857069593+0.0000042737234388 = 0.044496521400772 * 3/38 = 0.003512883268482

0.003512883268482 + 0.6459555925430879 = 0.6494684758115692--->Getting pretty close to .6506

Okay, now the dealer can actually tie on 6, of course. However, he cannot have a score of 5 or 5.5 if he does. Let's look at all of the ways this can happen:

5 (3/37) = 0.0810810810810811*
4 + 1 (Opposite Order)*
4 + .5 + .5 (THE FOUR MUST BE LAST---MULTIPLY .333)*
3 + 2 (Any Order)*
3 + 1 + 1 (THE THREE MUST BE LAST---MULTIPLY BY .333)*
3 + 1 + .5 + .5 (THE THREE MUST BE LAST---MULTIPLY BY .25)*
3 + .5 + .5 + .5 + .5 (THE THREE MUST BE LAST---MULTIPLY BY .2)*
2 + 2 + 1 (ONE OF THE TWOS MUST BE LAST---MULTIPLY .666)*
2 + .5 + .5 + 2 (THIS ORDER ONLY)*

0.0810810810810811
(11/37*4/36) = 0.033033033033033
(nCr(4,1)*nCr(11,2)/nCr(37,3)) * .333 = 0.0094285714285714
nCr(4,1)*nCr(4,1)/nCr(37,2) = 0.024024024024024
nCr(4,1)*nCr(11,2)/nCr(37,3) * .333 = 0.0094285714285714
(nCr(4,1)*nCr(2,1)*nCr(11,2)/nCr(37,4)) * .25 = 0.0016655310772958
(nCr(4,1)*nCr(11,4)/nCr(37,5)) * .2 = 0.0006056476644712
(nCr(4,2)*nCr(2,1)/nCr(37,3)) * .666 = 0.0010285714285714
(4/37 * 11/36 * 11/35 * 3/34) = 0.0009160420925127 * 2 (THE TWOS CAN APPEAR IN EITHER PLACE) = 0.0018320841850254


0.0810810810810811+0.033033033033033+0.0094285714285714+0.024024024024024+0.0094285714285714+0.0016655310772958+0.0006056476644712+0.0010285714285714+0.0018320841850254 = 0.1621271153506447 * 3/38 = 0.0127995091066298447

Okay, so the overall probability of the player hitting to 6 is 3/38 = 0.0789473684210526

The player will lose 0.0085348506401138 + 0.0041386305589092 + 0.0047546290208829 + 0.003512883268482 + .0021337126600284 = 0.0230747061484163

The player and dealer will tie: 0.0127995091066298447

Therefore, the player's win rate goes up by 0.0789473684210526 - 0.0230747061484163 - 0.0127995091066298447 = 0.0430731531660064553

We have already investigated the Player hitting the 5, receiving a 0.5 value card, then the following results can occur.

Here are our results from the 5.5 scenario:

Dealer Loses: 0.1506296048834407

Ties: 0.012450309663932

Dealer Wins: 0.1263937696631536

So, now we add our sixes scenarios:

Dealer Loses: 0.1506296048834407 + 0.0430731531660064553 = 0.1937027580494471553

Ties: 0.012450309663932 + 0.0127995091066298447 = 0.0252498187705618447

Dealer Wins: .5 + 0.1263937696631536 + 0.0230747061484163 = 0.6494684758115699

Running Expected Value:

(0.1937027580494471553) + (0.0252498187705618447 * 0) - (0.6494684758115699) = -0.4557657177621227447

Expected Value of Standing on 5:

If the player stands on 5 against Dealer 1, the probability of the dealer busting is 0.3494038171621839

If the dealer does not bust, the dealer wins, that probability is 1-0.3494038171621839 = 0.6505961828378161

0.3494038171621839-0.6505961828378161 = -0.3011923656756322

It's official, STANDING on 5 against a dealer 1 is the superior decision. Another way to prove it is that we know the probability of the player hitting and receiving the WILD or a three to make 7 is a combined (5/38) = 0.1315789473684211

So, let's take our other probabilities that we have determined and see how this adds up:

0.1315789473684211 + 0.1937027580494471553 + 0.0252498187705618447 + 0.6494684758115699 = 1

Therefore, we have now encompassed every single possibility.

Just for giggles, let's assume that the player ALWAYS wins on 7 and 7.5, never loses:

Dealer Loses: 0.1506296048834407 + 0.0430731531660064553 = 0.1937027580494471553 + 0.1315789473684211 = 0.3252817054178682553

Ties: 0.012450309663932 + 0.0127995091066298447 = 0.0252498187705618447

Dealer Wins: .5 + 0.1263937696631536 + 0.0230747061484163 = 0.6494684758115699

EV: 0.3252817054178682553 + (0.0252498187705618447*0) - (0.6494684758115699) = -0.3241867703937016447

Therefore, even if the player could ONLY win on totals of 7 and 7.5, it would still be a worse decision than just standing the Player 5 v. Dealer 1 and hoping for the dealer to bust.

CONCLUSION

The player should stand with a 5 against a dealer 1, but it's a reasonably close call. Because this is true, it is also true that the player should stand 5.5 against a dealer 1.

Let's update our chart:

Hitting Decisions:
Player .5 v. Dealer .5 (ANY)---The player can only improve his hand and cannot possibly bust.
Player x v. Dealer x (More than Player)---You must hit.
Player 5 v. Dealer 5---The player doesn't technically have to hit, but the alternative is automatically losing by standing.--So HIT. If the player hits and does not bust, then the player automatically wins, so the player would stand after this.

Standing Decisions:
Player 4 v. Dealer 4---The player should stand as previously demonstrated.
Player 4.5 v. Dealer 4---Because the player should stand on Player 4 v. Dealer 4, it must be true that the player should stand here.
Player 5+ v. Dealer 1
Player 5+ v. Dealer 2---The player should stand.
Player 5+ v. Dealer 3---The player should stand.
Player 5+ v. Dealer 4---The player should stand as previously demonstrated.
Player 5.5+ v. Dealer 5---The player automatically wins and should stand.
Player 5.5+ v. Dealer 4---Because standing on five against a Dealer 4 is true, and this is automatically better (Player wins against Dealer 5) this must be true.
Player 6 v. Dealer (6 or less)---The Player should stand. Just the probability of losing by hitting gives this play a negative expected value.--->The best case scenario for the player to hit is natural six v. natural six (this is the way the fewest cards to bust the player are out) and the player would be 22/38 to bust v. 16/38 (.5-1-W) to win, giving this decision -(6/38) = -0.15789473684 Expected Value compared to the 0 expected value of taking the push. Multi-card instances of Player Six are usually worse because they will generally involve cards that will not bust the player. Technically, the best situation to hit is 2-2-2 v. Dealer 6, but that leaves 36 cards in the deck of which sixteen are winning and twenty are losing.
Player 7 v. Dealer (7 or less)---Obviously, the player should stand.

To Be Determined:

Player 5.5 v. Dealer .5

Player 5 v. Dealer .5

Player 4 v. Dealer .5, 1, 2 and 3

Player 3 v. Dealer .5, 1, 2 and 3

Player 2 v. Dealer .5, 1 or 2

Player 1 v. Dealer .5 or 1

Quote: rumba434

Wow, massively exhaustive analysis, serious props.

One thing that is wrong though is this part. The king of coins is wild in that it can take the role of another card. No card can take a 5 up to 7.5 so the KoC can only replicate a 2, bringing the value to 7.

Thanks for the compliment!

Thanks for pointing that out! I'll keep it in mind for the future, but to this point, it wouldn't have changed any of our decisions. In fact, there hasn't been a single decision point yet to favor hitting unless you have to.

Tomorrow, we're going to look at these situations:

Player 5.5 v. Dealer .5

Player 5 v. Dealer .5

Player 4 v. Dealer .5, 1, 2 and 3

Player 3 v. Dealer .5, 1, 2 and 3

Player 2 v. Dealer .5, 1 or 2

Player 1 v. Dealer .5 or 1

I've got to say that Player 5 v. Dealer 1 was so close to being a hit that I expect Player 5 v. Dealer .5 to be a hit, but we'll find out. The main reason I expect for this to be the case is because the dealer cannot bust on his first card, so that gives him many more opportunities of making a hand of 5+.

Even when the dealer only had 1, his probability of hitting and busting instantly was 4/38 = 0.1052631578947368

And, when we look at the fact that card was the seven when the dealer was hitting to one, we realize that a seven hitting to .5 would cause the dealer to instantly win.

While it is true that a 4 is no longer an instant win for the dealer hitting .5 against a Player 5, the four doesn't bust him, either. It brings his total to 4.5, at which point, the dealer will have 23/37 cards that make a hand and 14/37 (4-7---one four and one five have been taken) that will bust him.

So, where a seven would have automatically busted the dealer with 0.1052631578947368 probability it wins and the four no longer automatically wins. However, if the player is standing, the four effectively wins:

23/37 = 0.6216216216216216

Loses

14/37 = 0.3783783783783784

Difference = (0.6216216216216216-0.3783783783783784) * 4/38 = 0.025604551920

Therefore, I believe the probability of the dealer making a hand of 5+ improves overall by approximately that percentage*, which would be 2.5604552%.

That means that you can add that to the player's loss rate, as the dealer making any hand against a standing 5 is an automatic loss for the player.

*Does not consider other potential effects-of-removal, this is just what immediately changes.

Actually...

I actually had a dream about all of these numbers last night, and when I woke up, something pretty simple occurred to me: If the player has less than five points, hitting is worse for the player than in this version:

https://wizardofodds.com/games/siete-y-media/

The reason why, quite simply, is because the player loses on ties of five, aside from that, it would be the same exact expected value. Losses on ties of five, however, cause the expected value of the decision to be worse.

In other words, anything with the player having a five (or less) that would be a stand on Siete y Media would also be a stand on this game AND the stand would become a better decision.

Player 4: Player Stands on Anything

Player 3.5: Player Stands against 2 and 3.

Player 3: Player stands against 1 & 2

----

There are a few borderline hits that we will have to look at since the possibility of tying makes hitting slightly worse.

Player 4.5 v. .5 or 1 (This will be interesting. It's a hit in Siete y Media, but getting a .5 card does nothing for the player in this version)

Player 3.5 v. .5 or 1 (This is a hit in Siete y Media, and I don't expect that to change. The player cannot possibly end up with a total of 5 and .5 for 4 becomes a stand)

Player 3 v. Dealer .5 (This is a hit in Siete y Media, so It'll really depend how close of a decision it is.)

Player 2.5 v. .5-2 (These are hits and no reason for that to change. The player cannot get to 5 with one card, and even if hitting twice and getting to five, takes low cards from the dealer---but we'll see.)

Player 2 v. Dealer .5, 1 (This might change because getting to a total of five doesn't do the player any favors.)

Player 1.5 v. Dealer .5-1 (I can't imagine this changing)

Player 1 v. Dealer .5 or 1 (I can't imagine this changing)

Aside from that, we still have to see if:

Player 5 v. Dealer .5

Is a hit or a stand in this version.

-------

Okay, so we can update our list a little bit:

Hitting Decisions:
Player .5 v. Dealer .5 (ANY)---The player can only improve his hand and cannot possibly bust.
Player x v. Dealer x (More than Player)---You must hit.
Player 5 v. Dealer 5---The player doesn't technically have to hit, but the alternative is automatically losing by standing.--So HIT. If the player hits and does not bust, then the player automatically wins, so the player would stand after this.

Standing Decisions:
Player 3---Stand against Dealer 1 or 2
Player 3.5---Stand against Dealer 2 or 3
Player 4 v. Dealer 4 or ANY LOWER---The player always stands on four.
Player 4.5 v. Dealer 4 or LOWER---Because the player should stand on four it must be true the player stands here.
Player 5+ v. Dealer 1-4---The player should stand.
Player 5.5+ v. Dealer ANY LOWER CARD---Always stand on 5.5.
Player 6 v. Dealer ANY LOWER CARD---Always stand on 6.
Player 7 v. Dealer (7 or less)---Obviously, the player should stand.

Quote: Mission146

Actually...

I actually had a dream about all of these numbers last night, and when I woke up, something pretty simple occurred to me: If the player has less than five points, hitting is worse for the player than in this version:

/games/siete-y-media/

Not that I want to force you into more work, as what you've done so far is truly awesome, but is that definitely true? The presence of the king of coins is an incentive to hit that may outweigh the disincentive that ties on 5 go to dealer creates.

Anecdotally from playing it, the KoC swooping in to save a bad hand happens a lot lot more than any worries about tying on 5.

Quote: rumba434

Quote: Mission146

Actually...

I actually had a dream about all of these numbers last night, and when I woke up, something pretty simple occurred to me: If the player has less than five points, hitting is worse for the player than in this version:

/games/siete-y-media/

Not that I want to force you into more work, as what you've done so far is truly awesome, but is that definitely true? The presence of the king of coins is an incentive to hit that may outweigh the disincentive that ties on 5 go to dealer creates.

Anecdotally from playing it, the KoC swooping in to save a bad hand happens a lot lot more than any worries about tying on 5.

Damn, that’s a good point. I just read it again and there is no wild in Wizard’s game.

With that said, though, there are generally going to be more cards (hitting with less than five from a solid number or 4.5) that cause the player to get to 5 rather than getting the wild. We’ll have to look into it, but 4.5 is almost certainly a stand. The .5 cards are very likely and do nothing for you.

Mission, I admire your hard work on this game. The version I saw in Uruguay didn't have a wild card. For purposes of analyzing games, I hate wild cards. However, this one will not be so bad. I have a lot of balls in the air right now, but maybe I'll try to analyze this Playtech version later. I will probably start with a spreadsheet to determine an infinite-deck strategy and then run it through a simulation.

Can anyone quote a source to verify the rules in the OP are correct?

Quote: Wizard

Mission, I admire your hard work on this game. The version I saw in Uruguay didn't have a wild card. For purposes of analyzing games, I hate wild cards. However, this one will not be so bad. I have a lot of balls in the air right now, but maybe I'll try to analyze this Playtech version later. I will probably start with a spreadsheet to determine an infinite-deck strategy and then run it through a simulation.

Can anyone quote a source to verify the rules in the OP are correct?

There are multiple YouTube videos of the game actually in action, the stated rules are correct.

Quote: Wizard

Mission, I admire your hard work on this game. The version I saw in Uruguay didn't have a wild card. For purposes of analyzing games, I hate wild cards. However, this one will not be so bad. I have a lot of balls in the air right now, but maybe I'll try to analyze this Playtech version later. I will probably start with a spreadsheet to determine an infinite-deck strategy and then run it through a simulation.

Can anyone quote a source to verify the rules in the OP are correct?

I can't copy the text from the Playtech help file, otherwise I'd quote it.

I checked the Playtech rules and it doesn't say that the dealer takes a second card when KoC is his first card, but I've just played and eventually got a hand where KoC was 1st dealer card and player didn't bust trying to get to 7. The dealer DOES take a second card if his first card is KoC

If the 1st 2 cards are the KoC and 7/0.5 it is a "Royal Sette e Mezzo", which beats 7.5 and pays 3:2 if the player gets it.

Would this wording of the rules be accurate (version 2):

1. The game uses a single custom 40-card deck. The deck consists of ten ranks and four suits.
2. The ten ranks are 1 to 7, jacks, cavaliers, and kings. Ranks of 1 to 7 are worth face value. All others (face cards) are worth 0.5 points.
3. The four suits are swords, cups, coins, and clubs. Suits are irrelevant, except for the king of coins.
4. The king of coins may be worth the value of any other card.
5. Play starts with the player and dealer each receiving one card face up.
6. If the player's card is less than the dealer's card in value, then the player is obligated to hit until he has at least as many points as the dealer.
7. If the player has equal or more points than the dealer, he has free will to hit or stand.
8. If the player goes over 7.5 points, then he automatically loses.
9. The dealer shall hit with 4.5 points or less and stand with 5 points or more. He will also take exactly 1 card if his first card was the king of coins.
10. The highest ranking hand is a "Royal 7.5," which consists of two cards totaling 7.5 including the King of Coins. This can be achieved only if the other card is 0.5 or 7 points. A Royal hand shall outrank all other hands and pay 3 to 2.
11. If the dealer goes over 7.5 points, any player hands still standing shall win.
12. Otherwise, if the player has more points than the dealer, the player shall win.
13. Otherwise, if the dealer has more points than the player, the dealer shall win.
14. Otherwise, if the player and dealer tie with five points each, the player shall lose.
15. Otherwise, any other tie, is a push.

There are a couple of side bets, pictured here:



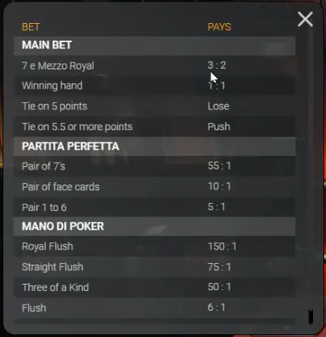
Live Casino Comparer has a video on the game. He covers the "royal" hand 3-2 pay starting about 3:55.

Quote: Wizard

Would this wording of the rules be accurate:

1. The king of coins may be worth any whole number from 1 to 7 or 0.5.
2. The dealer shall hit with 4.5 points or less and stand with 5 points or more. He will also take exactly 1 card if his first card was the king of coins
3. All wins pay even money, except a "Royal" hand win shall pay 3 to 2. A Royal hand consists of the the King of Coins and half-point card or 7 point card. A Royal hand beats a standard 7.5

I have made some adjustments to 3 of your points which you may wish to reword or reorder.

Also 12 and 13 are repeats of each other, one of them should reverse the words "player" and "dealer"

That picture is missing 5:1 for a straight. Playtech do not explain this anywhere so I had to ask the dealer, (in English which annoyed her!): 7-J-C and C-K-A are not straights.

Note you only qualify for the Mano di poker bet if you take your second card, so if you had say a 6 of cups and the dealer a 5 of cups you're basically sacrificing a won hand for a hand with a good chance of busting to try to win the sidebet.

Quote: rumba434

I have made some adjustments to 3 of your points which you may wish to reword or reorder.

Also 12 and 13 are repeats of each other, one of them should reverse the words "player" and "dealer"

Thank you. I just made those changes. Not to doubt you, but can you quote any source that a Royal hand outranks an otherwise 7.5-point hand? If I get challenged, it would be nice to have something more firm to quote than a forum post.

I also thank you for the comment on the straight.

Quote: Wizard

Thank you. I just made those changes. Not to doubt you, but can you quote any source that a Royal hand outranks an otherwise 7.5-point hand? If I get challenged, it would be nice to have something more firm to quote than a forum post.

I also thank you for the comment on the straight.

Point 10 still doesn't include KoC/7 as a "Royal Sette e Mezzo"
It also doesn't explain what happens if the dealer's hand is higher than the player, (which people would obviously infer, but just pointing out for completeness)

I can't copy text from Playtech's help but will transcribe the relevant line

"King of coins can also form the Sette e Mezzo royal, a special combination with two cards (King of Coins and another face card or a 7), which totals 7.5 points and wins over the regular 7.5-value hand"

Quote: rumba434

Point 10 still doesn't include KoC/7 as a "Royal Sette e Mezzo"
It also doesn't explain what happens if the dealer's hand is higher than the player, (which people would obviously infer, but just pointing out for completeness)

I can't copy text from Playtech's help but will transcribe the relevant line

"King of coins can also form the Sette e Mezzo royal, a special combination with two cards (King of Coins and another face card or a 7), which totals 7.5 points and wins over the regular 7.5-value hand"

Thank you. I think it would confuse the reader if I said a Royal Sette e Mezzo beats a "higher" dealer hand, because there is no hand higher than 7.5. It should be addressed what happens if the player a Royal Sette e Mezzo and the dealer has 7.5 points, which I think I do address.

If possible, can you give me a screenshot of the Playtech rules, even if in Italian.

Quote: Wizard

Thank you. I think it would confuse the reader if I said a Royal Sette e Mezzo beats a "higher" dealer hand, because there is no hand higher than 7.5. It should be addressed what happens if the player a Royal Sette e Mezzo and the dealer has 7.5 points, which I think I do address.

If possible, can you give me a screenshot of the Playtech rules, even if in Italian.

Point 10 still hasn't been updated to include KoC and 7

What I meant by the other part was that rules 11-14 list every scenario except "dealer has higher score than player". Unless you're an idiot you can make the inference that the dealer wins but it's not explicit.

I can't see a way to upload images and even if I did Playtech divide it into so many disparate sections that you can't full screen it would take about 10 images.

Quote: rumba434

Point 10 still hasn't been updated to include KoC and 7

Ah, thanks.

Note to myself: Rules from livecasinocomparer.com.

If the dealer has the King of Cups showing, I assume the player will hit to 7 or 7.5. Then, I assume the dealer will take just one more card -- giving him a 7 or royal 7.5, depending on the second card.

Assuming the above strategy adjustments from the strategy in my Siete y Media page (below), I'm getting a house edge of 0.45%. I plan to apply adjustments to the strategy to see if it helps.

I now see some of the plays in the Siete y Media strategy above are not allowed in it Playtech game. It may have just been a coincidence my figure was in the reasonable range. At this point, I'm going to not throw out a number until I'm more confident in it.

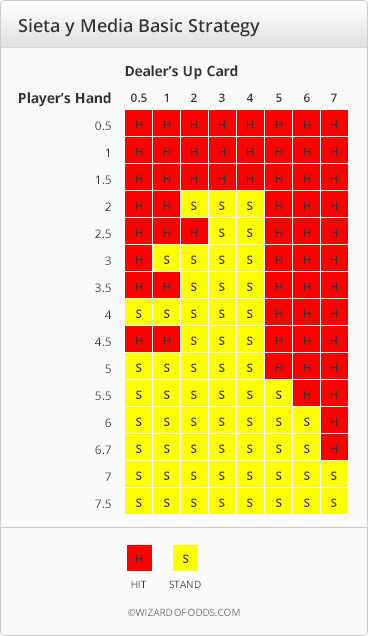
Quote: Wizard

I saw this game in Uruguay. Here is my page on Siete y Media (seven and a half).

Wiz,

You have a typo on your strategy table: "6.7" should be "6.5".

Dog Hand

Here's my guestimate - please note I have not checked this with a simulation.
Assumptions
There are no special hands such as making 7.5 with your first two cards.
Dealer hits Joker with one card only.
Dealer stands on all other totals of 5 or more and hits all totals 4.5 or less.
This is a single deck game.
Special Rules
Dealer wins any 5-5 ties.
Player "must hit" any total which is less than the dealer (the most effect is having to hit vs dealer 4).

Infinite Deck where player must hit	2.261%
Infinite Deck where player may stand	1.824%
Single Deck where player must hit	1.533%
Single Deck where player may stand	0.920%

(The losing Ties 5-5 rule costs the player about 1.3%.)
Single Deck Strategy

	Dealer's	Dealer's	Dealer's	Dealer's	Dealer's	Dealer's	Dealer's	Dealer's
	UpCard	UpCard	UpCard	UpCard	UpCard	UpCard	UpCard	UpCard
Player's Hand	Picture	Ace	2	3	4	5	6	7
0.5	H	H	H	H	H	H	H	H
1	H	H	H	H	H	H	H	H
1.5	H	H	H	H	H	H	H	H
2	H	H	H	H	Must	H	H	H
2.5	H	H	H	H **	Must	H	H	H
3	H	st	st	st	Must	H	H	H
3.5	H	H	st	st	Must	H	H	H
4	St *	st	st	st	st	H	H	H
4.5	H	st	st	st	st	H	H	H
5	St *	st	st	st	st	H	H	H
5.5	st	st	st	st	st	st	H	H
6	st	st	st	st	st	st	st	H
6.5	st	st	st	st	st	st	st	H
7	st	st	st	st	st	st	st	st

Note:
* Hit singletons 5 or 4 versus dealer's Picture card.
** Some hands wouldn't hit if there had been an option.
Always hit singleton Joker.
Treat Dealer's Joker as if it was a Seven.

Nice! I knew 5 v 0.5 would be a hit, but I stopped working on it when I saw Wizard would ultimately run a full simulation.

Thanks CharliePatrick!

Good work Charlie!

I was going to post my results of a simulation using the Siete y Media strategy, except where a hit was forced. That got a house edge of 1.59%.

When I ran your strategy, I get the following results.

Event	Pays	Simulation	Probability	Return
Total player royals=	1.5	8,729,752	0.016660	0.024990
Total dealer royals=	-1	8,728,561	0.016658	-0.016658
Total player win=	1	114,551,182	0.218609	0.218609
Total dealer win=	-1	110,919,521	0.211678	-0.211678
Total player bust=	-1	118,220,293	0.225611	-0.225611
Total dealer bust=	1	113,000,323	0.215649	0.215649
Total 5-5 tie=	-1	6,694,572	0.012776	-0.012776
Total other tie=	0	43,155,796	0.082358	0.000000
Total		524,000,000	1.000000	-0.007475

In other words, a house edge of 0.75%. I see this is half your 1.5% house edge. Is it possible you were betting 2 units at a time, to keep wins and losses in integers, and forgot to divide by 2 (a mistake I've made before)?

^ You'll see under my assumptions there are no special hands as I didn't read anything about "Royals" paying 3:2. However I can add that and see what I get. (Using your figures the contribution would be about the difference.)

Adding Royals - the code presumed the Dealer could Tie if they started with a Joker and drew a Royal or immediately draw a Joker to a Picture - although that's not possible for this single deck game as I've made it general case logic! I'm assuming this also works the other way round that a Dealer's Royal will beat other totals of 7.5.

If the player has to hit - House Edge = 0.725%
If the player doesn't have to hit - House Edge = 0.111%

Thanks for considering where we may have had different rules. I should have read your assumptions more carefully. I endeavor to only analyze the Playtech rules at this time. I treat a Royal like a blackjack, where it outranks all other hands, and pays more if the dealer has it. Since there is only only King of Coins in the deck, I didn't have to wonder about what happens in a Royal tie.

I think I'm ready to write this up.

Thanks again Charlie. You will certainly get an acknowledgement for your help.

Here is a link to the help/info page of another version of this game (see below)
https://www.lottomatica.it/aiuto/casino/sette-e-mezzo

Key Points or Differences:

"The king of denari (diamonds) is the fool and can take any of the following values ​​chosen by the player who owns it: ½, 1, 2, 3, 4, 5, 6, 7..." , so in other words, instead of the king of coins, the king of denari is the wild card

"With the same score, the player simply withdraws his initial stake" ***, in other words, push on 5 and above when you tie with the dealer (IMPORTANT: including 5 vs 5)

***: Through testing I can confirm that a tie on 5 vs 5 results in getting your bet returned.

Doesn't appear to have any "bonus payouts" (eg all wins are 1/1)

According to the info page link above, the RTP is 99.8274% (when you play "best strategy")


Note: Except for where I have written "bonus payouts" above and "google translate" below, all the other sentences/statements that have quotation marks (" ") are copied from the "google translate" version of the help page (link near the top of this post).