How does this minor rule affect my odds?

I play a lot on Bovada and they have one BJ rule that I've never seen factored into rates by the Wizard (Just cause I haven't seen it doesn't mean its not there, but anyways...)

The rule is forced insurance when dealer upcard is A when I'm holding a BJ.

How many decks? Are they shuffled every game?

Which blackjack game did you experience this in - Regular Blackjack, Single-Deck Blackjack, Double-Deck Blackjack, or European Blackjack?

Quote: CrystalMath

How many decks? Are they shuffled every game?

I have not found an answer to that at Bovada, but my assumption is 6+, shuffled either every game or every other. But there could be some fine print somewhere that says otherwise.

Quote: JB

Which blackjack game did you experience this in - Regular Blackjack, Single-Deck Blackjack, Double-Deck Blackjack, or European Blackjack?

Regular Blackjack

Download version or instant-play version?

Quote: JB

Download version or instant-play version?

Instant Play

I was just trying out the instant-play version. Normally when the dealer has an Ace, the Insurance question has a Yes and a No button on the right side of the table.

After several hands, I was dealt this:



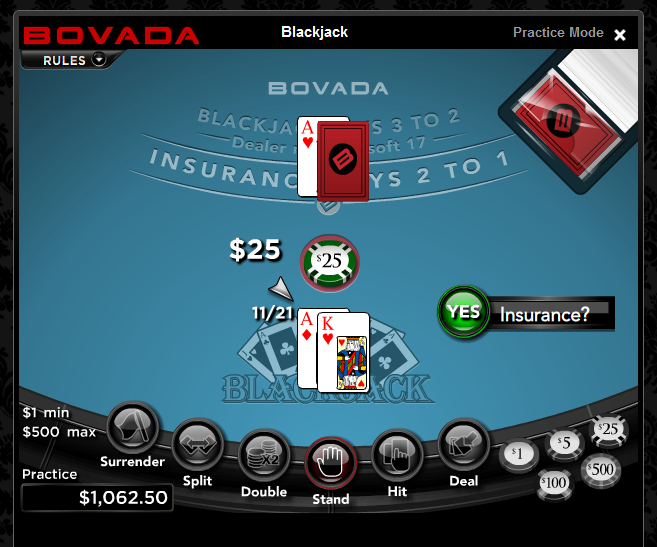
The No button is not there. However, you can decline insurance by clicking the Stand button near the bottom.

Quote: JB

I was just trying out the instant-play version. Normally when the dealer has an Ace, the Insurance question has a Yes and a No button on the right side of the table.

After several hands, I was dealt this:



The No button is not there. However, you can decline insurance by clicking the Stand button near the bottom.

Haha well isn't that tricky. I almost thought my interface was buggy with the missing "no" or something.

Well then just out of curiosity, since I've been playing with this "rule" for the past 1000 games or so, how has it impacted my odds, if anyone can calculate that math

Assuming an 8-deck game (and that I did the math correctly):

The probability of being dealt blackjack against a dealer Ace is 253952/71472960 = 0.003553

The probability of the dealer having blackjack in this situation is 127/413 = 0.307506
The probability of the dealer not having blackjack in this situation is 286/413 = 0.692494

Without insurance, the net win when the dealer has blackjack is 0
Without insurance, the net win when the dealer does not have blackjack is 1.5

With insurance, the net win when the dealer has blackjack is 1
With insurance, the net win when the dealer does not have blackjack is 1

Without insurance, the ER is (0.307506*0) + (0.692494*1.5) = 1.038741
With insurance, the ER is (0.307506*1) + (0.692494*1) = 1

The loss in ER for each such situation is 1.038741 - 1 = 0.038741

The loss in value for the average hand from taking insurance in this situation is 0.003553 * 0.038741 = 0.000138

For 1000 hands that would be an expected additional loss of 0.137651 times your initial bet.

If you were betting $25 a hand, then you lost an additional $3.44 over the last 1000 hands.

Quote: JB

Normally when the dealer has an Ace, the Insurance question has a Yes and a No button on the right side of the table.

...

The No button is not there. However, you can decline insurance by clicking the Stand button near the bottom.

Although you've found a "work-around" I'd suggest letting Bovada know about this. There should be consistancy.

It will be brought to their attention.

Unbelievably interesting, I love math and statistics. I really appreciate your quick response, very educational.

I'll write to the appropriate person there. Meanwhile, "just say stand" to insurance in that situation.

Thats interesting, I come to a different number.

On an 8 deck game, there are 127 tens left in the total of 413 unseen cards.
Hence the probability of a dealers ten in the hole is 127/413. While the insurance bet pays 2:1, your expected return is 127/413 * 3 = 92.25% of the insurance wager.

The scenario of being dealt BJ against A happens with probability (32 / 416) * 2 * (31 / 415) * (128/414) = 0.3553%.
Since you bet half your initial bet on the insurance, a forced insurance on BJ vs A will cost you 0.3553% * 1/2 * 92.25% = 0.1639% of your initial wager per hand.

So which one is correct, 0.1639% or 0.0138% ?