Odds of winning these bets

If I have four bets and I will win the first bet 42% of the time, the second bet 42% of the time, the third bet 48% of the time and the fourth bet 15% of the time. Then what are the odds that I lose all four bets? How about winning just one of them (doesn't matter which one)? Two? How about winning all four of them? Thank you.

Rather than just give you an answer, think of it this way... there are 16 total possibilities...
WWWW
WWWL
WWLW
WWLL
WLWW
WLWL
WLLW
WLLL
LWWW
LWWL
LWLW
LWLL
LLWW
LLWL
LLLW
LLLL
The first one (WWWW) will happen .42 x .42 x .48 x .15= .0127008, or about 1.3% of the time.
Why don't you try and figure out your other answers now....

Hi Roony. Welcome to the forum.

You will lose all four bets 14.86888% of the time.

You will win exactly one bet approximately 37.89% of the time.

You will win exactly two bets approximately 33.89% of the time.

You will win all four bets 1.27008% of the time.


Good luck with your "system."

Quote: EdCollins

You will lose all four bets 14.86888% of the time.
You will win exactly one bet approximately 37.89% of the time.
You will win exactly two bets approximately 33.89% of the time.
You will win all four bets 1.27008% of the time.

Can you "show your work"? Or as I used to have to do in math class... draw a picture of me craning my neck to see the paper of the person sitting in front of me.
Or, better yet, give it to us textually rather in these formulas that don't make much sense to me anyway.

Quote: FleaStiff

Can you "show your work"? Or as I used to have to do in math class... draw a picture of me craning my neck to see the paper of the person sitting in front of me.
Or, better yet, give it to us textually rather in these formulas that don't make much sense to me anyway.

Well, for what it's worth, here is my work:

winning all four bets: 42/100 * 42/100 * 48/100 * 15/100
losing all four bets: 58/100 * 58/100 * 52/100 * 85/100

Notice for my other two answers I said "approximately." My work for this is a computer simulation, for 1 billion trials.

RANDOMIZE TIMER
max_sims = 1000000000

FOR x = 1 TO max_sims
win = 0
rand_number = RND(1, 100)
IF rand_number <= 42 THEN INCR win

rand_number = RND(1, 100)
IF rand_number <= 42 THEN INCR win

rand_number = RND(1, 100)
IF rand_number <= 48 THEN INCR win

rand_number = RND(1, 100)
IF rand_number <= 15 THEN INCR win

IF win = 4 THEN INCR won_all_four
IF win = 0 THEN INCR lost_all_four
IF win = 2 THEN INCR won_two_of_them
IF win = 1 THEN INCR won_one_of_them
NEXT

PRINT "Won all four:"; won_all_four
PRINT "Probability:";won_all_four/max_sims

PRINT "Lost all four:"; lost_all_four
PRINT "Probability:";lost_all_four/max_sims

PRINT "Won just one of them:"; won_one_of_them
PRINT "Probability:";won_one_of_them/max_sims

PRINT "Won just two of them:"; won_two_of_them
PRINT "Probability:";won_two_of_them/max_sims



Program Output:

Won all four: 12,700,208
Probability: .012700208

Lost all four: 148,687,737
Probability: .148687737

Won just one of them: 378,828,971
Probability: .378828971

Won just two of them: 338,971,187
Probability: .338971187

Quote: FleaStiff

Can you "show your work"? Or as I used to have to do in math class... draw a picture of me craning my neck to see the paper of the person sitting in front of me.
Or, better yet, give it to us textually rather in these formulas that don't make much sense to me anyway.

I don't see any reason it would require a simulation. On the other hand, I'm too lazy to do all the calculations manually, so I started with the guidance from SOOPOO and used a spreadsheet. Below is a copy of the spreadsheet, and I suspect you can figure out the formulas for each cell.

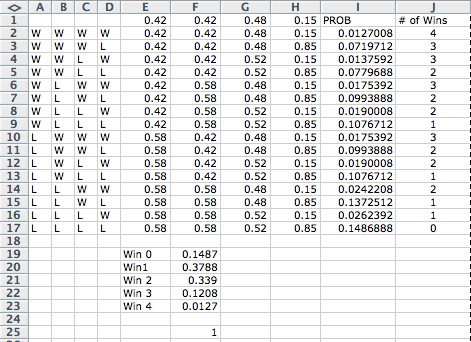
Quote: Doc

I don't see any reason it would require a simulation...

Well, it doesn't REQUIRE a simulation. A simulation is just one of the many ways to arrive at the answer.

Quote: EdCollins

Well, it doesn't REQUIRE a simulation. A simulation is just one of the many ways to arrive at the answer.

Understood. I just wouldn't use a simulation when an explicit calculation of the answer is so straight forward. Do you ordinarily simulate a million rolls of a pair of dice to determine the probability of a roll that totals 7? It's easier, and much clearer, just to calculate the EV as 1/6, I think. The OP's 4-bet question is not quite that simple, but it isn't hard to calculate, and you can see every calculation that is needed represented in the small image of a spreadsheet above. On the other hand, there are many probability questions where explicit calculation becomes impractical or maybe impossible, and that is were most people would use simulations. No?

I usually draw the line at anything I can't actually do in Excel. For computations O(<10^5), I'll do it in Excel. For O(10^6 .. 10^10) or so, I'll write an iterator. For O(>10^11), that's usually too big for an iterator to run through in a reasonable amount of time (on my machine) so I'll simulate. This problem, being O(2^4), is definitely Excel fodder.

Quote: EdCollins

Hi Roony. Welcome to the forum.

You will lose all four bets 14.86888% of the time.

You will win exactly one bet approximately 37.89% of the time.

You will win exactly two bets approximately 33.89% of the time.

You will win all four bets 1.27008% of the time.


Good luck with your "system."

Thank you for your assistance. It's not actually a system however.