Pair during omaha poker

What is the probability of a pair in a 5 card display of shared cards (think of an Omaha game?

Now how about 2 groups of 5 shared cards having at least
One pair?

Quote: doctorpg

What is the probability of a pair in a 5 card display of shared cards (think of an Omaha game?

Now how about 2 groups of 5 shared cards having at least
One pair?
link to original post

doctorpg,

I can answer your first question. Either we have a pair or we don't, so

P(pair) + P(no) = 1

I mention this because P(no) is easier to find and, once we do find it, then

P(pair) = 1 - P(no)

Now we calculate:

P(no) = (52/52)*(48/51)*(44/50)*(40/49)*(36/48)
= 0.5070828332

This is because the 1st card can be any of the 52 cards in the deck. Let's say it is a 3.

The 2nd card then has 3 remaining 3's out of the remaining 51 cards, so that means the 2nd card can be any of 51 - 3 = 48 cards WITHOUT matching the 1st card, so the probability that the first two cards do NOT form a pair is 48/51. Let's say it's a Q.

Now the 3rd can be anything other than one of the 3 3's or 3 Q's out of the remaining 50 cards, so the probability that it does NOT match either of the first two cards is 44/50.

By similar reasoning, the probability that the 4th card does NOT match any of the first three is 40/49, and the probability that the 5th card does NOT match any of the first four is 36/48. Since all of these conditions must be true simultaneously for us NOT to have a pair, we multiply them together, as shown above.

Now

P(pair) = 1 - P(no) = 0.4929171668

This means that about 49.3% of the time, the 5 cards will have at least one pair. Note that this percentage includes higher poker hands that involve at least one pair, so four-of-a-kind, full house, and three-of-a-kind are included, but not a straight, flush, straight flush, or royal flush.

Hope this helps!

Dog Hand

Swell thanks


Now for the second group of 5 cards with no pair in those 5 cards using the same approach ….? Hmmm.

Let me follow Doghand to calculate the second part. The probability of no pair in two 5-card groups is

P(no) x P(no) = 0.507 x0.507 = 0.2570.

Therefore, the probability of at least one pair is

1- 0.257 = 74.3%.

Is this good?

aceside,

If the two 5-card groups were drawn from separate decks, then your answer would be correct. However, I believe doctorpg was asking about the case where both 5-card groups are drawn from the same deck.

If I am mistaken, perhaps doctorpg can let us know.

Dog Hand

Yes ace side is right : same deck

This is funny. In that case of two 5-card groups simultaneously drawing out of a deck, the above calculation of mine may not be accurate enough. There is a correlation between these two groups, so I don’t know how to handle this.

There are C(52,5)=2598960 ways of drawing the first group, and for each way, there are C(47,5)=1533939 ways of drawing the second group. Therefore, there are altogether 2598960x1533939 combinations of these two groups. However, these two groups are identical, so only half of this gigantic number is needed to be considered. Can somebody help with this calculation?

ThatDonGuy must know this.

If there are two five-card boards dealt from the same deck, and the first five card board is defined as having no pairs, then the second five card board is being dealt from the following 47-card deck:

there are 5 ranks in which there are 3 cards (of different suits)
there are 8 ranks in which there are still all 4 cards

Obviously the ranks that have only 3 cards remaining in them are less likely to produce a pair. than the ranks.with four cards remaining

You must calculate the probability of six distinct boards:

1. 5 different ranks with zero from the ranks with 3 cards
2. 5 different ranks with one from the ranks with 3 cards
3. 5 different ranks with two from the ranks with 3 cards
4. 5 different ranks with three from the ranks with 3 cards
5. 5 different ranks with four from the ranks with 3 cards
6. 5 different ranks with all five from the ranks with 3 cards

Simply calculate the probabilities of these six cases and sum them!

Quote: gordonm888

If there are two five-card boards dealt from the same deck, and the first five card board is defined as having no pairs, then the second five card board is being dealt from the following 47-card deck:

there are 5 ranks in which there are 3 cards (of different suits)
there are 8 ranks in which there are still all 4 cards

Obviously the ranks that have only 3 cards remaining in them are less likely to produce a pair. than the ranks.with four cards remaining

You must calculate the probability of six distinct boards:

1. 5 different ranks with zero from the ranks with 3 cards
2. 5 different ranks with one from the ranks with 3 cards
3. 5 different ranks with two from the ranks with 3 cards
4. 5 different ranks with three from the ranks with 3 cards
5. 5 different ranks with four from the ranks with 3 cards
6. 5 different ranks with all five from the ranks with 3 cards

Simply calculate the probabilities of these six cases and sum them!
link to original post

gordonm888,

My attempt to calculate the No Pair probability is as follows:

P(no) = (52/52)*(48/51)*(44/50)*(40/49)*(36/48)*(x6/47)*(x7/46)*(x8/45)*(x9/44)*(x10/43)

with x6 through x10 defined below.

Let's call the ten cards C1, C2, ..., C10, with Hand 1 (H1) containing C1 through C5 and Hand 2 (H2) containing C6 through C10.

The x-variable in each term represents the average number of cards remaining in the deck that do NOT match the previous cards in H2, so x6 = 47, because C6 is the first card in H2, so C6 can be any of the 47 cards remaining in the deck without getting a H2 match..

C7 is now drawn from 46 cards, so

x7 = 46 - n6

where n6 is the number of cards that match C6 still in the deck. Thus, n6 must be either 3 (if C6 does not match any card in H1) or 2 (if C6 matches exactly one card in H1): naturally n6 cannot be 1, because then C6 would have to match 2 cards in H1, so H1 already has a pair.

The probability that c6 DOES match a card in H1 is 15/47, because each of the five cards in H1 is unique, so the deck has 3 more of each of those 5, so 15, and c6 is drawn from a 47-card deck. Therefore, the probability that c6 does NOT match any card in H1 is 1 - 15/47 = 32/47.

This means that, on average, the deck has

n6 = 3*32/47 + 2*15/47 = 3*(1 - 15/47) + 2*15/47 = 3 - 15/47

cards remaining in the deck that match C6. Plugging this into the x7 equation gives

x7 = 46 - n6 = 46 - (3 - 15/47) = 43 + 15/47.

Continuing, we can say

x8 = 45 - n6 - n7

where n7 is the number of remaining cars that match C7.

Using similar reasoning as above, we get

n7 = 3 - 15/46

Here, the denominator on the fraction is 46, because C7 is drawn from a deck of 46 cards, so the probability that c7 DOES match a card in H1 is 15/46 (still 15 matching cards for the H1 cards).

Then we get

x8 = 45 - n6 - n7 = 45 - (3 - 15/47) - (3 - 15/46) = 39 + 15/47 + 15/46

By analogy, we get the following equations for x9 & x10:

x9 = 44 - n6 - n7 - n8 = 44 - (3 - 15/47) - (3 - 15/46) - (3 - 15/45) = 35 + 15/47 + 15/46 + 15/45

x10 = 43 - n6 - n7 - n8 - n9 = 43 - (3 - 15/47) - (3 - 15/46) - (3 - 15/45) - (3 - 15/44) = 31 + 15/47 + 15/46 + 15/45 + 15/44

Plugging into Excel gives:


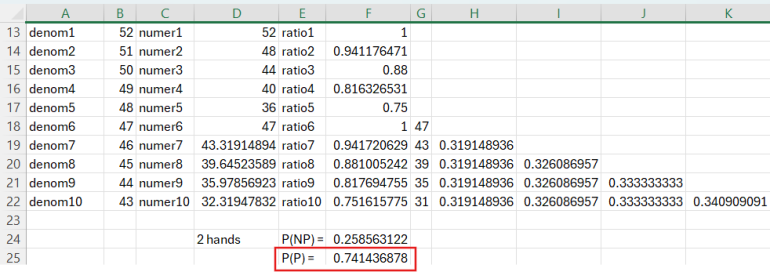
This indicates that the "No Pair" probability is about 74.1%. I will mention that this is close to the 74.3% value that aceside mentioned in his post.

Having said all that, I am not satisfied that my method is correct. I wrote VBA code to simulate the problem, and it consistently shows values just slightly smaller in the 4th decimal place:

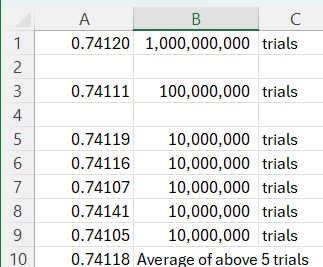
The billion-round sim, which took about 12 minutes to run, gives 0.74120 for the Pair Probability.

Here is the code I wrote: sorry that the colors and indentation are not preserved:
Public Sub PairProb2()
' Given two 5-card hands from a single deck,
' what is the probability of a pair in at least one of the hands?
Dim R(0 To 51) As Integer ' Rank of card: 0 to 12
Dim i As Integer, j As Integer, k As Integer, temp As Integer
Dim N As Long, Ntot As Long, NoPair As Long
Dim PPair As Double, PNoPair As Double

' Create initial deck
For i = 0 To 12
For j = 0 To 3
k = 13 * j + i
R(k) = i
Next j
Next i

' Initialize
Ntot = 1000000000: NoPair = 0

For N = 1 To Ntot
' Shuffle using Fisher-Yates algorithm
For i = 0 To 9 ' Only need the first 10 cards
' Pick a random number from i to 51
j = Int((52 - i) * Rnd()) + i
' Swap R(j) and R(i)
temp = R(i)
R(i) = R(j)
R(j) = temp
Next i
' Check for pair among cards 0, 1, 2, 3, 4
For i = 1 To 4
For j = 0 To i - 1
If R(j) = R(i) Then GoTo Pair: ' Pair
Next j
Next i
' Check for pair among cards 5, 6, 7, 8, 9
For i = 6 To 9
For j = 5 To i - 1
If R(j) = R(i) Then GoTo Pair: ' Pair
Next j
Next i
' No Pair
NoPair = NoPair + 1
Pair:
Next N

PNoPair = CDbl(NoPair) / CDbl(Ntot)
PPair = 1 - PNoPair
Cells(1, 1) = PPair ' Output pair prob in A1

End Sub


Hope this helps!

Dog Hand

This is convincing! Indeed, there is a correlation between these two 5-card hands that are drawn from the same deck. It took me a long time to digest this.

The result should apply to the game of Caribbean Stud poker, not Omaha poker though. In Omaha poker, each player is dealt four cards each, but there is a community board of five cards for players to pick out three of them. This situation will enhance the correlation, I believe. This is interesting.

In Omaha poker, let me follow DogHand again to calculate the probability of a player having at least a pair in his 4-card hand and his 5-card community board. It is

65.6%.