Poll
 | 5 votes (50%) | ||
 | 2 votes (20%) | ||
| No votes (0%) | |||
 | 1 vote (10%) | ||
 | 1 vote (10%) | ||
 | 1 vote (10%) | ||
 | 4 votes (40%) | ||
 | 3 votes (30%) | ||
 | 2 votes (20%) | ||
 | 4 votes (40%) |
10 members have voted
- Both teams consist of two players each. I will call them team 1 and team 2 with player A and player B on each team.
- When any player has the serve, he continues to serve until his team misses a point. With each win, the serving team gets a point. With a loss, the serve rotates to the next player. So, only the serving team can earn points.
- Team 1 player B serves. When the other team wins, go to rule 4.
- Team 2 player A serves. When the other team wins, go to rule 5.
- Team 2 player B serves. When the other team wins, go to rule 6.
- Team 1 player A serves. When the other team wins, go to rule 3.
- Repeat rules 3-6 until either team gets to 11 points.
There is also a rule that the winning team must win by 2, but to keep the math simple, let's forget that. I think it's a negligible effect.
Assuming each team always has a 50% chance of winning each serve, what is the probability team 1 wins?
Warning that this is a tedious problem with no simple solution that I can see.
The question for the poll is what is the answer. Multiple votes allowed.
How often does a serving team with 11 straight points?Quote: WizardBefore I get to the question, let me review the pickleball scoring rules.
- Both teams consist of two players each. I will call them team 1 and team 2 with player A and player B on each team.
- When any player has the serve, he continues to serve until his team misses a point. With each win, the serving team gets a point. With a loss, the serve rotates to the next player. So, only the serving team can earn points.
- Team 1 player B serves. When the other team wins, go to rule 4.
- Team 2 player A serves. When the other team wins, go to rule 5.
- Team 2 player B serves. When the other team wins, go to rule 6.
- Team 1 player A serves. When the other team wins, go to rule 3.
- Repeat rules 3-6 until either team gets to 11 points.
There is also a rule that the winning team must win by 2, but to keep the math simple, let's forget that. I think it's a negligible effect.
Assuming each team always has a 50% chance of winning each serve, what is the probability team 1 wins?
Warning that this is a tedious problem with no simple solution that I can see.
The question for the poll is what is the answer. Multiple votes allowed.
link to original post
Quote: AxelWolfHow often does a serving team with 11 straight points?
link to original post
Assuming a 50% chance of winning each serve, 1 in 2^11 = 1 in 2048.
Quote: SOOPOOI canít do the math. But I know the advantage will not even be 1%.
link to original post
Not sure itíll actually be an advantage.
Quote: unJonQuote: SOOPOOI canít do the math. But I know the advantage will not even be 1%.
link to original post
Not sure itíll actually be an advantage.
link to original post
Perhaps. But it wonít be a disadvantage by 1% either.
Quote: WizardBefore I get to the question, let me review the pickleball scoring rules.
- Both teams consist of two players each. I will call them team 1 and team 2 with player A and player B on each team.
- When any player has the serve, he continues to serve until his team misses a point. With each win, the serving team gets a point. With a loss, the serve rotates to the next player. So, only the serving team can earn points.
- Team 1 player B serves. When the other team wins, go to rule 4.
- Team 2 player A serves. When the other team wins, go to rule 5.
- Team 2 player B serves. When the other team wins, go to rule 6.
- Team 1 player A serves. When the other team wins, go to rule 3.
- Repeat rules 3-6 until either team gets to 11 points.
link to original post
Actually, that's not quite right. You need to move item 3 down to item 6, and change the "go to rule" numbers accordingly. This used to be how badminton doubles was played back before it switched to "every rally scored a point" rules. The side that serves first loses the serve when the other team wins - then it's two losses per side.
Edit: I could have sworn the original post said that both team A players serve, then both team B players serve. Wizard has it right.
I welcome challenges to my figure above.
Quote: WizardWith no affirmative replies so far, I'll just say that I believe team B has the advantage.
0.476816269
I welcome challenges to my figure above.
link to original post
The above is based on the "11-10 is a valid ending score"
Note that the following calculations do include the "must win by 2" rule.
If the game reaches 10-10, the probability that Team A will win depends on who was serving when the 20th point was scored:
A1: 30 / 43
A2: 45 / 86
B1: 13 / 43
B2: 41 / 86
I thought I was seriously imagining things, but I calculated this in two different ways, and got the same answer...and now I see that Wizard agrees with me; Team B has the advantage. Not much, but it does have one.
The strange thing is, the advantage changes depending on how many points you need to win. For example, if the game is to 10 instead of 11, Team A has the advantage.
| Points to win | Probability that the first servers win |
|---|---|
| 3 | 1/2 + 1 / 597 |
| 4 | 1/2 - 1 / 4,335 |
| 5 | 1/2 - 1 / 10,665 |
| 6 | 1/2 - 1 / 79,305 |
| 7 | 1/2 + 1 / 2,978,169 |
| 8 | 1/2 + 1 / 1,996,054 |
| 9 | 1/2 + 1 / 9,977,842 |
| 10 | 1/2 + 1 / 204,318,478 |
| 11 | 1/2 - 1 / 403,569,770 |
| 12 | 1/2 - 1 / 1,346,295,818 |
| 13 | 1/2 - 1 / 12,533,738,097 |
| 14 | 1/2 + 1 / 111,361,069,974 |
| 15 | 1/2 + 1 / 198,820,463,562 |
| 16 | 1/2 + 1 / 1,204,567,620,094 |
| 17 | 1/2 + 1 / 225,158,568,342,135 |
| 18 | 1/2 - 1 / 33,146,363,370,199 |
| 19 | 1/2 - 1 / 138,925,552,850,011 |
| 20 | 1/2 - 1 / 1,857,348,465,754,418 |
| 21 | 1/2 + 1 / 6,786,416,313,075,118 |
| 22 | 1/2 + 1 / 18,188,321,986,452,131 |
| 23 | 1/2 + 1 / 137,669,250,986,749,514 |
| 24 | 1/2 - 1 / 2,514,667,007,931,396,949 |
| 25 | 1/2 - 1 / 2,690,966,128,118,204,853 |
Quote: ThatDonGuy
Note that the following calculations do include the "must win by 2" rule.
link to original post
I can't compare answers because I don't follow that rule. Would it be difficult for you to run the calculations without that rule?
Quote: WizardQuote: ThatDonGuy
Note that the following calculations do include the "must win by 2" rule.
link to original post
I can't compare answers because I don't follow that rule. Would it be difficult for you to run the calculations without that rule?
link to original post
| Points to win | Probability that the first servers win |
|---|---|
| 3 | 1/2 + 1 / 6,250 |
| 4 | 1/2 - 1 / 3,472 |
| 5 | 1/2 - 1 / 15,319 |
| 6 | 1/2 - 1 / 204,730 |
| 7 | 1/2 + 1 / 907,923 |
| 8 | 1/2 + 1 / 2,421,742 |
| 9 | 1/2 + 1 / 18,396,274 |
| 10 | 1/2 - 1 / 423,643,430 |
| 11 | 1/2 - 1 / 400,784,493 |
| 12 | 1/2 - 1 / 2,058,584,254 |
| 13 | 1/2 - 1 / 49,407,037,232 |
| 14 | 1/2 + 1 / 75,384,230,134 |
| 15 | 1/2 + 1 / 261,659,608,358 |
| 16 | 1/2 + 1 / 2,554,882,096,168 |
| 17 | 1/2 - 1 / 19,115,442,346,052 |
| 18 | 1/2 - 1 / 37,145,223,618,262 |
| 19 | 1/2 - 1 / 232,268,896,097,961 |
| 20 | 1/2 + 1 / 71,000,106,769,456,703 |
| 21 | 1/2 + 1 / 5,991,638,632,532,946 |
| 22 | 1/2 + 1 / 25,929,872,189,853,977 |
| 23 | 1/2 + 1 / 374,131,141,261,224,386 |
| 24 | 1/2 - 1 / 1,179,230,184,390,310,444 |
| 25 | 1/2 - 1 / 3,314,087,672,236,851,971 |
Note that my answer under "Challenge Accepted!" did not use the "win by 2" rule.
How did you calculate yours?
Quote: ThatDonGuy
How did you calculate yours?
link to original post
Thank you. We still disagree. I have a feeling you're right. I will review my work tomorrow.
To answer your question, I basically used a Markov chain.
Still assuming that this is WIN BY ONE, not by TWO, and playing to 11. So for example, IF the players are of the same skill level, and.....
a) Each Server Wins ONE and only ONE Serve each time, then:
Team 1 wins, 11 - 10.
b) Each Server Wins TWO and only TWO Serves each time, then:
Team 2 wins, 10 - 11.
c) Each Server Wins THREE and only THREE Serves each time, then:
Team 2 wins, 9 - 11
d) Each Server Wins FOUR and only FOUR Serves each time, then:
Team 1 wins, 11 - 8.
Quote: ThatDonGuy
Here is the table where you can win by 1 point:
Points
to winProbability that
the first servers win3 1/2 + 1 / 6,250 4 1/2 - 1 / 3,472 5 1/2 - 1 / 15,319 6 1/2 - 1 / 204,730 7 1/2 + 1 / 907,923 8 1/2 + 1 / 2,421,742 9 1/2 + 1 / 18,396,274 10 1/2 - 1 / 423,643,430 11 1/2 - 1 / 400,784,493 12 1/2 - 1 / 2,058,584,254 13 1/2 - 1 / 49,407,037,232 14 1/2 + 1 / 75,384,230,134 15 1/2 + 1 / 261,659,608,358 16 1/2 + 1 / 2,554,882,096,168 17 1/2 - 1 / 19,115,442,346,052 18 1/2 - 1 / 37,145,223,618,262 19 1/2 - 1 / 232,268,896,097,961 20 1/2 + 1 / 71,000,106,769,456,703 21 1/2 + 1 / 5,991,638,632,532,946 22 1/2 + 1 / 25,929,872,189,853,977 23 1/2 + 1 / 374,131,141,261,224,386 24 1/2 - 1 / 1,179,230,184,390,310,444 25 1/2 - 1 / 3,314,087,672,236,851,971
link to original post
Thank you! I agree! Now onto the case where the player must win by 2.
I definitely owe you a beer for this one.
Well sure, but what about my detailed arithmetic analysis ? Is that worth a half can of PBR ?Quote: Wizard
I definitely owe you a beer for this one.
;-)
1. What is the probability the serving team wins if player 1 on the team has the serve?
2. What is the probability the serving team wins if player 2 on the team has the serve?
Quote: WizardTo ask a sub-question, let's say it's deuce (or 10-10). Winning team must win by 2.
1. What is the probability the serving team wins if player 1 on the team has the serve?
2. What is the probability the serving team wins if player 2 on the team has the serve?
link to original post
Er, this one's been answered...
Quote: ThatDonGuy
Sorry, I forgot about that. I agree with your figures.
First server with advantage = 0.872093023 probability of winning.
Second server with advantage = 0.744186047 probability of winning.
First server with disadvantage = 0.511627907 probability of winning.
Second server with disadvantage = 0.325581395 probability of winning.
Probability team to serve first wins = 0.5 - (1/229,863) = 0.4999956.
Quote: WizardFor what it's worth, here is my probability of the original question but with the "win by two rule."
Probability team to serve first wins = 0.5 - (1/229,863) = 0.4999956.
link to original post
I checked it with two different methods, and both times, I get 1/2 - 1/403,569,770
Quote: ThatDonGuy
I checked it with two different methods, and both times, I get 1/2 - 1/403,569,770
link to original post
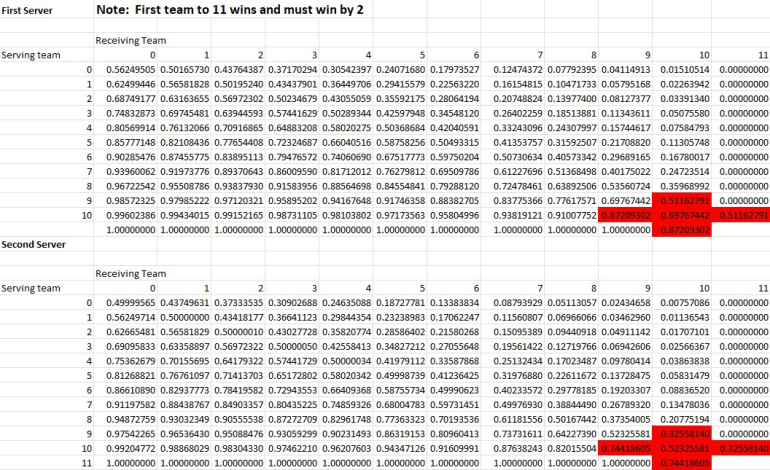
Here is a screenshot of every possible state of the game. The answer to the original question in the 0/0 second server cell (0.499999565). The situations where the player is directly affected by the "win by 2" rule are shown in red cells.
I would be keen to know the situation closest to those red situations you disagree with.
Thank you.
Quote: WizardWould you agree with the following end game situations...
First server with advantage = 0.872093023 probability of winning.
Second server with advantage = 0.744186047 probability of winning.
First server with disadvantage = 0.511627907 probability of winning.
Second server with disadvantage = 0.325581395 probability of winning.
link to original post
I get those numbers as well.
Quote: WizardQuote: ThatDonGuy
I checked it with two different methods, and both times, I get 1/2 - 1/403,569,770
link to original post
Here is a screenshot of every possible state of the game. The answer to the original question in the 0/0 second server cell (0.499999565). The situations where the player is directly affected by the "win by 2" rule are shown in red cells.
I would be keen to know the situation closest to those red situations you disagree with.
Thank you.
link to original post
All of the red numbers are correct.
However, both of your 10-0 numbers are different than mine (the 10-1 numbers are correct, as are all of the numbers in the receiving team score 1-9 columns as well).
This would cause all of the other receiving team score 0 numbers to be off as well, assuming you are using the "work backwards" method.
Quote: ThatDonGuyAll of the red numbers are correct.
However, both of your 10-0 numbers are different than mine (the 10-1 numbers are correct, as are all of the numbers in the receiving team score 1-9 columns as well).
This would cause all of the other receiving team score 0 numbers to be off as well, assuming you are using the "work backwards" method.
link to original post
Thank you! That helped me find my mistake. I was not correctly handling the situation where the score was 10-0 and the team with 10 lost and the other team went onto score 11 points before losing the serve.
This is a Markov chain solution, where the probabilities of things depend on the probabilities of other things.
I found two ways to do this (and used both to confirm the numbers I got). Here is the easiest way, which is also how you can do it in Excel:
Let A1 and A2 be the players on Team A, which is the team that serves first, and B1 and B2 the players on Team B.
A2 will serve first; the service order will then be A2, B1, B2, A1, A2, B1, B2, and so on
Let P(A, B, S) be the probability that Team A wins with a score of A-B and person S serving.
For example, P(0, 0, A2) is the probability that Team A wins with a score of 0-0 and A2 serving; not coincidentally, this is the condition at the start of the game, so P(0, 0, A2) is the solution to our problem.
First, we need to figure out P(10, 10, S) for all four values of S (i.e. A1, A2, B1, and B2).
This is done with simultaneous equations.
There are 12 possible "states" before the game ends:
(1) through (4) are A1, A2, B1, and B2 serving with the score tied;
(5) through (8) are A1, A2, B1, and B2 serving with Team A ahead;
(9) through (12) are A1, A2, B1, and B2 serving with Team B ahead
Notice that, in the following 12 equations, the first value in the sum is the case where the server wins the point, and the second value is the case where the server loses
P(1) = 1/2 P(5) + 1/2 P(2)
P(2) = 1/2 P(6) + 1/2 P(3)
P(3) = 1/2 P(11) + 1/2 P(4)
P(4) = 1/2 P(12) + 1/2 P(1)
Note that, in states 5 and 6, if the server wins, Team A wins the game
P(5) = 1/2 x 1 + 1/2 P(6)
P(6) = 1/2 x 1 + 1/2 P(7)
P(7) = 1/2 P(3) + 1/2 P(8)
P(8) = 1/2 P(4) + 1/2 P(5)
P(9) = 1/2 P(1) + 1/2 P(10)
P(10) = 1/2 P(2) + 1/2 P(11)
Note that, in states 11 and 12, if the server wins, Team B wins the game
P(11) = 1/2 x 0 + 1/2 x P(12)
P(12) = 1/2 x 0 + 1/2 x P(9)
Solving these gets:
P(1) = 30 / 43
P(2) = 45 / 86
P(3) = 13 / 43
P(4) = 41 / 86
There are values for P(5) through P(12), but they are unnecessary for this problem
Now, to solve the problem, start with assigning the P(10, 10, S) values from what we just solved:
P(10, 10, A1) = 30 / 43
P(10, 10, A2) = 45 / 86
P(10, 10, B1) = 13 / 43
P(10, 10, B2) = 41 / 86
Also note that P(11, B, S) = 1 for all B < 10 and all servers S, and P(A, 11, S) = 0 for all A < 10 and all servers S
To figure out the remaining values, assume A1 is serving with the score A-B
1/2 of the time, A1 will win a point (and keep the serve), so the state will be (A+1, B, A1)
1/4 of the time, A1 will lose, but A2 will win a point, so the state will be (A+1, B, A2)
1/8 of the time, A1 and A2 will both lose, but B1 will win a point, so the state will be (A, B+1, B1)
1/16 of the time, A1, A2, and B1 will all lose, but B2 will win a point, so the state will be (A, B+1, B2)
1/16 of the time, all four will lose, so the state will return to (A, B, A1)
P(A, B, A1) = 1/2 P(A+1, B, A1) + 1/4 P(A+1, B, A2) + 1/8 P(A, B+1, B1) + 1/16 P(A, B+1, B2) + 1/16 P(A, B, A1)
(1 - 1/16) P(A, B, A1) = 1/2 P(A+1, B, A1) + 1/4 P(A+1, B, A2) + 1/8 P(A, B+1, B1) + 1/16 P(A, B+1, B2)
P(A, B, A1) = 16/15 (1/2 P(A+1, B, A1) + 1/4 P(A+1, B, A2) + 1/8 P(A, B+1, B1) + 1/16 P(A, B+1, B2))
= 8/15 P(A+1, B, A1) + 4/15 P(A+1, B, A2) + 2/15 P(A, B+1, B1) + 1/15 P(A, B+1, B2)
As you can see, each value can be determined by the sum of values where the sum of the two scores is 1 higher
The only possible score of 20 we are concerned with is 10-10, and we already know the P(10, 10, S) values
Calculate the values where the sum of the scores is 19 (i.e. (10, 9, S) and (9, 10, S)), then 18, and 17, and so on down to zero.
The solution, as stated above, is P(0, 0, A2).
The second method, which does not require knowing the P(10, 10, S) numbers in advance, is using more simultaneous equations.
For example, at the start, either A2 wins a point, and the state is P(1, 0, A2), or loses, and the state is P(0, 0, B1);
P(0, 0, A2) = P(1, 0, A2) + P(0, 0, B1)
Do this for all of the possible states, keeping in mind that P(11, 10, S) is the same as P(10, 9, S) as if A scores, A wins, and if B scores, the score is tied and either team needs to get a 2-point lead to win.
This is 484 equations in 484 unknowns.
Short Answer (Approximation): About 52% (slightly over 50%).
Detailed Reasoning:
This is a complex probability problem because it involves a cyclical serving pattern and a "race" to 11 points with only the serving team able to score. Each rally is a 50-50 proposition, and the serve rotates through four players in a fixed order whenever the serving team loses a rally.
(...)
See the link above for the very detailed answer from ChatGPT. This is using the o1 model and took 1 minute and 4 seconds to generate.
Bonus information: If you click the link to see the answer, there's a subtle link before the answer "Thought about pickleball scoring probability for 1m 4s". Click here to see how it even reasoned before coming to the detailed response.


