How do I calculate variance for a combination of games? Is it additive or can I do the average?
What is mean is, say I play 30 rounds of a game that has 1.4 variance and 200 rounds of a game that has 2.3 variance.
For risk calculation purposes, can I do the average, so ((1.4*30) + (2.3*200)) / 230 = 2.18 ?
Thanks
The individual variances of all wagers can be added to get the variance of the sum of the all wagers. So your addition is correct. But, dividing the total variance by 230 is not meaningful. As an extreme example, say you make 1 bet with variance of 1.0 and 99 bets with variance zero. It isn't useful to know that the average variance for this series of bets is 1/100. Adding zero-variance wagers does not reduce your risk. Variance per wager is not germane to risk management. Your total variance for the series of wagers is the important factor. The average is not.Quote: gunbjHey guys,
How do I calculate variance for a combination of games? Is it additive or can I do the average?
What is mean is, say I play 30 rounds of a game that has 1.4 variance and 200 rounds of a game that has 2.3 variance.
For risk calculation purposes, can I do the average, so ((1.4*30) + (2.3*200)) / 230 = 2.18 ?
Thanks
link to original post
Quote: MentalThe individual variances of all wagers can be added to get the variance of the sum of the all wagers. So your addition is correct. But, dividing the total variance by 230 is not meaningful. As an extreme example, say you make 1 bet with variance of 1.0 and 99 bets with variance zero. It isn't useful to know that the average variance for this series of bets is 1/100. Adding zero-variance wagers does not reduce your risk. Variance per wager is not germane to risk management. Your total variance for the series of wagers is the important factor. The average is not.Quote: gunbjHey guys,
How do I calculate variance for a combination of games? Is it additive or can I do the average?
What is mean is, say I play 30 rounds of a game that has 1.4 variance and 200 rounds of a game that has 2.3 variance.
For risk calculation purposes, can I do the average, so ((1.4*30) + (2.3*200)) / 230 = 2.18 ?
Thanks
link to original post
link to original post
Thank you very much, i suspected I was doing something wrong.
Usually for a rough risk calculation I take the variance of the game and input in the formula RoR = e^((-2*Edge*(Bankroll / Avg Bet)) / VAR)
But how would that work with this variance combination addition?
If you need to get a SD value that will help you calculate the ROR, then it seems to me that the variances between each other should be multiplied and not added
ror = ((sd-ev)/(sd+ev))^(bank/sd)
* but this formula is only suitable if you have a positive ev
Quote: DobrijWhat value do you want to get?
If you need to get a SD value that will help you calculate the ROR, then it seems to me that the variances between each other should be multiplied and not added
ror = ((sd-ev)/(sd+ev))^(bank/sd)
* but this formula is only suitable if you have a positive ev
link to original post
Yes, basically Iím trying to calculate the effect that playing a negative EV game as cover for a certain amount of time has on RoR.
To keep the numbers I gave above, letís say I play $100 for 30 rounds of a -1.5% edge game that has 1.4 variance and $120 for 200 rounds of a +2.5% game with 2.3 variance.
I want to be able to calculate the risk of the whole play, considering how the -ev game affects my risk.
The RoR formula that you cite is just an approximation, and that approximation is only good under certain conditions. You cannot easily combine games with quite different EVs and get some kind of simple hybrid RoR formula.Quote: gunbjQuote: DobrijWhat value do you want to get?
If you need to get a SD value that will help you calculate the ROR, then it seems to me that the variances between each other should be multiplied and not added
ror = ((sd-ev)/(sd+ev))^(bank/sd)
* but this formula is only suitable if you have a positive ev
link to original post
Yes, basically Iím trying to calculate the effect that playing a negative EV game as cover for a certain amount of time has on RoR.
To keep the numbers I gave above, letís say I play $100 for 30 rounds of a -1.5% edge game that has 1.4 variance and $120 for 200 rounds of a +2.5% game with 2.3 variance.
I want to be able to calculate the risk of the whole play, considering how the -ev game affects my risk.
link to original post
But you are on the right track combining variance. After a sufficiently large number of wagers, the Std. Dev. of your total play becomes well defined, and is given by the square root of total variance. This is the SD around your expected gain/loss. You can get that by summing the expected gain/loss of your two sessions. If a 3 SD negative deviation from that expected loss does not ruin you, then your overall RoR is low.
However, this shows that you cannot simply combine two different plays in one RoR formula. Let us say your cover play is expected to cost you 1000 units and your +EV play is expected to gain you 5000 units. You only have 500 units of bankroll. Clearly, your RoR depend entirely on which order you do the two plays.
Quote: MentalThe RoR formula that you cite is just an approximation, and that approximation is only good under certain conditions. You cannot easily combine games with quite different EVs and get some kind of simple hybrid RoR formula.Quote: gunbjQuote: DobrijWhat value do you want to get?
If you need to get a SD value that will help you calculate the ROR, then it seems to me that the variances between each other should be multiplied and not added
ror = ((sd-ev)/(sd+ev))^(bank/sd)
* but this formula is only suitable if you have a positive ev
link to original post
Yes, basically Iím trying to calculate the effect that playing a negative EV game as cover for a certain amount of time has on RoR.
To keep the numbers I gave above, letís say I play $100 for 30 rounds of a -1.5% edge game that has 1.4 variance and $120 for 200 rounds of a +2.5% game with 2.3 variance.
I want to be able to calculate the risk of the whole play, considering how the -ev game affects my risk.
link to original post
But you are on the right track combining variance. After a sufficiently large number of wagers, the Std. Dev. of your total play becomes well defined, and is given by the square root of total variance. This is the SD around your expected gain/loss. You can get that by summing the expected gain/loss of your two sessions. If a 3 SD negative deviation from that expected loss does not ruin you, then your overall RoR is low.
However, this shows that you cannot simply combine two different plays in one RoR formula. Let us say your cover play is expected to cost you 1000 units and your +EV play is expected to gain you 5000 units. You only have 500 units of bankroll. Clearly, your RoR depend entirely on which order you do the two plays.
link to original post
Thanks, yeah I figured it wasnít that easy.
I understand the concept but could you please give an example from the numbers I gave so I can see better what you mean?
Sorry to bother, but unfortunately Iím a bit slow on these things.
Quote: gunbjQuote: MentalThe RoR formula that you cite is just an approximation, and that approximation is only good under certain conditions. You cannot easily combine games with quite different EVs and get some kind of simple hybrid RoR formula.Quote: gunbjQuote: DobrijWhat value do you want to get?
If you need to get a SD value that will help you calculate the ROR, then it seems to me that the variances between each other should be multiplied and not added
ror = ((sd-ev)/(sd+ev))^(bank/sd)
* but this formula is only suitable if you have a positive ev
link to original post
Yes, basically Iím trying to calculate the effect that playing a negative EV game as cover for a certain amount of time has on RoR.
To keep the numbers I gave above, letís say I play $100 for 30 rounds of a -1.5% edge game that has 1.4 variance and $120 for 200 rounds of a +2.5% game with 2.3 variance.
I want to be able to calculate the risk of the whole play, considering how the -ev game affects my risk.
link to original post
But you are on the right track combining variance. After a sufficiently large number of wagers, the Std. Dev. of your total play becomes well defined, and is given by the square root of total variance. This is the SD around your expected gain/loss. You can get that by summing the expected gain/loss of your two sessions. If a 3 SD negative deviation from that expected loss does not ruin you, then your overall RoR is low.
However, this shows that you cannot simply combine two different plays in one RoR formula. Let us say your cover play is expected to cost you 1000 units and your +EV play is expected to gain you 5000 units. You only have 500 units of bankroll. Clearly, your RoR depend entirely on which order you do the two plays.
link to original post
Thanks, yeah I figured it wasnít that easy.
I understand the concept but could you please give an example from the numbers I gave so I can see better what you mean?
Sorry to bother, but unfortunately Iím a bit slow on these things.
link to original post
$100 for 30 rounds of a -1.5% edge with 1.4 variance
expected loss =100*30*-.015 = -$45
variance = ($100^2)*1.4*30 = 420,000($^2)
$120 for 200 rounds of a +2.5% game with 2.3 variance
expected gain =120*200*.025 = $600
variance = ($120^2)*2.3*200= 6,624,000($^2)
total EV = 600 - 45 = $555
total variance = (6,624,000 + 420,000)($^2)
std dev = sqrt(var) = sqrt(6624000 + 420000) =$2,654
Note that units of variance are dollars squared and units of SD are simple dollars.
Your 3 SD range is (555-(3*2654)) to (555+(3*2654)) so you need a bankroll of $7404 to avoid being busted by any thing less than a 3 SD swing.
Technically, this SD range refers to the final bankroll. There is some chance that you will be down $8000 at some point, but recover to be down only $7000, which puts you within 3 SD of expectation. But, you are still ruined with a $7404 bankroll.
Note that your variance is dominated by the +EV session, not your -EV session. If you used $10 chips as units, then your variance numbers are reduced by a factor of 100 and your SD becomes 265.4 units. The choice of units does not effect the bankroll requirements stated as dollars.
Quote: MentalQuote: gunbjQuote: MentalThe RoR formula that you cite is just an approximation, and that approximation is only good under certain conditions. You cannot easily combine games with quite different EVs and get some kind of simple hybrid RoR formula.Quote: gunbjQuote: DobrijWhat value do you want to get?
If you need to get a SD value that will help you calculate the ROR, then it seems to me that the variances between each other should be multiplied and not added
ror = ((sd-ev)/(sd+ev))^(bank/sd)
* but this formula is only suitable if you have a positive ev
link to original post
Yes, basically Iím trying to calculate the effect that playing a negative EV game as cover for a certain amount of time has on RoR.
To keep the numbers I gave above, letís say I play $100 for 30 rounds of a -1.5% edge game that has 1.4 variance and $120 for 200 rounds of a +2.5% game with 2.3 variance.
I want to be able to calculate the risk of the whole play, considering how the -ev game affects my risk.
link to original post
But you are on the right track combining variance. After a sufficiently large number of wagers, the Std. Dev. of your total play becomes well defined, and is given by the square root of total variance. This is the SD around your expected gain/loss. You can get that by summing the expected gain/loss of your two sessions. If a 3 SD negative deviation from that expected loss does not ruin you, then your overall RoR is low.
However, this shows that you cannot simply combine two different plays in one RoR formula. Let us say your cover play is expected to cost you 1000 units and your +EV play is expected to gain you 5000 units. You only have 500 units of bankroll. Clearly, your RoR depend entirely on which order you do the two plays.
link to original post
Thanks, yeah I figured it wasnít that easy.
I understand the concept but could you please give an example from the numbers I gave so I can see better what you mean?
Sorry to bother, but unfortunately Iím a bit slow on these things.
link to original post
$100 for 30 rounds of a -1.5% edge with 1.4 variance
expected loss =100*30*-.015 = -$45
variance = ($100^2)*1.4*30 = 420,000($^2)
$120 for 200 rounds of a +2.5% game with 2.3 variance
expected gain =120*200*.025 = $600
variance = ($120^2)*2.3*200= 6,624,000($^2)
total EV = 600 - 45 = $555
total variance = (6,624,000 + 420,000)($^2)
std dev = sqrt(var) = sqrt(6624000 + 420000) =$2,654
Note that units of variance are dollars squared and units of SD are simple dollars.
Your 3 SD range is (555-(3*2654)) to (555+(3*2654)) so you need a bankroll of $7404 to avoid being busted by any thing less than a 3 SD swing.
Technically, this SD range refers to the final bankroll. There is some chance that you will be down $8000 at some point, but recover to be down only $7000, which puts you within 3 SD of expectation. But, you are still ruined with a $7404 bankroll.
Note that your variance is dominated by the +EV session, not your -EV session. If you used $10 chips as units, then your variance numbers are reduced by a factor of 100 and your SD becomes 265.4 units. The choice of units does not effect the bankroll requirements stated as dollars.
link to original post
Thatís great, thank you for taking the time, now I understand.
How can I use this for ďplay foreverĒ RoR?
Because I guess as I increase the number of rounds the -3sd from the mean is not going to give a usable number anymore, cause it goes too much in the positive, if I get this right?
Also, and I guess here it goes very hard really fast, is it possible to account for a spread?
What I mean is: what if instead of flat betting $100 in the -EV game I were to spread from say 25 to 500, giving an average of $100. That would also affect risk correct? And it wouldnít be the same as calculating it for a flat bet? Meaning calculating risk from the average bet would not work?
Quote: gunbjQuote: MentalQuote: gunbjQuote: MentalThe RoR formula that you cite is just an approximation, and that approximation is only good under certain conditions. You cannot easily combine games with quite different EVs and get some kind of simple hybrid RoR formula.Quote: gunbjQuote: DobrijWhat value do you want to get?
If you need to get a SD value that will help you calculate the ROR, then it seems to me that the variances between each other should be multiplied and not added
ror = ((sd-ev)/(sd+ev))^(bank/sd)
* but this formula is only suitable if you have a positive ev
link to original post
Yes, basically Iím trying to calculate the effect that playing a negative EV game as cover for a certain amount of time has on RoR.
To keep the numbers I gave above, letís say I play $100 for 30 rounds of a -1.5% edge game that has 1.4 variance and $120 for 200 rounds of a +2.5% game with 2.3 variance.
I want to be able to calculate the risk of the whole play, considering how the -ev game affects my risk.
link to original post
But you are on the right track combining variance. After a sufficiently large number of wagers, the Std. Dev. of your total play becomes well defined, and is given by the square root of total variance. This is the SD around your expected gain/loss. You can get that by summing the expected gain/loss of your two sessions. If a 3 SD negative deviation from that expected loss does not ruin you, then your overall RoR is low.
However, this shows that you cannot simply combine two different plays in one RoR formula. Let us say your cover play is expected to cost you 1000 units and your +EV play is expected to gain you 5000 units. You only have 500 units of bankroll. Clearly, your RoR depend entirely on which order you do the two plays.
link to original post
Thanks, yeah I figured it wasnít that easy.
I understand the concept but could you please give an example from the numbers I gave so I can see better what you mean?
Sorry to bother, but unfortunately Iím a bit slow on these things.
link to original post
$100 for 30 rounds of a -1.5% edge with 1.4 variance
expected loss =100*30*-.015 = -$45
variance = ($100^2)*1.4*30 = 420,000($^2)
$120 for 200 rounds of a +2.5% game with 2.3 variance
expected gain =120*200*.025 = $600
variance = ($120^2)*2.3*200= 6,624,000($^2)
total EV = 600 - 45 = $555
total variance = (6,624,000 + 420,000)($^2)
std dev = sqrt(var) = sqrt(6624000 + 420000) =$2,654
Note that units of variance are dollars squared and units of SD are simple dollars.
Your 3 SD range is (555-(3*2654)) to (555+(3*2654)) so you need a bankroll of $7404 to avoid being busted by any thing less than a 3 SD swing.
Technically, this SD range refers to the final bankroll. There is some chance that you will be down $8000 at some point, but recover to be down only $7000, which puts you within 3 SD of expectation. But, you are still ruined with a $7404 bankroll.
Note that your variance is dominated by the +EV session, not your -EV session. If you used $10 chips as units, then your variance numbers are reduced by a factor of 100 and your SD becomes 265.4 units. The choice of units does not effect the bankroll requirements stated as dollars.
link to original post
Thatís great, thank you for taking the time, now I understand.
How can I use this for ďplay foreverĒ RoR?
Because I guess as I increase the number of rounds the -3sd from the mean is not going to give a usable number anymore, cause it goes too much in the positive, if I get this right?
Also, and I guess here it goes very hard really fast, is it possible to account for a spread?
What I mean is: what if instead of flat betting $100 in the -EV game I were to spread from say 25 to 500, giving an average of $100. That would also affect risk correct? And it wouldnít be the same as calculating it for a flat bet? Meaning calculating risk from the average bet would not work?
link to original post
A double bet gives you four times more variance. A triple bet gives you nine times more variance. These variances add up in the same way.
So, if you play 3000 bets of 2 units with variance 1.0, your overall result has a variance 3000*(2^2)*1.0 = 12000u^2
iI you play 1000 bets of 1, 2 and 3 units with variance 1.0, your overall result has a variance 1000*(1^2)*1.0 + 1000*(2^2)*1.0 +1000*(3^2)*1.0 = 14000u^2. You have increased your variance for the same amount of total action.
Of course, with BJ bet spreading, your small bets will be more numerous than your biggest bets, but the terms of the sum are always the same, number of bet times (units^2) times variance per unit bet.
In the long term, the 3 SD number will still give you an estimate of the range out outcomes for your bankroll. Eventually, even the bottom of that bankroll range will reflect a profit. The 3 SD range is still predictive of your results, but now your RoR is vanishingly small because your deviations are small compared to your final bankroll.
"If you can't explain it simply, you don't understand it well enough." - Albert Einstein
Can you explain this joke in Albert Einsteinís words? More accurately, what is the variance of a blackjack hand if insurance is always taken?
Quote: acesideLet me use Blackjack as an example to understand you. The variance of a main bet is about 1.3 and the variance of an insurance side bet is about 1.9. I often heard players saying that if you take insurance, your overall variance will be lower. I think this is a joke. Or maybe I donít understand this concept very well.
Can you explain this joke in Albert Einsteinís words? More accurately, what is the variance of a blackjack hand if insurance is always taken?
link to original post
The insurance bet is almost perfectly negatively correlated with you main bet. When insurance wins, the main bet loses (or pushes in effect if you take even money on a blackjack). Betting on two negatively correlated bets reduces variance. Think doey dont in craps.
Well, the variance is not affected for any hand where the dealer up card is not an ace, right.Quote: acesideLet me use Blackjack as an example to understand you. The variance of a main bet is about 1.3 and the variance of an insurance side bet is about 1.9. I often heard players saying that if you take insurance, your overall variance will be lower. I think this is a joke. Or maybe I donít understand this concept very well.
Can you explain this joke in Albert Einseinís words?
link to original post
Let us simplify and say you are playing a strategy where you never split or double against an Ace. Also, assume you win 40% of the time you play against an Ace, push 20% of the time, and lose 40% of the time. Ignore when you already have BJ.
Without insurance, the variance of this situation is
(0.40 * 1^2) + (0.2 * 0^2) + (0.4 * -1^2) = 0.8
Now, assume that the Dealer has BJ 20% of the time. This means half your losses are to a dealer BJ, and the rest due to losing the hand normally. With insurance, the variance of this outcomes is
(0.40 * 0^2) + (0.2 * -1^2) + (0.2 * -2^2) + (0.2 * -0^2) = 1.0
So, BJ insurance does not reduce variance under this particular set of assumptions.
In order to reduce variance, insurance needs to be negatively correlated to your most likely outcomes and needs to be sized properly. If you over-insured against any event, you actually increase your variance, even if the insurance acts to offset the loss you are worried about. If your insurance is negatively correlated with only a few outcomes and positively correlated with the rest, then insurance also fails to reduce variance.
In summary, no, I cannot explain it simply.
It is pretty far from perfect negative correlation. You can easily lose the hand and the insurance bet at the same time, and the variance contribution from losing two bets is substantial. I cannot be bothered to calculate the variance using realistic numbers because I simply don't care about BJ insurance. I am sure someone has run the numbers and written about it.Quote: unJonQuote: acesideLet me use Blackjack as an example to understand you. The variance of a main bet is about 1.3 and the variance of an insurance side bet is about 1.9. I often heard players saying that if you take insurance, your overall variance will be lower. I think this is a joke. Or maybe I donít understand this concept very well.
Can you explain this joke in Albert Einsteinís words? More accurately, what is the variance of a blackjack hand if insurance is always taken?
link to original post
The insurance bet is almost perfectly negatively correlated with you main bet. When insurance wins, the main bet loses (or pushes in effect if you take even money on a blackjack). Betting on two negatively correlated bets reduces variance. Think doey dont in craps.
link to original post
To calculate this, we can think of this insurance bet as an opportunity for the player to half down, instead of double down occasionally. For a 6-deck game, the player EV will decrease, but what is the variance now if player takes insurance all the time? Is it less or more than the usual variance number of 1.3 for the main blackjack game?
Quote: MentalIt is pretty far from perfect negative correlation. You can easily lose the hand and the insurance bet at the same time, and the variance contribution from losing two bets is substantial. I cannot be bothered to calculate the variance using realistic numbers because I simply don't care about BJ insurance. I am sure someone has run the numbers and written about it.Quote: unJonQuote: acesideLet me use Blackjack as an example to understand you. The variance of a main bet is about 1.3 and the variance of an insurance side bet is about 1.9. I often heard players saying that if you take insurance, your overall variance will be lower. I think this is a joke. Or maybe I donít understand this concept very well.
Can you explain this joke in Albert Einsteinís words? More accurately, what is the variance of a blackjack hand if insurance is always taken?
link to original post
The insurance bet is almost perfectly negatively correlated with you main bet. When insurance wins, the main bet loses (or pushes in effect if you take even money on a blackjack). Betting on two negatively correlated bets reduces variance. Think doey dont in craps.
link to original post
link to original post
Ok thatís fair.
Quote: Mental
Of course, with BJ bet spreading, your small bets will be more numerous than your biggest bets, but the terms of the sum are always the same, number of bet times (units^2) times variance per unit bet.
link to original post
So taking a CVCX sim as an example, after I put in a 1-16 spread it gives me:
- Avg bet: $80.23
- %W/L: 1.376%
- Win/h: $110.40 (100 rounds/h)
- SD/round: $136.33
- SD/h: $1363.33
- RoR: 0.3% (50k bankroll)
The RoR formula above does very well at estimating RoR since if I plug in the numbers above it gives:
e^((-2*0.01376*(50000/80.23))/(136.33/80.23)^2)= 0.26%
Letís say one plays 1 hour of BJ using the same spread resulting in the same average bet but disregarding count, basically betting randomly (but keeping the same frequency, the same ratio between big and small bets) playing perfect basic strategy but of course a losing game with -0.5% edge.
Then he plays 4 hours of correct counting as per the sim above, for a total of 5 hours of play (and this is repeated forever for RoR purposes)
Is it ok for estimating RoR to use the same SD from the sim above (it changes only slightly for play without indices) but the average edge between +EV time and -EV time?
Avg edge = (($80.23*-0.005*100 rounds)+($80.23*0.01376*400 rounds))/($80.23*500 rounds) = 0.01
So for the RoR formula:
e^((-2*0.01*(50000/80.23))/(136.33/80.23)^2) = 1.33%
Is this an ok ESTIMATE or is it just way off and total nonsense? Like the real answer being something way higher like 20% risk?
Quote: MentalIf your cover play has the same bet spread statistics as your main play, then it will have quite similar variance. I would think that adjusting the EV would give you a decent RoR estimate.
link to original post
Thank you very much, good to hear Iím not totally crazy
Quote: MentalWell, the variance is not affected for any hand where the dealer up card is not an ace, right.Quote: acesideLet me use Blackjack as an example to understand you. The variance of a main bet is about 1.3 and the variance of an insurance side bet is about 1.9. I often heard players saying that if you take insurance, your overall variance will be lower. I think this is a joke. Or maybe I donít understand this concept very well.
Can you explain this joke in Albert Einseinís words?
link to original post
Let us simplify and say you are playing a strategy where you never split or double against an Ace. Also, assume you win 40% of the time you play against an Ace, push 20% of the time, and lose 40% of the time. Ignore when you already have BJ.
Without insurance, the variance of this situation is
(0.40 * 1^2) + (0.2 * 0^2) + (0.4 * -1^2) = 0.8
Now, assume that the Dealer has BJ 20% of the time. This means half your losses are to a dealer BJ, and the rest due to losing the hand normally. With insurance, the variance of this outcomes is
(0.40 * 0^2) + (0.2 * -1^2) + (0.2 * -2^2) + (0.2 * -0^2) = 1.0
So, BJ insurance does not reduce variance under this particular set of assumptions.
In order to reduce variance, insurance needs to be negatively correlated to your most likely outcomes and needs to be sized properly. If you over-insured against any event, you actually increase your variance, even if the insurance acts to offset the loss you are worried about. If your insurance is negatively correlated with only a few outcomes and positively correlated with the rest, then insurance also fails to reduce variance.
In summary, no, I cannot explain it simply.
link to original post
I didnít read into this part yesterday. Now, I find I still donít understand your second equation above,
Quote: ďWith insurance, the variance of this outcomes is
(0.40 * 0^2) + (0.2 * -1^2) + (0.2 * -2^2) + (0.2 * -0^2) = 1.0.Ē
As you described, when the dealer shows an Ace, the player will always take insurance, and the EV in your specific example will be EV=0. However, have you taken into account the fact that the insurance side bet amount is restricted to only 0.5 unit bet?
If you could list all possible outcomes of your example, that would great! The ultimate part that confuses me is this question, are the blackjack main bet and the insurance side bet really correlated? I guess no.
No, I wasn't even aware that the insurance bet was limited to half the main bet.Quote: acesideQuote: MentalWell, the variance is not affected for any hand where the dealer up card is not an ace, right.Quote: acesideLet me use Blackjack as an example to understand you. The variance of a main bet is about 1.3 and the variance of an insurance side bet is about 1.9. I often heard players saying that if you take insurance, your overall variance will be lower. I think this is a joke. Or maybe I donít understand this concept very well.
Can you explain this joke in Albert Einseinís words?
link to original post
Let us simplify and say you are playing a strategy where you never split or double against an Ace. Also, assume you win 40% of the time you play against an Ace, push 20% of the time, and lose 40% of the time. Ignore when you already have BJ.
Without insurance, the variance of this situation is
(0.40 * 1^2) + (0.2 * 0^2) + (0.4 * -1^2) = 0.8
Now, assume that the Dealer has BJ 20% of the time. This means half your losses are to a dealer BJ, and the rest due to losing the hand normally. With insurance, the variance of this outcomes is
(0.40 * 0^2) + (0.2 * -1^2) + (0.2 * -2^2) + (0.2 * -0^2) = 1.0
So, BJ insurance does not reduce variance under this particular set of assumptions.
In order to reduce variance, insurance needs to be negatively correlated to your most likely outcomes and needs to be sized properly. If you over-insured against any event, you actually increase your variance, even if the insurance acts to offset the loss you are worried about. If your insurance is negatively correlated with only a few outcomes and positively correlated with the rest, then insurance also fails to reduce variance.
In summary, no, I cannot explain it simply.
link to original post
I didnít read into this part yesterday. Now, I find I still donít understand your second equation above,
Quote: ďWith insurance, the variance of this outcomes is
(0.40 * 0^2) + (0.2 * -1^2) + (0.2 * -2^2) + (0.2 * -0^2) = 1.0.Ē
As you described, when the dealer shows an Ace, the player will always take insurance, and the EV in your specific example will be EV=0. However, have you taken into account the fact that the insurance side bet amount is restricted to only 0.5 unit bet?
If you could list all possible outcomes of your example, that would great! The ultimate part that confuses me is this question, are the blackjack main bet and the insurance side bet really correlated? I guess no.
link to original post
"What is insurance in blackjack? Blackjack insurance is a side bet offered to the player if the dealer's up-card is an ace, as insurance against the dealer's hand being 'blackjack'. Blackjack insurance odds pay out at 2/1 and the maximum bet allowed is generally half of the player's main bet."
I was also confused about the whether the payout was 2 to 1 or 2 for 1.
My math was just an example of how you could actually increase you variance by insuring under specific circumstances. My assumptions apparently are very far from the real conditions regarding insurance. I have never taken an insurance bet, and I never had much interest in the math. Sorry if I mislead or confused anyone.
The main bet and the insurance bet are always anticorrelated when the dealer has blackjack and the player does not. The rest of the time, it is a mixed bag. If the player has a hard total of 16, then a losing insurance bet is positively correlated with a losing main bet.
But the whole idea of choosing to gamble and then choosing to make an extra bad -EV bet to reduce variance is really stupid in the first place. The more effective way to reduce variance is to reduce the main bet.
However, we can calculate this by thinking of an insurance bet as an opportunity for the player to half down (instead of double down occasionally) to find a total variance number. It may go up or down, but the cost of playing insurance is huge though. We can not compare variances when their respective EV numbers are significantly different.
You can only add the variances of two uncorrelated wagers if you want to get the variance of the sum of the outcomes. In this case, the two wagers are clearly partially correlated, and therefore not independent events.Quote: acesideThank you for clarifying this! Regarding the main-insurance correlation, I have had this same discussion with Don on another site. I still insist that these two are independent and their math calculations are independent too.
However, we can calculate this by thinking of an insurance bet as an opportunity for the player to half down (instead of double down occasionally) to find a total variance number. It may go up or down, but the cost of playing insurance is huge though. We can not compare variances when their respective EV numbers are significantly different.
link to original post
What if I insured your entire BJ hand for free? If you win, you pay me the profit, but if you lose, I pay you back your loss.
My offer to insure you has exactly the same variance as your play. Now you have twice the variance by your line of reasoning because you have two stochastic processes going on at once, both with variance 1.3. Yet, your variance has gone to zero.
Things would be different if I insured you against the wager of another player playing the same game at the same stakes at another table, because correlation between your hand and the insured wager is nil.
The second column in the table is the number of ways the dealer can receive two cards in the first column in that order. The other columns list the number of ways that the player can get the two cards at the top of the column given that the dealer has already taken the two cards at the left. The total of the table is 1512 = 9 * 8 * (7choose2) ways.
TT 99 9T AT A9
A9 4 24 12 48 0 0
AT 4 12 24 48 0 0
9A 4 24 12 48 0 0
TA 4 12 24 48 0 0
TT 12 12 72 96 24 48
99 12 72 12 96 48 24
9T 16 48 48 144 48 48
T9 16 48 48 144 48 48
552 ways are losers, 408 are pushes, 384 are winners, and 168 ways result in a player 21, which is never a push. I calculate the variance as 0.869047619. It is a simple matter to recalculate the variance under any insurance scheme. For example, you could use standard rules or you could allow insuring against BJ for a full bet, and insurance pays off at 1:1.
Some insurance schemes will increase variance, others will decrease it. You can set up a spreadsheet to do the whole variance recalculation and play around with it. One thing is clear, you cannot get the variance of the game by calculating the variance of the insurance bet and the main game separately without calculating the covariance.
1. When Insurance is not allowed,
EV=0.0556;
Variance=0.8660.
2. When Insurance pays 1 to 0.5 unit (only) bet.
EV=0.0833;
Variance=0.8609.
3. When Insurance pays 1 to 1 unit (only) bet.
EV=0.0556;
Variance=0.9453.
This means that variance increases sometimes but decreases some other times. Another thought of mine: although this mini-Blackjack uses a 9-card single deck, can we use an infinite 9-card deck to achieve the same goal?
Quote: acesideYour mini-Blackjack game is very creative! Assuming your game pays 3 to 2 on a player's blackjack, I get these 3 sets of EV and variance numbers:
1. When Insurance is not allowed,
EV=0.0556;
Variance=0.8660.
2. When Insurance pays 1 to 0.5 unit (only) bet.
EV=0.0833;
Variance=0.8609.
3. When Insurance pays 1 to 1 unit (only) bet.
EV=0.0556;
Variance=0.9453.
This means that variance increases sometimes but decreases some other times. Another thought of mine: although this mini-Blackjack uses a 9-card single deck, can we use an infinite 9-card deck to achieve the same goal?
link to original post
The calculation is a bit more complex with an infinite 9-card deck because you can have AT versus AT whereas this never happens with a 9-card deck. But the 9-card deck has big removal effects that distort the results. I would be interested in your results if you do the infinite 9-card calculation.
I have some slight disagreements with your calculation results. I did six calculations using different insurance rules with the same spreadsheet. I have a checksum to be sure my counts add up to 1512, but I could still have an error in my spreadsheet.
In my results, normal insurance barely reduces the variance for this simplified game. Over-insuring actually increases variance substantially. All insurance adds EV because there are a lot of insurance payoffs when your hand is 99. This won't be such a big effect in the real BJ game (smaller card removal effects). I suspect that taking insurance barely changes variance in a real BJ game.
Insurance 0 pays 0
EV= 0.0556
Variance= 0.8690
Insurance 0.5 pays 1.5
EV= 0.0833
Variance= 0.8671
Insurance 1 pays 2
EV= 0.1349
Variance= 0.9484
Insurance 1 pays 3
EV= 0.1905
Variance= 1.0040
Insurance 2 pays 4
EV= 0.2063
Variance= 1.2500
Insurance 2 pays 6
EV= 0.1508
Variance= 1.6944
1. When Insurance is not allowed, play main game only:
EV=0.0556;
Variance=v1.
2. When both main and insurance are allowed, play both:
EV=0.0833;
Variance=v2.
3. When main bet is not allowed, play Insurance only:
EV=ev3
Variance=v3.
Can you help calculate these above numbers? And based on these, find a co-variance number between main and insurance?
Thanks
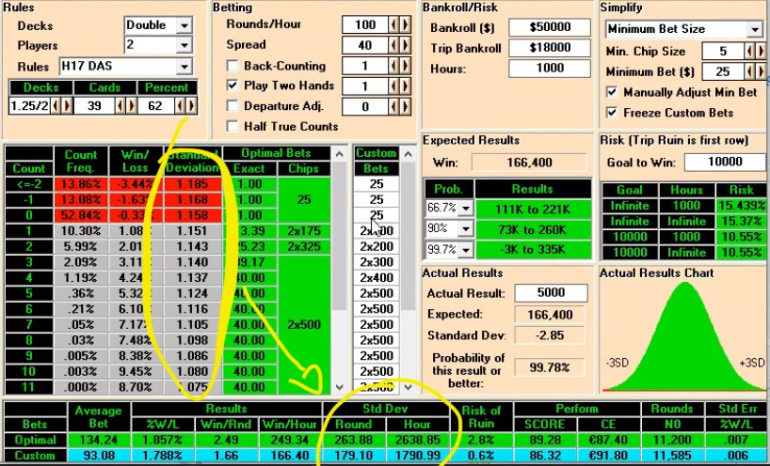
Quote: gunbjCan someone please explain to me in the simulation example below how to get from the individual standard deviation numbers listed in the count columns to the total standard deviation per round and per hour?
link to original post
Nevermind, I was surprisingly able to do this myself in Excel:
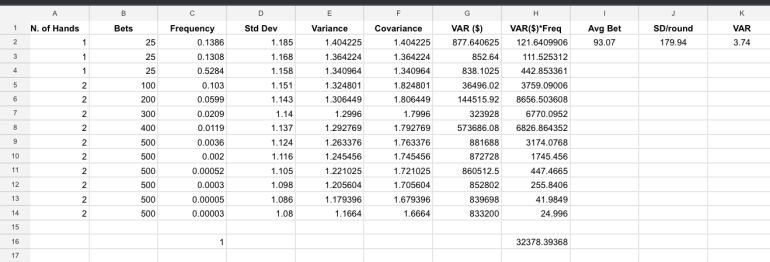
But in order to arrive at the same numbers as in the simulation above I had to calculate the variance according to bet frequency, basically doing an average of all the variance data of each bet, which is what Mental suggested is not correct, if I understand properly:
Quote: MentalVariance per wager is not germane to risk management. Your total variance for the series of wagers is the important factor. The average is not.
link to original post
So if CVCX can take various bets of different edges and standard deviations to find a total average variance number to then find RoR, why canít I? 😆
Or am I missing something?
I think I understand the point of confusion here. Maybe I didn't not explain a subtle difference well enough.Quote: gunbjQuote: gunbjCan someone please explain to me in the simulation example below how to get from the individual standard deviation numbers listed in the count columns to the total standard deviation per round and per hour?
link to original post
Nevermind, I was surprisingly able to do this myself in Excel:
But in order to arrive at the same numbers as in the simulation above I had to calculate the variance according to bet frequency, basically doing an average of all the variance data of each bet, which is what Mental suggested is not correct, if I understand properly:Quote: MentalVariance per wager is not germane to risk management. Your total variance for the series of wagers is the important factor. The average is not.
link to original post
So if CVCX can take various bets of different edges and standard deviations to find a total average variance number to then find RoR, why canít I? 😆
Or am I missing something?
link to original post
Let me pose a very simple variance problem and see if this helps.
I play a game with variance 3.0. Exactly 20% of the time, on average, the game flips to +EV mode and I bet 2 units instead of 1. There is no correlation between consecutive games. So, the average variance of one game is:
3*0.8 + 9*0.2 = 4.2
This use of an average is meaningful in this case because the ratio of the number of 1-unit game to 2-unit games is fixed at 4:1. If I play 1000 games, I expect to play 800 1-unit games (variance=2400) and 200 2-unit games (variance=1800). The total variance = 4200, so you could have obtained the total variance by multiplying the average variance/game by 1000.
Now, consider a different calculation. You want to know the total variance for N 1-unit games and M 2-unit games, where there is no fixed ratio between M and N. The formula is N*3 + M*9. You could divide this total variance by (N+M) and get an average variance. Then you could multiply by (N+M) to get the total variance. But you already had that number, so that extra step doesn't help at all. This is what I meant by saying the average is not generally meaningful. For any particular ratio of N:M, you will get a different average variance.
In your simulation, the ratios of the different bet sizes are fixed by the count frequency generated by the counting system. For a given counting system, then, you can use an average variance/game. What you are doing in your spreadsheet is calculating that average, and it is a meaningful number for that particular counting system. But you got that average by totaling the weighted variances of the different bets the proper way.
Unlike my hypothetical game, your hands are correlated: you are not going to go from min bet to max bet and back again in three hands. Therefore, you are going to have long runs of hand with low variance and short runs of hands with high variance. The average variance is only meaningful over many shoes.
I hope this helps clarify my previous comments.
Particularly, the problem is this: if we look at the insurance bet only without main bet at all, its EV and variance numbers will be different from these from the combination 0 bet on main and 0.5 bet on insurance. This is my headache. Thank you for your help!
Calculating the covariance is time consuming. I personally try to avoid doing it if I can just estimate or calculate the variance directly. I am not going to do the calculation here, because I don't have any reason to care about the insurance bet.Quote: acesideHi Mental, I will calculate out the EV and variance numbers for the mini-Blackjack game myself soon. However, I still havenít thought through how to calculate the co-variance number between the main bet and the the insurance bet. The main problem is these two bets are independent sometimes, but may correlate other times. This part bothers me.
Particularly, the problem is this: if we look at the insurance bet only without main bet at all, its EV and variance numbers will be different from these from the combination 0 bet on main and 0.5 bet on insurance. This is my headache. Thank you for your help!
link to original post
Yes, there is zero covariance when the dealer does not have an ace showing.
Var(aX+bY)=a^2Var(X)+b^2Var(Y)+2abCov(X,Y)
Whenever Cov(X,Y) is zero the last term can be ignored Var(aX+bY)=a^2Var(X)+b^2Var(Y). This is just like adding independent variables. When the dealer has an ace up, you need to use the covariance. Then, you need to weight the variance for the different situations and sum to get the total variance.
if a=0, only the middle term is non-zero and the other terms can be ignored, etc. So if X is the main bet, and you bet zero on the main bet and 0.5 on the insurance bet, then a=0 and b=0.5, then the variance = Var(0*X+0.5*Y) = 0.5*Var(Y). No need to worry about covariance.
Quote: Mental
I hope this helps clarify my previous comments.
link to original post
If it doesnít itís probably not your fault 😅
But I think I am understanding what you are saying.
Taking your example, I should be able to apply this to my problem of the two games, right?
So, in light of this, my question is:
Say I take the simulation and spreadsheet above as my ďcorrect playĒ which I play for 5 hours.
Then I go onto play a a negative game that I can play for 1 hour.
EDIT: I suspect there might be some confusion here, I think I didnít explain myself properly. This cycle of 1-5 hours of play is not a one-off event, itís to be repeated indefinitely, thatís why I think this is applicable, since as you said:
Quote: Mental
The average variance is only meaningful over many shoes.
So I made a spreadsheet to work out the variance data from a set spread that I decide to use on the negative game (std dev data is from a simulation).

The spreadsheet shows that for this game, with this kind of spread the variance is 2.05
Now calculate the total variance for each game:
Avg bet of 1st game ^2 * variance of the 1st game:
93.08^2 * 3.74 = 32,402.94
Avg bet of the 2nd game ^2 * variance of the 2nd game:
135^2 * 2.05 = 37,361.25
Now I weigh the two variances according to the ratio, or frequency of the games played:
(Total variance of 1st game * (rounds of 1st game /(rounds of the 1st game + rounds of the 2nd game):
32,402.94 * (500/(500+100)) = 27,002.45
(Total variance of 2nd game * (rounds of 2nd game /(rounds of the 1st game + rounds of the 2nd game):
37,361.25 * (100/(500+100)) = 6,226.87
I add them together:
6,226.87 + 27,337.50 = 33,564.37
To find SD/round:
Sqrt(33,564.37) = $183.21
Before I can calculate final variance per wager I have to find out the average bet between the two games so I weigh that:
(93.08*(500/(500+100)))+(135*(100/(500+100)))= 100.07
So finally to calculate combined variance per wager:
(SD/round / Avg bet)^2:
(178.59 / 100.07)^2 = 3.3517
Before I can find RoR I have to find the average edge of the two games combined:
1st game EV/h: $166.43 * 5 hours = $832.15
2nd game EV/h: -$97.20 * 1 hour = -$97.20
832.15 - 97.20 = $734.95
To find average edge:
Total EV / (Avg bet * total rounds):
734.95 / (100.07 * 600) = 0.0122
So now for the total RoR (50k bankroll):
EXP((-2*0.0122*(50000/100.07))/3.3517) = 2.63%
Is this all wrong?
Quote: gunbjQuote: Mental
I hope this helps clarify my previous comments.
link to original post
If it doesnít itís probably not your fault 😅
But I think I am understanding what you are saying.
Taking your example, I should be able to apply this to my problem of the two games, right?
So, in light of this, my question is:
Say I take the simulation and spreadsheet above as my ďcorrect playĒ which I play for 5 hours.
Then I go onto play a a negative game that I can play for 1 hour.
EDIT: I suspect there might be some confusion here, I think I didnít explain myself properly. This cycle of 1-5 hours of play is not a one-off event, itís to be repeated indefinitely, thatís why I think this is applicable, since as you said:Quote: Mental
The average variance is only meaningful over many shoes.
link to original post
Perhaps I should not have confused the issue by making the last statement. Before you start a shoe, you only know what the expected variance per hand will be. After the shoe is complete, you have new information. You know how many hands you actually played at each bet level. You can calculate the variance that that particular shoe inflicted on you. I could be higher or lower than a typical shoe. This will average out over many shoes.
If you always have the same ratio of +EV hands and cover hands in each cycle, then you can use your average variance per hand in your RoR calculations. Let us say a cycle is 300+60 hands with a total variance of V and an average variance of v = V/360. Now, if you play seven cycles, you get the same total variance if you calculate it as 7*V or 7*360*v, right? Your RoR calculations should give the right result if you use v.
Quote: Mental
If you always have the same ratio of +EV hands and cover hands in each cycle, then you can use your average variance per hand in your RoR calculations.
Ok great, yes that it the case here, Iím sorry if that wasnít clear.
Quote: MentalLet us say a cycle is 300+60 hands with a total variance of V and an average variance of v = V/360. Now, if you play seven cycles, you get the same total variance if you calculate it as 7*V or 7*360*v, right? Your RoR calculations should give the right result if you use v.
link to original post
Yes, great, I think we are very close to the solution.
Could you please show what you mean by total variance V and average variance v using the numbers in my example above?
Because here Iím probably making confusion and ending up with different numbers when I multiply the variance in the way you described, so Iím probably still not using the right number.
Iím very close to stopping bothering you 😅
Quote: gunbjQuote: Mental
If you always have the same ratio of +EV hands and cover hands in each cycle, then you can use your average variance per hand in your RoR calculations.
Ok great, yes that it the case here, Iím sorry if that wasnít clear.Quote: MentalLet us say a cycle is 300+60 hands with a total variance of V and an average variance of v = V/360. Now, if you play seven cycles, you get the same total variance if you calculate it as 7*V or 7*360*v, right? Your RoR calculations should give the right result if you use v.
link to original post
Yes, great, I think we are very close to the solution.
Could you please show what you mean by total variance V and average variance v using the numbers in my example above?
Because here Iím probably making confusion and ending up with different numbers when I multiply the variance in the way you described, so Iím probably still not using the right number.
Iím very close to stopping bothering you 😅
link to original post
I did the calculation a different way than you, and I get essentially the same answers. I am just dividing the total variance by 600 to get and average variance, rather than doing the weighted sum as you did.
So, I am saying you could just get an average EV per round like you suggested in the original post and you would get a good set of numbers to use in your RoR formula.
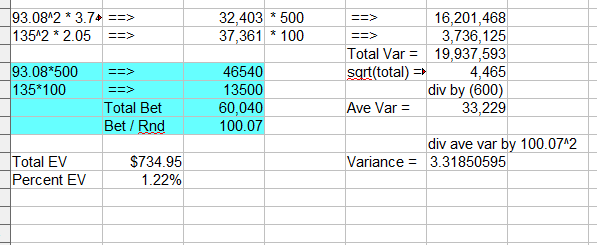
93.08^2 * 3.74 ==> 32,403 * 500 ==> 16,201,468
135^2 * 2.05 ==> 37,361 * 100 ==> 3,736,125
Total Var = 19,937,593
93.08*500 ==> 46540 sqrt(total) = 4,465
135*100 ==> 13500 div by (600)
Total Bet 60,040 Ave Var = 33,229
Bet / Rnd 100.07
div ave var by 100.07^2
Total EV $734.95 Variance = 3.3185059452
Percent EV 1.22%
Your RoR formula is a useful approximation based on the central limit theorem. Gaussian distributions have exponential tails, and your formula uses the integral of the gaussian tail to find out how likely it is that this tail risk exceeds your bankroll. The formula should be a good approximation for wagers with modest variance like BJ. But the approximation breaks down when your entire bankroll is a small number of bets. Your bankroll is dozens of bets, so you should be okay.
Over the years, I have done hundreds of simulations of W/L distributions for loss rebates. For loss rebate promotions, you are often betting 10%, 50%, even 100% of your bankroll on a single wager (for this purpose, your bankroll is the promo loss limit). I cannot optimize loss rebates by using a simple RoR formula. This is especially true because I deliberately seek out high variance slots or VP to play the loss rebate. I have always gone directly to Monte Carlo simulations for guidance. MC sims are valuable tool to have in your toolkit.
Quote: MentalQuote: gunbjQuote: Mental
If you always have the same ratio of +EV hands and cover hands in each cycle, then you can use your average variance per hand in your RoR calculations.
Ok great, yes that it the case here, Iím sorry if that wasnít clear.Quote: MentalLet us say a cycle is 300+60 hands with a total variance of V and an average variance of v = V/360. Now, if you play seven cycles, you get the same total variance if you calculate it as 7*V or 7*360*v, right? Your RoR calculations should give the right result if you use v.
link to original post
Yes, great, I think we are very close to the solution.
Could you please show what you mean by total variance V and average variance v using the numbers in my example above?
Because here Iím probably making confusion and ending up with different numbers when I multiply the variance in the way you described, so Iím probably still not using the right number.
Iím very close to stopping bothering you 😅
link to original post
I did the calculation a different way than you, and I get essentially the same answers. I am just dividing the total variance by 600 to get and average variance, rather than doing the weighted sum as you did.
So, I am saying you could just get an average EV per round like you suggested in the original post and you would get a good set of numbers to use in your RoR formula.93.08^2 * 3.74 ==> 32,403 * 500 ==> 16,201,468
135^2 * 2.05 ==> 37,361 * 100 ==> 3,736,125
Total Var = 19,937,593
93.08*500 ==> 46540 sqrt(total) = 4,465
135*100 ==> 13500 div by (600)
Total Bet 60,040 Ave Var = 33,229
Bet / Rnd 100.07
div ave var by 100.07^2
Total EV $734.95 Variance = 3.3185059452
Percent EV 1.22%
Your RoR formula is a useful approximation based on the central limit theorem. Gaussian distributions have exponential tails, and your formula uses the integral of the gaussian tail to find out how likely it is that this tail risk exceeds your bankroll. The formula should be a good approximation for wagers with modest variance like BJ. But the approximation breaks down when your entire bankroll is a small number of bets. Your bankroll is dozens of bets, so you should be okay.
Over the years, I have done hundreds of simulations of W/L distributions for loss rebates. For loss rebate promotions, you are often betting 10%, 50%, even 100% of your bankroll on a single wager (for this purpose, your bankroll is the promo loss limit). I cannot optimize loss rebates by using a simple RoR formula. This is especially true because I deliberately seek out high variance slots or VP to play the loss rebate. I have always gone directly to Monte Carlo simulations for guidance. MC sims are valuable tool to have in your toolkit.
link to original post
Great, thanks!


