Probability of 35 wins in 100 hands (Baccarat)

Hello world! I was wondering what are the chances (probability) of getting 35 wins or less in 100 hands of baccarat (excluding draws) and how do I calculate this in general with a different number of hands played and even different expected winrates. Let's say I'll play 60 hands and win 21 of them (wich is the same 35% winrate), wich I think it can happen more often than winning just 350 hands in 1000 hands played. How do I calculate this with a general formula and different number of hands played? Let's just pretend the winning change is 50% because I don't care about the return of 0.95 from the banker because I'm playing randomly on banker and player. Another problem is that I don't really understand the concept of standard deviation and variance. I understand that baccarat has a low variance but in the case of a 35% winrate it is pretty volatile and I wish I could calculate the chances to get 35% winrate in a such low-volatility game. Thanks!

Coin Tossing

Let's approach this differently and consider the simple game of tossing a coin, this should help with variance.
If we toss a coin four times it could end up with between 0 and 4 heads, with probabilities 0:1/16 1:4/16 2:6/16 3:4/16 4:1/16. These numbers can be deduced from the following idea (to create an entry add the two numbers in the row above)...

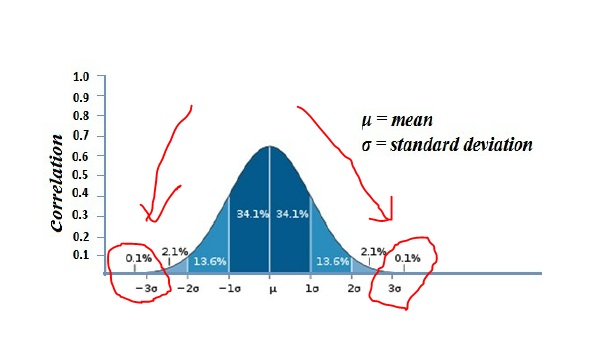
Obviously the average number of heads will be half, but occasionally the result will be somewhat different. At ten coins, see last row, the average is 5 heads (underlined) but it's also reasonably likely you'll get somewhere between 3 and 7 (912 ways) and less likely to get 0-2 (56 ways) or 8-10 (56 ways).
Another way of putting it is there is a 90% chance of getting 3-7, 5% 0-2, so it's 95% that we'll get 3 or more heads.

The mathematical formula is the average will be Np (N=number of tosses, p=chances of correct result), the Standard Deviation is SQRT(Npq) (q=1-p=chances of wrong result). So for N=10, Average=5, SD=1.58 (SQRT(10*.5*.5)).

There are now tables which explain (see "normal distribution") how likely results lie within various SDs, so we can check the "3 or more heads". Average = 5, 2SDs = 3.16, so typically 95% of results will be greater than 2.

Making Pencils
Here's an easier example in real life, we're making pencils, filling bottles of pop, whatever it is the customer expects the pencil to be 8" (or longer), the bottle of pop 500ml (or more). However the machine isn't perfect so we should establish the average length of pencils produced given how much accuracy our machine can make. Our objective is to ensure 95% of pencils are 8" or longer. (The maths will tell us for a given machine accuracy, how much longer we should set the average size of pencils.)

The accuracy corresponds to the SDs, so if the machine is extremely good we might be able to set the average pencil 8.05", otherwise we might have to set it longer. The trade-off is paying for a more accurate machine or accept higher production costs to make slightly longer pencils to ensure 95% are 8". In practice no-one is going to complain about a long pencil, but what if we're making nuts and bolts, they have to be accurate enough to fit together. Therefore we would invest in a much better machine.

I understand you probably have reasons for choosing 35 wins and 100 hands. Since you appear not to care about data per "shoe" of data, each around 80 hands, I won't. But, I'd be interested in knowing why 35-in-100, rather than something like 25-per-shoe.

I like the WoO baccarat simulation data, located here. If you download the ten data files as raw text, you can get a lot of data to play with. Remove the Wizard's summary at the end of each file, the commas, the digits, and the Ts (for Ties, which you said to ignore). You are left with 10 data files containing only Bs and Ps. Copy them into a database or a worksheet, each with a unique, sequential ID number.

Now, use a random number generator (or any system you choose) to pick a starting place in your data. For example, suppose you start at row 4321, shown as "P". Have a column for Ps and a column for Bs, and count the next 100 results. (True, the next 100 rows of data may not come from the same shoe, with possible unintended effects. Noted, but we're also not really playing baccarat in this reply.) Now, if you're jumping between B and P bets as you try to connect with the next winner, that methodology would have to be included somehow. Rinse and repeat...

I hope this is helpful. Good luck.

Quote: Sacke86

Hello world! I was wondering what are the chances (probability) of getting 35 wins or less in 100 hands of baccarat (excluding draws) and how do I calculate this in general with a different number of hands played and even different expected winrates. Let's say I'll play 60 hands and win 21 of them (wich is the same 35% winrate), wich I think it can happen more often than winning just 350 hands in 1000 hands played. How do I calculate this with a general formula and different number of hands played?
link to original post

There is no "universal formula" to do this.
I can think of two ways to calculate them; note that the first one requires a spreadsheet.

First, "the long way."
If p is the probability of winning (in this case, if you are ignoring ties, p = 0.493176), the probably of having exactly W wins in N hands is C(N,W) * p^W * (1-p)^(N-W).
You need to calculate this for N = 100 and W = 0, 1, 2, ..., 35, then add up those 36 numbers to get 0.00269581, or about 1 / 371.

Second, using statistical approximation.
As Charlie pointed out, the standard deviation for the number of wins in N hands with probability p is sqrt(N p (1-p)).
For 100 hands, this is 4.99953.
Now, for 35 wins, calculate the "Z-score," which is how many standard deviations the value is from the mean value. The mean value is 100 p = 49.3176, so z = (35 - 49.3176) / 4.999953 = about -2.8638.
Unfortunately, there's no magic formula to convert a z-score to a probability (the value is an integral, and nobody has been able to find a way to "simplify" it, so you need to use approximation methods). There are a number of z-tables online (here is one); -2.86 converts to a probability of 0.0021.

Wait a minute...0.00269581 corresponds to a z-score of -2.78.
Anybody out there know if I'm missing something?

There's another way, which gets the same answer, and that is do my earlier method but when adding multiply the left hand side by Pr(Miss) and right by Pr(Hit).

I think the reason the NPQ method doesn't work is because the curve is slightly skewed, also 35 or less includes 35. You can see the probability for 34 is 0.0014, so 0.0021 would suggest somewhere between 34 and 35. If P=.5 then 50 or less is 0.539795 not 0.5.
Continue until 101 rows (row 1 = no games, row 100 = 100 games). Then add them up...

0	0.000 000 000 000
15	0.000 000 000 001
20	0.000 000 001 265
25	0.000 000 559 532
30	0.000 068 377 529
31	0.000 155 449 769
32	0.000 338 143 478
33	0.000 704 465 753
34	0.001 406 897 246
35	0.002 695 813 283
36	0.004 960 354 581
37	0.008 771 918 935
38	0.014 920 925 707
39	0.024 433 034 646
40	0.038 548 377 157
41	0.058 648 725 145
42	0.086 124 570 237
43	0.122 187 031 073
44	0.167 646 284 571
45	0.222 694 415 106
46	0.286 740 442 119
47	0.358 343 712 370
48	0.435 276 638 614
49	0.514 721 219 277
50	0.593 572 583 306
55	0.891 935 858 249
60	0.987 532 318 163
65	0.999 440 573 957
70	0.999 991 166 316
75	0.999 999 956 406
80	0.999 999 999 943
85	1.000 000 000 000
100	1.000 000 000 000

Quote: ThatDonGuy

Second, using statistical approximation.
As Charlie pointed out, the standard deviation for the number of wins in N hands with probability p is sqrt(N p (1-p)).
For 100 hands, this is 4.99953.
Now, for 35 wins, calculate the "Z-score," which is how many standard deviations the value is from the mean value. The mean value is 100 p = 49.3176, so z = (35 - 49.3176) / 4.999953 = about -2.8638.
Unfortunately, there's no magic formula to convert a z-score to a probability (the value is an integral, and nobody has been able to find a way to "simplify" it, so you need to use approximation methods). There are a number of z-tables online (here is one); -2.86 converts to a probability of 0.0021.

Wait a minute...0.00269581 corresponds to a z-score of -2.78.
Anybody out there know if I'm missing something?
link to original post

I think you should use 35.5 instead of 35 since, in a continuous distribution, the probability of getting 35 wins is given by the probability of getting between 34.5 and 35.5. So (35.5 - 49.3176) / 4.999953 = about -2.7638 which corresponds to a probability of 0.00286. This is much closer (within 6% relative) to the exact answer.

Though there's nothing wrong with using a z-table to interpolate the answer, you can easily get the exact probability (based on the normal distribution) using NORM.DIST in Excel or by using an integral calculator to take the integral from negative infinity to -2.7638 of (2*pi)^-.5*e^(-.5x^2) dx. That's probably what Excel does anyway

OK, so for 100 hand we have a SD = SQRT(100*0.5*0.5) = 5? So -5 to 5 wins more lays between -1 and 1 SD and have a probability of 68.2%? Now 35 wins in 100 hands means that we have 15 less wins than the mean of 50, wich is -3SD as 1SD = 5. As I see from these normal distribution graphs this has a probability of 0.2% to have 15 wins more or less in 100 hands, so I can expect to face series or situations like this on average at the starting of every 500th hand (100 / 0.2 = 500) and should be within the math laws? I know it could get worse because of variation but that's the average, I guess. Am I missing something? Sorry for my bad english.

Quote: ThatDonGuy

Quote: Sacke86

Hello world! I was wondering what are the chances (probability) of getting 35 wins or less in 100 hands of baccarat (excluding draws) and how do I calculate this in general with a different number of hands played and even different expected winrates. Let's say I'll play 60 hands and win 21 of them (wich is the same 35% winrate), wich I think it can happen more often than winning just 350 hands in 1000 hands played. How do I calculate this with a general formula and different number of hands played?
link to original post

There is no "universal formula" to do this.
I can think of two ways to calculate them; note that the first one requires a spreadsheet.

First, "the long way."
If p is the probability of winning (in this case, if you are ignoring ties, p = 0.493176), the probably of having exactly W wins in N hands is C(N,W) * p^W * (1-p)^(N-W).
You need to calculate this for N = 100 and W = 0, 1, 2, ..., 35, then add up those 36 numbers to get 0.00269581, or about 1 / 371.

Second, using statistical approximation.
As Charlie pointed out, the standard deviation for the number of wins in N hands with probability p is sqrt(N p (1-p)).
For 100 hands, this is 4.99953.
Now, for 35 wins, calculate the "Z-score," which is how many standard deviations the value is from the mean value. The mean value is 100 p = 49.3176, so z = (35 - 49.3176) / 4.999953 = about -2.8638.
Unfortunately, there's no magic formula to convert a z-score to a probability (the value is an integral, and nobody has been able to find a way to "simplify" it, so you need to use approximation methods). There are a number of z-tables online (here is one); -2.86 converts to a probability of 0.0021.

Wait a minute...0.00269581 corresponds to a z-score of -2.78.
Anybody out there know if I'm missing something?
link to original post

The "long way" could get a lot shorter with a program I've written in Python and I can make it work as a general program with different inputs. Thanks for the formula, by the way! :*

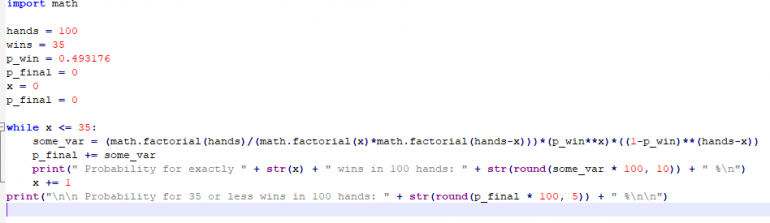
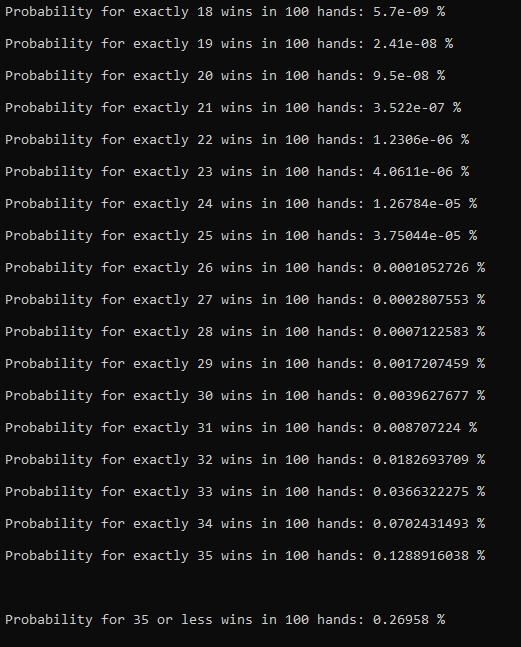
I will investigate that "Z-score" thing too but I think this "long way" is enough for me for the moment :))

Quote: Sacke86

I will investigate that "z-score" thing too but I think this "long way" is enough for me for the moment :))
link to original post

In a way, you already did "investigate the z-score thing" in your previous post. "z-score" is just how many standard deviations away you are from the mean (negative if it is less than the mean, and positive if it is greater). All of the "z-score tables" I have seen convert this number to a probability that the event happens fewer times than that.

For example, given the example with mean = 50 and SD = 5, 35 is a z-score of -3, which converts to a probability of 0.0013, which is (about) the probability of getting fewer than 35 heads in 100 coin flips.

Do you think there's any progressive betting strategy that can go through 35% or lower winrates without going broke? I know l'Abouchere needs winrates as low as 33.3% but bets skyrockets quickly in case of losing series and in case of a win you still remain with big bets and headaches if your unit is more that 1% of your bankroll. I want to find a slow and steady strategy but math beats me and I don't think I can win over the long run without using extremly low units compared with the bankroll, wich then became useless because I don't have $10.000 to use starting bets of just $1. I would be happy if I could win $50 guaranteed in let's say 500 hands and $1000 bankroll with almost no chance to go broke. And even if I'll lose 65% of the hands I would be happy to break-even...

No...

Quote: Sacke86

Do you think there's any progressive betting strategy that can go through 35% or lower winrates without going broke? I know l'Abouchere needs winrates as low as 33.3%

For that matter, a 10-step Martingale on a single-zero roulette wheel only "needs a winrate" of 1/784.

The lower the necessary win rate, the higher the potential loss to potential win ratio becomes.

If you could win $50 "guaranteed" in 500 hands, then you could win $5000 by betting 100 times as much. It wouldn't take that long for this "secret" to get out, and then every casino in the world would go broke.

Repeat after me:
There is no such thing as a sure thing. That's why it's called "gambling."
(Well, unless you count the main event of the first WrestleMania, but (a) you have to go back in time to 1985, and (b) you have to find anyone who was taking bets on professional wrestling at the time.)

Quote: ThatDonGuy

Quote: Sacke86

Do you think there's any progressive betting strategy that can go through 35% or lower winrates without going broke? I know l'Abouchere needs winrates as low as 33.3%

For that matter, a 10-step Martingale on a single-zero roulette wheel only "needs a winrate" of 1/784.

The lower the necessary win rate, the higher the potential loss to potential win ratio becomes.

If you could win $50 "guaranteed" in 500 hands, then you could win $5000 by betting 100 times as much. It wouldn't take that long for this "secret" to get out, and then every casino in the world would go broke.

Repeat after me:
There is no such thing as a sure thing. That's why it's called "gambling."
(Well, unless you count the main event of the first WrestleMania, but (a) you have to go back in time to 1985, and (b) you have to find anyone who was taking bets on professional wrestling at the time.)
link to original post

I'm prepared to give him a system and a cast iron guarantee. He's to send me $1,000 for the system and if he can't use it to double his bankroll, I'll return his $1,000. Of course, what he loses in the process would be his problem.
$:o) $:o) $:o) $:o)


Sacke86, what you need to realise is that NO money management or betting system will help you gain an advantage over a negative expectation game. They can just change the timing of your ebb and flow of adrenaline.
See OnceDear's Rule of Thumb

Once 35% comes up, you know La Bouchere lurks in the background!

Quote: DeMango

Once 35% comes up, you know La Bouchere lurks in the background!
link to original post

For sure! I've grown a bankroll from $125 to $1325 at blackjack then I've withdrawn $600, up at $950 from $625 after that and I ended up with over $100 bets with a starting bet of just $4, catching a series of just 6 wins in 30 hands, wich is even worse, just 20% winrate in 30 hands but I don't think it's SF no more because it was just 30 hands after all and overall on all hands played I had over 45% winrate, I think.

Quote: OnceDear

Sacke86, what you need to realise is that NO money management or betting system will help you gain an advantage over a negative expectation game. They can just change the timing of your ebb and flow of adrenaline.
See OnceDear's Rule of Thumb
link to original post

I know negative EV can get you broke over a very long time but I'm just hoping that I'm lucky to make just a 10x and quit, wich I did at blackjack but I was greedy and I've withdrawn only 50%.

Quote: Sacke86

I know negative EV can get you broke over a very long time but I'm just hoping that I'm lucky to make just a 10x and quit, wich I did at blackjack but I was greedy and I've withdrawn only 50%.
link to original post

I have seldom known people to get off at the top of the rollercoaster. Don't bet the rent.

Best of luck in your endeavours.