When playing basic strategy, what are the odds of a player busting with a total of 22? 23? 24? etc...
Yeah, I'm playing around with a new BJ idea. For now, I'm just trying to get some ideas to see if the concept has any merit before I deep dive into the math.
This sort of thing is NOT what I'm looking for.Quote: MickyRatHit on 21 = 100% chance of busting
Hit on 20 = 92% chance of busting
Hit on 19 = 85% chance of busting
Hit on 18 = 77% chance of busting
Hit on 17 = 69% chance of busting
Hit on 16 = 62% chance of busting
Hit on 15 = 58% chance of busting
Hit on 14 = 56% chance of busting
Hit on 13 = 39% chance of busting
Hit on 12 = 31% chance of busting
link to original post
For one thing, it doesn't give any indication of playing strategy to arrive at those decision points. For another thing, it's not accurate.
Take the last line. Yeah, there'a a 31% chance of getting a 10 when hitting the 12. But it doesn't take into account getting a small card and having to hit again.
Having to hit again? With what objective?Quote: DJTeddyBearFor what it's worth, I found this from part of a 2014 post on WoV:
This sort of thing is NOT what I'm looking for.Quote: MickyRatHit on 21 = 100% chance of busting
Hit on 20 = 92% chance of busting
Hit on 19 = 85% chance of busting
Hit on 18 = 77% chance of busting
Hit on 17 = 69% chance of busting
Hit on 16 = 62% chance of busting
Hit on 15 = 58% chance of busting
Hit on 14 = 56% chance of busting
Hit on 13 = 39% chance of busting
Hit on 12 = 31% chance of busting
link to original post
For one thing, it doesn't give any indication of playing strategy to arrive at those decision points. For another thing, it's not accurate.
Take the last line. Yeah, there'a a 31% chance of getting a 10 when hitting the 12. But it doesn't take into account getting a small card and having to hit again.
link to original post
The table gives the odds of busting from that starting point. but I can't see what value there is in knowing the eventual probability of hitting say a hard 13 multiple times? When would you stop? take 7 aces and stand on twenty? Or need to know the probability of successfully going for the 21?
do you want the table expanded rightwards to
...
...
Hit on 12 = 31% of busting on 1 card XX% of busting on 2 cards YY% of busting on 3 cards.... etc?
I've seen people double down on a BJ and I once heard of a woman threaten a man who was back betting her much smaller bet to hit it unless he paid her a substantial fee. I'd have loved to have been there for that.
Quote: OnceDearHaving to hit again? With what objective?Quote: DJTeddyBearTake the last line. Yeah, there'a a 31% chance of getting a 10 when hitting the 12. But it doesn't take into account getting a small card and having to hit again.
I am assuming what the original poster is asking is this:
Playing basic strategy, in what fraction of hands does the player end up with 22, 23, 24, 25, and 26? (27 is not possible as you would have to hit a hard 17.)
If you hit 16 and get an Ace is that a 27?
Ah! I see The player IS playing basic strategy, so there will be distinct stopping points.Quote: ThatDonGuyQuote: OnceDearHaving to hit again? With what objective?Quote: DJTeddyBearTake the last line. Yeah, there'a a 31% chance of getting a 10 when hitting the 12. But it doesn't take into account getting a small card and having to hit again.
I am assuming what the original poster is asking is this:
Playing basic strategy, in what fraction of hands does the player end up with 22, 23, 24, 25, and 26? (27 is not possible as you would have to hit a hard 17.)
link to original post
BUT. that table would depend on, and vary with, the dealer's up card
Quote: DJTeddyBearI found a lot of useful info on the various WoO BJ pages, but nothing for the specific info I'm interested in.
When playing basic strategy, what are the odds of a player busting with a total of 22? 23? 24? etc...
Yeah, I'm playing around with a new BJ idea. For now, I'm just trying to get some ideas to see if the concept has any merit before I deep dive into the math.
link to original post
DJTeddyBear,
I ran a billion-round CVData sim for a heads-up B.S. player on a 6D, H17, DAS, 75% penetration game (you didn't specify conditions, so I picked 'em) and found the following percentages:
| 22 total | 4.524% |
| 23 total | 3.612% |
| 24 total | 3.127% |
| 25 total | 2.674% |
| 26 total | 2.084% |
| No Bust | 86.767% |
| Sum | 102.787% |
The percentages sum to over 100% due to splits.
Although you didn't specifically ask, below is a plot of the percentage for a B.S. player to end with each total versus the HiLo TC for -10 ≤ TC ≤ +10 (which contains over 99.9% or the rounds). The "# Bust" lines use the left-hand axis, while the "No Bust" green line uses the right-hand axis.
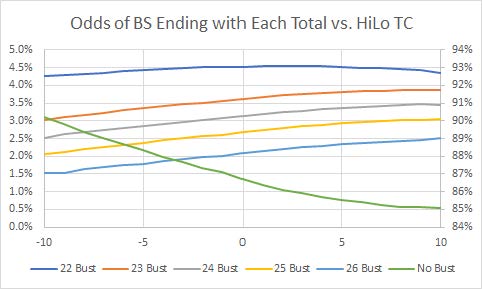
Note that the sim did not include surrender, which would naturally decrease the odds of busting.
Hope this helps!
Dog Hand
Quote: DogHand
DJTeddyBear,
I ran a billion-round CVData sim for a heads-up B.S. player on a 6D, H17, DAS, 75% penetration game (you didn't specify conditions, so I picked 'em) and found the following percentages:Quote: DJTeddyBearI found a lot of useful info on the various WoO BJ pages, but nothing for the specific info I'm interested in.
link to original post
Great work! Can you also plot the two charts for a dealer to bust at a total of 22, 23, 24, 25, and 26?
Quote: billryanI'm imagining a game where a player can win a side bet if he busts with exactly 22. How would the house handle someone who wanted to say they busted with two Aces?
link to original post
"Sir, you cannot bust with a total of hard two."
THANKS! 😁Quote: DogHandQuote: DJTeddyBearI found a lot of useful info on the various WoO BJ pages, but nothing for the specific info I'm interested in.
When playing basic strategy, what are the odds of a player busting with a total of 22? 23? 24? etc...
Yeah, I'm playing around with a new BJ idea. For now, I'm just trying to get some ideas to see if the concept has any merit before I deep dive into the math.
link to original post
DJTeddyBear,
I ran a billion-round CVData sim for a heads-up B.S. player on a 6D, H17, DAS, 75% penetration game (you didn't specify conditions, so I picked 'em) and found the following percentages:
22 total 4.524% 23 total 3.612% 24 total 3.127% 25 total 2.674% 26 total 2.084% No Bust 86.767% Sum 102.787%
The percentages sum to over 100% due to splits.
link to original post
Yeah. That’s the kind of data I was looking for. 👍
I might have to PM you for additional info.
And, yeah, I wish I had a simulator to do this myself. 🤪
Quote: DieterQuote: billryanI'm imagining a game where a player can win a side bet if he busts with exactly 22. How would the house handle someone who wanted to say they busted with two Aces?
link to original post
"Sir, you cannot bust with a total of hard two."
link to original post
I spent about two minutes researching and all three sites say a player's Ace can be a one or an eleven. It says the dealer's first Ace is an eleven unless it would bust the hand and all subsequent Aces count as one. Since most normal BJ games allow you to double down on a BJ,, it would seem the player gets to choose his Aces value. Would a pitboss refuse to allow it?
It's either watch the Pro Bowl or engage in fantasy blackjack.
Quote: billryanQuote: DieterQuote: billryanI'm imagining a game where a player can win a side bet if he busts with exactly 22. How would the house handle someone who wanted to say they busted with two Aces?
link to original post
"Sir, you cannot bust with a total of hard two."
link to original post
I spent about two minutes researching and all three sites say a player's Ace can be a one or an eleven. It says the dealer's first Ace is an eleven unless it would bust the hand and all subsequent Aces count as one. Since most normal BJ games allow you to double down on a BJ,, it would seem the player gets to choose his Aces value. Would a pitboss refuse to allow it?
It's either watch the Pro Bowl or engage in fantasy blackjack.
link to original post
I expect that the rules listed on the rack card will state that for the purposes of this wager, all aces shall be counted as 1 when determining the hand value.
Recently, I stumbled upon a YouTube video that the Wiz published where he shows how to create basic strategy in Excel with a companion video where he explains how to take that strategy document and come up with the house edge. And he included a link to the Excel document, which has both parts. Thanks Mike!
It's kinda complex, but also fascinating. The method used to keep taking hits as necessary is something I never would have thought of. And then calculating the value of hitting vs standing etc is really impressive. Nice work Mike!
But I do have one question about it, and I'd rather ask the gang here than ask Mike directly.
In the section where he talks about splits, the formula he enters is two times the value of hitting each individual card. For example, the value of spliting a pair of sixes is actually double value of taking a hit on a hard 6 would be. Double because each six becomes it's own hand.
It makes sense, except, it seems to me that this doesn't account for re-splits. Shouldn't the value be slightly more than double to account for re-splits?
If I'm wrong, I'd like someone to tell me why. If I'm right, I'd like to know how to calculate the correct multiplication factor.
Thanks.
AIUI, those spreadsheets don't account for resplits.Quote: DJTeddyBearAs I mentioned in the first post, I've been playing around with a potential new Blackjack variant.
Recently, I stumbled upon a YouTube video that the Wiz published where he shows how to create basic strategy in Excel with a companion video where he explains how to take that strategy document and come up with the house edge. And he included a link to the Excel document, which has both parts. Thanks Mike!
It's kinda complex, but also fascinating. The method used to keep taking hits as necessary is something I never would have thought of. And then calculating the value of hitting vs standing etc is really impressive. Nice work Mike!
But I do have one question about it, and I'd rather ask the gang here than ask Mike directly.
In the section where he talks about splits, the formula he enters is two times the value of hitting each individual card. For example, the value of spliting a pair of sixes is actually double value of taking a hit on a hard 6 would be. Double because each six becomes it's own hand.
It makes sense, except, it seems to me that this doesn't account for re-splits. Shouldn't the value be slightly more than double to account for re-splits?
If I'm wrong, I'd like someone to tell me why. If I'm right, I'd like to know how to calculate the correct multiplication factor.
Thanks.
link to original post
Quote: DJTeddyBearAs I mentioned in the first post, I've been playing around with a potential new Blackjack variant.
Recently, I stumbled upon a YouTube video that the Wiz published where he shows how to create basic strategy in Excel with a companion video where he explains how to take that strategy document and come up with the house edge. And he included a link to the Excel document, which has both parts. Thanks Mike!
It's kinda complex, but also fascinating. The method used to keep taking hits as necessary is something I never would have thought of. And then calculating the value of hitting vs standing etc is really impressive. Nice work Mike!
But I do have one question about it, and I'd rather ask the gang here than ask Mike directly.
In the section where he talks about splits, the formula he enters is two times the value of hitting each individual card. For example, the value of spliting a pair of sixes is actually double value of taking a hit on a hard 6 would be. Double because each six becomes it's own hand.
It makes sense, except, it seems to me that this doesn't account for re-splits. Shouldn't the value be slightly more than double to account for re-splits?
If I'm wrong, I'd like someone to tell me why. If I'm right, I'd like to know how to calculate the correct multiplication factor.
Thanks.
link to original post
Although the Wizard doesn't take resplitting into account in this YouTube video, there is a useful formula for doing so.
Let E0 be the expected value of the hand if no splitting were allowed. And let E1 be the expected value for the hand if only one split were allowed. (E1 is the number the Wizard calculates for each pair in the video.)
The formula for the EV of the hand where the player will re-split to a maximum of 3 times whenever possible, E3, is:
E3 = E0 + K * (E1 - E0)
where K = 1 + 2p + 4p2 - 6p3 + 2p4 where p = the probability of drawing a card of the same rank as the pair. (p =1/13 for non-tens, and p = 4/13 for ten-value cards)
The EV of the pair is the maximum of E0 and E3.
For example, suppose we wanted to calculate the infinite-deck EV of a pair of 6s vs 2 with 3 splits allowed. E0 would be the EV of hitting 12 vs 2; and E1 would be the EV of splitting 6s once vs 2, which equals twice the EV of 6 vs 2.
By the way, although we would never split a pair of 5s, E0 would be the EV of doubling 10 if doubling 10 were the correct play.
The above formula is for re-splitting non-aces, but a very similar formula can be applied to aces if ace re-splitting is allowed.
Quote: ChesterDogQuote: DJTeddyBearAs I mentioned in the first post, I've been playing around with a potential new Blackjack variant.
Recently, I stumbled upon a YouTube video that the Wiz published where he shows how to create basic strategy in Excel with a companion video where he explains how to take that strategy document and come up with the house edge. And he included a link to the Excel document, which has both parts. Thanks Mike!
It's kinda complex, but also fascinating. The method used to keep taking hits as necessary is something I never would have thought of. And then calculating the value of hitting vs standing etc is really impressive. Nice work Mike!
But I do have one question about it, and I'd rather ask the gang here than ask Mike directly.
In the section where he talks about splits, the formula he enters is two times the value of hitting each individual card. For example, the value of spliting a pair of sixes is actually double value of taking a hit on a hard 6 would be. Double because each six becomes it's own hand.
It makes sense, except, it seems to me that this doesn't account for re-splits. Shouldn't the value be slightly more than double to account for re-splits?
If I'm wrong, I'd like someone to tell me why. If I'm right, I'd like to know how to calculate the correct multiplication factor.
Thanks.
link to original post
Although the Wizard doesn't take resplitting into account in this YouTube video, there is a useful formula for doing so.
Let E0 be the expected value of the hand if no splitting were allowed. And let E1 be the expected value for the hand if only one split were allowed. (E1 is the number the Wizard calculates for each pair in the video.)
The formula for the EV of the hand where the player will re-split to a maximum of 3 times whenever possible, E3, is:
E3 = E0 + K * (E1 - E0)
where K = 1 + 2p + 4p2 - 6p3 + 2p4 where p = the probability of drawing a card of the same rank as the pair. (p =1/13 for non-tens, and p = 4/13 for ten-value cards)
The EV of the pair is the maximum of E0 and E3.
For example, suppose we wanted to calculate the infinite-deck EV of a pair of 6s vs 2 with 3 splits allowed. E0 would be the EV of hitting 12 vs 2; and E1 would be the EV of splitting 6s once vs 2, which equals twice the EV of 6 vs 2.
By the way, although we would never split a pair of 5s, E0 would be the EV of doubling 10 if doubling 10 were the correct play.
The above formula is for re-splitting non-aces, but a very similar formula can be applied to aces if ace re-splitting is allowed.
link to original post
What is the formula for the EV of the hand where the player will re-split to a maximum of 2 times whenever possible?
With both, every situations will be covered.
Quote: acesideQuote: ChesterDogQuote: DJTeddyBearAs I mentioned in the first post, I've been playing around with a potential new Blackjack variant.
Recently, I stumbled upon a YouTube video that the Wiz published where he shows how to create basic strategy in Excel with a companion video where he explains how to take that strategy document and come up with the house edge. And he included a link to the Excel document, which has both parts. Thanks Mike!
It's kinda complex, but also fascinating. The method used to keep taking hits as necessary is something I never would have thought of. And then calculating the value of hitting vs standing etc is really impressive. Nice work Mike!
But I do have one question about it, and I'd rather ask the gang here than ask Mike directly.
In the section where he talks about splits, the formula he enters is two times the value of hitting each individual card. For example, the value of spliting a pair of sixes is actually double value of taking a hit on a hard 6 would be. Double because each six becomes it's own hand.
It makes sense, except, it seems to me that this doesn't account for re-splits. Shouldn't the value be slightly more than double to account for re-splits?
If I'm wrong, I'd like someone to tell me why. If I'm right, I'd like to know how to calculate the correct multiplication factor.
Thanks.
link to original post
Although the Wizard doesn't take resplitting into account in this YouTube video, there is a useful formula for doing so.
Let E0 be the expected value of the hand if no splitting were allowed. And let E1 be the expected value for the hand if only one split were allowed. (E1 is the number the Wizard calculates for each pair in the video.)
The formula for the EV of the hand where the player will re-split to a maximum of 3 times whenever possible, E3, is:
E3 = E0 + K * (E1 - E0)
where K = 1 + 2p + 4p2 - 6p3 + 2p4 where p = the probability of drawing a card of the same rank as the pair. (p =1/13 for non-tens, and p = 4/13 for ten-value cards)
The EV of the pair is the maximum of E0 and E3.
For example, suppose we wanted to calculate the infinite-deck EV of a pair of 6s vs 2 with 3 splits allowed. E0 would be the EV of hitting 12 vs 2; and E1 would be the EV of splitting 6s once vs 2, which equals twice the EV of 6 vs 2.
By the way, although we would never split a pair of 5s, E0 would be the EV of doubling 10 if doubling 10 were the correct play.
The above formula is for re-splitting non-aces, but a very similar formula can be applied to aces if ace re-splitting is allowed.
link to original post
What is the formula for the EV of the hand where the player will re-split to a maximum of 2 times whenever possible?
With both, every situations will be covered.
link to original post
The formula for the EV of a non-aces pair split to a maximum of 2 times whenever possible is:
E2 = E0 + K*(E1 - E0),
where K = 1 + 2p - p2
But I've hurt my brain trying to wrap my head around your formula, specifically, to make it into an Excel calculation.
For example, the calucation the Wiz uses is = 2 * [whatever].
I substituted = ( 2 + 2/13 + (3/13)*(2/13) ) * [whatever]. This is:
2 for the original split, plus...
2/13 since there's 2 chances of matching the card, plus...
3/13 since there's 3 chances of a match of the three splits times 2/13 which is the odds that there was the original split.
Similarly, the paired tens line uses = 2 + 8/13 + (12/13)*(8/13) * [whatever].
Interestingly, this DOES change the strategy. Paired 3s vs 2 doesn't split, while paired 9s vs 7 and 10s ve 3 thru 7 all split.
It also changes the edge from 0.484% to a player advantage of 0.132%. That can't be right.
Can anybody help me figure out what I'm missing?
Thanks.
Quote: DJTeddyBearThanks ChesterDog.
But I've hurt my brain trying to wrap my head around your formula, specifically, to make it into an Excel calculation.
For example, the calucation the Wiz uses is = 2 * [whatever].
I substituted = ( 2 + 2/13 + (3/13)*(2/13) ) * [whatever]. This is:
2 for the original split, plus...
2/13 since there's 2 chances of matching the card, plus...
3/13 since there's 3 chances of a match of the three splits times 2/13 which is the odds that there was the original split.
Similarly, the paired tens line uses = 2 + 8/13 + (12/13)*(8/13) * [whatever].
Interestingly, this DOES change the strategy. Paired 3s vs 2 doesn't split, while paired 9s vs 7 and 10s ve 3 thru 7 all split.
It also changes the edge from 0.484% to a player advantage of 0.132%. That can't be right.
Can anybody help me figure out what I'm missing?
Thanks.
link to original post
Let me check if your coefficients are correct or not.
E_2 -E_0= (1+2/13 -(1/13)(1/13)) (E_1 -E_0).
Do we pick a maximum among E_0 and E_1 first? My logic is not very clear here.
The EV of the 2-max-split pair is the maximum of E_0 and E_2.
I don’t know how. Just a suggestion. Let ChesterDog come back.
Perhaps I can help you to apply ChesterDog's equation correctly.
Let's consider the case of 9,9 vs. 7. From the Wiz's spreadsheet, if you don't split, then the non-splitting highest EV option is to Stand (see cell G23 on the "split" worksheet), with an EV of 0.39955: this is what ChesterDog calls the E0 value.
The EV for a single split, what ChesterDog calls the E1 value is given in cell G9 as 0.37. Since E1 < E0, the Wiz's spreadsheet tells us not to split.
Now let's apply ChesterDog's equation!
Since we are contemplating a 9 split, p = 1/13: that is, the probability of drawing a 9 is 1 out of 13 for the infinite-deck case. That means the value of K is this:
K = 1 + 2p + 4p2 - 6p3 + 2p4 = 1 + 2/13 + 4/132 - 6/133 + 2/134 = 1.17485...
(Naturally, the K value is the same for splitting everything except 10's, since p = 1/13 for any rank other than 10.)*
Now, if we split 9's three times vs. the dealer's 7, then the EV is
E3 = E0 + K*(E1 - E0) = 0.39955 + 1.17485*(0.37 - 0.39955) = 0.36483
So, since E3 < E0, B.S. says NOT to split 9's vs. a 7.
By the way, if the Wiz's spreadsheet says NOT to split for his Sp1 case, then for Sp3 you also will not split.
Hope this helps!
Dog Hand
*Footnote: for a 10-split, p = 4/13 and so
K = 1 + 2p + 4p2 - 6p3 + 2p4 = 1 + 2*(4/13) + 4*(4/13)2 - 6*(4/13)3 + 2*(4/13)4 = 1.8372255...
Quote: DJTeddyBearThanks ChesterDog.
But I've hurt my brain trying to wrap my head around your formula, specifically, to make it into an Excel calculation.
For example, the calucation the Wiz uses is = 2 * [whatever].
I substituted = ( 2 + 2/13 + (3/13)*(2/13) ) * [whatever]. This is:
2 for the original split, plus...
2/13 since there's 2 chances of matching the card, plus...
3/13 since there's 3 chances of a match of the three splits times 2/13 which is the odds that there was the original split.
Similarly, the paired tens line uses = 2 + 8/13 + (12/13)*(8/13) * [whatever].
Interestingly, this DOES change the strategy. Paired 3s vs 2 doesn't split, while paired 9s vs 7 and 10s ve 3 thru 7 all split.
It also changes the edge from 0.484% to a player advantage of 0.132%. That can't be right.
Can anybody help me figure out what I'm missing?
Thanks.
link to original post
Rather than using the complicated formula for splitting up to three times, a more instructional approach to analyzing re-splitting is first to analyze infinite re-splitting.
As an example, let's use a pair of 3s vs dealer's 2. Let E1 stand for the EV of a pair of 3s allowing one split. We know the formula for E1 is:
E1 = (2/13) [E(soft 14) + E(5) + E(6) + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
where, for example, E(6) is the EV of hitting 6 vs 2 and E(10) is the EV of doubling 10 vs 2.
The formula for the EV of a pair of 3s vs dealer's 2 allowing infinite re-splitting, Einf., is just a little different. It's:
Einf. = (2/13) [E(soft 14) + E(5) + Einf. + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
Rearranging yields:
Einf. - (2/13)Einf.= (2/13) [E(soft 14) + E(5) + 0 + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
Then:
(11/13)Einf. = (2/13) [E(soft 14) + E(5) + 0 + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
Multiplying both sides by 13/11 yields:
Einf. = (2/11) [E(soft 14) + E(5) + 0 + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
A trick to make the Excel calculations easier is to replace the 0 with E(6) - E(6), where again E(6) is the EV of hitting 6 vs 2:
Einf. = (2/11) [E(soft 14) + E(5) + E(6) + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13) - E(6)]
We can simplify the above using the fact that E1 = (2/13) [E(soft 14) + E(5) + E(6) + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]. The final result is:
Einf. = (2/11) [(13/2)E1 - E(6)] = (13/11) E1 - (2/11)E(6)
And to determine if we should split 3s vs 2, we just compare Einf. with E(6).
The above formula can be used for pairs of 2s through 9s. (Of course, we would use E(4) for 2s, for example, instead of E(6).) The formula for 10s would be a little different because the probability of getting a 10 is 4/13. And since aces cannot usually be resplit, we would just use the one-split process.
E_3= E_0.
This cannot be done in iPhone?
(Typed on my phone. It's a hassle without a keyboard.)
And dieter beat me to the sub question. 🤪
Yeah, it’s a PITA on a phone, but doable.
Check the format codes link below the post button to learn how to do it.
Quote: DJTeddyBear
And dieter beat me to the sub question. 🤪
link to original post
I left some [sup]sup[/sup] for you if you're hungry?
Quote: ChesterDogQuote: DJTeddyBearThanks ChesterDog.
But I've hurt my brain trying to wrap my head around your formula, specifically, to make it into an Excel calculation.
For example, the calucation the Wiz uses is = 2 * [whatever].
I substituted = ( 2 + 2/13 + (3/13)*(2/13) ) * [whatever]. This is:
2 for the original split, plus...
2/13 since there's 2 chances of matching the card, plus...
3/13 since there's 3 chances of a match of the three splits times 2/13 which is the odds that there was the original split.
Similarly, the paired tens line uses = 2 + 8/13 + (12/13)*(8/13) * [whatever].
Interestingly, this DOES change the strategy. Paired 3s vs 2 doesn't split, while paired 9s vs 7 and 10s ve 3 thru 7 all split.
It also changes the edge from 0.484% to a player advantage of 0.132%. That can't be right.
Can anybody help me figure out what I'm missing?
Thanks.
link to original post
Rather than using the complicated formula for splitting up to three times, a more instructional approach to analyzing re-splitting is first to analyze infinite re-splitting.
As an example, let's use a pair of 3s vs dealer's 2. Let E1 stand for the EV of a pair of 3s allowing one split. We know the formula for E1 is:
E1 = (2/13) [E(soft 14) + E(5) + E(6) + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
where, for example, E(6) is the EV of hitting 6 vs 2 and E(10) is the EV of doubling 10 vs 2.
The formula for the EV of a pair of 3s vs dealer's 2 allowing infinite re-splitting, Einf., is just a little different. It's:
Einf. = (2/13) [E(soft 14) + E(5) + Einf. + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
Rearranging yields:
Einf. - (2/13)Einf.= (2/13) [E(soft 14) + E(5) + 0 + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
Then:
(11/13)Einf. = (2/13) [E(soft 14) + E(5) + 0 + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
Multiplying both sides by 13/11 yields:
Einf. = (2/11) [E(soft 14) + E(5) + 0 + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
A trick to make the Excel calculations easier is to replace the 0 with E(6) - E(6), where again E(6) is the EV of hitting 6 vs 2:
Einf. = (2/11) [E(soft 14) + E(5) + E(6) + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13) - E(6)]
We can simplify the above using the fact that E1 = (2/13) [E(soft 14) + E(5) + E(6) + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]. The final result is:
Einf. = (2/11) [(13/2)E1 - E(6)] = (13/11) E1 - (2/11)E(6)
And to determine if we should split 3s vs 2, we just compare Einf. with E(6).
The above formula can be used for pairs of 2s through 9s. (Of course, we would use E(4) for 2s, for example, instead of E(6).) The formula for 10s would be a little different because the probability of getting a 10 is 4/13. And since aces cannot usually be resplit, we would just use the one-split process.
link to original post
I have followed yours and Dog Hand's instructions to get the expected results. They all seem good to me. However, to explore this a little more, I have two new questions and greatly hope you can help:
The formula for the EV of a non-aces pair split to a maximum of 2 times:
E_2 = E_0 + K*(E_1 - E_0), where K = 1 + 2p - p^2
The formula for the EV of a non-aces pair split to a maximum of 3 times:
E_3 = E_0 + K*(E_1 - E_0), where K = 1 + 2p + 4p^2 - 6p^3 + 2p^4
The formula for the EV of a non-aces pair split to a maximum of n times:
E_n = E_0 + K*(E_1 - E_0), where K= what?
The formula for the EV of a non-aces pair split to a maximum of infinite times:
E_inf = E_0 + K*(E_1 - E_0), where K = what?
Quote: acesideQuote: ChesterDogQuote: DJTeddyBearThanks ChesterDog.
But I've hurt my brain trying to wrap my head around your formula, specifically, to make it into an Excel calculation.
For example, the calucation the Wiz uses is = 2 * [whatever].
I substituted = ( 2 + 2/13 + (3/13)*(2/13) ) * [whatever]. This is:
2 for the original split, plus...
2/13 since there's 2 chances of matching the card, plus...
3/13 since there's 3 chances of a match of the three splits times 2/13 which is the odds that there was the original split.
Similarly, the paired tens line uses = 2 + 8/13 + (12/13)*(8/13) * [whatever].
Interestingly, this DOES change the strategy. Paired 3s vs 2 doesn't split, while paired 9s vs 7 and 10s ve 3 thru 7 all split.
It also changes the edge from 0.484% to a player advantage of 0.132%. That can't be right.
Can anybody help me figure out what I'm missing?
Thanks.
link to original post
Rather than using the complicated formula for splitting up to three times, a more instructional approach to analyzing re-splitting is first to analyze infinite re-splitting.
As an example, let's use a pair of 3s vs dealer's 2. Let E1 stand for the EV of a pair of 3s allowing one split. We know the formula for E1 is:
E1 = (2/13) [E(soft 14) + E(5) + E(6) + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
where, for example, E(6) is the EV of hitting 6 vs 2 and E(10) is the EV of doubling 10 vs 2.
The formula for the EV of a pair of 3s vs dealer's 2 allowing infinite re-splitting, Einf., is just a little different. It's:
Einf. = (2/13) [E(soft 14) + E(5) + Einf. + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
Rearranging yields:
Einf. - (2/13)Einf.= (2/13) [E(soft 14) + E(5) + 0 + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
Then:
(11/13)Einf. = (2/13) [E(soft 14) + E(5) + 0 + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
Multiplying both sides by 13/11 yields:
Einf. = (2/11) [E(soft 14) + E(5) + 0 + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
A trick to make the Excel calculations easier is to replace the 0 with E(6) - E(6), where again E(6) is the EV of hitting 6 vs 2:
Einf. = (2/11) [E(soft 14) + E(5) + E(6) + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13) - E(6)]
We can simplify the above using the fact that E1 = (2/13) [E(soft 14) + E(5) + E(6) + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]. The final result is:
Einf. = (2/11) [(13/2)E1 - E(6)] = (13/11) E1 - (2/11)E(6)
And to determine if we should split 3s vs 2, we just compare Einf. with E(6).
The above formula can be used for pairs of 2s through 9s. (Of course, we would use E(4) for 2s, for example, instead of E(6).) The formula for 10s would be a little different because the probability of getting a 10 is 4/13. And since aces cannot usually be resplit, we would just use the one-split process.
link to original post
I have followed yours and Dog Hand's instructions to get the expected results. They all seem good to me. However, to explore this a little more, I have two new questions and greatly hope you can help:
The formula for the EV of a non-aces pair split to a maximum of 2 times:
E_2 = E_0 + K*(E_1 - E_0), where K = 1 + 2p - p^2
The formula for the EV of a non-aces pair split to a maximum of 3 times:
E_3 = E_0 + K*(E_1 - E_0), where K = 1 + 2p + 4p^2 - 6p^3 + 2p^4
The formula for the EV of a non-aces pair split to a maximum of n times:
E_n = E_0 + K*(E_1 - E_0), where K= what?
The formula for the EV of a non-aces pair split to a maximum of infinite times:
E_inf = E_0 + K*(E_1 - E_0), where K = what?
link to original post
I figured out the last part myself.
The formula for the EV of a non-aces pair split to a maximum of infinite times:
E_inf = E_0 + K*(E_1 - E_0), where K = 1/(1-2p)
Quote: acesideQuote: acesideQuote: ChesterDogQuote: DJTeddyBearThanks ChesterDog.
But I've hurt my brain trying to wrap my head around your formula, specifically, to make it into an Excel calculation.
For example, the calucation the Wiz uses is = 2 * [whatever].
I substituted = ( 2 + 2/13 + (3/13)*(2/13) ) * [whatever]. This is:
2 for the original split, plus...
2/13 since there's 2 chances of matching the card, plus...
3/13 since there's 3 chances of a match of the three splits times 2/13 which is the odds that there was the original split.
Similarly, the paired tens line uses = 2 + 8/13 + (12/13)*(8/13) * [whatever].
Interestingly, this DOES change the strategy. Paired 3s vs 2 doesn't split, while paired 9s vs 7 and 10s ve 3 thru 7 all split.
It also changes the edge from 0.484% to a player advantage of 0.132%. That can't be right.
Can anybody help me figure out what I'm missing?
Thanks.
link to original post
Rather than using the complicated formula for splitting up to three times, a more instructional approach to analyzing re-splitting is first to analyze infinite re-splitting.
As an example, let's use a pair of 3s vs dealer's 2. Let E1 stand for the EV of a pair of 3s allowing one split. We know the formula for E1 is:
E1 = (2/13) [E(soft 14) + E(5) + E(6) + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
where, for example, E(6) is the EV of hitting 6 vs 2 and E(10) is the EV of doubling 10 vs 2.
The formula for the EV of a pair of 3s vs dealer's 2 allowing infinite re-splitting, Einf., is just a little different. It's:
Einf. = (2/13) [E(soft 14) + E(5) + Einf. + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
Rearranging yields:
Einf. - (2/13)Einf.= (2/13) [E(soft 14) + E(5) + 0 + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
Then:
(11/13)Einf. = (2/13) [E(soft 14) + E(5) + 0 + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
Multiplying both sides by 13/11 yields:
Einf. = (2/11) [E(soft 14) + E(5) + 0 + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
A trick to make the Excel calculations easier is to replace the 0 with E(6) - E(6), where again E(6) is the EV of hitting 6 vs 2:
Einf. = (2/11) [E(soft 14) + E(5) + E(6) + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13) - E(6)]
We can simplify the above using the fact that E1 = (2/13) [E(soft 14) + E(5) + E(6) + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]. The final result is:
Einf. = (2/11) [(13/2)E1 - E(6)] = (13/11) E1 - (2/11)E(6)
And to determine if we should split 3s vs 2, we just compare Einf. with E(6).
The above formula can be used for pairs of 2s through 9s. (Of course, we would use E(4) for 2s, for example, instead of E(6).) The formula for 10s would be a little different because the probability of getting a 10 is 4/13. And since aces cannot usually be resplit, we would just use the one-split process.
link to original post
I have followed yours and Dog Hand's instructions to get the expected results. They all seem good to me. However, to explore this a little more, I have two new questions and greatly hope you can help:
The formula for the EV of a non-aces pair split to a maximum of 2 times:
E_2 = E_0 + K*(E_1 - E_0), where K = 1 + 2p - p^2
The formula for the EV of a non-aces pair split to a maximum of 3 times:
E_3 = E_0 + K*(E_1 - E_0), where K = 1 + 2p + 4p^2 - 6p^3 + 2p^4
The formula for the EV of a non-aces pair split to a maximum of n times:
E_n = E_0 + K*(E_1 - E_0), where K= what?
The formula for the EV of a non-aces pair split to a maximum of infinite times:
E_inf = E_0 + K*(E_1 - E_0), where K = what?
link to original post
I figured out the last part myself.
The formula for the EV of a non-aces pair split to a maximum of infinite times:
E_inf = E_0 + K*(E_1 - E_0), where K = 1/(1-2p)
link to original post
Yes, I agree that K =1/(1-2p) for the infinite re-splitting formula.
By the way, I find it interesting that 1/(1-2p) = 1 + 2p + 4p2 + 8p3 + 16p4 + . . . and that the first three terms of this infinite series match those of the formula for the three-splits formula, K = 1 + 2p + 4p2 - 6p3 + 2p4
Quote: ChesterDogQuote: acesideQuote: acesideQuote: ChesterDogQuote: DJTeddyBearThanks ChesterDog.
But I've hurt my brain trying to wrap my head around your formula, specifically, to make it into an Excel calculation.
For example, the calucation the Wiz uses is = 2 * [whatever].
I substituted = ( 2 + 2/13 + (3/13)*(2/13) ) * [whatever]. This is:
2 for the original split, plus...
2/13 since there's 2 chances of matching the card, plus...
3/13 since there's 3 chances of a match of the three splits times 2/13 which is the odds that there was the original split.
Similarly, the paired tens line uses = 2 + 8/13 + (12/13)*(8/13) * [whatever].
Interestingly, this DOES change the strategy. Paired 3s vs 2 doesn't split, while paired 9s vs 7 and 10s ve 3 thru 7 all split.
It also changes the edge from 0.484% to a player advantage of 0.132%. That can't be right.
Can anybody help me figure out what I'm missing?
Thanks.
link to original post
Rather than using the complicated formula for splitting up to three times, a more instructional approach to analyzing re-splitting is first to analyze infinite re-splitting.
As an example, let's use a pair of 3s vs dealer's 2. Let E1 stand for the EV of a pair of 3s allowing one split. We know the formula for E1 is:
E1 = (2/13) [E(soft 14) + E(5) + E(6) + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
where, for example, E(6) is the EV of hitting 6 vs 2 and E(10) is the EV of doubling 10 vs 2.
The formula for the EV of a pair of 3s vs dealer's 2 allowing infinite re-splitting, Einf., is just a little different. It's:
Einf. = (2/13) [E(soft 14) + E(5) + Einf. + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
Rearranging yields:
Einf. - (2/13)Einf.= (2/13) [E(soft 14) + E(5) + 0 + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
Then:
(11/13)Einf. = (2/13) [E(soft 14) + E(5) + 0 + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
Multiplying both sides by 13/11 yields:
Einf. = (2/11) [E(soft 14) + E(5) + 0 + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
A trick to make the Excel calculations easier is to replace the 0 with E(6) - E(6), where again E(6) is the EV of hitting 6 vs 2:
Einf. = (2/11) [E(soft 14) + E(5) + E(6) + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13) - E(6)]
We can simplify the above using the fact that E1 = (2/13) [E(soft 14) + E(5) + E(6) + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]. The final result is:
Einf. = (2/11) [(13/2)E1 - E(6)] = (13/11) E1 - (2/11)E(6)
And to determine if we should split 3s vs 2, we just compare Einf. with E(6).
The above formula can be used for pairs of 2s through 9s. (Of course, we would use E(4) for 2s, for example, instead of E(6).) The formula for 10s would be a little different because the probability of getting a 10 is 4/13. And since aces cannot usually be resplit, we would just use the one-split process.
link to original post
I have followed yours and Dog Hand's instructions to get the expected results. They all seem good to me. However, to explore this a little more, I have two new questions and greatly hope you can help:
The formula for the EV of a non-aces pair split to a maximum of 2 times:
E_2 = E_0 + K*(E_1 - E_0), where K = 1 + 2p - p^2
The formula for the EV of a non-aces pair split to a maximum of 3 times:
E_3 = E_0 + K*(E_1 - E_0), where K = 1 + 2p + 4p^2 - 6p^3 + 2p^4
The formula for the EV of a non-aces pair split to a maximum of n times:
E_n = E_0 + K*(E_1 - E_0), where K= what?
The formula for the EV of a non-aces pair split to a maximum of infinite times:
E_inf = E_0 + K*(E_1 - E_0), where K = what?
link to original post
I figured out the last part myself.
The formula for the EV of a non-aces pair split to a maximum of infinite times:
E_inf = E_0 + K*(E_1 - E_0), where K = 1/(1-2p)
link to original post
Yes, I agree that K =1/(1-2p) for the infinite re-splitting formula.
By the way, I find it interesting that 1/(1-2p) = 1 + 2p + 4p2 + 8p3 + 16p4 + . . . and that the first three terms of this infinite series match those of the formula for the three-splits formula, K = 1 + 2p + 4p2 - 6p3 + 2p4
link to original post
The problem is my coefficients K’s do not match to yours. Any thoughts? Based on this math, the coefficients K’s should be:
The formula for the EV of a non-aces pair split to a maximum of 2 times:
E_2 = E_0 + K*(E_1 - E_0), where K = 1 + 2p
The formula for the EV of a non-aces pair split to a maximum of 3 times:
E_3 = E_0 + K*(E_1 - E_0), where K = 1 + 2p + 4p^2
The formula for the EV of a non-aces pair split to a maximum of n times:
E_n = E_0 + K*(E_1 - E_0), where K= 1 +2p +4p^2 +…+(2p)^n
The formula for the EV of a non-aces pair split to a maximum of infinite times:
E_inf = E_0 + K*(E_1 - E_0), where K = 1/(1-2p)
Quote: acesideQuote: ChesterDogQuote: acesideQuote: acesideQuote: ChesterDogQuote: DJTeddyBearThanks ChesterDog.
But I've hurt my brain trying to wrap my head around your formula, specifically, to make it into an Excel calculation.
For example, the calucation the Wiz uses is = 2 * [whatever].
I substituted = ( 2 + 2/13 + (3/13)*(2/13) ) * [whatever]. This is:
2 for the original split, plus...
2/13 since there's 2 chances of matching the card, plus...
3/13 since there's 3 chances of a match of the three splits times 2/13 which is the odds that there was the original split.
Similarly, the paired tens line uses = 2 + 8/13 + (12/13)*(8/13) * [whatever].
Interestingly, this DOES change the strategy. Paired 3s vs 2 doesn't split, while paired 9s vs 7 and 10s ve 3 thru 7 all split.
It also changes the edge from 0.484% to a player advantage of 0.132%. That can't be right.
Can anybody help me figure out what I'm missing?
Thanks.
link to original post
Rather than using the complicated formula for splitting up to three times, a more instructional approach to analyzing re-splitting is first to analyze infinite re-splitting.
As an example, let's use a pair of 3s vs dealer's 2. Let E1 stand for the EV of a pair of 3s allowing one split. We know the formula for E1 is:
E1 = (2/13) [E(soft 14) + E(5) + E(6) + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
where, for example, E(6) is the EV of hitting 6 vs 2 and E(10) is the EV of doubling 10 vs 2.
The formula for the EV of a pair of 3s vs dealer's 2 allowing infinite re-splitting, Einf., is just a little different. It's:
Einf. = (2/13) [E(soft 14) + E(5) + Einf. + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
Rearranging yields:
Einf. - (2/13)Einf.= (2/13) [E(soft 14) + E(5) + 0 + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
Then:
(11/13)Einf. = (2/13) [E(soft 14) + E(5) + 0 + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
Multiplying both sides by 13/11 yields:
Einf. = (2/11) [E(soft 14) + E(5) + 0 + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
A trick to make the Excel calculations easier is to replace the 0 with E(6) - E(6), where again E(6) is the EV of hitting 6 vs 2:
Einf. = (2/11) [E(soft 14) + E(5) + E(6) + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13) - E(6)]
We can simplify the above using the fact that E1 = (2/13) [E(soft 14) + E(5) + E(6) + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]. The final result is:
Einf. = (2/11) [(13/2)E1 - E(6)] = (13/11) E1 - (2/11)E(6)
And to determine if we should split 3s vs 2, we just compare Einf. with E(6).
The above formula can be used for pairs of 2s through 9s. (Of course, we would use E(4) for 2s, for example, instead of E(6).) The formula for 10s would be a little different because the probability of getting a 10 is 4/13. And since aces cannot usually be resplit, we would just use the one-split process.
link to original post
I have followed yours and Dog Hand's instructions to get the expected results. They all seem good to me. However, to explore this a little more, I have two new questions and greatly hope you can help:
The formula for the EV of a non-aces pair split to a maximum of 2 times:
E_2 = E_0 + K*(E_1 - E_0), where K = 1 + 2p - p^2
The formula for the EV of a non-aces pair split to a maximum of 3 times:
E_3 = E_0 + K*(E_1 - E_0), where K = 1 + 2p + 4p^2 - 6p^3 + 2p^4
The formula for the EV of a non-aces pair split to a maximum of n times:
E_n = E_0 + K*(E_1 - E_0), where K= what?
The formula for the EV of a non-aces pair split to a maximum of infinite times:
E_inf = E_0 + K*(E_1 - E_0), where K = what?
link to original post
I figured out the last part myself.
The formula for the EV of a non-aces pair split to a maximum of infinite times:
E_inf = E_0 + K*(E_1 - E_0), where K = 1/(1-2p)
link to original post
Yes, I agree that K =1/(1-2p) for the infinite re-splitting formula.
By the way, I find it interesting that 1/(1-2p) = 1 + 2p + 4p2 + 8p3 + 16p4 + . . . and that the first three terms of this infinite series match those of the formula for the three-splits formula, K = 1 + 2p + 4p2 - 6p3 + 2p4
link to original post
The problem is my coefficients K’s do not match to yours. Any thoughts? Based on this math, the coefficients K’s should be:
The formula for the EV of a non-aces pair split to a maximum of 2 times:
E_2 = E_0 + K*(E_1 - E_0), where K = 1 + 2p
The formula for the EV of a non-aces pair split to a maximum of 3 times:
E_3 = E_0 + K*(E_1 - E_0), where K = 1 + 2p + 4p^2
The formula for the EV of a non-aces pair split to a maximum of n times:
E_n = E_0 + K*(E_1 - E_0), where K= 1 +2p +4p^2 +…+(2p)^n
The formula for the EV of a non-aces pair split to a maximum of infinite times:
E_inf = E_0 + K*(E_1 - E_0), where K = 1/(1-2p)
link to original post
I was thinking about our differences in the values of K on and off all today. Finally, I thought of a simple thought experiment that would help settle the problem.
Suppose we have a new game. We have an infinite deck of cards consists of 75% aces and 25% tens. Any hand of one ace and one ten is worth 1, and all other hands are worth 0.
Let's find the values of the hand TT if we stand (E0), split to a maximum of once (E1), or split to a maximum of twice (E2). Let p = the probability of pulling a ten = 0.25
Then we can compare the directly calculated value of E2 with E0 + (1 + 2p)(E1 - E0) and E0 + (1 + 2p - p2)(E1 - E0) to see if either matches.
Quote: ChesterDogQuote: acesideQuote: ChesterDogQuote: acesideQuote: acesideQuote: ChesterDogQuote: DJTeddyBearThanks ChesterDog.
But I've hurt my brain trying to wrap my head around your formula, specifically, to make it into an Excel calculation.
For example, the calucation the Wiz uses is = 2 * [whatever].
I substituted = ( 2 + 2/13 + (3/13)*(2/13) ) * [whatever]. This is:
2 for the original split, plus...
2/13 since there's 2 chances of matching the card, plus...
3/13 since there's 3 chances of a match of the three splits times 2/13 which is the odds that there was the original split.
Similarly, the paired tens line uses = 2 + 8/13 + (12/13)*(8/13) * [whatever].
Interestingly, this DOES change the strategy. Paired 3s vs 2 doesn't split, while paired 9s vs 7 and 10s ve 3 thru 7 all split.
It also changes the edge from 0.484% to a player advantage of 0.132%. That can't be right.
Can anybody help me figure out what I'm missing?
Thanks.
link to original post
Rather than using the complicated formula for splitting up to three times, a more instructional approach to analyzing re-splitting is first to analyze infinite re-splitting.
As an example, let's use a pair of 3s vs dealer's 2. Let E1 stand for the EV of a pair of 3s allowing one split. We know the formula for E1 is:
E1 = (2/13) [E(soft 14) + E(5) + E(6) + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
where, for example, E(6) is the EV of hitting 6 vs 2 and E(10) is the EV of doubling 10 vs 2.
The formula for the EV of a pair of 3s vs dealer's 2 allowing infinite re-splitting, Einf., is just a little different. It's:
Einf. = (2/13) [E(soft 14) + E(5) + Einf. + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
Rearranging yields:
Einf. - (2/13)Einf.= (2/13) [E(soft 14) + E(5) + 0 + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
Then:
(11/13)Einf. = (2/13) [E(soft 14) + E(5) + 0 + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
Multiplying both sides by 13/11 yields:
Einf. = (2/11) [E(soft 14) + E(5) + 0 + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
A trick to make the Excel calculations easier is to replace the 0 with E(6) - E(6), where again E(6) is the EV of hitting 6 vs 2:
Einf. = (2/11) [E(soft 14) + E(5) + E(6) + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13) - E(6)]
We can simplify the above using the fact that E1 = (2/13) [E(soft 14) + E(5) + E(6) + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]. The final result is:
Einf. = (2/11) [(13/2)E1 - E(6)] = (13/11) E1 - (2/11)E(6)
And to determine if we should split 3s vs 2, we just compare Einf. with E(6).
The above formula can be used for pairs of 2s through 9s. (Of course, we would use E(4) for 2s, for example, instead of E(6).) The formula for 10s would be a little different because the probability of getting a 10 is 4/13. And since aces cannot usually be resplit, we would just use the one-split process.
link to original post
I have followed yours and Dog Hand's instructions to get the expected results. They all seem good to me. However, to explore this a little more, I have two new questions and greatly hope you can help:
The formula for the EV of a non-aces pair split to a maximum of 2 times:
E_2 = E_0 + K*(E_1 - E_0), where K = 1 + 2p - p^2
The formula for the EV of a non-aces pair split to a maximum of 3 times:
E_3 = E_0 + K*(E_1 - E_0), where K = 1 + 2p + 4p^2 - 6p^3 + 2p^4
The formula for the EV of a non-aces pair split to a maximum of n times:
E_n = E_0 + K*(E_1 - E_0), where K= what?
The formula for the EV of a non-aces pair split to a maximum of infinite times:
E_inf = E_0 + K*(E_1 - E_0), where K = what?
link to original post
I figured out the last part myself.
The formula for the EV of a non-aces pair split to a maximum of infinite times:
E_inf = E_0 + K*(E_1 - E_0), where K = 1/(1-2p)
link to original post
Yes, I agree that K =1/(1-2p) for the infinite re-splitting formula.
By the way, I find it interesting that 1/(1-2p) = 1 + 2p + 4p2 + 8p3 + 16p4 + . . . and that the first three terms of this infinite series match those of the formula for the three-splits formula, K = 1 + 2p + 4p2 - 6p3 + 2p4
link to original post
The problem is my coefficients K’s do not match to yours. Any thoughts? Based on this math, the coefficients K’s should be:
The formula for the EV of a non-aces pair split to a maximum of 2 times:
E_2 = E_0 + K*(E_1 - E_0), where K = 1 + 2p
The formula for the EV of a non-aces pair split to a maximum of 3 times:
E_3 = E_0 + K*(E_1 - E_0), where K = 1 + 2p + 4p^2
The formula for the EV of a non-aces pair split to a maximum of n times:
E_n = E_0 + K*(E_1 - E_0), where K= 1 +2p +4p^2 +…+(2p)^n
The formula for the EV of a non-aces pair split to a maximum of infinite times:
E_inf = E_0 + K*(E_1 - E_0), where K = 1/(1-2p)
link to original post
I was thinking about our differences in the values of K on and off all today. Finally, I thought of a simple thought experiment that would help settle the problem.
Suppose we have a new game. We have an infinite deck of cards consists of 75% aces and 25% tens. Any hand of one ace and one ten is worth 1, and all other hands are worth 0.
Let's find the values of the hand TT if we stand (E0), split to a maximum of once (E1), or split to a maximum of twice (E2). Let p = the probability of pulling a ten = 0.25
Then we can compare the directly calculated value of E2 with E0 + (1 + 2p)(E1 - E0) and E0 + (1 + 2p - p2)(E1 - E0) to see if either matches.
link to original post
This problem is tricky. To verify the coefficient K, I have tried your simplified mathematical model using the infinite deck of aces (75%) and (25%) tens. In the EV formula of a non-aces pair split to a maximum of 2 times,
E_2 = E_0 + K*(E_1 - E_0),
I got the coefficient K = 1 + 2p-2p^2. It is neither 1+2p, nor 1 + 2p-p^2.
This also makes me think that the coefficient K in the infinite-time split case may have some problem. You used a pair of 3s vs dealer's 2 to demonstrate the derivation (E_1 stand for the EV of a pair of 3s allowing one split, and E_0 stand for the EV of a pair of 3s without splitting) and showed
E1 = (2/13) [E(soft 14) + E(5) + E_0 + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)],
but the derivation from E_1 to E_2 is still not clear to me. This part is my headache.
How did you get the coefficient K = 1 + 2p + 4p^2 - 6p^3 + 2p^4 , when a 3-time-maximum split is allowed?
Quote: acesideQuote: ChesterDogQuote: acesideQuote: ChesterDogQuote: acesideQuote: acesideQuote: ChesterDogQuote: DJTeddyBearThanks ChesterDog.
But I've hurt my brain trying to wrap my head around your formula, specifically, to make it into an Excel calculation.
For example, the calucation the Wiz uses is = 2 * [whatever].
I substituted = ( 2 + 2/13 + (3/13)*(2/13) ) * [whatever]. This is:
2 for the original split, plus...
2/13 since there's 2 chances of matching the card, plus...
3/13 since there's 3 chances of a match of the three splits times 2/13 which is the odds that there was the original split.
Similarly, the paired tens line uses = 2 + 8/13 + (12/13)*(8/13) * [whatever].
Interestingly, this DOES change the strategy. Paired 3s vs 2 doesn't split, while paired 9s vs 7 and 10s ve 3 thru 7 all split.
It also changes the edge from 0.484% to a player advantage of 0.132%. That can't be right.
Can anybody help me figure out what I'm missing?
Thanks.
link to original post
Rather than using the complicated formula for splitting up to three times, a more instructional approach to analyzing re-splitting is first to analyze infinite re-splitting.
As an example, let's use a pair of 3s vs dealer's 2. Let E1 stand for the EV of a pair of 3s allowing one split. We know the formula for E1 is:
E1 = (2/13) [E(soft 14) + E(5) + E(6) + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
where, for example, E(6) is the EV of hitting 6 vs 2 and E(10) is the EV of doubling 10 vs 2.
The formula for the EV of a pair of 3s vs dealer's 2 allowing infinite re-splitting, Einf., is just a little different. It's:
Einf. = (2/13) [E(soft 14) + E(5) + Einf. + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
Rearranging yields:
Einf. - (2/13)Einf.= (2/13) [E(soft 14) + E(5) + 0 + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
Then:
(11/13)Einf. = (2/13) [E(soft 14) + E(5) + 0 + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
Multiplying both sides by 13/11 yields:
Einf. = (2/11) [E(soft 14) + E(5) + 0 + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
A trick to make the Excel calculations easier is to replace the 0 with E(6) - E(6), where again E(6) is the EV of hitting 6 vs 2:
Einf. = (2/11) [E(soft 14) + E(5) + E(6) + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13) - E(6)]
We can simplify the above using the fact that E1 = (2/13) [E(soft 14) + E(5) + E(6) + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]. The final result is:
Einf. = (2/11) [(13/2)E1 - E(6)] = (13/11) E1 - (2/11)E(6)
And to determine if we should split 3s vs 2, we just compare Einf. with E(6).
The above formula can be used for pairs of 2s through 9s. (Of course, we would use E(4) for 2s, for example, instead of E(6).) The formula for 10s would be a little different because the probability of getting a 10 is 4/13. And since aces cannot usually be resplit, we would just use the one-split process.
link to original post
I have followed yours and Dog Hand's instructions to get the expected results. They all seem good to me. However, to explore this a little more, I have two new questions and greatly hope you can help:
The formula for the EV of a non-aces pair split to a maximum of 2 times:
E_2 = E_0 + K*(E_1 - E_0), where K = 1 + 2p - p^2
The formula for the EV of a non-aces pair split to a maximum of 3 times:
E_3 = E_0 + K*(E_1 - E_0), where K = 1 + 2p + 4p^2 - 6p^3 + 2p^4
The formula for the EV of a non-aces pair split to a maximum of n times:
E_n = E_0 + K*(E_1 - E_0), where K= what?
The formula for the EV of a non-aces pair split to a maximum of infinite times:
E_inf = E_0 + K*(E_1 - E_0), where K = what?
link to original post
I figured out the last part myself.
The formula for the EV of a non-aces pair split to a maximum of infinite times:
E_inf = E_0 + K*(E_1 - E_0), where K = 1/(1-2p)
link to original post
Yes, I agree that K =1/(1-2p) for the infinite re-splitting formula.
By the way, I find it interesting that 1/(1-2p) = 1 + 2p + 4p2 + 8p3 + 16p4 + . . . and that the first three terms of this infinite series match those of the formula for the three-splits formula, K = 1 + 2p + 4p2 - 6p3 + 2p4
link to original post
The problem is my coefficients K’s do not match to yours. Any thoughts? Based on this math, the coefficients K’s should be:
The formula for the EV of a non-aces pair split to a maximum of 2 times:
E_2 = E_0 + K*(E_1 - E_0), where K = 1 + 2p
The formula for the EV of a non-aces pair split to a maximum of 3 times:
E_3 = E_0 + K*(E_1 - E_0), where K = 1 + 2p + 4p^2
The formula for the EV of a non-aces pair split to a maximum of n times:
E_n = E_0 + K*(E_1 - E_0), where K= 1 +2p +4p^2 +…+(2p)^n
The formula for the EV of a non-aces pair split to a maximum of infinite times:
E_inf = E_0 + K*(E_1 - E_0), where K = 1/(1-2p)
link to original post
I was thinking about our differences in the values of K on and off all today. Finally, I thought of a simple thought experiment that would help settle the problem.
Suppose we have a new game. We have an infinite deck of cards consists of 75% aces and 25% tens. Any hand of one ace and one ten is worth 1, and all other hands are worth 0.
Let's find the values of the hand TT if we stand (E0), split to a maximum of once (E1), or split to a maximum of twice (E2). Let p = the probability of pulling a ten = 0.25
Then we can compare the directly calculated value of E2 with E0 + (1 + 2p)(E1 - E0) and E0 + (1 + 2p - p2)(E1 - E0) to see if either matches.
link to original post
This problem is tricky. To verify the coefficient K, I have tried your simplified mathematical model using the infinite deck of aces (75%) and (25%) tens. In the EV formula of a non-aces pair split to a maximum of 2 times,
E_2 = E_0 + K*(E_1 - E_0),
I got the coefficient K = 1 + 2p-2p^2. It is neither 1+2p, nor 1 + 2p-p^2.
This also makes me think that the coefficient K in the infinite-time split case may have some problem. You used a pair of 3s vs dealer's 2 to demonstrate the derivation (E_1 stand for the EV of a pair of 3s allowing one split, and E_0 stand for the EV of a pair of 3s without splitting) and showed
E1 = (2/13) [E(soft 14) + E(5) + E_0 + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)],
but the derivation from E_1 to E_2 is still not clear to me. This part is my headache.
How did you get the coefficient K = 1 + 2p + 4p^2 - 6p^3 + 2p^4 , when a 3-time-maximum split is allowed?
link to original post
Regarding my new game with an infinite deck of 25% tens and 75% aces (where AT has an EV of 1 and all other hands have EV of 0), I get these numbers for the hand TT:
EV of standing on TT: E0 = 0
EV of splitting once: E1 = 2 EV(T hit) = 2[0.75 EV(AT) + 0.25 EV(TT stand)] = 1.5
EV of splitting up to twice: E2 = 0.75 [EV(AT) + 0.75 EV(AT) + 0.25 EV(TT split once)] + 0.25 [EV(TT split once) + EV(T hit)] = 0.75 [1 + 0.75(1) + 0.25(1.5)] + 0.25 [1.5 + 0.75] = 2.15625
Let's see which of the following formulas give 2.15625 as the EV of splitting TT up to two times:
1. E2 = E0 + (1 + 2p - p2) (E1 - E0)
2. E2 = E0 + (1 + 2p) (E1 - E0)
3. E2 = E0 + (1 + 2p - 2p2) (E1 - E0)
1. E2 = 0 + (1 + 2(0.25) - 0.252) (1.5 - 0) = 2.15625
2. E2 = 0 + (1 + 2(0.25)) (1.5 - 0) = 2.25
3. E2 = 0 + (1 + 2(0.25) - 2(0.252)) (1.5 - 0) = 2.0625
So, neither 2 nor 3 can be the correct formula, and 1 might be correct.
(In my next post, I'll show my derivation of formula 1.)
Quote: acesideQuote: ChesterDogQuote: acesideQuote: ChesterDogQuote: acesideQuote: acesideQuote: ChesterDogQuote: DJTeddyBearThanks ChesterDog.
But I've hurt my brain trying to wrap my head around your formula, specifically, to make it into an Excel calculation.
For example, the calucation the Wiz uses is = 2 * [whatever].
I substituted = ( 2 + 2/13 + (3/13)*(2/13) ) * [whatever]. This is:
2 for the original split, plus...
2/13 since there's 2 chances of matching the card, plus...
3/13 since there's 3 chances of a match of the three splits times 2/13 which is the odds that there was the original split.
Similarly, the paired tens line uses = 2 + 8/13 + (12/13)*(8/13) * [whatever].
Interestingly, this DOES change the strategy. Paired 3s vs 2 doesn't split, while paired 9s vs 7 and 10s ve 3 thru 7 all split.
It also changes the edge from 0.484% to a player advantage of 0.132%. That can't be right.
Can anybody help me figure out what I'm missing?
Thanks.
link to original post
Rather than using the complicated formula for splitting up to three times, a more instructional approach to analyzing re-splitting is first to analyze infinite re-splitting.
As an example, let's use a pair of 3s vs dealer's 2. Let E1 stand for the EV of a pair of 3s allowing one split. We know the formula for E1 is:
E1 = (2/13) [E(soft 14) + E(5) + E(6) + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
where, for example, E(6) is the EV of hitting 6 vs 2 and E(10) is the EV of doubling 10 vs 2.
The formula for the EV of a pair of 3s vs dealer's 2 allowing infinite re-splitting, Einf., is just a little different. It's:
Einf. = (2/13) [E(soft 14) + E(5) + Einf. + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
Rearranging yields:
Einf. - (2/13)Einf.= (2/13) [E(soft 14) + E(5) + 0 + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
Then:
(11/13)Einf. = (2/13) [E(soft 14) + E(5) + 0 + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
Multiplying both sides by 13/11 yields:
Einf. = (2/11) [E(soft 14) + E(5) + 0 + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
A trick to make the Excel calculations easier is to replace the 0 with E(6) - E(6), where again E(6) is the EV of hitting 6 vs 2:
Einf. = (2/11) [E(soft 14) + E(5) + E(6) + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13) - E(6)]
We can simplify the above using the fact that E1 = (2/13) [E(soft 14) + E(5) + E(6) + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]. The final result is:
Einf. = (2/11) [(13/2)E1 - E(6)] = (13/11) E1 - (2/11)E(6)
And to determine if we should split 3s vs 2, we just compare Einf. with E(6).
The above formula can be used for pairs of 2s through 9s. (Of course, we would use E(4) for 2s, for example, instead of E(6).) The formula for 10s would be a little different because the probability of getting a 10 is 4/13. And since aces cannot usually be resplit, we would just use the one-split process.
link to original post
I have followed yours and Dog Hand's instructions to get the expected results. They all seem good to me. However, to explore this a little more, I have two new questions and greatly hope you can help:
The formula for the EV of a non-aces pair split to a maximum of 2 times:
E_2 = E_0 + K*(E_1 - E_0), where K = 1 + 2p - p^2
The formula for the EV of a non-aces pair split to a maximum of 3 times:
E_3 = E_0 + K*(E_1 - E_0), where K = 1 + 2p + 4p^2 - 6p^3 + 2p^4
The formula for the EV of a non-aces pair split to a maximum of n times:
E_n = E_0 + K*(E_1 - E_0), where K= what?
The formula for the EV of a non-aces pair split to a maximum of infinite times:
E_inf = E_0 + K*(E_1 - E_0), where K = what?
link to original post
I figured out the last part myself.
The formula for the EV of a non-aces pair split to a maximum of infinite times:
E_inf = E_0 + K*(E_1 - E_0), where K = 1/(1-2p)
link to original post
Yes, I agree that K =1/(1-2p) for the infinite re-splitting formula.
By the way, I find it interesting that 1/(1-2p) = 1 + 2p + 4p2 + 8p3 + 16p4 + . . . and that the first three terms of this infinite series match those of the formula for the three-splits formula, K = 1 + 2p + 4p2 - 6p3 + 2p4
link to original post
The problem is my coefficients K’s do not match to yours. Any thoughts? Based on this math, the coefficients K’s should be:
The formula for the EV of a non-aces pair split to a maximum of 2 times:
E_2 = E_0 + K*(E_1 - E_0), where K = 1 + 2p
The formula for the EV of a non-aces pair split to a maximum of 3 times:
E_3 = E_0 + K*(E_1 - E_0), where K = 1 + 2p + 4p^2
The formula for the EV of a non-aces pair split to a maximum of n times:
E_n = E_0 + K*(E_1 - E_0), where K= 1 +2p +4p^2 +…+(2p)^n
The formula for the EV of a non-aces pair split to a maximum of infinite times:
E_inf = E_0 + K*(E_1 - E_0), where K = 1/(1-2p)
link to original post
I was thinking about our differences in the values of K on and off all today. Finally, I thought of a simple thought experiment that would help settle the problem.
Suppose we have a new game. We have an infinite deck of cards consists of 75% aces and 25% tens. Any hand of one ace and one ten is worth 1, and all other hands are worth 0.
Let's find the values of the hand TT if we stand (E0), split to a maximum of once (E1), or split to a maximum of twice (E2). Let p = the probability of pulling a ten = 0.25
Then we can compare the directly calculated value of E2 with E0 + (1 + 2p)(E1 - E0) and E0 + (1 + 2p - p2)(E1 - E0) to see if either matches.
link to original post
This problem is tricky. To verify the coefficient K, I have tried your simplified mathematical model using the infinite deck of aces (75%) and (25%) tens. In the EV formula of a non-aces pair split to a maximum of 2 times,
E_2 = E_0 + K*(E_1 - E_0),
I got the coefficient K = 1 + 2p-2p^2. It is neither 1+2p, nor 1 + 2p-p^2.
This also makes me think that the coefficient K in the infinite-time split case may have some problem. You used a pair of 3s vs dealer's 2 to demonstrate the derivation (E_1 stand for the EV of a pair of 3s allowing one split, and E_0 stand for the EV of a pair of 3s without splitting) and showed
E1 = (2/13) [E(soft 14) + E(5) + E_0 + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)],
but the derivation from E_1 to E_2 is still not clear to me. This part is my headache.
How did you get the coefficient K = 1 + 2p + 4p^2 - 6p^3 + 2p^4 , when a 3-time-maximum split is allowed?
link to original post
Below is derivation for the formula for E2, which is the EV of a pair in an infinite-deck blackjack game which allows splitting up to two times.
When a pair of 3s is split three things could happen:
1) Neither the first nor second 3 gets a 3 on its first hit.
2) The first 3 gets another 3 so the first hand can be re-split.
3) The first 3 does not get another 3, but the second 3 gets one so the second hand can be re-split.
Let p = the probability of drawing a 3. Then each of the events above have the corresponding probabilities:
1) (1 - p)2
2) p
3) (1 - p)p
The sum of probabilities is (1 - p)2 + p + (1 - p)p = 1- 2p +p2 +p + p - p2 = 1, as it should be.
The EVs of the resulting hands depend on whether a hit card after any splits can be a 3. If the hit card cannot be a 3, let's call the EV of the hand Eno. Then Eno = p[E(soft 14) + E(5) + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)] / (1 - p)
Let Eyes stand for the EV of a hand that can have 3 as a hit card. Then Eyes = p[E(soft 14) + E(5) + E(6) + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
Here's the relationship between the two EVs, by the way:
(1 - p) Eno = Eyes - pE(6) = Eyes - pE0 because E(6) is the same as E0, the EV of a pair that can not be split
The total EV of the pair allowing up to two splits is:
E2 = (1 - p)2(Eno + Eno) + p(Eyes + Eyes + Eyes) + (1-p)p(Eno + Eyes + Eyes)
Rearranging:
E2 = Eno[2(1-p)2 + (1-p)p] + Eyes[3p + 2(1-p)p]
E2 = (1-p)Eno[2(1-p) + p] + Eyes[3p + 2p - 2p2]
E2 = (1-p)Eno[2 - p] + Eyes[5p - 2p2]
E2 = (Eyes - pE0)[2 - p] + Eyes[5p - 2p2]
E2 = Eyes[2 - p + 5p - 2p2] - E0[2p - p2]
E2 = Eyes[2 + 4p - 2p2] - E0[2p - p2]
Subtracting E0 from both sides:
E2 - E0 = Eyes[2 + 4p - 2p2] - E0[1 +2p - p2]
E2 - E0 = 2Eyes[1 + 2p - p2] - E0[1 +2p - p2]
E2 - E0 = [1 + 2p - p2] (2Eyes - E0)
Since 2Eyes = E1, the EV of splitting a pair once,
E2 - E0 = [1 + 2p - p2] (E1 - E0)
The formula for the EV of a pair in an infinite-deck game allowing three splits can derived using the same method.
Quote: ChesterDogQuote: acesideQuote: ChesterDogQuote: acesideQuote: ChesterDogQuote: acesideQuote: acesideQuote: ChesterDogQuote: DJTeddyBearThanks ChesterDog.
But I've hurt my brain trying to wrap my head around your formula, specifically, to make it into an Excel calculation.
For example, the calucation the Wiz uses is = 2 * [whatever].
I substituted = ( 2 + 2/13 + (3/13)*(2/13) ) * [whatever]. This is:
2 for the original split, plus...
2/13 since there's 2 chances of matching the card, plus...
3/13 since there's 3 chances of a match of the three splits times 2/13 which is the odds that there was the original split.
Similarly, the paired tens line uses = 2 + 8/13 + (12/13)*(8/13) * [whatever].
Interestingly, this DOES change the strategy. Paired 3s vs 2 doesn't split, while paired 9s vs 7 and 10s ve 3 thru 7 all split.
It also changes the edge from 0.484% to a player advantage of 0.132%. That can't be right.
Can anybody help me figure out what I'm missing?
Thanks.
link to original post
Rather than using the complicated formula for splitting up to three times, a more instructional approach to analyzing re-splitting is first to analyze infinite re-splitting.
As an example, let's use a pair of 3s vs dealer's 2. Let E1 stand for the EV of a pair of 3s allowing one split. We know the formula for E1 is:
E1 = (2/13) [E(soft 14) + E(5) + E(6) + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
where, for example, E(6) is the EV of hitting 6 vs 2 and E(10) is the EV of doubling 10 vs 2.
The formula for the EV of a pair of 3s vs dealer's 2 allowing infinite re-splitting, Einf., is just a little different. It's:
Einf. = (2/13) [E(soft 14) + E(5) + Einf. + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
Rearranging yields:
Einf. - (2/13)Einf.= (2/13) [E(soft 14) + E(5) + 0 + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
Then:
(11/13)Einf. = (2/13) [E(soft 14) + E(5) + 0 + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
Multiplying both sides by 13/11 yields:
Einf. = (2/11) [E(soft 14) + E(5) + 0 + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
A trick to make the Excel calculations easier is to replace the 0 with E(6) - E(6), where again E(6) is the EV of hitting 6 vs 2:
Einf. = (2/11) [E(soft 14) + E(5) + E(6) + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13) - E(6)]
We can simplify the above using the fact that E1 = (2/13) [E(soft 14) + E(5) + E(6) + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]. The final result is:
Einf. = (2/11) [(13/2)E1 - E(6)] = (13/11) E1 - (2/11)E(6)
And to determine if we should split 3s vs 2, we just compare Einf. with E(6).
The above formula can be used for pairs of 2s through 9s. (Of course, we would use E(4) for 2s, for example, instead of E(6).) The formula for 10s would be a little different because the probability of getting a 10 is 4/13. And since aces cannot usually be resplit, we would just use the one-split process.
link to original post
I have followed yours and Dog Hand's instructions to get the expected results. They all seem good to me. However, to explore this a little more, I have two new questions and greatly hope you can help:
The formula for the EV of a non-aces pair split to a maximum of 2 times:
E_2 = E_0 + K*(E_1 - E_0), where K = 1 + 2p - p^2
The formula for the EV of a non-aces pair split to a maximum of 3 times:
E_3 = E_0 + K*(E_1 - E_0), where K = 1 + 2p + 4p^2 - 6p^3 + 2p^4
The formula for the EV of a non-aces pair split to a maximum of n times:
E_n = E_0 + K*(E_1 - E_0), where K= what?
The formula for the EV of a non-aces pair split to a maximum of infinite times:
E_inf = E_0 + K*(E_1 - E_0), where K = what?
link to original post
I figured out the last part myself.
The formula for the EV of a non-aces pair split to a maximum of infinite times:
E_inf = E_0 + K*(E_1 - E_0), where K = 1/(1-2p)
link to original post
Yes, I agree that K =1/(1-2p) for the infinite re-splitting formula.
By the way, I find it interesting that 1/(1-2p) = 1 + 2p + 4p2 + 8p3 + 16p4 + . . . and that the first three terms of this infinite series match those of the formula for the three-splits formula, K = 1 + 2p + 4p2 - 6p3 + 2p4
link to original post
The problem is my coefficients K’s do not match to yours. Any thoughts? Based on this math, the coefficients K’s should be:
The formula for the EV of a non-aces pair split to a maximum of 2 times:
E_2 = E_0 + K*(E_1 - E_0), where K = 1 + 2p
The formula for the EV of a non-aces pair split to a maximum of 3 times:
E_3 = E_0 + K*(E_1 - E_0), where K = 1 + 2p + 4p^2
The formula for the EV of a non-aces pair split to a maximum of n times:
E_n = E_0 + K*(E_1 - E_0), where K= 1 +2p +4p^2 +…+(2p)^n
The formula for the EV of a non-aces pair split to a maximum of infinite times:
E_inf = E_0 + K*(E_1 - E_0), where K = 1/(1-2p)
link to original post
I was thinking about our differences in the values of K on and off all today. Finally, I thought of a simple thought experiment that would help settle the problem.
Suppose we have a new game. We have an infinite deck of cards consists of 75% aces and 25% tens. Any hand of one ace and one ten is worth 1, and all other hands are worth 0.
Let's find the values of the hand TT if we stand (E0), split to a maximum of once (E1), or split to a maximum of twice (E2). Let p = the probability of pulling a ten = 0.25
Then we can compare the directly calculated value of E2 with E0 + (1 + 2p)(E1 - E0) and E0 + (1 + 2p - p2)(E1 - E0) to see if either matches.
link to original post
This problem is tricky. To verify the coefficient K, I have tried your simplified mathematical model using the infinite deck of aces (75%) and (25%) tens. In the EV formula of a non-aces pair split to a maximum of 2 times,
E_2 = E_0 + K*(E_1 - E_0),
I got the coefficient K = 1 + 2p-2p^2. It is neither 1+2p, nor 1 + 2p-p^2.
This also makes me think that the coefficient K in the infinite-time split case may have some problem. You used a pair of 3s vs dealer's 2 to demonstrate the derivation (E_1 stand for the EV of a pair of 3s allowing one split, and E_0 stand for the EV of a pair of 3s without splitting) and showed
E1 = (2/13) [E(soft 14) + E(5) + E_0 + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)],
but the derivation from E_1 to E_2 is still not clear to me. This part is my headache.
How did you get the coefficient K = 1 + 2p + 4p^2 - 6p^3 + 2p^4 , when a 3-time-maximum split is allowed?
link to original post
Below is derivation for the formula for E2, which is the EV of a pair in an infinite-deck blackjack game which allows splitting up to two times.
When a pair of 3s is split three things could happen:
1) Neither the first nor second 3 gets a 3 on its first hit.
2) The first 3 gets another 3 so the first hand can be re-split.
3) The first 3 does not get another 3, but the second 3 gets one so the second hand can be re-split.
Let p = the probability of drawing a 3. Then each of the events above have the corresponding probabilities:
1) (1 - p)2
2) p
3) (1 - p)p
The sum of probabilities is (1 - p)2 + p + (1 - p)p = 1- 2p +p2 +p + p - p2 = 1, as it should be.
The EVs of the resulting hands depend on whether a hit card after any splits can be a 3. If the hit card cannot be a 3, let's call the EV of the hand Eno. Then Eno = p[E(soft 14) + E(5) + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)] / (1 - p)
Let Eyes stand for the EV of a hand that can have 3 as a hit card. Then Eyes = p[E(soft 14) + E(5) + E(6) + E(7) + E(8) + E(9) + E(10) + E(11) + E(12) + 4E(13)]
Here's the relationship between the two EVs, by the way:
(1 - p) Eno = Eyes - pE(6) = Eyes - pE0 because E(6) is the same as E0, the EV of a pair that can not be split
The total EV of the pair allowing up to two splits is:
E2 = (1 - p)2(Eno + Eno) + p(Eyes + Eyes + Eyes) + (1-p)p(Eno + Eyes + Eyes)
Rearranging:
E2 = Eno[2(1-p)2 + (1-p)p] + Eyes[3p + 2(1-p)p]
E2 = (1-p)Eno[2(1-p) + p] + Eyes[3p + 2p - 2p2]
E2 = (1-p)Eno[2 - p] + Eyes[5p - 2p2]
E2 = (Eyes - pE0)[2 - p] + Eyes[5p - 2p2]
E2 = Eyes[2 - p + 5p - 2p2] - E0[2p - p2]
E2 = Eyes[2 + 4p - 2p2] - E0[2p - p2]
Subtracting E0 from both sides:
E2 - E0 = Eyes[2 + 4p - 2p2] - E0[1 +2p - p2]
E2 - E0 = 2Eyes[1 + 2p - p2] - E0[1 +2p - p2]
E2 - E0 = [1 + 2p - p2] (2Eyes - E0)
Since 2Eyes = E1, the EV of splitting a pair once,
E2 - E0 = [1 + 2p - p2] (E1 - E0)
The formula for the EV of a pair in an infinite-deck game allowing three splits can derived using the same method.
link to original post
This derivation is neat and the numerical verification is creative. Everything is convincing to me. Thank you for your time. I am thinking about how to apply your E_yes and E_no technique to the infinite-time split case.


