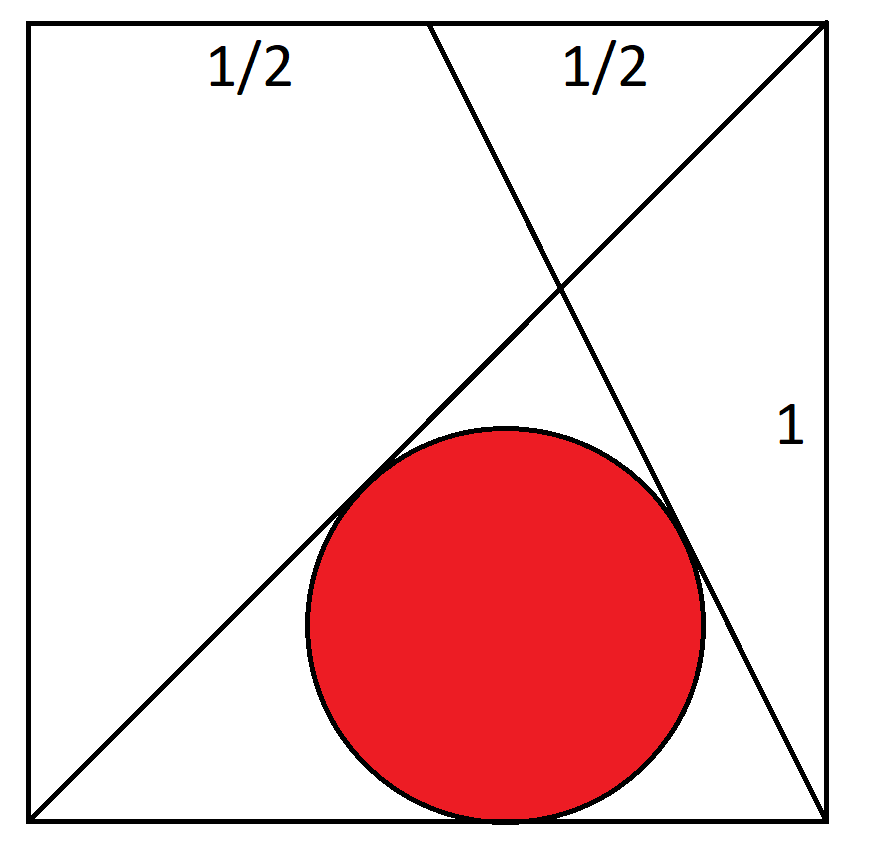
Consider the unit square with coordinates (0,0), (1,0), (1,1), (0,1). Line A goes from (0,0) to (1,1). Line B goes from (1,0) to 0.5,1). What is the radius of the circle tangent to lines A, B, and the bottom of the circle?
I'm going to dispense with the beer club rules. However, as always, please put answers and solutions in spoiler tags until an answer is correctly answered and solved.
Call angles of triangle including the circle A,B,C (CCW from lower left)
A=45 (degrees)
B=atan (2) .... B is also angle at midpoint of top for right triangle with horizontal side (1/2) and vertical right side (1)
C=180-A-B=135-B
Then
sin(A) = 1/sqrt(2)
sin(B) = 2/sqrt(5).....cos(B) = 1/sqrt(5)
sin(C) = sin(135-B)=sin(135)cos(B)-cos(135)sin(B) = 3/sqrt(10)
Call sides opposite A,B,C = a,b,c
Law of sines
a/sin(A) = b/sin(B) = c/sin(C)
c=1. .... bottom of square
b=sin(B)/sin(C) = 2sqrt(2)/3
a=sin(A)/sin(C) = sqrt(5)/3
Break sides a,b,c into two parts at the tangent point....with
x+y = c
y+z = a
x+z = b
NOTE: the two tangent segments from the triangle vertex to circle are the same by symmetry
Solve
b+c-a = (x+z)+(x+y)-(y+z)=2x
x=(b+c-a)/2 = sqrt(2)/3+1/2-sqrt(5)/6
Then bisect angle A to the center of circle and draw radius to tangent on the bottom
tan(22.5) = R/x
R = x tan(22.5)
Area = pi*R^2
=pi* ( (sqrt(2)/3+1/2-sqrt(5)/6)*tan(22.5) )^2
=0.19322152214633
Quote: Wizard...Consider the unit square with coordinates (0,0), (1,0), (1,1), (0,1). Line A goes from (0,0) to (1,1). Line B goes from (1,0) to 0.5,1). What is the radius of the circle tangent to lines A, B, and the bottom of the circle?
I'm going to dispense with the beer club rules. However, as always, please put answers and solutions in spoiler tags until an answer is correctly answered and solved.
Using vector math, I find a radius of 2 / [3 + 2sqrt(2) + sqrt(5)].
The unit vector pointing from (0,0) to (1,0) is i. And the unit vector pointing from (0,0) to (1,1) is (i + j) / sqrt(2).
Any vector in the direction from (0,0) to the center of the circle would be proportional to the sum the above two unit vectors. One such vector is M = [1+sqrt(2)]i + j.
Likewise, any vector in the direction from (1,0) to the center of the circle would be proportional to the sum of these two unit vectors: -i and (-i + 2j) / sqrt(5). One such vector would be N = [1+sqrt(5)]i - 2j. (actually this vector points in the exactly opposite direction, but it doesn't matter for the calculation.)
The position vector of the center of the circle would be the product of a constant (call it 'a') and M which is also equal to i + bN. That is: aM = i + bN.
This vector equation is equivalent to these two equations:
a[1+sqrt(2)] = 1 + b[1+sqrt(5)]
a = -2b
Substituting b = -a/2 into the first equation yields:
a[1+sqrt(2)] = 1 - a[1+sqrt(5)]/2
Dividing by a yields:
1+sqrt(2) = 1/a - [1+sqrt(5)]/2
Therefore:
1/a = 1+sqrt(2) + 1/2 + sqrt(5)/2
Or:
a = 2 / [3 + 2sqrt(2) + sqrt(5)]
And remember that the position vector of the circle's center (x,y) is aM, so y is simply a. The radius of the circle is equal to y, so r = 2 / [3 + 2sqrt(2) + sqrt(5)].
For some reason I thought it asked for area....not too Mensa-like to read the question wrong.
From my previous answer (ignoring the area calculation) I had
R=x tan (22.5)
=(sqrt(2)/3+1/2-sqrt(5)/6)*tan(22.5)
If use half angle for tan(22.5) = (1-cos(45))/sin(45) = sqrt(2) - 1
So without trig function in answer I get
R = (sqrt(2)/3+1/2-sqrt(5)/6) * (sqrt(2) - 1)
= (1+sqrt(2)+sqrt(5)-sqrt(10))/6
=0.248000646617418
Which matches Chesterdog, via calculation. Haven't figured out how my method matches it yet though.
tan(2x) = 2*tan(x)/(1-tan^2(x))
My expression for the answer is messier though. What is the method to simplifying the the following?
(sqrt(2)-1)*(2*sqrt(5)-2)/(sqrt(5) + 2*sqrt(2) - 3)
I am getting the same answer everyone else seems to be getting.
Let ABCD be the square such that A is the upper left corner and B the upper right
Let M be the midpoint of AB, X the point where BD intersects CM, and O the center of the circle
Define 2t = the measure of BDC = 45 degrees, and 2p = the measure of MCD = arctan 2
Let E be on side CD such that OE is perpendicular to CD
tan 2t = 1, so tan t = sqrt(2) - 1
tan 2p = 2, so tan p = (sqrt(5) - 1) / 2
r = x tan t = (1 - x) tan p
x (sqrt(2) - 1) = (1 - x) (sqrt(5) - 1) / 2
x = (sqrt(5) - 1) / (sqrt(5) + 2 sqrt(2) - 3)
r = x tan t = (sqrt(5) - 1) / (sqrt(5) + 2 sqrt(2) - 3) * (sqrt(2) - 1)
= (sqrt(10) - sqrt(5) - sqrt(2) + 1) / (sqrt(5) + 2 sqrt(2) - 3)
= about 0.24800065
That result can be reduced:
(sqrt(10) - sqrt(5) - sqrt(2) + 1) / (sqrt(5) + 2 sqrt(2) - 3)
= (sqrt(5) - 1) (sqrt(2) - 1) / (sqrt(5) + 2 sqrt(2) - 3)
= (sqrt(5) - 1) (sqrt(2) - 1) (sqrt(5) - (2 sqrt(2) - 3)) / ((sqrt(5) + (2 sqrt(2) - 3)) (sqrt(5) - (2 sqrt(2) - 3)))
= (sqrt(5) - 1) (sqrt(2) - 1) (sqrt(5) - 2 sqrt(2) + 3)) / (5 - (2 sqrt(2) - 3)^2)
= (sqrt(5) - 1) (sqrt(2) - 1) (sqrt(5) - 2 sqrt(2) + 3)) / (5 - 8 + 12 sqrt(2) - 9)
= (sqrt(5) - 1) (sqrt(2) - 1) (sqrt(5) - 2 sqrt(2) + 3)) / (12 (sqrt(2) - 1))
= (sqrt(5) - 1) (sqrt(2) - 1) (sqrt(2) + 1) (sqrt(5) - 2 sqrt(2) + 3)) / (12 (sqrt(2) - 1) (sqrt(2) + 1))
= (sqrt(5) - 1) (sqrt(5) - 2 sqrt(2) + 3)) / 12
= (5 - 2 sqrt(10) + 3 sqrt(5) - sqrt(5) + 2 sqrt(2) - 3) / 12
= (1 - sqrt(10) + sqrt(5) + sqrt(2)) / 6
Quote: Wizard...My expression for the answer is messier though. What is the method to simplifying the the following?
(sqrt(2)-1)*(2*sqrt(5)-2)/(sqrt(5) + 2*sqrt(2) - 3)
Not remembering having tried to simplify an expression with two different radicals in the denominator, I couldn't simplify my answer either. But just now, I see a trick--do it in two steps. First multiply the expression by [sqrt(5)-3 - 2*sqrt(2)] / [sqrt(5)-3 - 2*sqrt(2)] (which is equal to 1) and simplify.
And second, do the same procedure with a similar expression involving sqrt(5).
Quote: ChesterDogNot remembering having tried to simplify an expression with two different radicals in the denominator, I couldn't simplify my answer either. But just now, I see a trick--do it in two steps. First multiply the expression by [sqrt(5)-3 - 2*sqrt(2)] / [sqrt(5)-3 - 2*sqrt(2)] (which is equal to 1) and simplify.
And second, do the same procedure with a similar expression involving sqrt(5).
Thanks! It sticks with me from 8-th grade algebra to always abhor a radical in the denominator.
But we can also use the area formula K = rs, where r is the inradius and s is the semiperimeter. Since we have the coordinates of all three vertices, s = 1 + sqrt(5)/3 + sqrt(8)/3, and r = K/s = 2/(3+sqrt(5)+sqrt(8)).
r = 2/(3+sqrt(5)+sqrt(8)) * [3+sqrt(5)-sqrt(8)]/[3+sqrt(5)-sqrt(8)]
r = (6+4rt(2)-2rt(5)) / (12+12rt(2)) * (rt(2)-1)/(rt(2)-1)
r = (1+rt(2)+rt(5)-rt(10)) / 6
I also notice that in the "Ask the Wizard" column, the exact answer listed
Quote: rminusqI also notice that in the "Ask the Wizard" column, the exact answer listed
is incorrect, but the decimal answer is correct.(1+sqrt(2)+sqrt(5)+sqrt(50))/12
Thank you for that correction.


