Easy math puzzles

Threads: 122
Posts: 6659

Joined: Jun 22, 2011

Thanked by

September 30th, 2020 at 11:51:19 AM permalink

The distance out to sea has to take the curvature of the earth into account.

Let R be the radius of earth, and H the height of the lighthouse.
The angle t formed by the lighthouse top, the center of the earth, and the point where the light intersects the earth's surface = cos^-1 (R / (R + H))
The distance around the circumference of the earth, for angle t in radians, is t R.

In both cases, R = 4000 x 5280 feet
In the first case, H = 72 feet, t = 0.00261116113029, and the arc length = 55147.7230717332 feet
In the second case, H = 92 feet, t = 0.002951624906172, and the arc length = 62338.3180183617
The increase in beam distance = 7190.59494662844 feet

Gialmere

Threads: 45
Posts: 3044

Joined: Nov 26, 2018

September 30th, 2020 at 6:17:32 PM permalink

Quote: ThatDonGuy

The distance out to sea has to take the curvature of the earth into account.

Let R be the radius of earth, and H the height of the lighthouse.
The angle t formed by the lighthouse top, the center of the earth, and the point where the light intersects the earth's surface = cos^-1 (R / (R + H))
The distance around the circumference of the earth, for angle t in radians, is t R.

In both cases, R = 4000 x 5280 feet
In the first case, H = 72 feet, t = 0.00261116113029, and the arc length = 55147.7230717332 feet
In the second case, H = 92 feet, t = 0.002951624906172, and the arc length = 62338.3180183617
The increase in beam distance = 7190.59494662844 feet

Correct!

While math often involves intense equations (many solvable only by computers), I think it's funnest when it simplifies things to an almost comical level. Imagine a mathematician in early 1865 presenting the drawing above to the authorities...

"This circle and triangle show how to extend the range of the lighthouse beam. Point A is the center of the earth. DC is the modified lighthouse. Point B shows that sailors can now see the light around 1 1/3 miles further out to sea. So, just raise the tower by 20 feet and Bob's your uncle. Here's my bill, you may keep the drawing."

---------------------------------------

A lighthouse

Is actually very heavy.

Have you tried 22 tonight? I said 22.

Gialmere

Threads: 45
Posts: 3044

Joined: Nov 26, 2018

October 1st, 2020 at 9:14:14 AM permalink

After a severely truncated regular season, baseball has moved to a strange post season schedule. Despite the unconventional format, however, it will still end with a traditional best-of-seven World Series.

How many possible sequences are there in a World Series?

For example, one sequence would be the American League sweeping in four games.

Have you tried 22 tonight? I said 22.

ChesterDog

Threads: 9
Posts: 1702

Joined: Jul 26, 2010

Thanked by

October 1st, 2020 at 10:12:37 AM permalink

Quote: Gialmere
...
After a severely truncated regular season, baseball has moved to a strange post season schedule. Despite the unconventional format, however, it will still end with a traditional best-of-seven World Series.

How many possible sequences are there in a World Series?

For example, one sequence would be the American League sweeping in four games.

I count 70 sequences.

"A" means "American League wins the game," and "N" means "National League wins the game" in the table below:

n	Sequence
1	AAAA
2	NAAAA
3	ANAAA
4	AANAA
5	AAANA
6	NNAAAA
7	NANAAA
8	NAANAA
9	NAAANA
10	ANNAAA
11	ANANAA
12	ANAANA
13	AANNAA
14	AANANA
15	AAANNA
16	NNNAAAA
17	NNANAAA
18	NNAANAA
19	NNAAANA
20	NANNAAA
21	NANANAA
22	NANAANA
23	NAANNAA
24	NAANANA
25	NAAANNA
26	ANNNAAA
27	ANNANAA
28	ANNAANA
29	ANANNAA
30	ANANANA
31	ANAANNA
32	AANNNAA
33	AANNANA
34	AANAANA
35	AAANNNA
36	NNNN
37	ANNNN
38	NANNN
39	NNANN
40	NNNAN
41	AANNNN
42	ANANNN
43	ANNANN
44	ANNNAN
45	NAANNN
46	NANANN
47	NANNAN
48	NNAANN
49	NNANAN
50	NNNAAN
51	AAANNNN
52	AANANNN
53	AANNANN
54	AANNNAN
55	ANAANNN
56	ANANANN
57	ANANNAN
58	ANNAANN
59	ANNANAN
60	ANNNAAN
61	NAAANNN
62	NAANANN
63	NAANNAN
64	NANAANN
65	NANANAN
66	NANNAAN
67	NNAAANN
68	NNAANAN
69	NNANNAN
70	NNNAAAN

ThatDonGuy

Threads: 122
Posts: 6659

Joined: Jun 22, 2011

Thanked by

October 1st, 2020 at 11:56:28 AM permalink

Quote: ChesterDog
Quote: Gialmere
...
After a severely truncated regular season, baseball has moved to a strange post season schedule. Despite the unconventional format, however, it will still end with a traditional best-of-seven World Series.

How many possible sequences are there in a World Series?

For example, one sequence would be the American League sweeping in four games.

I count 70 sequences.

"A" means "American League wins the game," and "N" means "National League wins the game" in the table below:

n Sequence
1 AAAA
2 NAAAA
3 ANAAA
4 AANAA
5 AAANA
6 NNAAAA
7 NANAAA
8 NAANAA
9 NAAANA
10 ANNAAA
11 ANANAA
12 ANAANA
13 AANNAA
14 AANANA
15 AAANNA
16 NNNAAAA
17 NNANAAA
18 NNAANAA
19 NNAAANA
20 NANNAAA
21 NANANAA
22 NANAANA
23 NAANNAA
24 NAANANA
25 NAAANNA
26 ANNNAAA
27 ANNANAA
28 ANNAANA
29 ANANNAA
30 ANANANA
31 ANAANNA
32 AANNNAA
33 AANNANA
34 AANAANA
35 AAANNNA
36 NNNN
37 ANNNN
38 NANNN
39 NNANN
40 NNNAN
41 AANNNN
42 ANANNN
43 ANNANN
44 ANNNAN
45 NAANNN
46 NANANN
47 NANNAN
48 NNAANN
49 NNANAN
50 NNNAAN
51 AAANNNN
52 AANANNN
53 AANNANN
54 AANNNAN
55 ANAANNN
56 ANANANN
57 ANANNAN
58 ANNAANN
59 ANNANAN
60 ANNNAAN
61 NAAANNN
62 NAANANN
63 NAANNAN
64 NANAANN
65 NANANAN
66 NANNAAN
67 NNAAANN
68 NNAANAN
69 NNANNAN
70 NNNAAAN

You count correctly - and you can do it without a list.

First, count only the series where the AL team wins; each one has exactly one "partner" series where the NL wins by switching each AL win with an NL win and vice versa.
Every series ends with a win by the series-winning team, so only the games before the last one need to be considered.
4-game series have three wins and zero losses before the final win; there are Combin(3,0) = 1 ways to do this
5-game series have three wins and one loss before the final win; there are Combin(4,1) = 4 ways to do this
6-game series have three wins and two losses before the final win; there are Combin(5,2) = 10 ways to do this
7-game series have three wins and three losses before the final win; there are Combin(6,3) = 20 ways to do this
There are a total of 1 + 4 + 10 + 20 = 35 ways for the AL to win the series, so the total number of combinations = 35 x 2 = 70

Gialmere

Threads: 45
Posts: 3044

Joined: Nov 26, 2018

October 1st, 2020 at 6:38:44 PM permalink

Quote: ChesterDog
I count 70 sequences.

"A" means "American League wins the game," and "N" means "National League wins the game" in the table below:

n Sequence
1 AAAA
2 NAAAA
3 ANAAA
4 AANAA
5 AAANA
6 NNAAAA
7 NANAAA
8 NAANAA
9 NAAANA
10 ANNAAA
11 ANANAA
12 ANAANA
13 AANNAA
14 AANANA
15 AAANNA
16 NNNAAAA
17 NNANAAA
18 NNAANAA
19 NNAAANA
20 NANNAAA
21 NANANAA
22 NANAANA
23 NAANNAA
24 NAANANA
25 NAAANNA
26 ANNNAAA
27 ANNANAA
28 ANNAANA
29 ANANNAA
30 ANANANA
31 ANAANNA
32 AANNNAA
33 AANNANA
34 AANAANA
35 AAANNNA
36 NNNN
37 ANNNN
38 NANNN
39 NNANN
40 NNNAN
41 AANNNN
42 ANANNN
43 ANNANN
44 ANNNAN
45 NAANNN
46 NANANN
47 NANNAN
48 NNAANN
49 NNANAN
50 NNNAAN
51 AAANNNN
52 AANANNN
53 AANNANN
54 AANNNAN
55 ANAANNN
56 ANANANN
57 ANANNAN
58 ANNAANN
59 ANNANAN
60 ANNNAAN
61 NAAANNN
62 NAANANN
63 NAANNAN
64 NANAANN
65 NANANAN
66 NANNAAN
67 NNAAANN
68 NNAANAN
69 NNANNAN
70 NNNAAAN

Quote: ThatDonGuy

You count correctly - and you can do it without a list.

First, count only the series where the AL team wins; each one has exactly one "partner" series where the NL wins by switching each AL win with an NL win and vice versa.
Every series ends with a win by the series-winning team, so only the games before the last one need to be considered.
4-game series have three wins and zero losses before the final win; there are Combin(3,0) = 1 ways to do this
5-game series have three wins and one loss before the final win; there are Combin(4,1) = 4 ways to do this
6-game series have three wins and two losses before the final win; there are Combin(5,2) = 10 ways to do this
7-game series have three wins and three losses before the final win; there are Combin(6,3) = 20 ways to do this
There are a total of 1 + 4 + 10 + 20 = 35 ways for the AL to win the series, so the total number of combinations = 35 x 2 = 70

Correct!
-------------------------------

I couldn't figure out why the baseball kept getting larger.

Then it hit me.

Have you tried 22 tonight? I said 22.

Gialmere

Threads: 45
Posts: 3044

Joined: Nov 26, 2018

October 2nd, 2020 at 8:06:57 AM permalink

Answer the four questions below in such a way that they all have correct answers.

For each question, your answer choices are the numbers 0, 1, 2, and 3.

1) In questions 1 - 4, how many answers are 0?
2) In questions 1 - 4, how many answers are greater than 1?
3) In questions 1 - 4, how many answers are less than 2?
4) In questions 1 - 4, how many answers are 3?

Have you tried 22 tonight? I said 22.

Joeman

Joeman

Threads: 36
Posts: 2452

Joined: Feb 21, 2014

Thanked by

October 2nd, 2020 at 8:29:20 AM permalink

1) In questions 1 - 4, how many answers are 0? 1
2) In questions 1 - 4, how many answers are greater than 1? 2
3) In questions 1 - 4, how many answers are less than 2? 2
4) In questions 1 - 4, how many answers are 3? 0

"Dealer has 'rock'... Pay 'paper!'"

charliepatrick

Threads: 39
Posts: 3011

Joined: Jun 17, 2011

Thanked by

October 2nd, 2020 at 9:41:36 AM permalink

There's logic which leads to the answer

For ease assume the questions are also known as A, B, C and D

A) In questions 1 - 4, how many answers are 0?
B) In questions 1 - 4, how many answers are greater than 1?
C) In questions 1 - 4, how many answers are less than 2?
D) In questions 1 - 4, how many answers are 3?

All answers are either "greater than 1" or "less than 2"; since there are four of them B + C = 4.
If there were no zeroes, then A would have to be zero which is a contradiction. Hence there must be at least one zero somewhere and so A > 0.

If B=0 then C=4; B means there are no answers greater than 1, however C is greater than 1, so this is a contradiction.
If B=4 this contradicts the need for a zero somewhere.
Since neither B nor C can be 0 and there needs to be a 0 somewhere, it follows D must be 0. This means there are no 3's and rules out B=1 (C=3) and B=3 (C=1).

Hence B=2 C=2 D=0 and leads to A=1.

Gialmere

Threads: 45
Posts: 3044

Joined: Nov 26, 2018

October 2nd, 2020 at 7:42:35 PM permalink

Quote: Joeman
1) In questions 1 - 4, how many answers are 0? 1
2) In questions 1 - 4, how many answers are greater than 1? 2
3) In questions 1 - 4, how many answers are less than 2? 2
4) In questions 1 - 4, how many answers are 3? 0

Quote: charliepatrick
There's logic which leads to the answer
For ease assume the questions are also known as A, B, C and D

A) In questions 1 - 4, how many answers are 0?
B) In questions 1 - 4, how many answers are greater than 1?
C) In questions 1 - 4, how many answers are less than 2?
D) In questions 1 - 4, how many answers are 3?

All answers are either "greater than 1" or "less than 2"; since there are four of them B + C = 4.
If there were no zeroes, then A would have to be zero which is a contradiction. Hence there must be at least one zero somewhere and so A > 0.

If B=0 then C=4; B means there are no answers greater than 1, however C is greater than 1, so this is a contradiction.
If B=4 this contradicts the need for a zero somewhere.
Since neither B nor C can be 0 and there needs to be a 0 somewhere, it follows D must be 0. This means there are no 3's and rules out B=1 (C=3) and B=3 (C=1).

Hence B=2 C=2 D=0 and leads to A=1.

Correct!
--------------------------------

Have you tried 22 tonight? I said 22.

Wizard
Administrator

Threads: 1517
Posts: 27009

Joined: Oct 14, 2009

October 4th, 2020 at 10:34:06 PM permalink

Two points are drawn randomly on the circumference of a unit circle. What is the mean distance between them?

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

ChesterDog

Threads: 9
Posts: 1702

Joined: Jul 26, 2010

October 5th, 2020 at 4:40:23 AM permalink

Quote: Wizard
Two points are drawn randomly on the circumference of a unit circle. What is the mean distance between them?

Let the radius of the circle be 1.

Call the two random points A and B. Set up the x-axis through point A and let the minimum angle between the x-axis and the point B be called theta.

The coordinates of point A are (1,0), and the coordinates of point B are [cos(theta), sin(theta)].

The distance between points A and B is [(cos(theta)-1)²+(sin(theta))²]^1/2.

The formula for D, the mean value of the distance between points A and B is:
D = integral from 0 to pi of [(cos(theta)-1)²+(sin(theta))²]^1/2d(theta) / integral from 0 to pi of d(theta).

This simplifies to D = (1/pi) * integral from 0 to pi of [2-2cos(theta)]^1/2d(theta).

The above can be rearranged to D = (2/pi) * integral from 0 to pi of [(1-cos(theta))/2]^1/2 d(theta).
Using a �half-angle formula,� sin(theta/2) = [1-cos(theta/2))/2]^1/2, this becomes: D = (2/pi) * integral from 0 to pi of sin(theta/2) d(theta).

Letting u = theta/2, the integral from 0 to pi of sin(theta/2) d(theta) becomes the integral from 0 to pi/2 of 2sin(u) du, which equals 2.

Therefore, D = 4/pi. For a circle of radius r, the average distance between two random points would be 4r/pi.

Wizard
Administrator

Threads: 1517
Posts: 27009

Joined: Oct 14, 2009

October 5th, 2020 at 7:39:43 AM permalink

Quote: ChesterDog

Let the radius of the circle be 1.

Call the two random points A and B. Set up the x-axis through point A and let the minimum angle between the x-axis and the point B be called theta.

The coordinates of point A are (1,0), and the coordinates of point B are [cos(theta), sin(theta)].

The distance between points A and B is [(cos(theta)-1)²+(sin(theta))²]^1/2.

The formula for D, the mean value of the distance between points A and B is:
D = integral from 0 to pi of [(cos(theta)-1)²+(sin(theta))²]^1/2d(theta) / integral from 0 to pi of d(theta).

This simplifies to D = (1/pi) * integral from 0 to pi of [2-2cos(theta)]^1/2d(theta).

The above can be rearranged to D = (2/pi) * integral from 0 to pi of [(1-cos(theta))/2]^1/2 d(theta).
Using a �half-angle formula,� sin(theta/2) = [1-cos(theta/2))/2]^1/2, this becomes: D = (2/pi) * integral from 0 to pi of sin(theta/2) d(theta).

Letting u = theta/2, the integral from 0 to pi of sin(theta/2) d(theta) becomes the integral from 0 to pi/2 of 2sin(u) du, which equals 2.

Therefore, D = 4/pi. For a circle of radius r, the average distance between two random points would be 4r/pi.

Correct!

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

Gialmere

Threads: 45
Posts: 3044

Joined: Nov 26, 2018

October 5th, 2020 at 3:51:08 PM permalink

Cee-lo is an Asian gambling game played with three standard dice. When played without a banker, players ante an agreed to amount and then take turns rolling the dice with the high roll winning the pot.

A dice roll yields the following results...

4-5-6: Called a Cee-lo, this straight is the highest roll you can make.

Trips: A higher number three-of-a-kind beats a lower number, but any trips beats a point number.

Point Number: If you roll a pair, the singleton becomes your point number, the higher the better. Thus a 2-2-5 has a point value of 5 and beats a 5-5-2 which is worth only 2.

1-2-3: This straight is the worst roll you can get and loses to all the rolls above.

Any other roll is a meaningless combination and must be rerolled until one of the above combinations occurs.

What is the probability that the dice will have to be rerolled?

Have you tried 22 tonight? I said 22.

ThatDonGuy

Threads: 122
Posts: 6659

Joined: Jun 22, 2011

Thanked by

October 5th, 2020 at 5:48:35 PM permalink

The rolls that do not require a reroll are:
1,2,3 - there are 6 ways to roll this
4,5,6 - there are also 6 ways to roll this
Any triple - there are 6 triples, each of which has 1 way to roll, for a total of 6
Any pair - there are 6 pairs; for each one, there are 5 values for the point, and 3 ways to roll each pair/point combination, for a total of 90

This is a total of 108 rolls that do not require a reroll, so there are 216 - 108 = 108 that do, and the probability of a reroll = 108 / 216 = 1/2

Gialmere

Threads: 45
Posts: 3044

Joined: Nov 26, 2018

October 5th, 2020 at 6:24:38 PM permalink

Quote: ThatDonGuy

The rolls that do not require a reroll are:
1,2,3 - there are 6 ways to roll this
4,5,6 - there are also 6 ways to roll this
Any triple - there are 6 triples, each of which has 1 way to roll, for a total of 6
Any pair - there are 6 pairs; for each one, there are 5 values for the point, and 3 ways to roll each pair/point combination, for a total of 90

This is a total of 108 rolls that do not require a reroll, so there are 216 - 108 = 108 that do, and the probability of a reroll = 108 / 216 = 1/2

Correct!
------------------------------

Have you tried 22 tonight? I said 22.

Gialmere

Threads: 45
Posts: 3044

Joined: Nov 26, 2018

October 6th, 2020 at 8:18:49 AM permalink

Place a king, a queen, a rook, a knight, and a bishop on a 4 x 4 chessboard so that no piece attacks another.

Have you tried 22 tonight? I said 22.

Joeman

Joeman

Threads: 36
Posts: 2452

Joined: Feb 21, 2014

Thanked by

October 6th, 2020 at 8:42:09 AM permalink

---------
| |r| | |
---------
| | | |k|
---------
|q| | | |
---------
| | |b|n|
---------

"Dealer has 'rock'... Pay 'paper!'"

unJon

unJon

Threads: 16
Posts: 4756

Joined: Jul 1, 2018

October 6th, 2020 at 9:06:43 AM permalink

Nevermind

The race is not always to the swift, nor the battle to the strong; but that is the way to bet.

ThatDonGuy

Threads: 122
Posts: 6659

Joined: Jun 22, 2011

Thanked by

October 6th, 2020 at 10:09:35 AM permalink

Using a brute force search, I get just these two:

*	K	*	N
*	*	*	B
Q	*	*	*
*	*	R	*

*	K	*	N
*	*	*	B
R	*	*	*
*	*	Q	*

charliepatrick

Threads: 39
Posts: 3011

Joined: Jun 17, 2011

Thanked by

October 6th, 2020 at 1:06:49 PM permalink

(i) The Rook and Bishop cannot be adjacent (otherwise one could take the other)
(ii) The King cannot be adjacent to any other piece
The Queen can only be in three logical positions, all the others are a mirror or rotation equivalent.

\	?	\|	?
?	\	\|	/
-	-	Q	-
?	/	\|	\

All the remaining positions the Knight can take the Queen

\	?	?	\|
k	\	?	\|
k	k	\	\|
-	-	-	Q

The King eliminates three squares, so there's no room for the Rook/Bishop pair.

N1	N2	*	N3
*		*
	*	*	*
*	*	Q	*

Three positions for the Knight, let's look at each one.

N	B	*
*		*	R
K	*	*	*
*	*	Q	*

N1: This forces the Rook to be in the second row, but LHS option cannot fit K/B.

	N	*	k
*		*	k
	*	*	*
*	*	Q	*

N2: This forces the King to the RHS, now the R/B have nowhere to go.

	K	*	N
*		*	B
R	*	*	*
*	*	Q	*

N3: If the King was in the second/third row the R cannot be played), hence K in first row and only where R can be played.

Gialmere

Threads: 45
Posts: 3044

Joined: Nov 26, 2018

October 6th, 2020 at 6:45:01 PM permalink

Quote: Joeman

---------
| |r| | |
---------
| | | |k|
---------
|q| | | |
---------
| | |b|n|
---------

Quote: ThatDonGuy

Using a brute force search, I get just these two:
* K * N
* * * B
Q * * *
* * R *

* K * N
* * * B
R * * *
* * Q *

Quote: charliepatrick
(i) The Rook and Bishop cannot be adjacent (otherwise one could take the other)
(ii) The King cannot be adjacent to any other piece
The Queen can only be in three logical positions, all the others are a mirror or rotation equivalent.

\ ? | ?
? \ | /
- - Q -
? / | \

All the remaining positions the Knight can take the Queen

\ ? ? |
k \ ? |
k k \ |
- - - Q

The King eliminates three squares, so there's no room for the Rook/Bishop pair.

N1 N2 * N3
* *
* * *
* * Q *

Three positions for the Knight, let's look at each one.

N B *
* * R
K * * *
* * Q *

N1: This forces the Rook to be in the second row, but LHS option cannot fit K/B.

N * k
* * k
* * *
* * Q *

N2: This forces the King to the RHS, now the R/B have nowhere to go.

K * N
* * B
R * * *
* * Q *

N3: If the King was in the second/third row the R cannot be played), hence K in first row and only where R can be played.

Correct!

Heh, thanks to the excellent responses there's no reason to post this picture but, since I'm already hosting it, here it is.

Yes, the rook and queen can swap spots.

--------------------------------

Have you tried 22 tonight? I said 22.

Gialmere

Threads: 45
Posts: 3044

Joined: Nov 26, 2018

October 7th, 2020 at 8:31:28 AM permalink

This classic puzzle is now more than 100 years old...

ABC is an isosceles triangle in which AB = AC and angle A = 20°.

BD is a line segment intersecting angle B, such that angle DBC = 70°.

A line segment CE intersects angle C, such that angle ECB = 60°.

ED is Joined.

Determine the measure of angle EDB.

Have you tried 22 tonight? I said 22.

ThatDonGuy

Threads: 122
Posts: 6659

Joined: Jun 22, 2011

Thanked by

October 8th, 2020 at 12:29:10 PM permalink

I am fairly confident the answer is 20 degrees

However, proving this has proven elusive. The closest I have gotten is this:

EDB = arcsin( sqrt( (1 - sin^2 70) / (1 - 8 sin 10 sin^2 70 + 16 sin^2 10 sin^2 70) ) ) - 30 degrees

charliepatrick

Threads: 39
Posts: 3011

Joined: Jun 17, 2011

Thanked by

October 8th, 2020 at 8:43:40 PM permalink

You can solve this without resorting to Sine's etc but will need to add a few lines to the diagram, i.e. "proof by construction"

I think most people can work out the angles without construction and that's when one gets stuck. The trick seems to be to add a few more lines and prove that triangles are isosceles.

Triangle(ABC) is isosceles. ABC=ACB=80 (180-20)/2.
Construct BG which is a mirror image of EC.
GBC=60, so ABG=20, so Triangle(ABG) is isosceles, so AG=BG.
BFC is equilateral (as two of its angles are 60), similarly EFG is 60 so EFG is equilateral. So EG=FG.
Construct AF (as BFC is equilateral, F is along the middle line.)
Consider triangles AFG and BDG. They are congruent (angles are 10 30 140 and AG=BG). So FG=GD.
So DG=EG. So EGD is isosceles with EGD=80 (=BCA). So the other two angles are 50.
Consider the triangle BCD (70 80 30) so BDC=30.
EDG=50, so EDB=20.

Summary: you contruct an equilateral triangle EFG and consider Tr(AFG)=Tr(BDG) to show Tr(EGD) is isosceles and EDG=50. This gives EDB=20.

Gialmere

Threads: 45
Posts: 3044

Joined: Nov 26, 2018

October 8th, 2020 at 8:46:08 PM permalink

Quote: ThatDonGuy

I am fairly confident the answer is 20 degrees

However, proving this has proven elusive. The closest I have gotten is this:

EDB = arcsin( sqrt( (1 - sin^2 70) / (1 - 8 sin 10 sin^2 70 + 16 sin^2 10 sin^2 70) ) ) - 30 degrees

Yes. This one has been been called "the hardest easy math puzzle". You're right on top of it though. We'll let it ride a little longer.

Have you tried 22 tonight? I said 22.

Gialmere

Threads: 45
Posts: 3044

Joined: Nov 26, 2018

October 8th, 2020 at 10:51:18 PM permalink

Quote: charliepatrick
You can solve this without resorting to Sine's etc but will need to add a few lines to the diagram, i.e. "proof by construction"
I think most people can work out the angles without construction and that's when one gets stuck. The trick seems to be to add a few more lines and prove that triangles are isosceles.

Triangle(ABC) is isosceles. ABC=ACB=80 (180-20)/2.
Construct BG which is a mirror image of EC.
GBC=60, so ABG=20, so Triangle(ABG) is isosceles, so AG=BG.
BFC is equilateral (as two of its angles are 60), similarly EFG is 60 so EFG is equilateral. So EG=FG.
Construct AF (as BFC is equilateral, F is along the middle line.)
Consider triangles AFG and BDG. They are congruent (angles are 10 30 140 and AG=BG). So FG=GD.
So DG=EG. So EGD is isosceles with EGD=80 (=BCA). So the other two angles are 50.
Consider the triangle BCD (70 80 30) so BDC=30.
EDG=50, so EDB=20.

Summary: you contruct an equilateral triangle EFG and consider Tr(AFG)=Tr(BDG) to show Tr(EGD) is isosceles and EDG=50. This gives EDB=20.

Correct!

This problem is essentially Langley's Adventitious Angles. Over the years, several ways have been discovered to solve it.

-------------------------------

Have you tried 22 tonight? I said 22.

Gialmere

Threads: 45
Posts: 3044

Joined: Nov 26, 2018

October 9th, 2020 at 8:16:02 AM permalink

Math Trick
1) Pick any number
2) Multiply the number by 6
3) Add_________
4) Divide by __________
5) Subtract the number you started with

Complete 3 & 4 so that the expected outcome will always be 7.

Have you tried 22 tonight? I said 22.

charliepatrick

Threads: 39
Posts: 3011

Joined: Jun 17, 2011

Thanked by

October 9th, 2020 at 9:25:03 AM permalink

Add 42, Divide by 6
Method 1
(6x+a)/d-x = 6x/d - x + a/d.
For this to be independent of x 6x/d-x has to be zero for all x. This means 6/d=1; i.e. d=6.
What's left is a/d = a/6. This has to equal 7, so a=42.

Method 2
Start with (6x+a)/d-x and plug in a few values for x knowing the result needs to be 7.
x=0 gives a/d=7.
x=1 leads to (6+a)/d-1 = 6/d + a/d - 1 = 6/d + 7 - 1 = 7. Hence 6/d-1=0 so d=6, then a=42.

Ace2

Ace2

Threads: 32
Posts: 2706

Joined: Oct 2, 2017

October 9th, 2020 at 5:49:19 PM permalink

If you roll a standard die 6,000 times, what is the probability that all six values are equally distributed (meaning 1,000 ones, twos, threes, fours, fives, and sixes are rolled)?

An accurate estimate is acceptable for this problem

It�s all about making that GTA

Gialmere

Threads: 45
Posts: 3044

Joined: Nov 26, 2018

October 9th, 2020 at 10:33:02 PM permalink

Quote: charliepatrick
Add 42, Divide by 6
Method 1
(6x+a)/d-x = 6x/d - x + a/d.
For this to be independent of x 6x/d-x has to be zero for all x. This means 6/d=1; i.e. d=6.
What's left is a/d = a/6. This has to equal 7, so a=42.

Method 2
Start with (6x+a)/d-x and plug in a few values for x knowing the result needs to be 7.
x=0 gives a/d=7.
x=1 leads to (6+a)/d-1 = 6/d + a/d - 1 = 6/d + 7 - 1 = 7. Hence 6/d-1=0 so d=6, then a=42.

Correct!
-------------------------------

When I was a student I asked my algebra teacher, "When am I ever gonna use this?"

"Well you won't," he replied cheerfully, "but one of the smart kids might."

Have you tried 22 tonight? I said 22.

ChesterDog

Threads: 9
Posts: 1702

Joined: Jul 26, 2010

October 10th, 2020 at 12:51:13 AM permalink

Quote: Ace2
If you roll a standard die 6,000 times, what is the probability that all six values are equally distributed (meaning 1,000 ones, twos, threes, fours, fives, and sixes are rolled)?

An accurate estimate is acceptable for this problem

The total number of permutations of 1000 each of ones, twos, threes, fours, fives, and sixes is: 6000! / (1000!)⁶.

The total number of outcomes of 6000 rolls of a die is: 6⁶⁰⁰⁰.

So, the probability p of an equal distribution is: p = 6000! / [ (1000!)⁶ (6⁶⁰⁰⁰) ]

Taking natural log of both sides gives: ln(p) = ln(6000!) - 6ln(1000!) - 6000ln(6)

We can then use the Wizard's calculator to get an approximate numerical answer: p = 7.8237477 x 10^-10

Wizard
Administrator

Threads: 1517
Posts: 27009

Joined: Oct 14, 2009

October 10th, 2020 at 3:05:50 AM permalink

Quote: Ace2
If you roll a standard die 6,000 times, what is the probability that all six values are equally distributed (meaning 1,000 ones, twos, threes, fours, fives, and sixes are rolled)?

An accurate estimate is acceptable for this problem

(6000!/((1000!)^6))*(1/6)^6000 = 0.0000000007823747736781498210063883739136884170894229348659701176719666057318180767055573907778623822085474829477790013705722134575306117609409880363078025249483640817615245431932589600987224590433738858031106665646147517585321499054231528356717293330747094170389035.

However, I think the better question is what is a way to get a close approximation without the need of a super calculator like the WizCalc. I've worked out my own approximation, but its about 2.12 times too large. At least in the ballpark, but I should be able to do better.

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

Wizard
Administrator

Threads: 1517
Posts: 27009

Joined: Oct 14, 2009

October 10th, 2020 at 7:28:16 AM permalink

Let's use the Gaussian curve to find the probability of getting exactly 1000 ones. The standard deviation is sqrt(6000*(1/6)*(5/6)) = 28.86751346. The expected number of ones is obviously 1,000.

My estimate is going to be the probability of getting 999.5 to 1000.5 on the bull curve. I won't go through all the steps, but my answer comes to 0.013819075.

Taking that to the fifth power we get 5.03959E-10. This is 64% of the exact answer I already gave.

I previously took sqrt(5000*(1/5)*(4/5)) for the number of twos, and so on down, but that answer came to 1.655871E-09, 2.12 times too large.

At this point, I'm out of ideas how to do this properly.

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

Ace2

Ace2

Threads: 32
Posts: 2706

Joined: Oct 2, 2017

October 10th, 2020 at 7:48:43 AM permalink

Chesterdog and Wizard, that is the correct exact answer.

Use Stirling's formula (n/e)^n * (2πn)^.5 for very accurate estimates of the factorials.

When you substitute it into the exact formula 6000!/((1000!)^6 * 6^6000), terms cancel nicely to get:

6^.5 / (2π1000)^2.5 = 7.8276 * 10^-10

Within 0.05% of the exact answer

Last edited by: Ace2 on Oct 10, 2020

It�s all about making that GTA

ThatDonGuy

Threads: 122
Posts: 6659

Joined: Jun 22, 2011

October 10th, 2020 at 7:53:57 AM permalink

Quote: Ace2
If you roll a standard die 6,000 times, what is the probability that all six values are equally distributed (meaning 1,000 ones, twos, threes, fours, fives, and sixes are rolled)?

An accurate estimate is acceptable for this problem

There are Combin(6000, 1000) ways to select the 1000 1s, Combin(5000, 1000) ways to select the 1000 2s, and so on, through Combin(1000, 6000) = 1 way to choose the 1000 6s.
The solution is Combin(6000, 1000) x Combin(5000, 1000) x Combin(4000, 1000) x Combin(3000, 1000) x Combin(2000, 1000) / 6^6000 =
1,795,052,805,219,784,723,242,975,837,221,741,255,578,886,657,468,818,089,209,063,431,492,440,933
,063,351,076,093,658,704,313,523,176,728,635,427,017,435,620,586,466,262,821,008,505,814,958,473,278
,874,171,764,145,026,379,616,580,620,746,294,392,109,840,919,608,250,871,016,524,736,682,213,262,327
,103,972,413,909,286,386,278,476,350,195,790,515,074,537,177,427,178,639,199,543,965,439,310,972,900
,080,995,237,293,648,433,171,054,450,156,959,727,397,257,092,230,826,556,209,497,066,043,681,160,970
,382,038,060,953,127,950,234,931,165,018,702,661,139,443,203,547,490,039,196,227,274,925,331,640,784
,861,536,941,581,523,588,664,388,648,966,136,719,926,363,672,079,741,402,174,875,863,199,332,510,249
,371,822,234,852,905,496,550,632,095,803,256,726,037,798,935,325,933,380,977,529,237,337,864,891,908
,971,555,370,971,686,889,109,778,161,636,552,572,169,456,081,983,983,003,392,444,800,283,122,009,580
,922,365,461,809,602,916,864,168,695,745,747,083,636,018,237,303,215,508,291,721,521,415,216,524,299
,249,643,471,487,966,216,995,711,721,468,115,704,270,386,476,664,386,995,762,680,465,488,243,061,759
,564,004,353,504,024,049,690,483,737,657,871,705,426,122,652,617,465,098,495,791,458,244,965,336,570
,753,039,763,053,592,329,766,182,600,168,616,994,028,032,972,637,205,631,403,567,837,062,702,773,339
,295,484,183,046,849,345,496,585,933,539,373,519,779,178,938,884,021,747,951,683,615,251,641,032,889
,170,126,978,631,374,697,791,334,793,089,614,999,400,959,912,526,813,097,980,654,025,300,105,494,182
,747,966,181,510,150,842,325,462,205,708,709,894,566,351,924,358,096,259,887,130,523,048,729,080,350
,865,253,957,841,472,433,557,219,327,978,236,062,982,266,838,181,687,059,813,119,046,789,855,508,890
,702,295,214,476,885,257,534,319,044,699,878,833,776,075,097,458,540,310,320,098,905,611,964,994,909
,968,960,716,477,209,459,424,835,050,713,674,549,804,118,077,423,074,096,854,671,540,387,167,660,631
,965,029,933,834,978,648,045,444,506,484,213,859,301,172,229,097,865,413,833,394,867,962,978,530,738
,320,410,759,821,373,622,196,199,322,274,780,389,005,600,845,350,378,166,448,808,618,449,968,077,246
,974,770,676,858,820,772,578,856,490,973,004,538,174,734,939,253,930,408,015,798,238,789,166,272,813
,825,864,182,552,554,624,211,247,130,926,540,448,701,191,023,564,160,627,499,514,192,447,701,146,264
,300,115,252,294,003,496,877,597,453,992,726,839,280,361,248,614,827,228,427,394,874,088,125,854,587
,195,766,565,043,674,507,602,962,201,640,602,434,419,617,895,507,594,037,343,060,035,607,650,243,545
,280,982,926,897,869,829,227,080,572,984,217,857,267,700,104,917,671,493,025,901,043,713,466,267,883
,826,049,647,963,528,492,590,402,719,436,526,051,062,528,136,937,177,631,458,403,212,861,826,004,345
,694,666,640,635,199,170,208,649,811,563,803,009,356,675,253,904,983,387,222,839,595,227,797,595,045
,592,443,007,821,739,704,738,601,863,471,916,696,224,309,689,043,255,813,232,209,667,878,246,371,938
,942,854,268,899,315,852,428,071,314,745,796,905,318,738,458,934,731,366,874,742,641,803,112,712,843
,260,091,892,155,391,425,184,282,182,514,266,706,209,786,161,068,231,599,224,601,152,080,056,205,765
,611,079,000,148,195,992,223,235,222,757,555,768,703,588,198,465,941,598,040,980,095,174,006,293,703
,316,804,135,209,867,851,680,087,172,487,990,677,874,794,332,713,978,887,906,684,570,236,908,183,051
,590,497,254,590,472,896,683,229,484,959,673,773,560,618,760,194,942,389,607,840,412,752,044,061,768
,948,838,028,774,907,905,860,326,770,481,322,654,234,629,348,716,017,266,987,100,404,702,057,582,517
,955,454,604,295,520,045,581,289,657,844,916,716,981,326,391,230,125,994,687,068,915,768,296,956,173
,469,235,118,622,375,961,476,639,180,219,966,622,512,276,034,667,489,642,929,615,743,500,917,165,777
,664,743,737,463,547,793,107,773,235,642,415,821,848,019,711,392,739,868,546,021,026,647,602,036,193
,403,011,319,400,461,376,855,716,340,418,747,787,870,915,289,067,616,486,143,615,596,030,218,576,117
,787,318,417,447,165,623,174,052,125,853,207,073,751,057,259,611,729,868,945,671,616,806,653,349,068
,639,216,147,360,539,471,661,857,002,970,621,854,698,544,508,422,259,035,116,481,084,612,240,501,135
,874,095,227,220,156,103,795,396,593,383,526,340,916,024,094,304,635,596,919,714,679,939,836,144,409
,176,968,693,221,352,384,580,320,898,081,696,876,282,236,990,309,049,993,013,754,184,583,397,369,942
,360,915,338,206,124,544,657,854,772,680,068,320,360,946,069,699,010,136,298,710,837,280,581,327,757
,778,717,376,020,246,392,857,646,416,711,185,480,395,233,853,699,070,256,448,888,131,589,607,431,606
,066,759,842,808,559,254,158,247,971,084,341,198,580,578,176,928,567,374,578,890,428,248,009,091,111
,147,973,242,521,929,686,395,309,954,504,161,345,205,443,457,212,215,245,629,259,135,555,020,928,841
,974,558,913,761,230,921,038,524,198,368,040,382,179,717,659,052,015,164,200,725,772,076,314,493,515
,360,363,521,847,871,782,469,602,644,858,118,161,526,588,690,719,814,162,707,660,949,506,820,819,816
,970,395,150,869,306,741,377,248,663,585,195,810,913,823,283,063,892,822,962,436,093,581,375,237,138
,794,866,933,635,832,040,165,953,216,292,142,634,000,549,119,687,027,125,427,843,721,303,953,151,283
,484,772,952,888,068,841,767,768,412,404,924,082,086,377,010,222,280,100,947,084,294,888,644,449,584
,323,630,715,451,742,626,905,116,905,129,578,194,862,176,271,254,240,028,177,241,643,275,951,659,585
,441,789,652,780,868,967,038,402,407,039,517,395,418,857,647,459,000,994,750,459,944,724,976,340,904
,261,376,453,152,492,895,436,334,628,505,655,003,409,040,914,100,263,786,105,221,578,625,372,147,887
,224,546,419,185,459,691,268,408,910,546,752,288,230,225,709,692,320,682,488,633,817,282,777,466,949
,793,386,676,651,702,120,682,578,275,035,302,664,213,713,042,280,838,788,028,441,977,168,950,806,031
,783,490,149,247,521,075,765,692,549,170,831,164,703,273,687,473,652,445,727,096,649,148,180,559,893
,268,917,397,636,681,853,525,361,061,797,745,185,901,957,681,083,131,070,013,858,247,180,971,346,110
,747,119,354,088,233,897,514,539,254,898,253,131,221,037,649,035,508,755,076,900,164,394,619,671,440
,505,241,089,214,150,819,638,842,202,986,137,618,800,209,450,503,066,883,380,616,630,531,149,178,335
,387,127,888,647,203,788,022,265,764,829,788,530,746,985,573,265,667,015,619,966,195,734,566,116,875
divided by
2,294,364
,370,646,523,818,790,870,954,810,989,650,594,858,883,840,712,601,381,705,390,459,585,009,431,253,970
,242,941,614,593,281,399,604,519,581,846,083,543,476,829,251,419,237,401,641,666,407,566,099,559,732
,468,223,470,502,558,252,002,665,153,971,898,943,364,275,789,825,256,872,379,522,588,650,801,204,676
,850,794,132,068,955,798,938,381,816,611,078,964,815,072,660,304,095,541,069,053,986,493,598,874,491
,342,510,612,985,971,431,462,543,237,248,021,156,944,940,609,301,553,666,215,912,379,309,947,792,656
,552,129,300,439,510,712,449,002,420,594,472,026,667,264,847,404,795,920,305,296,286,858,917,060,685
,361,301,807,806,798,660,961,174,340,674,570,829,927,924,685,429,168,764,151,971,408,532,409,090,711
,273,493,011,521,064,644,512,940,783,244,175,770,654,199,439,364,426,677,058,986,401,671,965,898,765
,037,019,959,852,602,263,087,846,738,198,089,151,713,962,176,541,955,560,616,310,153,538,163,424,977
,481,892,177,938,273,820,249,357,426,643,432,059,665,405,003,386,889,457,468,156,123,807,497,050,693
,804,694,645,960,158,154,388,019,860,380,813,258,580,556,236,230,885,704,642,050,640,280,949,531,661
,987,655,405,014,495,943,859,289,116,214,125,321,474,758,681,653,510,538,719,669,334,144,124,540,424
,686,276,547,584,075,510,185,896,284,355,919,112,636,327,972,714,794,278,233,146,030,881,510,056,104
,535,273,497,209,839,163,441,859,780,547,979,186,083,965,617,505,919,475,633,682,280,187,377,135,338
,129,382,382,169,368,100,701,260,993,084,381,833,947,812,102,061,184,947,907,887,339,117,489,343,771
,706,828,447,216,873,937,538,836,501,957,244,544,328,229,233,309,593,890,206,399,966,655,266,958,553
,065,110,907,809,604,173,842,359,527,313,578,733,929,671,931,408,052,083,090,751,907,044,755,564,267
,559,158,037,406,160,129,166,889,769,394,203,843,381,972,972,421,192,887,553,899,805,863,925,754,874
,612,519,029,964,572,508,969,874,502,886,461,459,164,970,220,741,969,986,922,976,358,799,668,006,232
,558,063,149,778,015,757,799,638,137,136,221,044,010,301,653,412,279,493,697,364,740,038,695,889,270
,602,027,633,119,676,449,326,515,924,927,561,356,111,755,297,145,291,581,046,904,867,047,115,845,999
,283,217,284,810,764,329,520,023,517,370,488,931,340,758,015,248,162,203,021,009,031,464,969,769,602
,995,022,963,837,388,571,869,545,489,131,623,811,195,535,381,931,057,740,849,920,083,068,146,829,160
,061,978,998,246,575,885,215,174,135,491,437,811,885,208,781,773,740,909,018,311,001,714,701,072,126
,182,856,935,239,535,814,987,975,923,962,184,767,756,462,008,355,060,897,242,425,469,189,375,156,263
,453,070,276,327,794,112,251,993,104,782,024,487,878,195,033,776,015,630,900,126,867,447,084,690,527
,616,919,366,637,595,529,114,212,998,849,900,398,010,720,163,930,009,043,153,566,737,830,671,652,974
,601,406,352,043,041,334,756,422,769,840,516,147,179,464,762,959,785,898,744,437,558,923,387,862,619
,072,174,294,554,879,976,268,062,095,392,370,746,480,569,631,923,408,525,670,383,424,312,296,176,858
,877,496,684,598,292,468,955,795,052,357,414,239,903,903,551,192,081,712,283,449,069,442,356,735,931
,176,441,516,525,606,907,347,760,670,040,094,512,155,867,965,098,604,098,256,289,852,701,168,416,529
,185,365,724,655,523,995,489,288,804,737,273,275,999,570,938,469,390,288,687,326,582,299,462,125,901
,548,872,696,700,494,084,645,456,629,270,674,255,478,495,380,598,403,819,876,143,198,317,506,839,912
,984,247,832,547,840,241,312,098,933,415,199,933,833,404,873,809,741,077,324,457,795,562,678,557,639
,856,264,516,334,520,341,094,512,637,606,825,679,295,374,137,388,330,624,473,869,555,865,861,430,527
,358,001,768,512,766,974,973,453,677,937,442,975,084,661,389,103,117,053,572,900,339,231,053,674,196
,519,007,745,371,506,229,009,161,008,855,527,610,479,516,221,469,908,117,019,243,814,704,103,761,461
,195,425,814,000,083,176,201,845,974,663,903,023,566,436,196,997,540,548,016,192,043,972,963,291,371
,302,020,012,542,195,671,198,027,651,891,726,351,156,593,973,529,194,251,802,362,266,416,898,325,412
,984,454,188,750,759,471,962,864,326,641,951,450,165,990,672,487,611,411,471,405,533,146,384,281,286
,665,224,480,848,908,374,557,981,229,877,292,476,890,488,879,405,124,276,657,046,672,462,508,951,681
,817,903,645,331,724,148,785,760,921,738,582,612,776,236,478,777,495,029,612,329,968,376,188,712,707
,746,440,279,176,582,384,507,241,505,369,129,364,529,391,373,506,707,384,007,812,689,256,059,672,412
,930,602,196,552,171,832,793,637,435,023,486,425,094,160,124,064,277,641,370,539,182,383,072,641,473
,512,694,276,558,363,548,424,314,577,033,853,058,072,696,915,862,458,170,177,828,720,666,654,611,488
,152,117,870,731,085,690,435,700,091,336,300,861,513,526,034,379,234,516,662,679,569,661,161,815,449
,117,120,092,146,642,112,566,724,266,189,929,029,251,883,305,486,595,712,095,018,271,143,860,992,134
,015,891,671,384,110,922,058,607,325,350,063,403,805,458,360,336,890,283,011,462,426,859,321,414,995
,432,313,141,584,480,567,819,816,173,319,814,354,067,751,614,547,737,244,006,433,752,723,069,392,895
,955,540,968,516,929,306,896,477,734,220,418,287,073,028,409,223,696,795,407,226,470,170,159,781,713
,184,667,188,005,727,850,992,634,336,069,936,348,820,992,203,675,244,937,539,510,933,302,366,013,930
,519,166,968,936,521,319,715,058,249,225,146,145,987,462,780,594,243,255,934,980,688,442,535,956,923
,051,472,117,629,433,776,465,493,125,991,479,563,186,051,977,030,131,601,601,483,398,420,351,716,575
,223,120,668,777,765,778,655,614,058,334,207,934,072,405,992,606,842,907,635,164,942,532,529,299,631
,403,255,009,691,526,187,892,720,507,416,083,572,554,684,914,849,581,302,374,335,653,015,044,541,319
,275,980,509,024,594,440,013,389,464,606,085,583,656,098,720,837,639,113,319,073,731,058,795,014,461
,921,696,754,177,910,427,272,340,262,112,162,126,815,088,519,757,781,226,609,803,442,241,929,696,393
,506,490,927,126,295,938,550,250,225,742,914,776,562,115,220,551,324,548,606,709,523,751,866,622,058
,233,545,014,546,787,540,934,003,075,335,883,885,669,363,860,915,505,255,437,739,250,276,667,735,923
,338,774,660,174,357,055,927,249,298,888,125,358,649,886,990,161,392,255,374,135,288,975,587,508,386
,599,278,357,138,736,974,752,376,121,439,454,468,521,560,742,737,593,871,963,162,251,707,271,516,614
,404,464,184,535,686,394,022,712,531,998,647,041,816,974,083,067,995,107,365,568,144,175,444,000,768

which is somewhere around 7.824 x 10^(-10)

Wizard
Administrator

Threads: 1517
Posts: 27009

Joined: Oct 14, 2009

October 10th, 2020 at 9:04:45 AM permalink

Quote: Ace2
Chesterdog and Wizard, that is the correct exact answer.

Use Sterling's formula (n/e)^n * (2πn)^.5 for very accurate estimates of the factorials.

When you substitute it into the exact formula 6000!/((1000!)^6 * 6^6000), terms cancel nicely to get:

6^.5 / (2π1000)^2.5 = 7.8276 * 10^-10

Within 0.05% of the exact answer

Thanks. I hadn't seen Sterling's formula in a long time and forgot about it.

However, this doesn't seem to help if we're limited to ordinary calculators.

For example, let's try to get an estimate of 6000! Sterling says that is sqrt(2 * pi * 6000)*(6000/e)^6000.

Excel conks out at (6000/e)^6000.

However, lets try to find ln(6000!). That would be ln(2*pi*6000) + 6000*ln(6000/e).

= 10.5374 + 46,197 = 46,207.

Exp(46,207) causes Excel to conk out.

ln(6000!) = 46202.357199, so I agree Sterling does provide a very good estimate.

Maybe it wasn't the question being asked, so I'll ask it. How can one get a good numerical estimate for the question at hand using just Excel?

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

Ace2

Ace2

Threads: 32
Posts: 2706

Joined: Oct 2, 2017

Thanked by

October 10th, 2020 at 9:49:50 AM permalink

Quote: Wizard
Thanks. I hadn't seen Sterling's formula in a long time and forgot about it.

However, this doesn't seem to help if we're limited to ordinary calculators.

For example, let's try to get an estimate of 6000! Sterling says that is sqrt(2 * pi * 6000)*(6000/e)^6000.

Excel conks out at (6000/e)^6000.

However, lets try to find ln(6000!). That would be ln(2*pi*6000) + 6000*ln(6000/e).

= 10.5374 + 46,197 = 46,207.

Exp(46,207) causes Excel to conk out.

ln(6000!) = 46202.357199, so I agree Sterling does provide a very good estimate.

Maybe it wasn't the question being asked, so I'll ask it. How can one get a good numerical estimate for the question at hand using just Excel?

You don�t need excel or even a calculator for this

(6000/e)^6000 * (2π6000)^.5 / (((1000/e)^1000 * (2π1000)^.5)^6* 6^6000) =

6^.5 / (2π1000)^2.5 = 7.83 * 10^-10

Which you can do with a pen, paper and maybe a slide rule to get three significant digits. E and the huge numbers in the first formula cancel out before you need to calculate anything, which is the beauty of it...

Last edited by: Ace2 on Oct 10, 2020

It�s all about making that GTA

Gialmere

Threads: 45
Posts: 3044

Joined: Nov 26, 2018

October 10th, 2020 at 1:09:08 PM permalink

You have a deck of 28 cards: 8 through ace in four suits.

Arrange 25 of these cards in the five-by-five grid so that the 12 named poker hands appear in the rows, columns and diagonals.

The location of some cards and suits are given.

Have you tried 22 tonight? I said 22.

charliepatrick

Threads: 39
Posts: 3011

Joined: Jun 17, 2011

Thanked by

October 10th, 2020 at 3:31:31 PM permalink

Lovely problem, logic needed to work through it - hopefully I've not missed anything.

					Pair
A♣	8♦	8♠	A♠	10♠	Two Pairs
9♠	Q♣	Q♦	A♦	10♦	Pair
K♥	K♦	K♣	J♥	K♠	Quads
9♥	8♥	Q♥	J♣	10♥	Straight
A♥	8♣	J♦	J♠	10♣	Pair
2P	3	Pair	FH	Qu	R Flush

Gialmere

Threads: 45
Posts: 3044

Joined: Nov 26, 2018

October 11th, 2020 at 12:12:43 PM permalink

Quote: charliepatrick
Lovely problem, logic needed to work through it - hopefully I've not missed anything.
Pair
A♣ 8♦ 8♠ A♠ 10♠ Two Pairs
9♠ Q♣ Q♦ A♦ 10♦ Pair
K♥ K♦ K♣ J♥ K♠ Quads
9♥ 8♥ Q♥ J♣ 10♥ Straight
A♥ 8♣ J♦ J♠ 10♣ Pair
2P 3 Pair FH Qu R Flush

Correct!

-----------------------------------

I won my poker tournament last night with the five of clubs and the five of spades.

Black fives matter.

Have you tried 22 tonight? I said 22.

Wizard
Administrator

Threads: 1517
Posts: 27009

Joined: Oct 14, 2009

October 11th, 2020 at 7:38:43 PM permalink

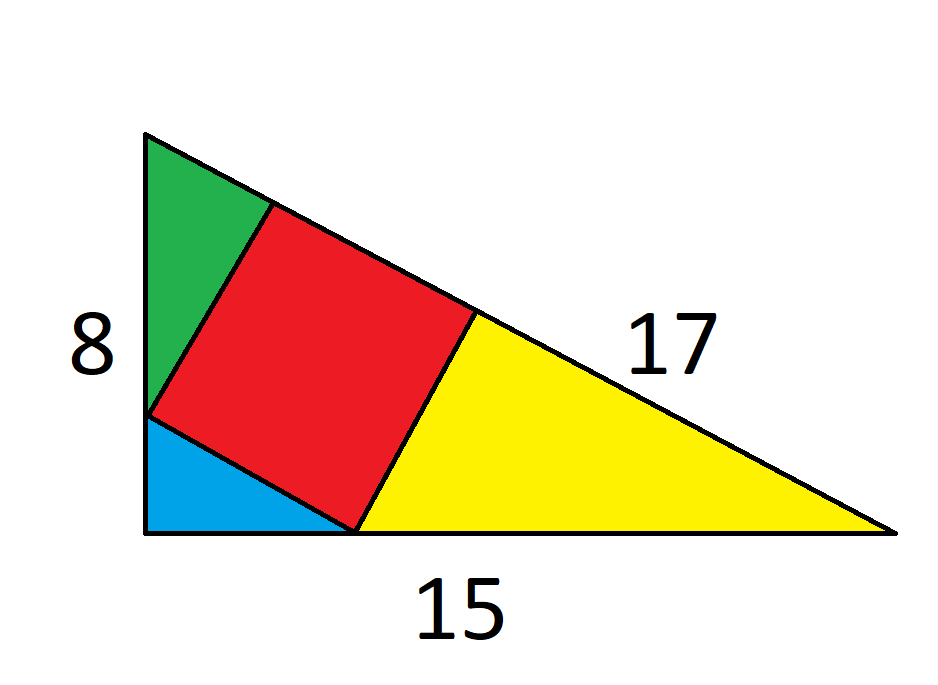
A red square is inscribed in an 8-15-17 right triangle. What is the length of the side of the square?

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

ChesterDog

Threads: 9
Posts: 1702

Joined: Jul 26, 2010

October 11th, 2020 at 8:28:21 PM permalink

Quote: Wizard

A red square is inscribed in an 8-15-17 right triangle. What is the length of the side of the square?

The four triangles are all similar right triangles.

Call the square�s side a.

The blue triangle�s height is 8a/17.

The green triangle�s hypotenuse is 17a/15.

The height of the big triangle, 8, is equal to the sum of the blue triangle�s height and the green triangle�s hypotenuse, 8a/17 + 17a/15.

8a/17 + 17a/15 = 8

Multiplying by sides by (15)(17) yields:

(8)(15)a + 17²a = (8)(15)(17)

So:
a = (8)(15)(17) / [ (8)(15) + 17² ], which is about 4.99.

Wizard
Administrator

Threads: 1517
Posts: 27009

Joined: Oct 14, 2009

October 11th, 2020 at 8:50:41 PM permalink

Quote: ChesterDog

The four triangles are all similar right triangles.

Call the square�s side a.

The blue triangle�s height is 8a/17.

The green triangle�s hypotenuse is 17a/15.

The height of the big triangle, 8, is equal to the sum of the blue triangle�s height and the green triangle�s hypotenuse, 8a/17 + 17a/15.

8a/17 + 17a/15 = 8

Multiplying by sides by (15)(17) yields:

(8)(15)a + 17²a = (8)(15)(17)

So:
a = (8)(15)(17) / [ (8)(15) + 17² ], which is about 4.99.

I agree!

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

gordonm888
Administrator

gordonm888

Threads: 61
Posts: 5347

Joined: Feb 18, 2015

Thanked by

October 12th, 2020 at 10:37:17 AM permalink

Quote: charliepatrick
Lovely problem, logic needed to work through it - hopefully I've not missed anything.
Pair
A♣ 8♦ 8♠ A♠ 10♠ Two Pairs
9♠ Q♣ Q♦ A♦ 10♦ Pair
K♥ K♦ K♣ J♥ K♠ Quads
9♥ 8♥ Q♥ J♣ 10♥ Straight
A♥ 8♣ J♦ J♠ 10♣ Pair
2P 3 Pair FH Qu R Flush

I also got the same answer as Charlie - and I agree, it was a very well-designed and fun puzzle. Lots of different kinds of constraints and starting conditions for various squares.

So many better men, a few of them friends, are dead. And a thousand thousand slimy things live on, and so do I.

Wizard
Administrator

Threads: 1517
Posts: 27009

Joined: Oct 14, 2009

October 12th, 2020 at 11:09:16 AM permalink

I agree, a fun problem. My first attempted to solve it looked it would be a very difficult, with seven equations and seven unknowns.

However, once you realize all four triangles are similar, the rest is easy.

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

Gialmere

Threads: 45
Posts: 3044

Joined: Nov 26, 2018

October 12th, 2020 at 1:55:20 PM permalink

Here's an easy Monday puzzle...

MrCasinoGames has designed a most unusual roulette wheel having eighteen numbers around the rim and a single number in the middle. He arranged the numbers so that any three lying on a line through the middle will add up to exactly the same amount.

Can you fill them in?

[Note that the wheel contains no zero.]

Have you tried 22 tonight? I said 22.

gordonm888
Administrator

gordonm888

Threads: 61
Posts: 5347

Joined: Feb 18, 2015

Thanked by

October 12th, 2020 at 2:31:30 PM permalink

Quote: Gialmere
Here's an easy Monday puzzle...

MrCasinoGames has designed a most unusual roulette wheel having eighteen numbers around the rim and a single number in the middle. He arranged the numbers so that any three lying on a line through the middle will add up to exactly the same amount.

Can you fill them in?

[Note that the wheel contains no zero.]

Good lord, this is an easy puzzle!

If the 19 numbers are 1-19, place the ten in the middle position and have opposing numbers add up to 20.

So many better men, a few of them friends, are dead. And a thousand thousand slimy things live on, and so do I.

Gialmere