Poll
 | 21 votes (45.65%) | ||
 | 14 votes (30.43%) | ||
 | 6 votes (13.04%) | ||
 | 3 votes (6.52%) | ||
 | 12 votes (26.08%) | ||
 | 3 votes (6.52%) | ||
 | 6 votes (13.04%) | ||
 | 5 votes (10.86%) | ||
 | 12 votes (26.08%) | ||
 | 10 votes (21.73%) |
46 members have voted
June 16th, 2025 at 11:15:17 AM
permalink
Quote: ThatDonGuy
To 100 places, I get:
0.14015 01597 77671 70675 03301 99764 58363 24852 96210 37282 37474 09380 11959 51720 40943 79197 71682 53488 94282 64038
link to original post
I agree.
June 26th, 2025 at 6:48:47 PM
permalink
I've done a quick spreadsheet which looks at all the permutaions of 6-13 (i.e. 8*8*8*8) and assumes there are only 4 of each rank. However a trick I've used (see 6 6 7 6 where there's a tie) is to divide the 96 ways to get it, so each of the winners have 48 wins each. This is why the total includes 2/3 as there can be 3-way ties.
I haven't checked anything but it shouldn't take long to knock up a similar spreadsheet.
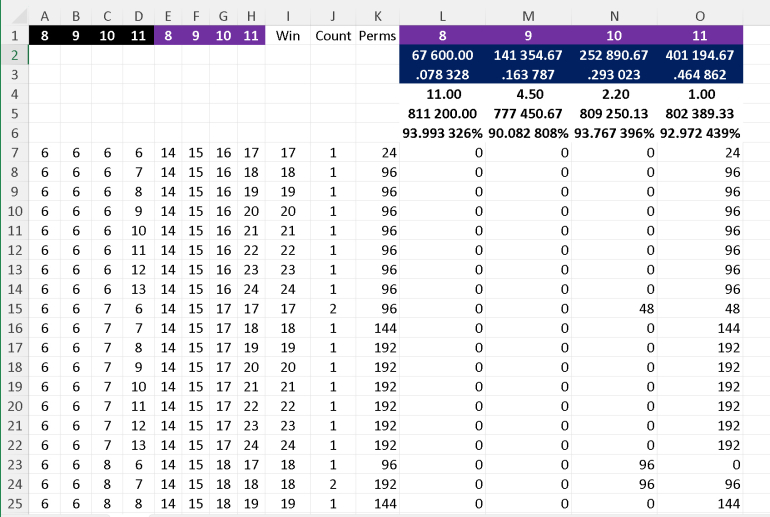
I haven't checked anything but it shouldn't take long to knock up a similar spreadsheet.

June 26th, 2025 at 8:43:55 PM
permalink
Quote: charliepatrickI've done a quick spreadsheet
link to original post
We're pretty close, but not quite in agreement. Probably something to do with the ties. My figures are the page I linked to.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
June 27th, 2025 at 4:52:23 AM
permalink
I'm pretty sure the error is on my end, but I can't find it.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
June 27th, 2025 at 5:56:58 AM
permalink
I found it. Stupid mistake, as usual. I definitely owe you a beer for this one.
Updated table.
Updated table.
| Winner | Pays | Probability | Return |
|---|---|---|---|
| 8 | 11 | 0.078328 | -0.060067 |
| 9 | 4.5 | 0.163787 | -0.099172 |
| 10 | 2.2 | 0.293023 | -0.062326 |
| 11 | 1 | 0.464862 | -0.070276 |
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
June 28th, 2025 at 4:39:24 PM
permalink
No mention of ties? e. g., deck composition KQKQKKQQJJJJTTTT9999888877776666. I think there might be over two trillion deck permutations resulting in a tie. I was working on a finite proof with Python programming that was easy peasy for the initial deal, but bogged down as I worked to resolve ties. On reasoning how far must be gone and how often, I see why my laptop does not have the horsepower for that type of solution. (Edit: revised estimate from one to two trillion.)
“You don’t bring a bone saw to a negotiation.” - Robert Jordan, former U.S. ambassador to Saudi Arabia
June 29th, 2025 at 2:45:51 AM
permalink
Quote: BleedingChipsSlowlyNo mention of ties?
link to original post
Once the game gets to a tie, it becomes a coin flip.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
June 29th, 2025 at 3:17:18 AM
permalink
The number of different orders of 32 cards ignoring the suits is 32!/(4!)8, about 2.4*1024. Even if a few trillion of them result in a tie, the probability is tiny.
June 30th, 2025 at 11:06:28 AM
permalink
Here are some belated Easy Monday puzzles...

The U.S. debt is measured in trillions of dollars.
Could a New York Times reporter have written about this story one trillion seconds ago?

As seen from the surface of earth, the sun and the moon appear to be the same size. The sun is actually 400 times larger than the moon.
How far away from earth is the sun compared to how far away the moon is?
%2Fpic148345.jpg&f=1&ipt=c26ce95d0258ba6b7cadd6064529d544cc40f79af89e03c90b11d0cf575dcf24)
The board game Magic Realm has an unusual dice mechanic. Two standard six-sided dice are rolled, but only the higher of the two numbers acts as the result.
For example:
A 1-6 would = 6
A 3-4 would = 4
A 2-2 would = 2
What is the probability of getting a result of 5?

The U.S. debt is measured in trillions of dollars.
Could a New York Times reporter have written about this story one trillion seconds ago?
As seen from the surface of earth, the sun and the moon appear to be the same size. The sun is actually 400 times larger than the moon.
How far away from earth is the sun compared to how far away the moon is?
%2Fpic148345.jpg&f=1&ipt=c26ce95d0258ba6b7cadd6064529d544cc40f79af89e03c90b11d0cf575dcf24)
The board game Magic Realm has an unusual dice mechanic. Two standard six-sided dice are rolled, but only the higher of the two numbers acts as the result.
For example:
A 1-6 would = 6
A 3-4 would = 4
A 2-2 would = 2
What is the probability of getting a result of 5?
Have you tried 22 tonight? I said 22.
June 30th, 2025 at 11:19:15 AM
permalink
1. No. That comes to 31,710 years. I doubt there was a concept or term for numbers that big back then. Interesting thought.
2. If "size" is measured as volume, then I get 40^(1/3) =~ 7.368 times as far away.
3. 9/36 = 1/4.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
June 30th, 2025 at 11:51:30 AM
permalink
Quote: Wizard
1. No. That comes to 31,710 years. I doubt there was a concept or term for numbers that big back then. Interesting thought.
2. If "size" is measured as volume, then I get 40^(1/3) =~ 7.368 times as far away.
3. 9/36 = 1/4.
link to original post
2. Not volume but diameter. (Think solar eclipse.)
It's very easy Monday.
Have you tried 22 tonight? I said 22.
June 30th, 2025 at 3:38:57 PM
permalink
Quote: GialmereHere are some belated Easy Monday puzzles...
link to original post
Time: there are 86,400 < 100,000 seconds per day, and 365.25 or so < 400 days per year, so there are < 40 million seconds per year, which means there are < 40 million x 25,000, or < 1 trillion, seconds in 25,000 years. Since the NYT was not around 25,000 years ago, it could not have reported on anything 1 trillion seconds ago.
Space: assuming the diameter of the sun is 400 times the diameter of the moon, it must be 400 times as far from Earth as the moon in order for the two to appear to be the same size. Think of the diameter of each as the far end of an isosceles triangle; you have two similar triangles.
Dice: of the 36 possible rolls of 2 dice, 11 of them (1-5 through 4-5, and 5-1 through 5-5) have the highest number 5, so the probability is 11/36.
Side note: you would think that, given how many games printed by the old Avalon Hill Game Company have been reprinted by other companies since its demise around 25 years ago, this one would have been reprinted at least once, but it has not.
June 30th, 2025 at 7:16:31 PM
permalink
Quote: Wizard
1. No. That comes to 31,710 years. I doubt there was a concept or term for numbers that big back then. Interesting thought.
2. If "size" is measured as volume, then I get 40^(1/3) =~ 7.368 times as far away.
3. 9/36 = 1/4.
link to original post
Quote: ThatDonGuy
Time: there are 86,400 < 100,000 seconds per day, and 365.25 or so < 400 days per year, so there are < 40 million seconds per year, which means there are < 40 million x 25,000, or < 1 trillion, seconds in 25,000 years. Since the NYT was not around 25,000 years ago, it could not have reported on anything 1 trillion seconds ago.
Space: assuming the diameter of the sun is 400 times the diameter of the moon, it must be 400 times as far from Earth as the moon in order for the two to appear to be the same size. Think of the diameter of each as the far end of an isosceles triangle; you have two similar triangles.
Dice: of the 36 possible rolls of 2 dice, 11 of them (1-5 through 4-5, and 5-1 through 5-5) have the highest number 5, so the probability is 11/36.
Side note: you would think that, given how many games printed by the old Avalon Hill Game Company have been reprinted by other companies since its demise around 25 years ago, this one would have been reprinted at least once, but it has not.
link to original post
Correct!
Good show.
One billion seconds ago would take us back to the 1990's where a Times reporter could easily write about the U.S. debt. One trillion seconds ago, however, would find us in an age when the invention of writing itself was many, many thousand of years in the future and never mind the founding of the Gray Lady.
While the sun is 400 times the size of the moon, it is also 400 times further away from earth. So both objects appear to us to be the same size.
Note that the moon is moving away from the earth at a rate of around 1.5 inches per year. Thus, on some future date, complete solar eclipses will no longer occur as the moon will be too far away to entirely block off the sun. On the other hand, a few billion years ago the moon would have appeared to be much larger than the sun, solar eclipses would have been wider ranging and also longer lasting.
Note that the moon is moving away from the earth at a rate of around 1.5 inches per year. Thus, on some future date, complete solar eclipses will no longer occur as the moon will be too far away to entirely block off the sun. On the other hand, a few billion years ago the moon would have appeared to be much larger than the sun, solar eclipses would have been wider ranging and also longer lasting.
You have a 25% chance of rolling a 5. As you might imagine, the lower the result, the better for the player
Also, as mentioned, the game is no longer in print. Old copies in good condition can fetch $400 to $500 dollars at ebay.
Also, as mentioned, the game is no longer in print. Old copies in good condition can fetch $400 to $500 dollars at ebay.
----------------------------------------
...but he couldn't get a straight answer from anyone.
Have you tried 22 tonight? I said 22.
July 8th, 2025 at 9:44:22 AM
permalink
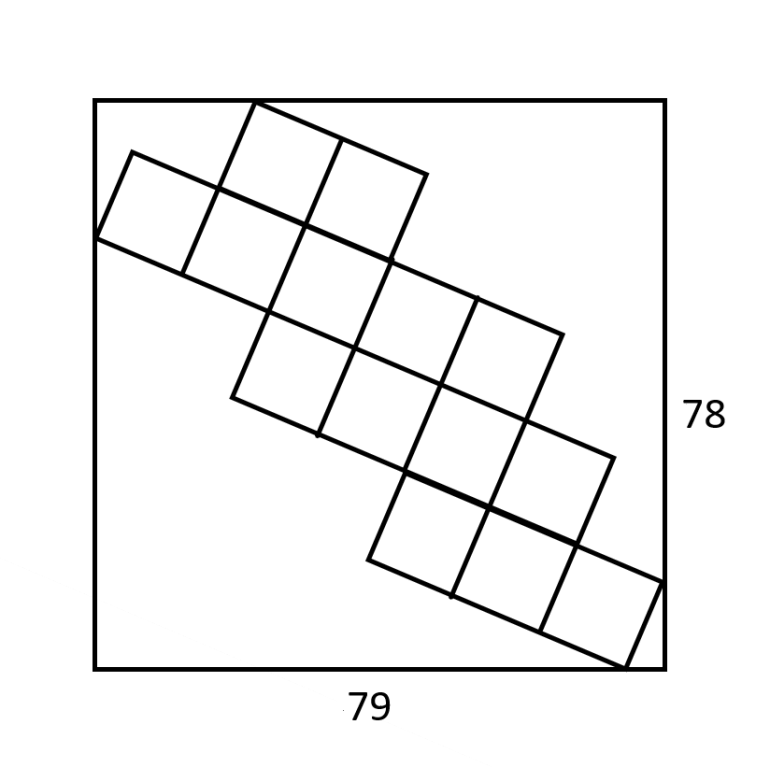
Update (4:15 PM 7/8/25): Horizontal length changed to 65.
Update (10:50 AM 7/9/25): Horizontal length changed to 79, vertical to 80.
Update (8:10 PM 7/9/25): Vertical length changed to 78.
The big rectangle has the dimensions indicated in the image above. The squares inside it are all equal in size. What is the length of the side of each square?
Fair warning that I found this one harder than it looks. Beer for the first correct solution.
Last edited by: Wizard on Jul 9, 2025
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
July 9th, 2025 at 6:12:39 AM
permalink
Quote: Wizard
Update (4:15 PM 7/8/25): Horizontal length changed to 65.
The big rectangle has the dimensions indicated in the image above. The squares inside it are all equal in size. What is the length of the side of each square?
Fair warning that I found this one harder than it looks. Beer for the first correct solution.
link to original post
Using vector math, I get 13/23 times the square root of 445.
(If my answer is right, I'll show the work.)
July 9th, 2025 at 6:27:33 AM
permalink
Quote: ChesterDog
Using vector math, I get 13/23 times the square root of 445.
(If my answer is right, I'll show the work.)
link to original post
Maybe I'm the one in error, but I get something else. Did you note the changed width to 65?
Third opinion anyone?
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
July 9th, 2025 at 6:35:36 AM
permalink
Quote: WizardQuote: ChesterDog
Using vector math, I get 13/23 times the square root of 445.
(If my answer is right, I'll show the work.)
link to original post
Maybe I'm the one in error, but I get something else. Did you note the changed width to 65?
Third opinion anyone?
link to original post
I am still working on it
July 9th, 2025 at 10:52:06 AM
permalink
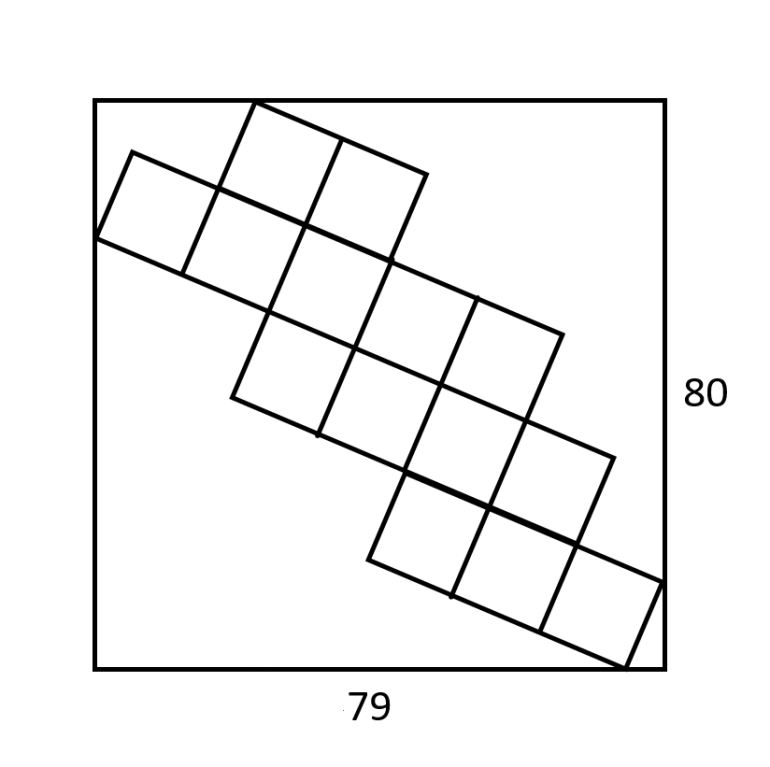
I apologize, but I found an error in my work. To make the math easier, I changed changed the dimensions again to 79 horizontal to 80 vertical. I apologize for the change. I do not think this is the only reason for my disagreement with CD.

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
July 9th, 2025 at 1:36:54 PM
permalink
7.95 ? i can show work, but no idea if this is correct
July 9th, 2025 at 2:21:11 PM
permalink
Add triangles with small size x and large y. The aim is to find SQRT(x^2+y^2).
See diagram then solve the simultaneous equations, by adding up how many sides of triangles make the height and width.
80=6x+4y. 79=7y-x.
474=42y-6x. 554=46y.
y=277/23 x=122/23
Hence x^2+y^2 = (76729+14884)/(23*23) = 91613/(23*23).
Hence side of square is SQRT(91613)/23 which is about 13.1598.
It would have been nice if this had landed up as a whole number!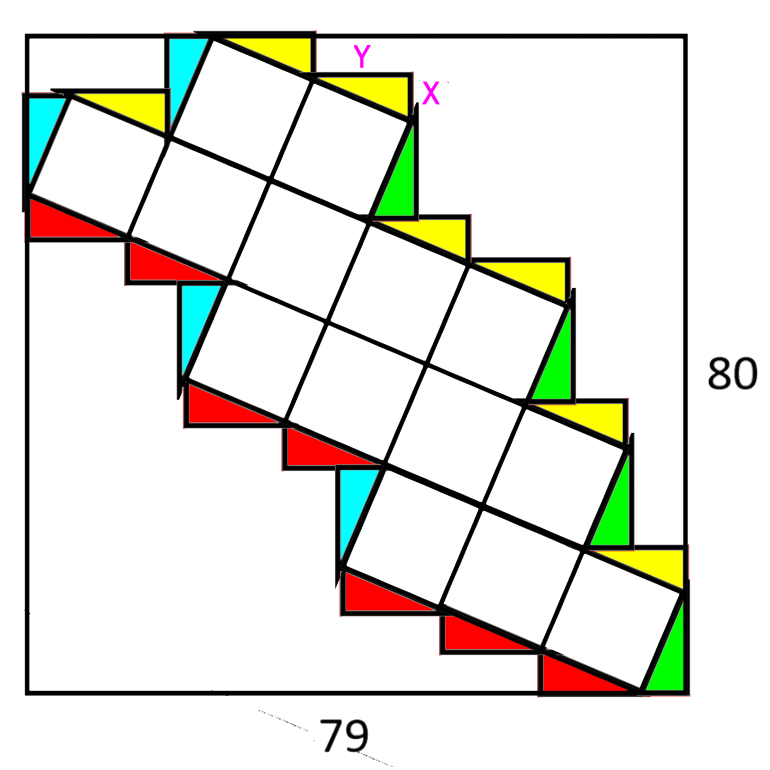
See diagram then solve the simultaneous equations, by adding up how many sides of triangles make the height and width.
80=6x+4y. 79=7y-x.
474=42y-6x. 554=46y.
y=277/23 x=122/23
Hence x^2+y^2 = (76729+14884)/(23*23) = 91613/(23*23).
Hence side of square is SQRT(91613)/23 which is about 13.1598.
It would have been nice if this had landed up as a whole number!

July 9th, 2025 at 2:30:20 PM
permalink
Using above logic you get 78=6x+4y and 79=7y-x. This gives x=5 y=12... and we recognise it as a 5 12 13 triangle. Nice whole numbers!!
July 9th, 2025 at 8:12:38 PM
permalink
Charlie is absolutely right. My vertical length should have been 78 to make the answer a round number.
My apologies for three corrections.
Charlie earns more than a beer for this one.
My apologies for three corrections.
Charlie earns more than a beer for this one.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
July 10th, 2025 at 7:11:42 AM
permalink
Ah yes, a nice perfect Pythagorean triple, beautiful math, I can see what you were going for now.
July 10th, 2025 at 7:42:49 AM
permalink
The trace of a square matrix is the sum of the entries on the main diagonal.
1. Show that the trace of AB is the trace of BA where A and B are square matrices of the same size.
2. Prove that similar matrices have the same trace.
3. Develop a definition of the trace of a linear transformation T : V → V of a finite dimensional vector
space. Explain why it is well defined?
4. Describe the trace in terms of the characteristic polynomial of T and also in terms of the eigenvalues.
1. Show that the trace of AB is the trace of BA where A and B are square matrices of the same size.
2. Prove that similar matrices have the same trace.
3. Develop a definition of the trace of a linear transformation T : V → V of a finite dimensional vector
space. Explain why it is well defined?
4. Describe the trace in terms of the characteristic polynomial of T and also in terms of the eigenvalues.
July 14th, 2025 at 2:19:21 PM
permalink
Sorry to step on the problem above this one. To be honest, I think that one is above my level, unless it can be put into more plain simple English.
For this question, consider any Crash game.
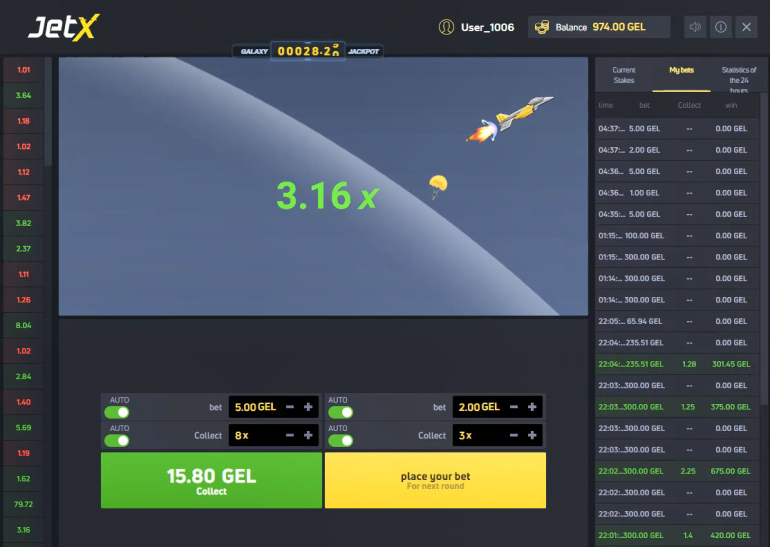
Briefly, this is a game where the player can cash out at any time. If he doesn't, his win grows exponentially. However, he can "crash" at anytime and lose.
For the same of this analysis, assume it is a fair bet whether to play on or not.
My questions are what are the mean and median levels the rocket will attain. Be careful to not solve for the time until crash, but the balance at the time of the crash.
For this question, consider any Crash game.

Briefly, this is a game where the player can cash out at any time. If he doesn't, his win grows exponentially. However, he can "crash" at anytime and lose.
For the same of this analysis, assume it is a fair bet whether to play on or not.
My questions are what are the mean and median levels the rocket will attain. Be careful to not solve for the time until crash, but the balance at the time of the crash.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
July 14th, 2025 at 3:48:14 PM
permalink
Assume, for simplicity, that it's a discrete game where every minute you either crash or the value goes up. You get a chance to cash out or wait for the next decision.
Let say the chances of losing at the end of the current minute is 1/N. Then the fair price after the first minute is N/(N-1). The chances the rocket fails with the price at 1 is 1/N, so the contribution to the mean is 1/N.
After the second minute the fair price is now N2/((N-1)2) and the chances the rocket fails with the price at N/(N-1) is (N-1)/N*1/N; so the contribution to the mean is also 1/N.
Thus I think the mean is infinite and seems similar to tossing coins where the value doubles on a Head or loses on a Tail. There's a 1/4 chance of getting to 2 and losing (HT), there's a 1/8 chance of getting to 4 and losing (HHT)... etc. Each of these add 1/2 to the average, so the mean is infinite.
I suspect the median can be based on a poisson formula, and will depend on the chances the rocket crashes in any given time. For instance if the chance of losing each minute is 1/1000 it's about 693 minutes, when the price has got the 2. So you could work out x such that ((n+1)/n)x=2.
Let say the chances of losing at the end of the current minute is 1/N. Then the fair price after the first minute is N/(N-1). The chances the rocket fails with the price at 1 is 1/N, so the contribution to the mean is 1/N.
After the second minute the fair price is now N2/((N-1)2) and the chances the rocket fails with the price at N/(N-1) is (N-1)/N*1/N; so the contribution to the mean is also 1/N.
Thus I think the mean is infinite and seems similar to tossing coins where the value doubles on a Head or loses on a Tail. There's a 1/4 chance of getting to 2 and losing (HT), there's a 1/8 chance of getting to 4 and losing (HHT)... etc. Each of these add 1/2 to the average, so the mean is infinite.
I suspect the median can be based on a poisson formula, and will depend on the chances the rocket crashes in any given time. For instance if the chance of losing each minute is 1/1000 it's about 693 minutes, when the price has got the 2. So you could work out x such that ((n+1)/n)x=2.
July 14th, 2025 at 4:53:48 PM
permalink
In this case, since it is a fair game, the game consists of selecting a uniform random number x in (0,1] and the crash value is 1/x.
Since x is uniform, the median value is where x = 1/2, so it is 2.
The mean is the area underneath the graph divided by the length of the domain; since the domain has length 1, it is INTEGRAL(0, 1) (1/x dx) = ln 1 - ln 0, which is positive infinity. Somehow, that doesn't make sense...