Poll
 | 25 votes (49.01%) | ||
 | 16 votes (31.37%) | ||
 | 7 votes (13.72%) | ||
 | 4 votes (7.84%) | ||
 | 12 votes (23.52%) | ||
 | 3 votes (5.88%) | ||
 | 6 votes (11.76%) | ||
 | 5 votes (9.8%) | ||
 | 12 votes (23.52%) | ||
 | 10 votes (19.6%) |
51 members have voted
Quote: ThatDonGuy
Label the rows A-E from top to bottom, and the columns 1-5 from left to right
Numbers in curly braces can be in any order
B1-D1 is {1 2 4}
C3-C5 is {3 4 5}
D4-D5 is {1 3}
E1-E3 is {2 4 5}
A1-A3 is {1 3 5} or {2 3 4}
A5-B5 is {1 4} or {2 3}
C2-D3 is {1 4 1} or {1 2 3}
D5-E5 is {1 5} or {2 4}
If A5-B5 is {4 1}, D5-E5 cannot be any valid pair
Therefore A5-B5 is {2 3} and D5-E5 is {1 5}, which means C5 = 4,
which mens C2-D3 cannot be {1 4 1}, so it must be {1 2 3}
C2 cannot be 3, so either D2 or D3 = 3, which means D4 cannot be 3,
which means D4 = 1 and D5 = 3
Since E1-E4 have 2, 3, 4, and 5 in them, E5 = 1, which means D5 = 5
Since D4 = 1, D2 and D3 cannot be 1, so C2 = 1
Since C2-C5 have 1, 3, 4, and 5 in them, C3 = 2
C4 cannot be 1, 2, 3, or 4, so it is 5, and C3 = 3
This means that A4-B4 are {2 4}, so B3 = 5
Also, since B2 = 4, B4 cannot be 4, so it is 2, and A4 = 4
B2 cannot be 1, 4, 5, or 2, so it is 3, and A5 = 2; also, B1 = 1, so D1 = 4
D3 cannot be 4, 1, 5, or 3, so it is 2, and D2 = 3
E3 cannot be 5, 3, 2, or 1, so it is 4, and A3 = 1
A2 cannot be 4, 1, 3, or 2, so it is 5, and A1 = 3, which means E1 = 5 and E2 = 2
Each row, from left to right:
3 5 1 4 2
1 4 5 2 3
2 1 3 5 4
4 3 2 1 5
5 2 4 3 1
The solution is unique
Correct!
-------------------------------

It starts with a bin of 35 balls numbered 1-35. You pick one number and you win $100 if itís drawn. Only one ball is ever drawn from the bin
Then there is a second drawing for which 2 x 32 balls are added to the bin. You pick a number 1-99 and win $100 if itís drawn
Then there is a third drawing for which 3 x 32 balls are added to the bin. You pick a number 1-195 and win $100 if itís drawn
And so on.
The drawings and ball additions continue for as long as you want to play. You get paid $100 for every win...no limit
If this game was priced fairly, how much would it cost to play it ?
Quote: rsactuary[\spoiler]
That should be [/spoiler]
Speaking of which...
The expected return is is the sum over all positive integers n of 100 / ((4n + 2)^2 - 1).
I have a feeling this is a little above my math pay grade. I am still trying to figure out how the sum of the reciprocals of the squares is PI^2 / 6.
Quote: Ace2Thereís a new casino game that plays as follows.
It starts with a bin of 35 balls numbered 1-35. You pick one number and you win $100 if itís drawn. Only one ball is ever drawn from the bin
Then there is a second drawing for which 2 x 32 balls are added to the bin. You pick a number 1-99 and win $100 if itís drawn
Then there is a third drawing for which 3 x 32 balls are added to the bin. You pick a number 1-195 and win $100 if itís drawn
And so on.
The drawings and ball additions continue for as long as you want to play. You get paid $100 for every win...no limit
If this game was priced fairly, how much would it cost to play it ?
That is the correct answer. However, ďfor full creditĒ Iíd like to see an explanation why itís the answer.Quote: unJonThis looks like itís the sum from N=1 to infinity of 100/(3+32N(N+1)/2). Wolfram alpha says that sums to 25/6(3pi -8). Or about $5.93654.
Quote: Ace2That is the correct answer. However, ďfor full creditĒ Iíd like to see an explanation why itís the answer.
As soon as I figure out how the sum over all positive integers n of 1 / ((4n + 2)^2 - 1) = (1 - 1/3 + 1/5 - 1/7 + ...) / 2 - 1/3, I'll let you know.

An advertisement on TV for an injury law firm states...
"What can happen in 5 seconds? A driver can send a text message and drive blindly down the road for 300 feet. If you have been injured in those 5 seconds, call us at ..."
How fast would the driver mentioned in this TV ad have been going (in mph to the nearest tenth)?
Quote: Ace260^2 / 5 * 300 / 5,280 =~40.9 mph
Correct!
--------------------------------

He says to the doctor "Oh god I can't feel my legs"
The doctor says "I know, I amputated your arms."
Youíre on the right track.Quote: ThatDonGuyAs soon as I figure out how the sum over all positive integers n of 1 / ((4n + 2)^2 - 1) = (1 - 1/3 + 1/5 - 1/7 + ...) / 2 - 1/3, I'll let you know.
π/4 = 1 - 1/3 + 1/5 - 1/7 ....
If you combine the terms in pairs, eliminating the negatives, you get 2/3 + 2/35 + 2/99 + 2/195...Then subtract the 2/3, then multiply by 50 to get:
100(1/35 + 1/99 + 1/195...) =
50(π/4 - 2/3) =~ $5.94
Quote: Ace2Youíre on the right track.
π/4 = 1 - 1/3 + 1/5 - 1/7 ....
If you combine the terms in pairs, eliminating the negatives, you get 2/3 + 2/35 + 2/99 + 2/195...Then subtract the 2/3, then multiply by 50 to get:
100(1/35 + 1/99 + 1/195...) =
50(π/4 - 2/3) =~ $5.94
Got it.
The number of balls in the nth draw = 32 (1 + 2 + ... + n) + 3 = 32 n (n + 1) / 2 + 3 = 16 n^2 + 16 n + 3 = (4n + 2)^2 - 1
The probability of winning in the nth draw = 1 / (4n + 2)^2 - 1
The expected return is 100 x the sum of (1 / (4n + 2)^2 - 1) over all positive integers n
= 100 (1 / ((4n + 2)^2 - 1))
= 100 (1 / (6^2 - 1) + 1 / (10^2 - 1) + 1 / (14^2 - 1) + ...)
= 100 ((1/3 + 1 / (6^2 - 1) + 1 / (10^2 - 1) + 1 / (14^2 - 1) + ...) - 1/3)
= 100 ((2/3 + 2 / (6^2 - 1) + 2 / (10^2 - 1) + 2 / (14^2 - 1) + ...) / 2 - 1/3)
= 100 ((2/3 + 2 / (5 x 7) + 2 / (9 x 11) + 2 / (13 x 15) + ...) / 2 - 1/3)
= 100 (((1 - 1/3) + (1/5 - 1/7) + (1/9 - 1/11) + (1/13 - 1/15) + ...) / 2 - 1/3)
= 100 (PI/8 - 1/3)
= 25 PI / 2 - 100 / 3 = about 5.94
Wizard, if I still have any beers on my tab, you can give one to Ace2 - I learned at the last Spring Fling I went to that I just can't taste beers very well (they all taste like alcohol).
Quote: ThatDonGuy
Wizard, if I still have any beers on my tab, you can give one to Ace2 - I learned at the last Spring Fling I went to that I just can't taste beers very well (they all taste like alcohol).
I'd be happy to enjoy a beer with either of you. Also, substitutions may be made for drinks of equal or lesser value ;-).
It will be fun talking about e, pi and Poisson. All women within a mile of the bar will evacuateQuote: WizardI'd be happy to enjoy a beer with either of you. Also, substitutions may be made for drinks of equal or lesser value ;-).
Quote: Ace2All women within a mile of the bar will evacuate
I am used to that. I like to say that I have a certain magnetism when it comes to the ladies. Unfortunately, it is the repelling kind.
Quote: WizardI am used to that. I like to say that I have a certain magnetism when it comes to the ladies. Unfortunately, it is the repelling kind.
I would think your beard should help.
Especially, if you weave it into a net.
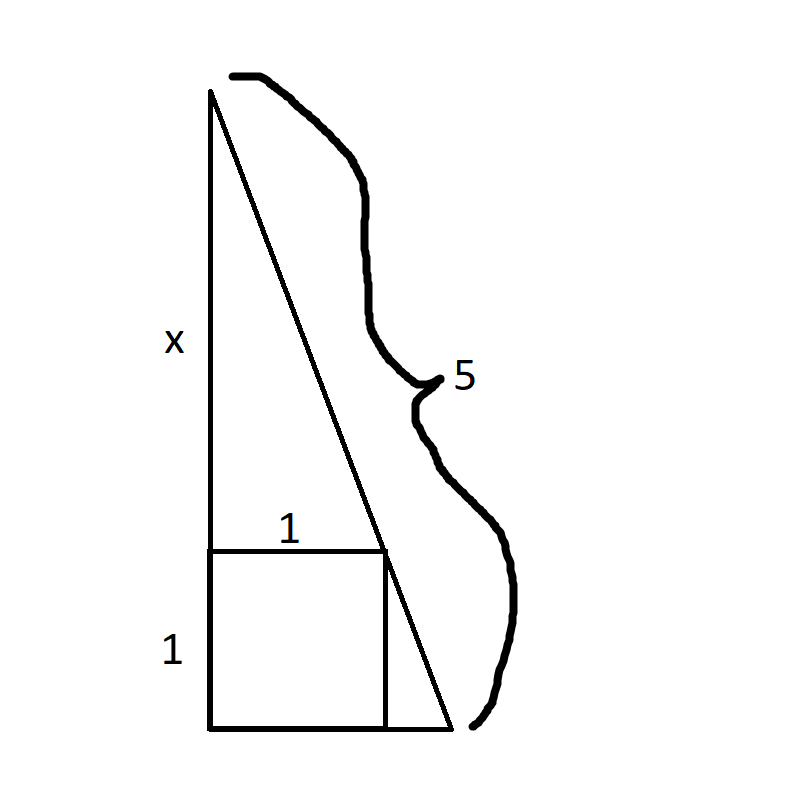
In a two-dimensional world, A 5' ladder rests against the wall in an alley as well as touches the corner of a 1'x1' box, in which both one corner of the box fits into the corner of the ground and wall in the alley.
Find x.
In all fairness, a decimal representation to six decimal points is all that I ask.
Quote: WizardIn a two-dimensional world, A 5' ladder rests against the wall in an alley as well as touches the corner of a 1'x1' box, in which both one corner of the box fits into the corner of the ground and wall in the alley.
Find x.
In all fairness, a decimal representation to six decimal points is all that I ask.
Label the vertices of the triangle A, B, C such that AB is the hypotenuse and AC is the vertical (i.e. AC has length X + 1).
Label the remaining vertices of the square D, E, F such that CDEF is the square (i.e. D is on AC, E is on AB, abd F is on BC).
ADE is similar to EFB, so BF/FE = ED / DA, which means BF = ED * FE / DA = 1 * 1 / X = 1 / X.
Pythagorean Theorem: (AB)^2 = (AC)^2 + (BC)^2
5^2 = (X + 1)^2 + ((X + 1) / X)^2
25 X^2 = X^2 (X + 1)^2 + (X + 1)^2 = (X^2 + 1) (X^2 + 2X + 1) = X^4 + 2 X^3 + 2 X^2 + 2 X + 1
X^4 + 2 X^3 - 23 X^2 + 2 X + 1 = 0
There is a "generic" solution for quartic equations, but I broke out LibreCalc and applied Newton-Raphson to get X = 0.227205.
I just realized...there are two possible answers; rotate the image 90% counterclockwise, then reflect it through the vertical axis.
The other answer = 1 / X = 3.838501
Quote: ThatDonGuy
Label the vertices of the triangle A, B, C such that AB is the hypotenuse and AC is the vertical (i.e. AC has length X + 1).
Label the remaining vertices of the square D, E, F such that CDEF is the square (i.e. D is on AC, E is on AB, abd F is on BC).
ADE is similar to EFB, so BF/FE = ED / DA, which means BF = ED * FE / DA = 1 * 1 / X = 1 / X.
Pythagorean Theorem: (AB)^2 = (AC)^2 + (BC)^2
5^2 = (X + 1)^2 + ((X + 1) / X)^2
25 X^2 = X^2 (X + 1)^2 + (X + 1)^2 = (X^2 + 1) (X^2 + 2X + 1) = X^4 + 2 X^3 + 2 X^2 + 2 X + 1
X^4 + 2 X^3 - 23 X^2 + 2 X + 1 = 0
There is a "generic" solution for quartic equations, but I broke out LibreCalc and applied Newton-Raphson to get X = 0.227205.
I just realized...there are two possible answers; rotate the image 90% counterclockwise, then reflect it through the vertical axis.
The other answer = 1 / X = 3.838501
I agree! Good point about there being two possible answers. I got to the same fourth-order equation and then used Excel's "goal seek" function to get a numeric answer.

In this age of covid, a small group of worshippers don masks and form a prayer circle on the lawn beside their church.
:strip_icc()/pic5676800.png)
If 8 people stand in a circle with six feet of required social distance between them (along a chord):
1) What is the circumference of the circle?
2) What is the diameter of the circle?
3) How far in a straight line (chord) is Person A from Person C?
4) The prayer circle is formed on a square lawn measuring 25x25 feet. What is the maximum number of people who could stand in the circle and still be 6 feet apart?
Quote: Gialmere
In this age of covid, a small group of worshippers don masks and form a prayer circle on the lawn beside their church.
If 8 people stand in a circle with six feet of required social distance between them (along a chord):
1) What is the circumference of the circle?
2) What is the diameter of the circle?
3) How far in a straight line (chord) is Person A from Person C?
4) The prayer circle is formed on a square lawn measuring 25x25 feet. What is the maximum number of people who could stand in the circle and still be 6 feet apart?
Been a while, so hopefully I'm thinking on the right lines.....
1) C = 49.57ft
2) d = 15.78ft
3) AC cord = 11.15ft (2*7.89) sin(.785 radians)
4) 12 people at most.....if we went to 13 people then we would go slightly over the radius of 12.5.....12.62 would be the radius for 13 people
radius = 3/sin(22.5) = 7.839377789
1. 2*pi*radius = 6*pi/sin(22.5) = 49.2563
2. 2*radius = 6/sin(22.5) = 15.6788
3. sqrt(2)*radius = 3*sqrt(2)/sin(22.5) = 11.0866
If this are right, I'll think about #4.
Quote: Gialmere
In this age of covid, a small group of worshippers don masks and form a prayer circle on the lawn beside their church.
If 8 people stand in a circle with six feet of required social distance between them (along a chord):
1) What is the circumference of the circle?
2) What is the diameter of the circle?
3) How far in a straight line (chord) is Person A from Person C?
4) The prayer circle is formed on a square lawn measuring 25x25 feet. What is the maximum number of people who could stand in the circle and still be 6 feet apart?
No 4
sinθ > 3/12.5
θ >13.8865
2θ > 27.773
Max people < 360/27.773
Max people < 12.962
Max people = 12
Again, I don't really understand what is "stand in the circle" .... I assumed stand along the circle circumference.
Quote: IAchance5Been a while, so hopefully I'm thinking on the right lines.....
Since the chord between 2 people is 6, then the radius of circle will be 7.89ft (6/(2 sin(.39 radians))
1) C = 49.57ft
2) d = 15.78ft
3) AC cord = 11.15ft (2*7.89) sin(.785 radians)
4) 12 people at most.....if we went to 13 people then we would go slightly over the radius of 12.5.....12.62 would be the radius for 13 people
1) Very close
2) Very close
3) Very close
4) Correct!
Quote: Wizard
radius = 3/sin(22.5) = 7.839377789
1. 2*pi*radius = 6*pi/sin(22.5) = 49.2563
2. 2*radius = 6/sin(22.5) = 15.6788
3. sqrt(2)*radius = 3*sqrt(2)/sin(22.5) = 11.0866
If this are right, I'll think about #4.
1) Correct!
2) Correct!
3) Correct!
Quote: ssho88No 4
sinθ > 3/12.5
θ >13.8865
2θ > 27.773
Max people < 360/27.773
Max people < 12.962
Max people = 12
Again, I don't really understand what is "stand in the circle" .... I assumed stand along the circle circumference.
4) Correct!
---------------------------------

<Insert your own prayer circle punchline here>
Call the worshipers A - M
With an odd number, there is nobody directly opposite A. Which means the people on the far side (#7=G & #8=H) are set in some from the opposite of the circle. i.e.
Assume the square is from y=+12.5 ft to -12.5 ft
Assume A is at the top border of the square (0,12.5)
With N=13, radius is r = 3/sin(.5*360/13) = 12.53574441 ft.
So center of circle would be at (0,-0.0357441)
The (horizontal) cord between the 7th person (G) and 8th person (H) is a distance of r * cos(.5*360/13) = 12.17147846 below the center of the circle at y=-12.20722256 ft. ...(from x = +3ft to -3ft for G & H respectively)
Thus G & H are still on the square lawn, even though the imaginary circle they are standing on (diameter = 2*12.5357441 = 25.07148882) extends out of the square.
If they hold hands along the cord (which seems likely), I think 13 fit entirely on the lawn.
If their arms curve along the circle, they are all standing on the lawn, but their arms would extend to an area above the boundary.....which I might argue the prayer "circle" is still standing in the square lawn.
Only if you need to paint the entire circle on the lawn so they know where to stand do you get limited to 12
14 still doesn't seem to work

***Waiting for the marbles to come out!***
(Except for the one in the lower left who is checking out that sexy b**ch next to him!)
Quote: Gialmere4) The prayer circle is formed on a square lawn measuring 25x25 feet. What is the maximum number of people who could stand in the circle and still be 6 feet apart?
I'm also confused by what is being asked of #4. Must the worshippers stand on the circumference of a circle? May they stand inside of it? Why mention a square, can't you just say the diameter of the circle is 25 feet?
Quote: WizardYou put $1 in a bank account at a fixed interest rate of 10%, compounded monthly. Over an infinite period of time, what ratio of the time will the balance start with a 1?
Quote: WizardYou put $1 in a bank account at a fixed interest rate of 10%, compounded monthly. Over an infinite period of time, what ratio of the time will the balance start with a 1?
This is one of the ways they catch accounting fraud.
Quote: WizardYou put $1 in a bank account at a fixed interest rate of 10%, compounded monthly. Over an infinite period of time, what ratio of the time will the balance start with a 1?
Let I be the "interest multiplier" - the amount you multiply the principle by each compounding term.
If it takes A terms to get from 10^k to 2 x 10^k, then (10^k) x (I^A) = 2 x 10^k
I^A = 2
A log I =log 2
A = log 2 / log I
If it takes B terms to get from 2 x 10^k to 10^(k + 1), then (2 x 10^k) x (I^B) = 10 x 10^k
I^B = 5
B = log 5 / log I
The ratio is log 2 / (log 2 + log 5); using base 10 logarithms, log10 2 + log10 5 = 1, so the ratio is log10 2 = about 0.30103
Quote: Ace2I guess log(2) =~ 30.1%
Quote: ThatDonGuy
Let I be the "interest multiplier" - the amount you multiply the principle by each compounding term.
If it takes A terms to get from 10^k to 2 x 10^k, then (10^k) x (I^A) = 2 x 10^k
I^A = 2
A log I =log 2
A = log 2 / log I
If it takes B terms to get from 2 x 10^k to 10^(k + 1), then (2 x 10^k) x (I^B) = 10 x 10^k
I^B = 5
B = log 5 / log I
The ratio is log 2 / (log 2 + log 5); using base 10 logarithms, log10 2 + log10 5 = 1, so the ratio is log10 2 = about 0.30103
I agree!
Mean = Integra[ x *f(x) dx] ?

Another table game designer consults you for your math skills. This one is working on a casino version of the popular bar game "Ship, Captain & Crew".
SCC is played with five standard dice. A player gets three rolls to score points. Before points can be scored, however, the player must first roll a ship (6), captain (5) and a crew (4), and they must be rolled in that specific order (or simultaneously).
For example, if the player started with a roll of 6, 4, 3, 2, 2 the player would set aside the 6 (ship) and re roll the other four dice. The player could not keep the 4 (crew) because he doesn't have a captain (5) yet. If the next roll was a 6, 5, 4, 4 the player would then set aside the 5 and, since he now has a captain, one of the 4s as his crew. The remaining dice (6, 4) would become his cargo with a point total of 10.
The designer envisions a craps like game with all players betting on a single shooter's three rolls. Although he has many side bet ideas, to get started he needs to work out the main (sort of pass line) bet.
What is the probability that a shooter (using the SCC nestled conditions rules) will get a 6, 5 and 4 in three rolls?
If I'm not being clear, here is a short video on how to play...
R1 R2 R3 Pr (1) Pr(2) Pr(3) Total
654 --- --- 0.0046 1.0000 1.0000 0.0046
--- 654 --- 0.4019 0.0046 1.0000 0.0019
--- --- 654 0.4019 0.4019 0.0046 0.0007
65 4 --- 0.0161 0.1667 1.0000 0.0027
65 --- 4 0.0161 0.5787 0.1667 0.0016
--- 65 4 0.1317 0.0161 0.1667 0.0004
6 54 --- 0.0329 0.0278 1.0000 0.0009
6 --- 54 0.0329 0.4823 0.0278 0.0004
--- 6 54 0.4019 0.0329 0.0278 0.0004
6 5 4 0.0329 0.0965 0.1667 0.0005
0.0141 total
rsactuary - the only way to format columns is to use tables
For instance initially throwing 5 dice, you can get
6-only : 2101
6 and 5: 1320
6 5 and 4 : 1230
miss : 3125
Rinse and repeat for using four dice trying to get 5 4 and three dice to get 4.
Work out all ways to get passes and fails, check it adds up to 77763.
Pass = 253 888 187 826
Fail = 216 296 796 750
Pr Pass = 53.9975%
| Outcome | Roll 1 | Roll 2 | Roll 3 | Perms 1 | Perms 2 | Perms 3 | Perms |
|---|---|---|---|---|---|---|---|
| Pass | 6 5 4 | any | any | 1 230 | 7 776 | 7 776 | 74 373 396 480 |
| Pass | 6 5 | 4 | any | 1 320 | 3 276 | 7 776 | 33 625 912 320 |
| Pass | 6 5 | miss | 4 | 1 320 | 4 500 | 3 276 | 19 459 440 000 |
| Pass | 6 | 5 4 | any | 2 101 | 1 812 | 7 776 | 29 603 325 312 |
| Pass | 6 | miss | 5 4 | 2 101 | 3 750 | 1 812 | 14 276 295 000 |
| Pass | 6 | 5 | 4 | 2 101 | 2 214 | 3 276 | 15 238 687 464 |
| Pass | miss | 6 5 4 | any | 3 125 | 1 230 | 7 776 | 29 889 000 000 |
| Pass | miss | 6 5 | 4 | 3 125 | 1 320 | 3 276 | 13 513 500 000 |
| Pass | miss | 6 | 5 4 | 3 125 | 2 101 | 1 812 | 11 896 912 500 |
| Pass | miss | miss | 6 5 4 | 3 125 | 3 125 | 1 230 | 12 011 718 750 |
| Total Pass | 0 | 0 | 0 | 253 888 187 826 | |||
| Fail | 6 5 | miss | miss | 1 320 | 4 500 | 4 500 | 26 730 000 000 |
| Fail | 6 | 5 | miss | 2 101 | 2 214 | 4 500 | 20 932 263 000 |
| Fail | 6 | miss | 5 | 2 101 | 3 750 | 2 214 | 17 443 552 500 |
| Fail | 6 | miss | miss | 2 101 | 3 750 | 3 750 | 29 545 312 500 |
| Fail | miss | 6 5 | miss | 3 125 | 1 320 | 4 500 | 18 562 500 000 |
| Fail | miss | 6 | 5 | 3 125 | 2 101 | 2 214 | 14 536 293 750 |
| Fail | miss | 6 | miss | 3 125 | 2 101 | 3 750 | 24 621 093 750 |
| Fail | miss | miss | 6 5 | 3 125 | 3 125 | 1 320 | 12 890 625 000 |
| Fail | miss | miss | 6 | 3 125 | 3 125 | 2 101 | 20 517 578 125 |
| Fail | miss | miss | miss | 3 125 | 3 125 | 3 125 | 30 517 578 125 |
| Total FAIL | 0 | 0 | 0 | 216 296 796 750 |
Quote: charliepatrickRather than look at states just look at all the ways to get there and how many of 7776 ways to throw five dice results in the required outcome.
For instance initially throwing 5 dice, you can get
6-only : 2101
6 and 5: 1320
6 5 and 4 : 1230
miss : 3125
Rinse and repeat for using four dice trying to get 5 4 and three dice to get 4.
Work out all ways to get passes and fails, check it adds up to 77763.
Pass = 253 888 187 826
Fail = 216 296 796 750
Pr Pass = 53.9975%
Outcome Roll 1 Roll 2 Roll 3 Perms 1 Perms 2 Perms 3 Perms Pass 6 5 4 any any Pass 6 5 4 any Pass 6 5 miss 4 Pass 6 5 4 any Pass 6 miss 5 4 Pass 6 5 4 Pass miss 6 5 4 any Pass miss 6 5 4 Pass miss 6 5 4 Pass miss miss 6 5 4 Total Pass Fail 6 5 miss miss Fail 6 5 miss Fail 6 miss 5 Fail 6 miss miss Fail miss 6 5 miss Fail miss 6 5 Fail miss 6 miss Fail miss miss 6 5 Fail miss miss 6 Fail miss miss miss Total FAIL
Correct! Very good.
-------------------------------------
The barman says, ďWe donít serve time travelers in here.Ē
A time traveler walks into a bar.

You are entering amounts in the check register but forgot to write down who received them.
If the optometrist got a check for $20.20, what person (1 - 12) received a check in each of the amounts listed (a - n)?
1. calendar vendor
2. casino worker
3. deer hunter
4. electrician
5. golf instructor
6. history teacher
7. IRS agent.
8. jet pilot.
9. mathematician
10. paramedic
11. piano tuner
12. soap maker.
a. $.18
b. $.88
c. $1.20
d. $3.14
e. $3.65
f. $7.11
g. $7.47
h. $9.11
i. $10.40
j. $14.92
m. $30.30
n. $99.44
2. casino worker $7.11 (always open)
3. deer hunter $30.30 (shotgun)
4. electrician $1.20 (volts)
5. golf instructor $.18 (holes)
6. history teacher $14.92 (Columbus)
7. IRS agent. $10.40 (form)
8. jet pilot. $7.47 (plane)
9. mathematician $3.14 (Pi)
10. paramedic $9.11 (emergency)
11. piano tuner $.88 (keys)
12. soap maker. $99.44 (ivory pure)
1. calendar vendor --> e. $3.65
2. casino worker -----> f. $7.11
3. deer hunter ------> m. $30.30*
4. electrician -------> c. $1.20
5. golf instructor ---> a. $.18
6. history teacher --> j. $14.92
7. IRS agent. -------> i. $10.40
8. jet pilot. ---------> g. $7.47
9. mathematician --> d. $3.14
10. paramedic -----> h. $9.11
11. piano tuner ----> b. $.88
12. soap maker ----> n. $99.44
* You should have paid him $30.06 -- you'd have literally gotten more bang for your buck!
Quote: IAchance5No Interest Theory formulas needed.....
1. calendar vendor $3.65 (days)
2. casino worker $7.11 (always open)
3. deer hunter $30.30 (shotgun)
4. electrician $1.20 (volts)
5. golf instructor $.18 (holes)
6. history teacher $14.92 (Columbus)
7. IRS agent. $10.40 (form)
8. jet pilot. $7.47 (plane)
9. mathematician $3.14 (Pi)
10. paramedic $9.11 (emergency)
11. piano tuner $.88 (keys)
12. soap maker. $99.44 (ivory pure)
Quote: Joeman
1. calendar vendor --> e. $3.65
2. casino worker -----> f. $7.11
3. deer hunter ------> m. $30.30*
4. electrician -------> c. $1.20
5. golf instructor ---> a. $.18
6. history teacher --> j. $14.92
7. IRS agent. -------> i. $10.40
8. jet pilot. ---------> g. $7.47
9. mathematician --> d. $3.14
10. paramedic -----> h. $9.11
11. piano tuner ----> b. $.88
12. soap maker ----> n. $99.44
* You should have paid him $30.06 -- you'd have literally gotten more bang for your buck!
Correct!
------------------------------------
I asked my girlfriend what sort of books she's interested in.
She said check books.
Quote: GialmereI asked my girlfriend what sort of books she's interested in.
She said check books.
I can't be overdrawn; I still have checks in my checkbook!

0 1 2 3 4 5 6 7 8 9
The object of this puzzle is to write a ten-digit number beneath the digits above using the following criteria...
The digit you place below the 0 is both the first digit of the number and also tells how many 0s are in the number.
The digit you place below the 1 is both the second digit of the number and also tells how many 1s are in the number. And so on to the digit below the 9 which is both the last digit of the number and tells how many 9s the number contains.
For example, if you place a 2 beneath the 0, you are saying that the number will be 2 billion something, that the number will contain two 0s and that the digit you place below the 2 will be 1 or more since the number now contains a 2.
You may use a given digit (including 0) as many times as you wish, or not at all.
What is the unique ten-digit number?
The digits must add up to 10. Thus:
0 1 2 3 4 5 6 7 8 9
6 2 1 0 0 0 1 0 0 0
6 2 1 0 0 0 1 0 0 0
Quote: gordonm888
The digits must add up to 10. Thus:
0 1 2 3 4 5 6 7 8 9
6 2 1 0 0 0 1 0 0 0
Quote: charliepatrickThere are a large number of zeroes, say N, so N is the first digit. There is (probably) only one of those (otherwise there would be more than 10 digits in the number), so there is a 1 under N. There is now at least one "1", so there is a number under 1, however it can't be 1 (as there would now be two of them), so it has to be 2 and a "1" under 2. From this there are six zeroes so the leading digit is 6.
6 2 1 0 0 0 1 0 0 0
Correct!
----------------------------------------


