Find the radius puzzle #2
Poll
 | 2 votes (25%) | ||
| | 4 votes (50%) | ||
| No votes (0%) | |||
| No votes (0%) | |||
| No votes (0%) | |||
| | 4 votes (50%) | ||
| | 1 vote (12.5%) | ||
| | 2 votes (25%) | ||
| | 1 vote (12.5%) | ||
| No votes (0%) |
8 members have voted
February 19th, 2020 at 7:40:39 AM
permalink
In our continued celebration of 2020, the year of math appreciation, I present the following geometry problem.
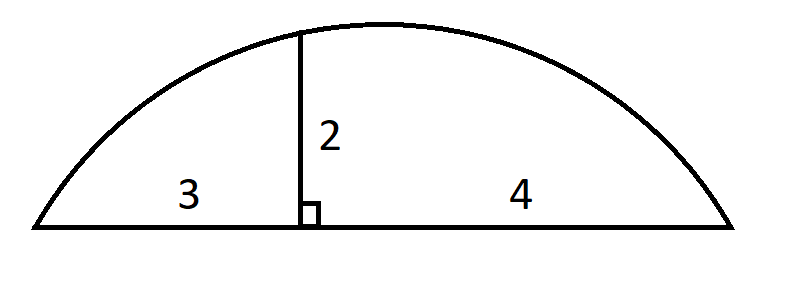
The following diagram shows a chord drawn across a circle. From a point on the chord, a perpendicular line is drawn to another point on the same circle. Distances are shown in the diagram above.
What is the radius of the circle?
Usual rules:
1. Please don't just plop a URL to a solution elsewhere until a winner here has been declared.
2. All those who have won a beer previously are asked to not post answers or solutions for 24 after this posting. This rule has been violated by past winners the previous two problems. Past winners who must chime in early, may PM me.
3. Beer to the first satisfactory answer and solution, subject to rule 2.
4. Please put answers and solutions in spoiler tags.
The following diagram shows a chord drawn across a circle. From a point on the chord, a perpendicular line is drawn to another point on the same circle. Distances are shown in the diagram above.
What is the radius of the circle?
Usual rules:
1. Please don't just plop a URL to a solution elsewhere until a winner here has been declared.
2. All those who have won a beer previously are asked to not post answers or solutions for 24 after this posting. This rule has been violated by past winners the previous two problems. Past winners who must chime in early, may PM me.
3. Beer to the first satisfactory answer and solution, subject to rule 2.
4. Please put answers and solutions in spoiler tags.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
February 19th, 2020 at 1:49:13 PM
permalink
Is the question being asked clear?
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
February 19th, 2020 at 1:58:17 PM
permalink
Crystal.Quote: WizardIs the question being asked clear?
It looks like it should be easy.... But, I'm getting in a right mess trying :o)
Psalm 25:16
Turn to me and be gracious to me, for I am lonely and afflicted.
Proverbs 18:2
A fool finds no satisfaction in trying to understand, for he would rather express his own opinion.
February 19th, 2020 at 2:51:19 PM
permalink
Placeholder while I paste my workings 5.409771
Psalm 25:16
Turn to me and be gracious to me, for I am lonely and afflicted.
Proverbs 18:2
A fool finds no satisfaction in trying to understand, for he would rather express his own opinion.
February 19th, 2020 at 2:59:35 PM
permalink
Quote: OnceDearNot sure if I'm a beer recipient, so workings PM'd to Wizard.Placeholder while I paste my workings 5.409771
Negative. No beer for you yet. Since you're on the wagon, I hope a spotted dick will suffice.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
February 19th, 2020 at 3:06:28 PM
permalink
Off to check my algebra.....
Psalm 25:16
Turn to me and be gracious to me, for I am lonely and afflicted.
Proverbs 18:2
A fool finds no satisfaction in trying to understand, for he would rather express his own opinion.
February 19th, 2020 at 3:28:29 PM
permalink
Quote: OnceDearOff to check my algebra.....
I had messed up in algebra. Here's my solution after some checking and fixing..
Label the 3 points ABC from left to right.
AC=7.
The line AC is distance z vertically from the circle's centre
Half way along AC is at 3.5 and is above the origin of the circle.
For A, it's offset 3.5 to the left of the centre of the circle, so x1= -3.5 and y1=z
For B, it's offset 0.5 to the left of the centre of the circle so x2= -0.5 and y2=z+2
For C, it's offset 3.5 to the right of the centre of the circle, so x3= 3.5 and y3=z
x1^2 +y1^2 =x2^2 +y2^2 = x3^2 +y3^2 =r^2 ( Pythagoras applied to any Right angle triangle made from centre to point xy on the circle of radius r where x and y coordinates from the centre)
(-3.5)^2 + z^2 = (-0.5)^2 +(z+2)^2
(-3.5)^2 + z^2 = (-0.5)^2 + z^2 +4z +4
(-3.5)^2 +z^2 -(-0.5)^2 -z^2 -4z -4 = 0
z^2 - z^2 - 4z = (-0.5)^2-(-3.5)^2 +4
-4z = -8
z= 2
now we know z
x1^2 +y1^2=r^2
(-3.5)^2+z^2=r^2
(-3.5)^2+2^2=r^2
r^2=16.25
r=4.03112887415
AC=7.
The line AC is distance z vertically from the circle's centre
Half way along AC is at 3.5 and is above the origin of the circle.
For A, it's offset 3.5 to the left of the centre of the circle, so x1= -3.5 and y1=z
For B, it's offset 0.5 to the left of the centre of the circle so x2= -0.5 and y2=z+2
For C, it's offset 3.5 to the right of the centre of the circle, so x3= 3.5 and y3=z
x1^2 +y1^2 =x2^2 +y2^2 = x3^2 +y3^2 =r^2 ( Pythagoras applied to any Right angle triangle made from centre to point xy on the circle of radius r where x and y coordinates from the centre)
(-3.5)^2 + z^2 = (-0.5)^2 +(z+2)^2
(-3.5)^2 + z^2 = (-0.5)^2 + z^2 +4z +4
(-3.5)^2 +z^2 -(-0.5)^2 -z^2 -4z -4 = 0
z^2 - z^2 - 4z = (-0.5)^2-(-3.5)^2 +4
-4z = -8
z= 2
now we know z
x1^2 +y1^2=r^2
(-3.5)^2+z^2=r^2
(-3.5)^2+2^2=r^2
r^2=16.25
r=4.03112887415
Psalm 25:16
Turn to me and be gracious to me, for I am lonely and afflicted.
Proverbs 18:2
A fool finds no satisfaction in trying to understand, for he would rather express his own opinion.
February 19th, 2020 at 3:48:04 PM
permalink
Two coordinates will solve the problem, (-0.5, 2+y) and (3.5, y)
(-0.5)^2+ (2+y)^2 = r^2..........A
(3.5)^2 + y^2 = r^2...................B
A - B :-
4y+4 =12 = 0
y=2, r = (65)^0.5/2
(-0.5)^2+ (2+y)^2 = r^2..........A
(3.5)^2 + y^2 = r^2...................B
A - B :-
4y+4 =12 = 0
y=2, r = (65)^0.5/2
Last edited by: ssho88 on Feb 19, 2020
February 19th, 2020 at 3:50:20 PM
permalink
We concur, though your calcs seem simpler than mine. Your last line ( the big number?) seems a bit of a leap to my addled brain.Quote: ssho88Two coordinates will solve the problem, (-0.5, 2+y) and (3.5, y)
(-0.5)^2+ (2+y)^2 = r^2..........A
(3.5)^2 + y^2 = r^2...................B
A - B :-
4y+4 =12 = 0
y=2, r^2 = (65)^0.5/2
Psalm 25:16
Turn to me and be gracious to me, for I am lonely and afflicted.
Proverbs 18:2
A fool finds no satisfaction in trying to understand, for he would rather express his own opinion.
February 19th, 2020 at 4:24:12 PM
permalink
Quote: OnceDearI had messed up in algebra. Here's my solution after some checking and fixing..
Label the 3 points ABC from left to right.
AC=7.
The line AC is distance z vertically from the circle's centre
Half way along AC is at 3.5 and is above the origin of the circle.
For A, it's offset 3.5 to the left of the centre of the circle, so x1= -3.5 and y1=z
For B, it's offset 0.5 to the left of the centre of the circle so x2= -0.5 and y2=z+2
For C, it's offset 3.5 to the right of the centre of the circle, so x3= 3.5 and y3=z
x1^2 +y1^2 =x2^2 +y2^2 = x3^2 +y3^2 =r^2 ( Pythagoras applied to any Right angle triangle made from centre to point xy on the circle of radius r where x and y coordinates from the centre)
(-3.5)^2 + z^2 = (-0.5)^2 +(z+2)^2
(-3.5)^2 + z^2 = (-0.5)^2 + z^2 +4z +4
(-3.5)^2 +z^2 -(-0.5)^2 -z^2 -4z -4 = 0
z^2 - z^2 - 4z = (-0.5)^2-(-3.5)^2 +4
-4z = -8
z= 2
now we know z
x1^2 +y1^2=r^2
(-3.5)^2+z^2=r^2
(-3.5)^2+2^2=r^2
r^2=16.25
r=4.03112887415
I agree!!! Congratulations, you have finally earned a beer. Substitutions for people on the wagon are gladly accommodated. Hope to pay off my debt soon.
The formula in your solution I did not know. My solution is quite a bit longer, but requires knowing only the Pythagorean formula and it is applied once only.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
February 19th, 2020 at 5:21:06 PM
permalink
Here is my solution (pdf).
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
February 19th, 2020 at 6:33:56 PM
permalink
Quote: WizardMy solution is quite a bit longer, but requires knowing only the Pythagorean formula and it is applied once only.
I am so glad to hear this. While I have yet to solve any of these math problems, I thoroughly enjoy thinking them through. And while I have yet to solve, I was trying to apply the Pythagorean formula this afternoon. I just couldn't get there first. Thanks!
February 19th, 2020 at 8:24:54 PM
permalink
The key to my solution is any three non-linear points lay on exactly one circle. Taking the three points I identified, one can find the circle.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
February 19th, 2020 at 9:22:56 PM
permalink
You don't need to know the formula for CIRCLE, just assumed center of circle, O with coordinate (0,0), then coordinate C( -0.5, y+2), coordinate B(3.5, y)
Then length OC = OB, solve for y and r(OB or OC).
Then length OC = OB, solve for y and r(OB or OC).
February 20th, 2020 at 2:33:40 AM
permalink
Assume the centre is z lower than the line AB and consider OB. Then the radius of the circle is the hypoteneuse with sides z and 3.5. Similarly the radius OC is the hypoteneuse with sides (z+2) and .5.
So r = SQRT (z^2 + 3.5^2) = SQRT ((z+2)^2 + .5^2).
So z^2 + 12.25 = z^2 + 4z + 4 + .25. Subtracting z^2-4 from both sides, 8=4z. z = 2.
So radius = SQRT(4 + 12.25) = SQRT (16.25).
So r = SQRT (z^2 + 3.5^2) = SQRT ((z+2)^2 + .5^2).
So z^2 + 12.25 = z^2 + 4z + 4 + .25. Subtracting z^2-4 from both sides, 8=4z. z = 2.
So radius = SQRT(4 + 12.25) = SQRT (16.25).
