Thread Rating:
Poll
 | 4 votes (57.14%) | ||
| No votes (0%) | |||
 | 1 vote (14.28%) | ||
| No votes (0%) | |||
 | 2 votes (28.57%) | ||
 | 1 vote (14.28%) | ||
 | 2 votes (28.57%) | ||
 | 2 votes (28.57%) | ||
 | 1 vote (14.28%) | ||
 | 4 votes (57.14%) |
7 members have voted
Usual rules apply:
1. No searching
2. No posting links to solutions elsewhere.
3. Please put answers and solutions in spoiler tags until I announce a satisfactory solution.
4. Beer to the first satisfactory answer and solution.
5. Those who have won a beer in the last year may not play for the 24 hours following this posting.
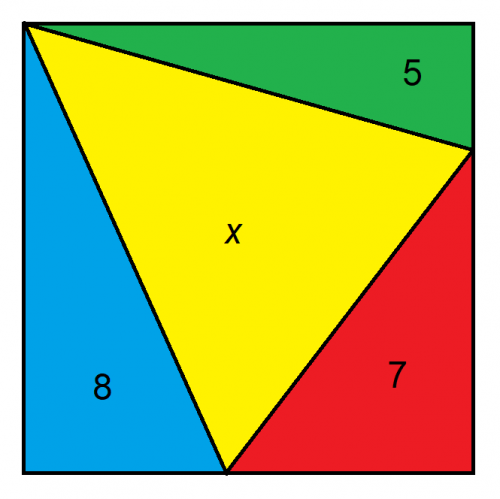
No. It can't be.Quote: rsactuaryIs the yellow triangle an equilateral triangle? or does that have to be determined?
I'm doing it, but somebody is sure to beat me to it.
Quote: WizardThis post was removed in the interests of giving others who haven't won a beer a chance at it. I copied and pasted the text to Don. Those who haven't won a beer yet have until 24 hours since the OP to solve it.
Hopefully nobody will cheat who may remember Don's post.
Quote: rsactuaryIs the yellow triangle an equilateral triangle? or does that have to be determined?
It has to be determined.
Quote: BigJerLol. Are the numbers the area or a side of the triangles?
I think it has to be area.
x = L^2 - 20
So, the key is solving for L^2, which we can get by solving a set of equations for the areas of the three triangles. The blue and green triangles both have a height of L. We can call their respective bases b1 and b2.
1/2 L x b1 = 8
1/2 L x b2 = 5
Solving each for the base in terms of L, we get:
b1 = 16/L
b2 = 10/L
The base and height of the red triangle would be L - b1 and L - b2. So, its area can be represented by:
1/2 (L - b1) x (L - b2) = 7 or
L^2 - Lb1 - Lb2 + 10/L x 16/L = 14
Substituting from above, we get:
L^2 - L(16/L) - L(10/L) + (16/L)(10/L) = 14
Which, after reducing, rearranging, and finally multiplying all terms by L^2, we get:
L^4 - 40L^2 + 160 = 0
Using the quadratic equation**, we can solve for L^2, which would be an area for the square of 35.49. Subtracting out the area of the known triangles, we get x = 15.49.
** FULL DISCLOSURE: I mis-remembered the formula for the quadratic equation (it's been quite a while...), and when my first answer didn't make sense, I had to look up the formula. Not sure if this would disqualify me for the beer.
edit, I got my labelling wrong when I scribbled it out. correcting...
Let base side of square be y
Let short redgreen side be g
Let short blue side be b
Let short green side be g1 red side be r1
Let long green side be g2 red side be r2 (Not hypoteneuse)
Using area of triangle = 1/2 base x height
5=g.y/2
y=10/g
8=b.y/2
y=16/b
Looking at red triangle of area =7=r1.r2/2
14=r1.r2
but r1=y-b and r2=y-g
14=(y-b)(y-g)
14=(y-16/y).(y-10/y)
14=y^2-16-10+160/y^2
40=y^2+160/y^2
Now y^2 is the area of the square. Call y^2 S
0=S+160/S-40
multiply both sides by S
0=S^2-40S+160
a simple quadratic with solutions
S=35.49193338483
or
S=4.5080666151703
Now we reject the second answer because the total area is at least the sum of 8,5,7
So total square area is 35.49
therefore area x=35.49-8-7-5=15.49
I'm off to check my workings now. Just wanted to get it posted
I honestly thought someone else would post the answer while I was typing my response! Hey, you can't drink the beer anyway, right? ;-)Quote: OnceDearJoeman. You absolute ( insert expletive) :o)
So did I, but I was right!Quote: JoemanI honestly thought someone else would post the answer while I was typing my response! Hey, you can't drink the beer anyway, right? ;-)
Pah! I never received the last pint he sent me. I keep checking the mail for US parcel. I guess it never cleared customs.
Quote: BigJerLol. Are the numbers the area or a side of the triangles?
Area.
Quote: OnceDearJoeman. You absolute ( insert expletive) :o) You beat me by 11 minutes, but we seem to agree.
Yes, I agree that Joe got it first. Cheers, Joe, I owe you a beer. Commiserations to OD. I'll still buy you one, preferably in the wee village of Shackleford, but not for this reason.


