Parrondo's Paradox: Two Losers Make a Winner

I recently saw this Vsauce2 video about Parrondo's Paradox, and while I normally really like Vsauce's content, I found the explanation in the video really lacking. It has over a million views, so I figured I might not be the only one who on the forum encountered it, and thought a thread might help illuminate what's really going on.

The "paradox" is that you can define two games, A and B, that are both negative EV on their own; playing either continuously will eventually result in a loss. However, you end up winning in the long-run by simply switching back and forth between the games.

That might sound unremarkable to anyone who has Wonged into a positive count and then switched to vulturing a multi-state slot; blackjack and slots are both -EV overall, but you can make money by judiciously choosing when to play each one. The difference here is that you end up winning even if you randomly choose which game to play each turn, or use a simple pattern like AABBAABB that doesn't take into account what state the game is in (what cards have been dealt, what bonuses are in play, etc.). In fact, Parrondo's original example (which he beautifully explains on this website) doesn't even have "states" — you can set up both games using only even-money bets on a total of three different biased coins. The diagram below maps it out (notation — X(t) is your bankroll at any given time, which will always be an integer since all wins and losses are 1 unit. The green coin favors the player, while the red coins favor the house):



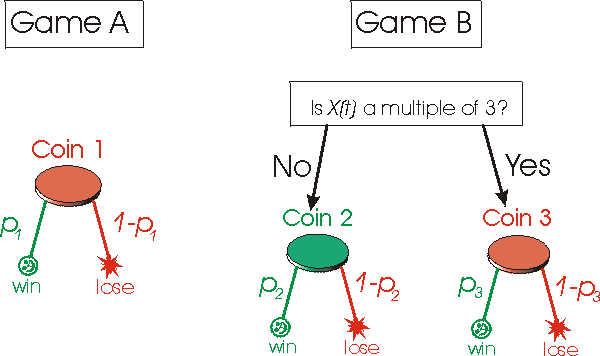
And below is a plot of your capital growth over time using various strategies (notation — the line labeled [3, 2] is your profit from playing game A for 3 rounds, then game B for 2 rounds, then A for 3 again, B for 2 again, etc.):


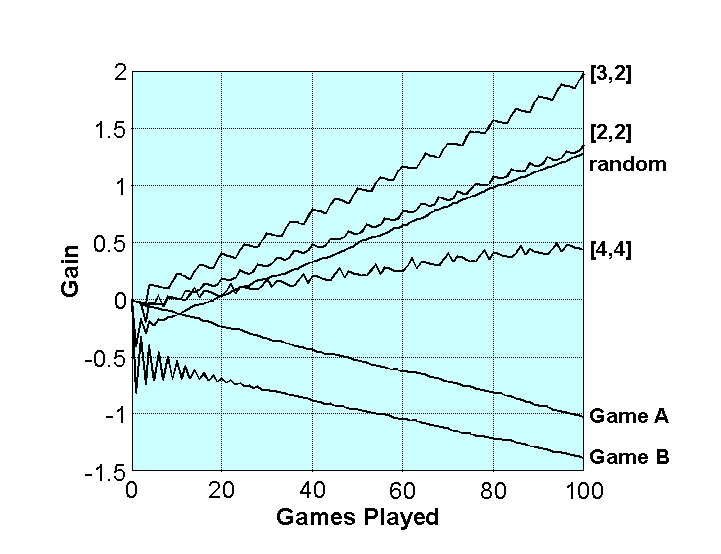
There's a lot more to say about this, including its connection to thermodynamics and the Brownian Ratchet, as well as explaining why Parrondo's Game B is actually -EV on its own (it might look +EV at first glance). But I'd much rather this be a discussion than a monologue, so I'll leave it there for now. Would love to hear any thoughts folks have on this.

I never found Parrondo's Paradox very interesting. It is actually three games, one of which is positive EV. It gets played often enough to make the overall average positive.

a fair coin has a slight bias towards its initially upwards face.

a die can be milled to a biased dimension but is almost impossible to gain financially from it.

THREE games????

It seems that one of the games must have a periodic oscillatory nature such that it swings from positive EV to negative EV due to some predictable underlying reason. And, the player simply plays this game when it is positive EV and 'Wongs out" to the first game when the second game becomes wildly negative in its expected value.

Okay, I understand this. Interesting, but not particularly profound in my opinion.

There was a fiction book written with this as the main plot point. I forget the title, but it's about a guy who finds a way to apply Parrondo's paradox to playing craps, and he becomes a millionaire gambling in casinos.

Fwiw: Ask the Wizard 149 starts with a discussion of parrondo's paradox.

https://wizardofodds.com/ask-the-wizard/149/

Quote: TigerWu

, and he becomes a millionaire gambling in casinos.

As you said, FICTION.

Quote: TigerWu

There was a fiction book written with this as the main plot point. I forget the title, but it's about a guy who finds a way to apply Parrondo's paradox to playing craps, and he becomes a millionaire gambling in casinos.

I read that and am struggling to remember the name. Pretty good read. However, unless we're talking about different books, that wasn't exactly the plot. As I recall I guy buys a #@$% betting system referring to Parrondo somehow, actually wins with it on luck alone, some goons mixed up in organized crime get interested, and that's as far as I'll go without ruining it too much.

Quote: Wizard

I read that and am struggling to remember the name. Pretty good read. However, unless we're talking about different books, that wasn't exactly the plot. As I recall I guy buys a #@$% betting system referring to Parrondo somehow, actually wins with it on luck alone, some goons mixed up in organized crime get interested, and that's as far as I'll go without ruining it too much.

We're probably talking about the same book; it's been about 15 years since I've read it. I figured out it's called "God Doesn't Shoot Craps."

Thirty dollars paperback; $0.99 Kindle version.

Quote: FleaStiff

Thirty dollars paperback; $0.99 Kindle version.

I did a review of it on this forum back when I was in my book review phase.

https://wizardofvegas.com/forum/off-topic/general/24574-god-doesnt-shoot-craps-btp-3/

Quote: FleaStiff

Thirty dollars paperback; $0.99 Kindle version.

There's multiple copies on eBay right now for under $10.

Quote: Wizard

I never found Parrondo's Paradox very interesting. It is actually three games, one of which is positive EV. It gets played often enough to make the overall average positive.

I agree that the overall paradox is pretty underwhelming, though I think that's in part just a failure of marketing. To me, the real "paradox" or at least the real interesting thing is that Game B isn't +EV when played on its own. Imagine the first step, the one that decides which coin you'll flip, consisted of rolling a die, where a 2 or 3 meant "crapping out" and getting ⅒ odds on your even-money bet (a -80% EV bet), while a 1, 4, 5, or 6 meant getting ¾ odds (a +50% EV bet). Taking the weighted average, the EV for the whole game would be -80%×⅓ + 50%×⅔ = +6.66%. At first, I naïvely thought that switching this die roll for Parrondo's actual rule (you get a ⅒ chance if your capital is divisible by 3, and a ¾ chance otherwise) wouldn't change anything, because, at least in the long-run, your bankroll (mod 3) should be randomly distributed, meaning it'd be divisible exactly ⅓ of the time. It's fascinating to me that when you actually play this out with a simulation or a Markov chain you get "stuck" alternating between 0 (mod 3) and 2 (mod 3) enough to make the game EV-neutral forever (or EV-negative if you decrease all the coin odds I gave a little, as Parrondo does). Usually patterns like that involving probabilistic events eventually give way to total randomness (like those pseudo-congruences we were discussing that inflate the divisibility (mod 11) of the partition numbers, but only temporarily).

But yea, when you look at it that way, throwing in Game A as "random noise" actually cancels out the paradox and makes things less interesting, since if Game B gets "reset" constantly, Parrondo's (mod 3) rule essentially becomes equivalent to the die roll and Game B essentially becomes +6.66%. In other words, they could have made the headline "Game B looks +EV but actually isn't when played continuously," which to me is interesting. But instead they went for "Game B is +EV as you'd expect as long as you don't play too long," since that is equivalent to the much sexier "Two losing strategies make a winner" as long as "not playing too long" consists of a switching to a slightly EV-negative activity like Game A.

Quote: beachbumbabs

Fwiw: Ask the Wizard 149 starts with a discussion of parrondo's paradox.

https://wizardofodds.com/ask-the-wizard/149/

Thanks Babs. I also now see that this has come up in other threads before; I should have checked that before starting a new one.

I did notice, though, that the Ask the Wizard response said that the paradox "has zero practical value in the casino" because your odds don't change based on the modulo of your bankroll. It's definitely for the best to dispel from the get-go the idea that you can use this to come up with some winning betting system, but that said, I'm not sure that the existence of games which are +EV for short sessions and -EV for long sessions is totally irrelevant to casinos.

First of all, a few years after Parrondo originally came up with the idea, he published a paper showing that you can get the same effect (and actually get more wiggle room for how much you can tweak the bets past EV-neutral) if Game B is a history-dependent Parrondo game. That is, it isn't the modulo of your bankroll that determines whether you get good or crappy odds in Game B—it's the outcome of the last round (or two). That's not too far off from how a "compensated" multi-state slot would work, where whether or not you just got a specific combination of symbols determines whether you are launched into a +EV bonus mode, and how much you've won recently affects your EV going forward. To be crystal clear: if you found such a slot, you could not beat it using Parrondo's paradox unless, along with a ton of other perfect conditions, it somehow "reset" each time a new player sat down. I don't know much about AP slots, but as far as I know most winning plays rely on the fact that that doesn't happen, which makes vulturing possible. Still, I'd be curious if there's ever been a play that took advantage of some software flaw which somehow allowed players to advantageously "reset" the game state; if so, you could model that with Parrondo's Paradox.

On the casino side, if you were cruel, you could also imagine using this in reverse to set-up a bait-and-switch play-thru bonus; set up a game like Game B, and allow players to do as many "short practice sessions" with fake money as they want, but have the balance from each session roll over so they can see it growing. You might even get some AP's to do the naïve EV calculation without a Markov chain and convince themselves it's a +EV play. Then require that they play through a large bankroll in a single session with their real money, and without the "noise" of constantly resetting that bankroll disappears.

This is purely speculative, but the paradox could even be a useful starting point for analyzing strategy in games like poker, where your winning a hand doesn't just increase your bankroll but also the size of your stack, which in turn affects the way others play against you and therefore the odds you have of winning subsequent hands. The paradox could be one way of analyzing how strategy for shootout tournaments, where your chips are constantly "reset" at each table, differs from strategy in cash games.

Quote: gordonm888

It seems that one of the games must have a periodic oscillatory nature such that it swings from positive EV to negative EV due to some predictable underlying reason. And, the player simply plays this game when it is positive EV and 'Wongs out" to the first game when the second game becomes wildly negative in its expected value.

Okay, I understand this. Interesting, but not particularly profound in my opinion.

You're definitely right that one game has to have a +EV and -EV mode, but, as I tried to explain in the OP, what makes this a paradox is that the player isn't choosing to 'Wong out' by observing what mode that game is in. They could choose whether to play Game A or Game B each round completely at random, without ever considering whether the EV for Game B will be positive or negative, and they will still win in the long run.

Quote: Wizard

"It's not whether you win or lose; it's whether or not you had a good bet."

That's really true, isn't it. It's the
quality of the bet that counts,
It's most important because if you
only make quality bets, you will
prevail in the end. How many
gamblers actually do that, or
even know what a quality bet
is.

>>> How many gamblers actually even know what a quality bet is.
Most gamblers are more concerned with a quality win!

Thank you for the post. I've been thinking about Parrando's Paradox for years since that video came out. I attempted it in the past, but then I realized that the house edge has to be 0.5% (or lower I presume). I clicked on your link because you wrote that you can set up the games only using even-money bets, but I didn't see that in any page on the website. I only see 50%, 10%, and 75% on all of the pages. Maybe I didn't look closely enough. Can you link the page that shows how to set up the games using only even-money bets? Also, do you know if your balance being a multiple of 3 is for any unit size, or do you have to account for different unit sizes? i.e., if I choose a unit size of 4, do I have to divide my bankroll by 4 to see if that number is divisible by 3, or is the divisible by 3 rule for any unit size? Lastly, do you know if B1 HAS to be a 9.5%-10% chance at 9:1 odds, or can it be an 11.1% chance with 8:1 odds? If you win at 9:1, your bankroll will be divisible by 3 again, but the 8:1 payout has a slightly better chance of hitting.

Thanks!

SilverCoin

I was the last person to reply to this thread, but I learned new information about Parrondo's Paradox. I was under the impression that all games would be paid out as if they were actual casino games e.g., the 74.5% bet being paid out at 4:3 and the 9.5% bet being paid out out at 9:1, but all of the games in Parrando's game have a 1:1 payout regardless of percentages. You either win $1 or you lose $1. This means that B2 is positive on its own. You have a 25.5% chance to lose $1 and a 74.5% chance to win $1. You can play B2 by itself and be positive. By this logic, B1 is INCREDIBLY negative. You have a 9.5% chance to win $1 and a 90.5% chance to lose $1. Parrando's game is only positive because the way that it's templated makes it so that you have a higher chance of playing B2 than B1 when played in certain orders. The order AABB is positive, BBABA is positive, but ABBB is negative. This means that you have a higher chance of playing B2 than B1 when playing in AABB order or BBABA order, but you have a higher chance of playing B1 when playing in ABBB order. The paradox is only that the two games together are positive if you decide which game to play at random. Switching back and forth in certain orders between games and being positive is not the paradox. Being positive at random is the paradox. It's a dead cause because no casino is going to make a game that pays 1:1 with a 74.5% bias towards the player.

-SilverCoin

There are situations in each-way betting in horse racing when two or more negative EV bets can be combined as multiples and become positive EV. When I first started reading about Parrondo's paradox I assumed that it might be referencing situations like that, but it's not.

Quote: blackjacklad

There are situations in each-way betting in horse racing when two or more negative EV bets can be combined as multiples and become positive EV. When I first started reading about Parrondo's paradox I assumed that it might be referencing situations like that, but it's not.
link to original post

I'm actually very interested in this topic. Do you have any references, or could you explain it? I've been thinking of betting on horses for a couple months now. I saw a video on youtube years ago where this gentleman explains all of his parameters for betting on horses, but I can't find that video anymore. I was positive the first time I went to a racing track because I bought the booklet of the upcoming races with all of the stats from previous races. I made very simple parameters on my own based on the booklet, but I want to find that video again so I can actually have a professional formula.

If you're not familiar with how each-way bets work, or how multiple/accumulator bets work, google will help you.

Imagine there are two horse races today, and I have my eye on a horse in each race. I have a model which I use to determine the fair odds, and therefore the expected value, of the win part and the place part of my each way bets. To keep it simple let's imagine the conditions are identical in each race, in terms of the odds and the place terms.

In each race, the horse has offered odds of 10.0, and the place terms are 1/4 paying 3 places, which means the offered odds of the place part of the bet are 3.25. I believe that the fair odds of the horse winning are 12, and the fair odds of the horse coming in the top 3 are 2.8. Therefore the EV of the win bet is 0.8333 (10/12) and the EV of the place bet is 1.161 (3.25/2.8). The win bet is a negative EV bet, and the place bet is a positive EV bet, but because this is an each way bet I have to place both at the same time, creating an each way bet with an EV of 0.997 (0.8333+1.161)/2.

The each way bet is negative EV. However, if I put the each way bets from each race into a double I create an each way bet with positive EV. This is because the positive compounding effect of putting positive EV bets together is stronger than the negative compounding effect of putting negative EV bets together.

The double each way bet consists of two bets - a win double, and a place double. The win double has an EV of 0.694 (0.833*0.833), and the place double has an EV of 1.347 (1.161*1.161), which means the each way double has an EV of 1.021 (0.694*1.347).

Quote: blackjacklad

If you're not familiar with how each-way bets work, or how multiple/accumulator bets work, google will help you.

Imagine there are two horse races today, and I have my eye on a horse in each race. I have a model which I use to determine the fair odds, and therefore the expected value, of the win part and the place part of my each way bets. To keep it simple let's imagine the conditions are identical in each race, in terms of the odds and the place terms.

In each race, the horse has offered odds of 10.0, and the place terms are 1/4 paying 3 places, which means the offered odds of the place part of the bet are 3.25. I believe that the fair odds of the horse winning are 12, and the fair odds of the horse coming in the top 3 are 2.8. Therefore the EV of the win bet is 0.8333 (10/12) and the EV of the place bet is 1.161 (3.25/2.8). The win bet is a negative EV bet, and the place bet is a positive EV bet, but because this is an each way bet I have to place both at the same time, creating an each way bet with an EV of 0.997 (0.8333*1.161).

The each way bet is negative EV. However, if I put the each way bets from each race into a double I create an each way bet with positive EV. This is because the positive compounding effect of putting positive EV bets together is stronger than the negative compounding effect of putting negative EV bets together.

The double each way bet consists of two bets - a win double, and a place double. The win double has an EV of 0.694 (0.833*0.833), and the place double has an EV of 1.347 (1.161*1.161), which means the each way double has an EV of 1.021 (0.694*1.347).
link to original post

I love hearing the math behind positive ev bets from passionate people. I understand all of the concepts, but I'm not very experienced with betting horses. I have my own thing going on with positive ev bets in other areas, but I definitely want to study up in the near future.