Poll
 | 3 votes (20%) | ||
 | 3 votes (20%) | ||
 | 1 vote (6.66%) | ||
| No votes (0%) | |||
| No votes (0%) | |||
 | 3 votes (20%) | ||
 | 1 vote (6.66%) | ||
 | 1 vote (6.66%) | ||
 | 3 votes (20%) | ||
 | 1 vote (6.66%) |
15 members have voted
Draw all homeomorphically irreducible trees of size n=10.
Here is my attempt to put it in plain simple English.
Using only straight lines, draw all figures where the sum of intersections and dead ends equals 10. You may not have any closed loops. You may also not have two equivalent figures. Any intersection must have at least three paths leading from it.
What do I mean by "equivalent," you might ask. It means if you can move the pieces, while leaving the intersections alone, any way you wish and it won't create any new figures.
I'll start you out with an example:
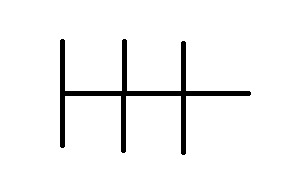
I'll just tell you there are a total of 10. Can you find the other 9? Please, no searching. There are a bunch of YouTube videos on this so it would be too easy to cheat. See if you're smarter than the whole MIT math department *ahem* by solving it yourself in less than two years.
The question for the poll is how many can you get?
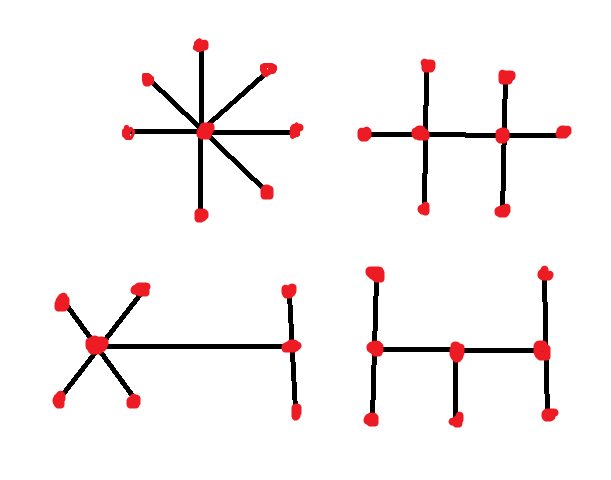
If the question were n=8 instead of n=10 then I get four possible answers, which are below. Note the eight red dots in each figure. Does that help?
Quote: RomesMS Paint and about 60 seconds later:

No. Because you have one point that has only two lines leaving from it. Any point must be an intersection of three or more points or a dead end. In other words, anything but 2.
edit: Bottom middle?
Quote: RomesWhich point? I only have 3 intersections, and all 3 have 3 lines coming out from the center.
edit: Bottom middle?
Yes, it was the bottom middle. However you're new spoiler pattern is good. For the benefit of everybody, we'll call my example pattern #1 and yours #2. Eight more to go.
Yeah, I'm one of those that didn't understand. And your n=8 example DOES clear things up.Quote: WizardOkay, two people have already voted they don't understand the question. I think asking it is harder than answering it.
If the question were n=8 instead of n=10 then I get four possible answers, which are below. Note the eight red dots in each figure. Does that help?
I gotta give this some thought.....
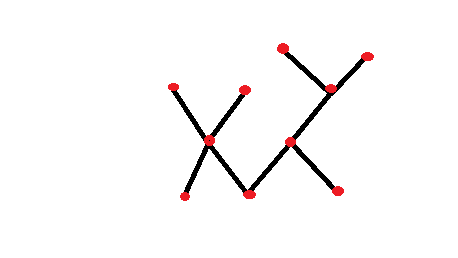
Quote: MathExtremistSo are the following two figures "equivalent" or not?
[spoiler][/spoiler]
Yes, they are. They call these things trees. In your example you could bend down the middle two branches on the top to the bottom. It would still be the same tree.
Quote: MathExtremistI need to know more about what "equivalent" means, but I can't look it up because nearly every reference to "homeomorphically irreducible" is to Good Will Hunting. So are the following two figures "equivalent" or not?
FWIW, as I understand it, your example is the same in both iterations, or equivalent. I could be wrong.
1 bar, 2 points. From each end, 4 more bars, like fingers. 10 total points. Same bar, with 3 and 5 bars extending. Same bar, with 2 and 6 points extending.
That's 3 examples, and if the ends were flipped or mirrored, I believe they would be equivalent, so it's only 3.
Quote: MathExtremistSo are the following two figures "equivalent" or not?
Ok, then I'm stuck on 9. I studied graph theory in college and I know about trees, I just don't know what "homeomorphically irreducible" means and I can't look it up without running the risk of having the answer spoon-fed to me.Quote:Yes, they are. They call these things trees. In your example you could bend down the middle two branches on the top to the bottom. It would still be the same tree.
Here's how I got to 9:
a) We're looking for all trees with total nodes = 10 and no nodes of degree 2. They can either be 1 or >=3.
b) The solutions will have n leaf nodes (of degree 1) and k interior nodes of degree >=3, where n+k = 10.
c) In the degenerate solution of a single interior node and 9 leaves, the single interior node has degree 9.
d) In every other solution with multiple interior nodes, there is at least one edge connecting two interior nodes.
e) The sum of the degrees of the interior nodes double-counts all the shared edges between two interior nodes. Therefore, the sum of the interior node degrees for the (sole) solution with one interior node is 9, the sum of the degrees for solutions with two interior nodes is 10, three interior nodes is 11, etc.
f) Therefore, the problem is sort of related to the number of n-sized compositions of each sum:
1) For a single interior node, the sum is 9 and the single solution is 9
2) For two interior nodes, the sum is 10 and the 2-sized solutions (with minimum degree 3) are 7,3; 6,4; and 5,5
3) For three interior nodes, the sum is 11 and the 3-sized solutions are 3,3,5; 3,4,4; 3,5,3; 4,3,4. The example I posted in my last question was a tree with interior node degrees of 3,5,3. My question was whether the order of the edges coming from those nodes matters; in many data structures and algorithms it does. Here I'm going by your instruction that it doesn't.
4) For four interior nodes, the sum is 12 and the only 4-sized solution is 3,3,3,3.
Anything greater than four interior nodes can't satisfy the condition that all interior nodes have degree >=3 with only 10 total nodes, so 4 is the biggest (or most "spread out") tree that can work.
But that's only 9 distinct trees, I don't know what the last one is. I'm sure I'm missing something obvious though...
Quote: beachbumbabsFWIW, as I understand it, your example is the same in both iterations, or equivalent. I could be wrong.
Can you elaborate on that? Are you referring to my four example for the n=8 case? If so, which two do you accuse of being equivalent?
Quote:I don't have a graphic.
Can I trouble you to make the diagrams in Paint and then upload them to any file-sharing site?
The trick for me was to realize that there are multiple orientations of four interior nodes, something that didn't come through when I was writing them down just using numbers. The moral of the story: data representation is everything.
For what it's worth, there's no chance this actually took anyone two years.
Quote: MathExtremistNever mind, I got them all:
Indeed you did. Congratulations!
Can you elaborate on the "four interior nodes"? I'd like to make an Ask the Wizard question out of this and it would be nice to explain how to arrive at the answer without trial and error.
Quote: WizardCan you elaborate on that? Are you referring to my four example for the n=8 case? If so, which two do you accuse of being equivalent?
I was replying to ME, not to you. Yours were good. He had an equivalence in his first post, and you and I answered him at the same time.
Quote:Can I trouble you to make the diagrams in Paint and then upload them to any file-sharing site?
ME has illustrated all three in the middle row of his complete answer, so it would be redundant now. I had the other nine, but can't honestly say I "saw" your original example, so I voted 9 in the poll. For me, your example was the only counter -intuitive one.
That's what could've made the solution so hard and spoke to Will's genius in the movie-- If I remember the movie, the professor doesn't volunteer the number of trees in the correct solution, so not only did Will have to draw the ten trees but he also had to prove that there are exactly ten and only ten trees in the answer. Drawing the ten trees even when you know there are ten trees is a challenge, but how do you prove that you've got 'em all?
Consider too that formulating an answer for any n is difficult even when you need it to be accurate for trees of size n small; for instance, the number of trees in the solution for size n=3 is zero, because any tree of size 3 would be either i) reducible (if it weren't a triangle) or ii) cyclical (if it were a triangle), both of which are disallowed.
If k were the total number of trees in the solution and n were the size of the trees, then (n,k) would be:
(0,0)
(1,1)
(2,1)
(3,0)
(4,1)
(5,1)
(6,2)
(7,2)
(8,4)
(9,5)
(10,10)
(11,14)
(12,26)
So in other words, what's the function that would generate the series:
(k sub n) = 0, 1, 1, 0, 1, 1, 2, 2, 4, 5, 10, 14, 26....
Quote: docbrock"What is the general answer for any n?"...
Thanks, good post. Welcome to the forum. I don't suppose you can provide a formula for the general case of n? Or prove there aren't more than 10 for n=10?
If there are three or fewer interior nodes, they have to be in a line (or just a dot). But four can start branching -- the two orientations are (a) all four in a line and (b) a T shape. You can't have five interior nodes for n=10 because there aren't enough edges left, but for some other n>10 you will, and with five interior nodes there are three ways to arrange them: a straight line, a big T, and a cross. So the number of solutions for n nodes is going to involve the ordered partition -- if that's the right phrase -- of (# edges + # interior nodes - 1) as well as the number of ways each # of interior nodes can be arranged. From what I've just researched, there's no straightforward formula for that:Quote: WizardIndeed you did. Congratulations!
Can you elaborate on the "four interior nodes"? I'd like to make an Ask the Wizard question out of this and it would be nice to explain how to arrive at the answer without trial and error.
http://oeis.org/A000014
Edit: I think my method of counting the interior degrees leads to a proof that there are no more than 10 solutions for n=10. For interior nodes k < 4, there is only one solution per partition and there are 8 of those. For the one partition with interior nodes k=4 (3,3,3,3), there are only two ways to arrange those. That totals 10. There can't be any others.
The professor in the movie did say that it took the faculty 'two years to prove' the problem, but from the looks of it Will just drew all the trees on the chalkboard; he didn't produce a proof that there were exactly 10 qualifying trees for n=10. So Will could've presumably just concluded that through intuition, if he were capable of that (just as it's intuitive that there are no solutions for n=3 or one solution for n=2), or through a more informal but still complete and valid argument.
The brief research I did also led me back to that same link and I agree, there doesn't seem to be any straightforward formula for any n.
If there isn't one though, I'd like to know how the 'tree counts' that make up the integer series listed on that link (for n=0 through n=39) were calculated, especially the larger ones as n gets closer to 39:
0, 1, 1, 0, 1, 1, 2, 2, 4, 5, 10, 14, 26, 42, 78, 132, 249, 445, 842, 1561, 2988, 5671, 10981, 21209, 41472, 81181, 160176, 316749, 629933, 1256070, 2515169, 5049816, 10172638, 20543579, 41602425, 84440886, 171794492, 350238175, 715497037, 1464407113
Obviously you can't draw or list every one of the 1464407113 qualifying trees for n=39.
Quote: docbrockI'd like to know how the 'tree counts' that make up the integer series listed on that link (for n=0 through n=39) were calculated, especially the larger ones as n gets closer to 39:
I'd assume via a computer algorithm. But at the point of n=39, it was breaking the computer's limits.
Quote: tringlomaneI'd assume via a computer algorithm.
Yep, I'd agree. But wouldn't you consider that algorithm to be a formula that could solve for any n? Or would there have to be different algorithms for different ns?
Nope, this work was done long before folks like us could whip out a quick simulation using a high level language on a commodity computer.Quote: tringlomaneI'd assume via a computer algorithm. But at the point of n=39, it was breaking the computer's limits.
See:
http://arxiv.org/pdf/math/0008145.pdf, p. 13, which not only references a 1959 paper by F. Harary and G. Prins on the topic (but which I can't immediately find on the Internet) but points out that a homeomorphically-irreducible tree is the dual of a dissected polygon, and therefore of a cluster of edge-adjacent regular polygons. That's pretty cool:

That means the question on the trees is equivalent to "how many non-equivalent polygon clusters are there that fulfill n = s - k + 2, where s = total number of sides in all polygons and k = total number of polygons." It also means my intuition on the numeric representation (from my post where I set out 9 trees) has a direct geometric analog. It's easy to see how the numeric representation 3,3,3,3 (that is, four triangles) has two unique clusters:

Of course, it means that numeric representation is insufficient and incomplete, but that's a refinement for a later point.
Could you just elaborate a little about how you came up with n = s - k + 2? Particularly, why you're subtracting the total of polygons and the logic behind adding 2, which presumably is a constant for all n?
http://math.unideb.hu/media/horvath-gabor/publications/gwh2.pdf
See section 5, starting at the bottom of p. 11.
I thought about it differently - consider the problem as a backbone of major roads joining a number of towns and then where each town has some minor road dead-ends. If the town is at the end of the major road it needs two minor road dead-ends, however a town in the middle could have only one minor road dead-end.
1 (i) No major road, one town has nine dead ends.
3 (ii) Major road connects two towns, this leaves 8 dead ends which can be (6-2) (5-3) or (4-4) - i.e. ways to have two integers adding up to 8 where both >=2..
4 (iii) Major road connects three towns. The major road must be A-B-C (as looping isn't allowed). This leaves
7 dead ends where the end towns must have >=2 and the middle >=1. (4-1-2) (3-1-3) (3-2-2) (2-3-2) - i.e. ways to have three integers adding up to 7 where a and c >=2, b >=1.
(iv) Major road connects four towns,
1 (a) Road goes A-B-C-D (i.e. all in long line). Similar logic shows total=6, so only solution is (2 1 1 2)
1 (b) Road goes A-B B-C B-D (i.e. the major road forms a "T" shape). The town in the middle doesn't need any minor roads (although for larger puzzles it could) and the other three are at the end of the road so nead >=2 minor roads. Only solution is A C and D have two minor roads each (2 0 2 2).
(v) Various methods of having major road connecting five towns uses up too many nodes to leave 2 for each end point - so no further solutions.
Hope this logic helps shows the proof. Here's my working with the 10th Eureka solution at the top!

Also, I noticed an interesting plot hole - when the professor chases Will away from the chalkboard and then confirms that Will's solution is true, there are only eight trees on the board - not the full ten.
Quote: docbrockAlso, I noticed an interesting plot hole - when the professor chases Will away from the chalkboard and then confirms that Will's solution is true, there are only eight trees on the board - not the full ten.
That's true. I mention this omission on my page of math problems, problem 220.
I was trying it and got 5 of them done. Then I was like, these do seem homeopathically nonreducible or whatever the lingo is, so I figured the 5 I'd done were all the same. I was thinking up a sixth one, and was like F this, these are probably all the same and I'm wasting my time. Then again I don't really know what half those words mean.
Then I google it and realize my first 5 were good and the sixth I was thinking up was there too! That makes me mad, because I see 2 more I know I would have figured out and two that I likely wouldn't have gotten unless I spent more time (and not writing it on the back of an old Palms mailer with a sharpie like the damn hobo that I am).
Edit: apparently i shouldn't post a pic that has my info n stuff on it. From this picture (top left, to right, then middle left to right, etc. numbered, I got:

Thinking of #1, & #2. I wrote out 3, 6, 7, 8, and 10.
1 being top left, 8 being the round ball, 10 being the last one. And 7 is directly above 10.
Lower one on far left I wouldn't have figured out without more time. The one on bottom row, to the left, I wouldn't have done because I'd have thought it was pathomagically unreducibale with #6.

Quote: WizardThat's true. I mention this omission on my page of math problems, problem 220.
I didn't know this site existed. I have a mathematician friend of mine that would love this -- I'll pass it along to him.
Quote: docbrockI didn't know this site existed. I have a mathematician friend of mine that would love this -- I'll pass it along to him.
Please do. That is my first web page. Wizard of Odds is actually a spin-off of it, because it originally had so many problems related to probability in casino games.


