Recommended online casinos

Thread Rating:

falecf4
falecf4
falecf4
  • Threads: 5
  • Posts: 37
Joined: Dec 7, 2014
June 22nd, 2015 at 1:14:04 PM permalink
Just want to make sure I am figuring this right. In baccarat given 8 consecutive hands I want to figure out how many different ways it can happen with ties being excluded. Is it simply the 8 hands to the power of possible outcomes per hand (8^2=64)?
"I'm not superstitious but I am a little stitious." -Michael Scott
ThatDonGuy
ThatDonGuy
ThatDonGuy
  • Threads: 122
  • Posts: 6679
Joined: Jun 22, 2011
June 22nd, 2015 at 1:16:10 PM permalink
Assuming I am reading this right, it is the other way around - the number of possible results raised to the power of the number of hands. In this case, 28 = 256.

I assume you mean something like:
WWWWWWWW
WWWWWWWL
WWWWWWLW
WWWWWWLL
WWWWWLWW
.....
LLLLLLWW
LLLLLLWL
LLLLLLLW
LLLLLLLL
falecf4
falecf4
falecf4
  • Threads: 5
  • Posts: 37
Joined: Dec 7, 2014
June 22nd, 2015 at 1:18:59 PM permalink
I prefer to read it as Player, Banker versus Win, Loss but same effect. Wow, 256 just seems high to me.
"I'm not superstitious but I am a little stitious." -Michael Scott
mustangsally
mustangsally
mustangsally
  • Threads: 25
  • Posts: 2463
Joined: Mar 29, 2011
June 22nd, 2015 at 2:17:56 PM permalink
Quote: falecf4

I prefer to read it as Player, Banker versus Win, Loss but same effect.

like this
B,B,B,B,B,B,B,B
B,B,B,B,B,B,B,P
B,B,B,B,B,B,P,B
B,B,B,B,B,B,P,P
B,B,B,B,B,P,B,B
B,B,B,B,B,P,B,P
B,B,B,B,B,P,P,B
B,B,B,B,B,P,P,P
B,B,B,B,P,B,B,B
B,B,B,B,P,B,B,P
B,B,B,B,P,B,P,B
B,B,B,B,P,B,P,P
B,B,B,B,P,P,B,B
B,B,B,B,P,P,B,P
B,B,B,B,P,P,P,B
B,B,B,B,P,P,P,P
B,B,B,P,B,B,B,B
B,B,B,P,B,B,B,P
B,B,B,P,B,B,P,B
B,B,B,P,B,B,P,P
B,B,B,P,B,P,B,B
B,B,B,P,B,P,B,P
B,B,B,P,B,P,P,B
B,B,B,P,B,P,P,P
B,B,B,P,P,B,B,B
B,B,B,P,P,B,B,P
B,B,B,P,P,B,P,B
B,B,B,P,P,B,P,P
B,B,B,P,P,P,B,B
B,B,B,P,P,P,B,P
B,B,B,P,P,P,P,B
B,B,B,P,P,P,P,P
B,B,P,B,B,B,B,B
B,B,P,B,B,B,B,P
B,B,P,B,B,B,P,B
B,B,P,B,B,B,P,P
B,B,P,B,B,P,B,B
B,B,P,B,B,P,B,P
B,B,P,B,B,P,P,B
B,B,P,B,B,P,P,P
B,B,P,B,P,B,B,B
B,B,P,B,P,B,B,P
B,B,P,B,P,B,P,B
B,B,P,B,P,B,P,P
B,B,P,B,P,P,B,B
B,B,P,B,P,P,B,P
B,B,P,B,P,P,P,B
B,B,P,B,P,P,P,P
B,B,P,P,B,B,B,B
B,B,P,P,B,B,B,P
B,B,P,P,B,B,P,B
B,B,P,P,B,B,P,P
B,B,P,P,B,P,B,B
B,B,P,P,B,P,B,P
B,B,P,P,B,P,P,B
B,B,P,P,B,P,P,P
B,B,P,P,P,B,B,B
B,B,P,P,P,B,B,P
B,B,P,P,P,B,P,B
B,B,P,P,P,B,P,P
B,B,P,P,P,P,B,B
B,B,P,P,P,P,B,P
B,B,P,P,P,P,P,B
B,B,P,P,P,P,P,P
B,P,B,B,B,B,B,B
B,P,B,B,B,B,B,P
B,P,B,B,B,B,P,B
B,P,B,B,B,B,P,P
B,P,B,B,B,P,B,B
B,P,B,B,B,P,B,P
B,P,B,B,B,P,P,B
B,P,B,B,B,P,P,P
B,P,B,B,P,B,B,B
B,P,B,B,P,B,B,P
B,P,B,B,P,B,P,B
B,P,B,B,P,B,P,P
B,P,B,B,P,P,B,B
B,P,B,B,P,P,B,P
B,P,B,B,P,P,P,B
B,P,B,B,P,P,P,P
B,P,B,P,B,B,B,B
B,P,B,P,B,B,B,P
B,P,B,P,B,B,P,B
B,P,B,P,B,B,P,P
B,P,B,P,B,P,B,B
B,P,B,P,B,P,B,P
B,P,B,P,B,P,P,B
B,P,B,P,B,P,P,P
B,P,B,P,P,B,B,B
B,P,B,P,P,B,B,P
B,P,B,P,P,B,P,B
B,P,B,P,P,B,P,P
B,P,B,P,P,P,B,B
B,P,B,P,P,P,B,P
B,P,B,P,P,P,P,B
B,P,B,P,P,P,P,P
B,P,P,B,B,B,B,B
B,P,P,B,B,B,B,P
B,P,P,B,B,B,P,B
B,P,P,B,B,B,P,P
B,P,P,B,B,P,B,B
B,P,P,B,B,P,B,P
B,P,P,B,B,P,P,B
B,P,P,B,B,P,P,P
B,P,P,B,P,B,B,B
B,P,P,B,P,B,B,P
B,P,P,B,P,B,P,B
B,P,P,B,P,B,P,P
B,P,P,B,P,P,B,B
B,P,P,B,P,P,B,P
B,P,P,B,P,P,P,B
B,P,P,B,P,P,P,P
B,P,P,P,B,B,B,B
B,P,P,P,B,B,B,P
B,P,P,P,B,B,P,B
B,P,P,P,B,B,P,P
B,P,P,P,B,P,B,B
B,P,P,P,B,P,B,P
B,P,P,P,B,P,P,B
B,P,P,P,B,P,P,P
B,P,P,P,P,B,B,B
B,P,P,P,P,B,B,P
B,P,P,P,P,B,P,B
B,P,P,P,P,B,P,P
B,P,P,P,P,P,B,B
B,P,P,P,P,P,B,P
B,P,P,P,P,P,P,B
B,P,P,P,P,P,P,P
P,B,B,B,B,B,B,B
P,B,B,B,B,B,B,P
P,B,B,B,B,B,P,B
P,B,B,B,B,B,P,P
P,B,B,B,B,P,B,B
P,B,B,B,B,P,B,P
P,B,B,B,B,P,P,B
P,B,B,B,B,P,P,P
P,B,B,B,P,B,B,B
P,B,B,B,P,B,B,P
P,B,B,B,P,B,P,B
P,B,B,B,P,B,P,P
P,B,B,B,P,P,B,B
P,B,B,B,P,P,B,P
P,B,B,B,P,P,P,B
P,B,B,B,P,P,P,P
P,B,B,P,B,B,B,B
P,B,B,P,B,B,B,P
P,B,B,P,B,B,P,B
P,B,B,P,B,B,P,P
P,B,B,P,B,P,B,B
P,B,B,P,B,P,B,P
P,B,B,P,B,P,P,B
P,B,B,P,B,P,P,P
P,B,B,P,P,B,B,B
P,B,B,P,P,B,B,P
P,B,B,P,P,B,P,B
P,B,B,P,P,B,P,P
P,B,B,P,P,P,B,B
P,B,B,P,P,P,B,P
P,B,B,P,P,P,P,B
P,B,B,P,P,P,P,P
P,B,P,B,B,B,B,B
P,B,P,B,B,B,B,P
P,B,P,B,B,B,P,B
P,B,P,B,B,B,P,P
P,B,P,B,B,P,B,B
P,B,P,B,B,P,B,P
P,B,P,B,B,P,P,B
P,B,P,B,B,P,P,P
P,B,P,B,P,B,B,B
P,B,P,B,P,B,B,P
P,B,P,B,P,B,P,B
P,B,P,B,P,B,P,P
P,B,P,B,P,P,B,B
P,B,P,B,P,P,B,P
P,B,P,B,P,P,P,B
P,B,P,B,P,P,P,P
P,B,P,P,B,B,B,B
P,B,P,P,B,B,B,P
P,B,P,P,B,B,P,B
P,B,P,P,B,B,P,P
P,B,P,P,B,P,B,B
P,B,P,P,B,P,B,P
P,B,P,P,B,P,P,B
P,B,P,P,B,P,P,P
P,B,P,P,P,B,B,B
P,B,P,P,P,B,B,P
P,B,P,P,P,B,P,B
P,B,P,P,P,B,P,P
P,B,P,P,P,P,B,B
P,B,P,P,P,P,B,P
P,B,P,P,P,P,P,B
P,B,P,P,P,P,P,P
P,P,B,B,B,B,B,B
P,P,B,B,B,B,B,P
P,P,B,B,B,B,P,B
P,P,B,B,B,B,P,P
P,P,B,B,B,P,B,B
P,P,B,B,B,P,B,P
P,P,B,B,B,P,P,B
P,P,B,B,B,P,P,P
P,P,B,B,P,B,B,B
P,P,B,B,P,B,B,P
P,P,B,B,P,B,P,B
P,P,B,B,P,B,P,P
P,P,B,B,P,P,B,B
P,P,B,B,P,P,B,P
P,P,B,B,P,P,P,B
P,P,B,B,P,P,P,P
P,P,B,P,B,B,B,B
P,P,B,P,B,B,B,P
P,P,B,P,B,B,P,B
P,P,B,P,B,B,P,P
P,P,B,P,B,P,B,B
P,P,B,P,B,P,B,P
P,P,B,P,B,P,P,B
P,P,B,P,B,P,P,P
P,P,B,P,P,B,B,B
P,P,B,P,P,B,B,P
P,P,B,P,P,B,P,B
P,P,B,P,P,B,P,P
P,P,B,P,P,P,B,B
P,P,B,P,P,P,B,P
P,P,B,P,P,P,P,B
P,P,B,P,P,P,P,P
P,P,P,B,B,B,B,B
P,P,P,B,B,B,B,P
P,P,P,B,B,B,P,B
P,P,P,B,B,B,P,P
P,P,P,B,B,P,B,B
P,P,P,B,B,P,B,P
P,P,P,B,B,P,P,B
P,P,P,B,B,P,P,P
P,P,P,B,P,B,B,B
P,P,P,B,P,B,B,P
P,P,P,B,P,B,P,B
P,P,P,B,P,B,P,P
P,P,P,B,P,P,B,B
P,P,P,B,P,P,B,P
P,P,P,B,P,P,P,B
P,P,P,B,P,P,P,P
P,P,P,P,B,B,B,B
P,P,P,P,B,B,B,P
P,P,P,P,B,B,P,B
P,P,P,P,B,B,P,P
P,P,P,P,B,P,B,B
P,P,P,P,B,P,B,P
P,P,P,P,B,P,P,B
P,P,P,P,B,P,P,P
P,P,P,P,P,B,B,B
P,P,P,P,P,B,B,P
P,P,P,P,P,B,P,B
P,P,P,P,P,B,P,P
P,P,P,P,P,P,B,B
P,P,P,P,P,P,B,P
P,P,P,P,P,P,P,B
P,P,P,P,P,P,P,P
Quote: falecf4

Wow, 256 just seems high to me.

i say start with round 1
only B or P are possible
from that round we can now have BP or BB or PB or PP after 2 rounds
each round possible outcomes has 2 possible outcomes for the next round (it goes round and round)
2*2 = 4 after 2 rounds

3 rounds = 2*2*2

looks something like this Tree (2 outcomes - 3 rounds)
follow the arrows from 0

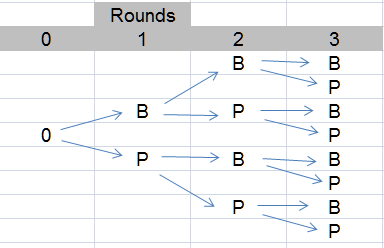
to 8 rounds = 2*2*2*2*2*2*2*2

counting Ties
we then have 3 * 3 after 2 rounds
3*3*3 after 3 rounds
3^8 = 6,561 possible sequences

==================================
and they (each possible sequence) are not all equal probable like in a fair coin toss

for example (with the probability of a B or P being constant)

B,B,B,B,B,B,B,B (sequence#1) has the highest probability of happening
and
P,P,P,P,P,P,P,P (sequence#256) has the lowest

now that seems and feels not right to me
at first thought

Sally
I Heart Vi Hart
MangoJ
MangoJ
MangoJ
  • Threads: 10
  • Posts: 905
Joined: Mar 12, 2011
June 22nd, 2015 at 2:38:39 PM permalink
Quote: falecf4

Just want to make sure I am figuring this right. In baccarat given 8 consecutive hands I want to figure out how many different ways it can happen with ties being excluded. Is it simply the 8 hands to the power of possible outcomes per hand (8^2=64)?



It's more like 2^8.
falecf4
falecf4
falecf4
  • Threads: 5
  • Posts: 37
Joined: Dec 7, 2014
June 22nd, 2015 at 8:56:02 PM permalink
Quote: mustangsally

like this

B,B,B,B,B,B,B,B
B,B,B,B,B,B,B,P
B,B,B,B,B,B,P,B
B,B,B,B,B,B,P,P
B,B,B,B,B,P,B,B
B,B,B,B,B,P,B,P
B,B,B,B,B,P,P,B
B,B,B,B,B,P,P,P
B,B,B,B,P,B,B,B
B,B,B,B,P,B,B,P
B,B,B,B,P,B,P,B
B,B,B,B,P,B,P,P
B,B,B,B,P,P,B,B
B,B,B,B,P,P,B,P
B,B,B,B,P,P,P,B
B,B,B,B,P,P,P,P
B,B,B,P,B,B,B,B
B,B,B,P,B,B,B,P
B,B,B,P,B,B,P,B
B,B,B,P,B,B,P,P
B,B,B,P,B,P,B,B
B,B,B,P,B,P,B,P
B,B,B,P,B,P,P,B
B,B,B,P,B,P,P,P
B,B,B,P,P,B,B,B
B,B,B,P,P,B,B,P
B,B,B,P,P,B,P,B
B,B,B,P,P,B,P,P
B,B,B,P,P,P,B,B
B,B,B,P,P,P,B,P
B,B,B,P,P,P,P,B
B,B,B,P,P,P,P,P
B,B,P,B,B,B,B,B
B,B,P,B,B,B,B,P
B,B,P,B,B,B,P,B
B,B,P,B,B,B,P,P
B,B,P,B,B,P,B,B
B,B,P,B,B,P,B,P
B,B,P,B,B,P,P,B
B,B,P,B,B,P,P,P
B,B,P,B,P,B,B,B
B,B,P,B,P,B,B,P
B,B,P,B,P,B,P,B
B,B,P,B,P,B,P,P
B,B,P,B,P,P,B,B
B,B,P,B,P,P,B,P
B,B,P,B,P,P,P,B
B,B,P,B,P,P,P,P
B,B,P,P,B,B,B,B
B,B,P,P,B,B,B,P
B,B,P,P,B,B,P,B
B,B,P,P,B,B,P,P
B,B,P,P,B,P,B,B
B,B,P,P,B,P,B,P
B,B,P,P,B,P,P,B
B,B,P,P,B,P,P,P
B,B,P,P,P,B,B,B
B,B,P,P,P,B,B,P
B,B,P,P,P,B,P,B
B,B,P,P,P,B,P,P
B,B,P,P,P,P,B,B
B,B,P,P,P,P,B,P
B,B,P,P,P,P,P,B
B,B,P,P,P,P,P,P
B,P,B,B,B,B,B,B
B,P,B,B,B,B,B,P
B,P,B,B,B,B,P,B
B,P,B,B,B,B,P,P
B,P,B,B,B,P,B,B
B,P,B,B,B,P,B,P
B,P,B,B,B,P,P,B
B,P,B,B,B,P,P,P
B,P,B,B,P,B,B,B
B,P,B,B,P,B,B,P
B,P,B,B,P,B,P,B
B,P,B,B,P,B,P,P
B,P,B,B,P,P,B,B
B,P,B,B,P,P,B,P
B,P,B,B,P,P,P,B
B,P,B,B,P,P,P,P
B,P,B,P,B,B,B,B
B,P,B,P,B,B,B,P
B,P,B,P,B,B,P,B
B,P,B,P,B,B,P,P
B,P,B,P,B,P,B,B
B,P,B,P,B,P,B,P
B,P,B,P,B,P,P,B
B,P,B,P,B,P,P,P
B,P,B,P,P,B,B,B
B,P,B,P,P,B,B,P
B,P,B,P,P,B,P,B
B,P,B,P,P,B,P,P
B,P,B,P,P,P,B,B
B,P,B,P,P,P,B,P
B,P,B,P,P,P,P,B
B,P,B,P,P,P,P,P
B,P,P,B,B,B,B,B
B,P,P,B,B,B,B,P
B,P,P,B,B,B,P,B
B,P,P,B,B,B,P,P
B,P,P,B,B,P,B,B
B,P,P,B,B,P,B,P
B,P,P,B,B,P,P,B
B,P,P,B,B,P,P,P
B,P,P,B,P,B,B,B
B,P,P,B,P,B,B,P
B,P,P,B,P,B,P,B
B,P,P,B,P,B,P,P
B,P,P,B,P,P,B,B
B,P,P,B,P,P,B,P
B,P,P,B,P,P,P,B
B,P,P,B,P,P,P,P
B,P,P,P,B,B,B,B
B,P,P,P,B,B,B,P
B,P,P,P,B,B,P,B
B,P,P,P,B,B,P,P
B,P,P,P,B,P,B,B
B,P,P,P,B,P,B,P
B,P,P,P,B,P,P,B
B,P,P,P,B,P,P,P
B,P,P,P,P,B,B,B
B,P,P,P,P,B,B,P
B,P,P,P,P,B,P,B
B,P,P,P,P,B,P,P
B,P,P,P,P,P,B,B
B,P,P,P,P,P,B,P
B,P,P,P,P,P,P,B
B,P,P,P,P,P,P,P
P,B,B,B,B,B,B,B
P,B,B,B,B,B,B,P
P,B,B,B,B,B,P,B
P,B,B,B,B,B,P,P
P,B,B,B,B,P,B,B
P,B,B,B,B,P,B,P
P,B,B,B,B,P,P,B
P,B,B,B,B,P,P,P
P,B,B,B,P,B,B,B
P,B,B,B,P,B,B,P
P,B,B,B,P,B,P,B
P,B,B,B,P,B,P,P
P,B,B,B,P,P,B,B
P,B,B,B,P,P,B,P
P,B,B,B,P,P,P,B
P,B,B,B,P,P,P,P
P,B,B,P,B,B,B,B
P,B,B,P,B,B,B,P
P,B,B,P,B,B,P,B
P,B,B,P,B,B,P,P
P,B,B,P,B,P,B,B
P,B,B,P,B,P,B,P
P,B,B,P,B,P,P,B
P,B,B,P,B,P,P,P
P,B,B,P,P,B,B,B
P,B,B,P,P,B,B,P
P,B,B,P,P,B,P,B
P,B,B,P,P,B,P,P
P,B,B,P,P,P,B,B
P,B,B,P,P,P,B,P
P,B,B,P,P,P,P,B
P,B,B,P,P,P,P,P
P,B,P,B,B,B,B,B
P,B,P,B,B,B,B,P
P,B,P,B,B,B,P,B
P,B,P,B,B,B,P,P
P,B,P,B,B,P,B,B
P,B,P,B,B,P,B,P
P,B,P,B,B,P,P,B
P,B,P,B,B,P,P,P
P,B,P,B,P,B,B,B
P,B,P,B,P,B,B,P
P,B,P,B,P,B,P,B
P,B,P,B,P,B,P,P
P,B,P,B,P,P,B,B
P,B,P,B,P,P,B,P
P,B,P,B,P,P,P,B
P,B,P,B,P,P,P,P
P,B,P,P,B,B,B,B
P,B,P,P,B,B,B,P
P,B,P,P,B,B,P,B
P,B,P,P,B,B,P,P
P,B,P,P,B,P,B,B
P,B,P,P,B,P,B,P
P,B,P,P,B,P,P,B
P,B,P,P,B,P,P,P
P,B,P,P,P,B,B,B
P,B,P,P,P,B,B,P
P,B,P,P,P,B,P,B
P,B,P,P,P,B,P,P
P,B,P,P,P,P,B,B
P,B,P,P,P,P,B,P
P,B,P,P,P,P,P,B
P,B,P,P,P,P,P,P
P,P,B,B,B,B,B,B
P,P,B,B,B,B,B,P
P,P,B,B,B,B,P,B
P,P,B,B,B,B,P,P
P,P,B,B,B,P,B,B
P,P,B,B,B,P,B,P
P,P,B,B,B,P,P,B
P,P,B,B,B,P,P,P
P,P,B,B,P,B,B,B
P,P,B,B,P,B,B,P
P,P,B,B,P,B,P,B
P,P,B,B,P,B,P,P
P,P,B,B,P,P,B,B
P,P,B,B,P,P,B,P
P,P,B,B,P,P,P,B
P,P,B,B,P,P,P,P
P,P,B,P,B,B,B,B
P,P,B,P,B,B,B,P
P,P,B,P,B,B,P,B
P,P,B,P,B,B,P,P
P,P,B,P,B,P,B,B
P,P,B,P,B,P,B,P
P,P,B,P,B,P,P,B
P,P,B,P,B,P,P,P
P,P,B,P,P,B,B,B
P,P,B,P,P,B,B,P
P,P,B,P,P,B,P,B
P,P,B,P,P,B,P,P
P,P,B,P,P,P,B,B
P,P,B,P,P,P,B,P
P,P,B,P,P,P,P,B
P,P,B,P,P,P,P,P
P,P,P,B,B,B,B,B
P,P,P,B,B,B,B,P
P,P,P,B,B,B,P,B
P,P,P,B,B,B,P,P
P,P,P,B,B,P,B,B
P,P,P,B,B,P,B,P
P,P,P,B,B,P,P,B
P,P,P,B,B,P,P,P
P,P,P,B,P,B,B,B
P,P,P,B,P,B,B,P
P,P,P,B,P,B,P,B
P,P,P,B,P,B,P,P
P,P,P,B,P,P,B,B
P,P,P,B,P,P,B,P
P,P,P,B,P,P,P,B
P,P,P,B,P,P,P,P
P,P,P,P,B,B,B,B
P,P,P,P,B,B,B,P
P,P,P,P,B,B,P,B
P,P,P,P,B,B,P,P
P,P,P,P,B,P,B,B
P,P,P,P,B,P,B,P
P,P,P,P,B,P,P,B
P,P,P,P,B,P,P,P
P,P,P,P,P,B,B,B
P,P,P,P,P,B,B,P
P,P,P,P,P,B,P,B
P,P,P,P,P,B,P,P
P,P,P,P,P,P,B,B
P,P,P,P,P,P,B,P
P,P,P,P,P,P,P,B
P,P,P,P,P,P,P,P
i say start with round 1
only B or P are possible
from that round we can now have BP or BB or PB or PP after 2 rounds
each round possible outcomes has 2 possible outcomes for the next round (it goes round and round)
2*2 = 4 after 2 rounds

3 rounds = 2*2*2

looks something like this Tree (2 outcomes - 3 rounds)
follow the arrows from 0

to 8 rounds = 2*2*2*2*2*2*2*2

counting Ties
we then have 3 * 3 after 2 rounds
3*3*3 after 3 rounds
3^8 = 6,561 possible sequences

==================================
and they (each possible sequence) are not all equal probable like in a fair coin toss

for example (with the probability of a B or P being constant)

B,B,B,B,B,B,B,B (sequence#1) has the highest probability of happening
and
P,P,P,P,P,P,P,P (sequence#256) has the lowest

now that seems and feels not right to me
at first thought

Sally



Thank you Sally this helps! Glad you brought up the probability also. Banker has a slightly higher probability of occurring than Player so the gap must widen when we look at the probability of a run of 8 for either and the gap is filled in by all of the other probabilities. Now does this make other sequences equal, such as B,P,P,P,P,P,P,P and P,P,B,P,P,P,P,P or would the probability of a sequence only be equal if the "streaks" within the sequence are equal B,B,P,B,B,B,B,B and B,B,B,B,B,P,B,B where they both have a streak of 2 and a streak of 5?
"I'm not superstitious but I am a little stitious." -Michael Scott
Twirdman
Twirdman
Twirdman
  • Threads: 0
  • Posts: 1004
Joined: Jun 5, 2013
June 22nd, 2015 at 10:45:56 PM permalink
Quote: falecf4

Quote: mustangsally

like this

B,B,B,B,B,B,B,B
B,B,B,B,B,B,B,P
B,B,B,B,B,B,P,B
B,B,B,B,B,B,P,P
B,B,B,B,B,P,B,B
B,B,B,B,B,P,B,P
B,B,B,B,B,P,P,B
B,B,B,B,B,P,P,P
B,B,B,B,P,B,B,B
B,B,B,B,P,B,B,P
B,B,B,B,P,B,P,B
B,B,B,B,P,B,P,P
B,B,B,B,P,P,B,B
B,B,B,B,P,P,B,P
B,B,B,B,P,P,P,B
B,B,B,B,P,P,P,P
B,B,B,P,B,B,B,B
B,B,B,P,B,B,B,P
B,B,B,P,B,B,P,B
B,B,B,P,B,B,P,P
B,B,B,P,B,P,B,B
B,B,B,P,B,P,B,P
B,B,B,P,B,P,P,B
B,B,B,P,B,P,P,P
B,B,B,P,P,B,B,B
B,B,B,P,P,B,B,P
B,B,B,P,P,B,P,B
B,B,B,P,P,B,P,P
B,B,B,P,P,P,B,B
B,B,B,P,P,P,B,P
B,B,B,P,P,P,P,B
B,B,B,P,P,P,P,P
B,B,P,B,B,B,B,B
B,B,P,B,B,B,B,P
B,B,P,B,B,B,P,B
B,B,P,B,B,B,P,P
B,B,P,B,B,P,B,B
B,B,P,B,B,P,B,P
B,B,P,B,B,P,P,B
B,B,P,B,B,P,P,P
B,B,P,B,P,B,B,B
B,B,P,B,P,B,B,P
B,B,P,B,P,B,P,B
B,B,P,B,P,B,P,P
B,B,P,B,P,P,B,B
B,B,P,B,P,P,B,P
B,B,P,B,P,P,P,B
B,B,P,B,P,P,P,P
B,B,P,P,B,B,B,B
B,B,P,P,B,B,B,P
B,B,P,P,B,B,P,B
B,B,P,P,B,B,P,P
B,B,P,P,B,P,B,B
B,B,P,P,B,P,B,P
B,B,P,P,B,P,P,B
B,B,P,P,B,P,P,P
B,B,P,P,P,B,B,B
B,B,P,P,P,B,B,P
B,B,P,P,P,B,P,B
B,B,P,P,P,B,P,P
B,B,P,P,P,P,B,B
B,B,P,P,P,P,B,P
B,B,P,P,P,P,P,B
B,B,P,P,P,P,P,P
B,P,B,B,B,B,B,B
B,P,B,B,B,B,B,P
B,P,B,B,B,B,P,B
B,P,B,B,B,B,P,P
B,P,B,B,B,P,B,B
B,P,B,B,B,P,B,P
B,P,B,B,B,P,P,B
B,P,B,B,B,P,P,P
B,P,B,B,P,B,B,B
B,P,B,B,P,B,B,P
B,P,B,B,P,B,P,B
B,P,B,B,P,B,P,P
B,P,B,B,P,P,B,B
B,P,B,B,P,P,B,P
B,P,B,B,P,P,P,B
B,P,B,B,P,P,P,P
B,P,B,P,B,B,B,B
B,P,B,P,B,B,B,P
B,P,B,P,B,B,P,B
B,P,B,P,B,B,P,P
B,P,B,P,B,P,B,B
B,P,B,P,B,P,B,P
B,P,B,P,B,P,P,B
B,P,B,P,B,P,P,P
B,P,B,P,P,B,B,B
B,P,B,P,P,B,B,P
B,P,B,P,P,B,P,B
B,P,B,P,P,B,P,P
B,P,B,P,P,P,B,B
B,P,B,P,P,P,B,P
B,P,B,P,P,P,P,B
B,P,B,P,P,P,P,P
B,P,P,B,B,B,B,B
B,P,P,B,B,B,B,P
B,P,P,B,B,B,P,B
B,P,P,B,B,B,P,P
B,P,P,B,B,P,B,B
B,P,P,B,B,P,B,P
B,P,P,B,B,P,P,B
B,P,P,B,B,P,P,P
B,P,P,B,P,B,B,B
B,P,P,B,P,B,B,P
B,P,P,B,P,B,P,B
B,P,P,B,P,B,P,P
B,P,P,B,P,P,B,B
B,P,P,B,P,P,B,P
B,P,P,B,P,P,P,B
B,P,P,B,P,P,P,P
B,P,P,P,B,B,B,B
B,P,P,P,B,B,B,P
B,P,P,P,B,B,P,B
B,P,P,P,B,B,P,P
B,P,P,P,B,P,B,B
B,P,P,P,B,P,B,P
B,P,P,P,B,P,P,B
B,P,P,P,B,P,P,P
B,P,P,P,P,B,B,B
B,P,P,P,P,B,B,P
B,P,P,P,P,B,P,B
B,P,P,P,P,B,P,P
B,P,P,P,P,P,B,B
B,P,P,P,P,P,B,P
B,P,P,P,P,P,P,B
B,P,P,P,P,P,P,P
P,B,B,B,B,B,B,B
P,B,B,B,B,B,B,P
P,B,B,B,B,B,P,B
P,B,B,B,B,B,P,P
P,B,B,B,B,P,B,B
P,B,B,B,B,P,B,P
P,B,B,B,B,P,P,B
P,B,B,B,B,P,P,P
P,B,B,B,P,B,B,B
P,B,B,B,P,B,B,P
P,B,B,B,P,B,P,B
P,B,B,B,P,B,P,P
P,B,B,B,P,P,B,B
P,B,B,B,P,P,B,P
P,B,B,B,P,P,P,B
P,B,B,B,P,P,P,P
P,B,B,P,B,B,B,B
P,B,B,P,B,B,B,P
P,B,B,P,B,B,P,B
P,B,B,P,B,B,P,P
P,B,B,P,B,P,B,B
P,B,B,P,B,P,B,P
P,B,B,P,B,P,P,B
P,B,B,P,B,P,P,P
P,B,B,P,P,B,B,B
P,B,B,P,P,B,B,P
P,B,B,P,P,B,P,B
P,B,B,P,P,B,P,P
P,B,B,P,P,P,B,B
P,B,B,P,P,P,B,P
P,B,B,P,P,P,P,B
P,B,B,P,P,P,P,P
P,B,P,B,B,B,B,B
P,B,P,B,B,B,B,P
P,B,P,B,B,B,P,B
P,B,P,B,B,B,P,P
P,B,P,B,B,P,B,B
P,B,P,B,B,P,B,P
P,B,P,B,B,P,P,B
P,B,P,B,B,P,P,P
P,B,P,B,P,B,B,B
P,B,P,B,P,B,B,P
P,B,P,B,P,B,P,B
P,B,P,B,P,B,P,P
P,B,P,B,P,P,B,B
P,B,P,B,P,P,B,P
P,B,P,B,P,P,P,B
P,B,P,B,P,P,P,P
P,B,P,P,B,B,B,B
P,B,P,P,B,B,B,P
P,B,P,P,B,B,P,B
P,B,P,P,B,B,P,P
P,B,P,P,B,P,B,B
P,B,P,P,B,P,B,P
P,B,P,P,B,P,P,B
P,B,P,P,B,P,P,P
P,B,P,P,P,B,B,B
P,B,P,P,P,B,B,P
P,B,P,P,P,B,P,B
P,B,P,P,P,B,P,P
P,B,P,P,P,P,B,B
P,B,P,P,P,P,B,P
P,B,P,P,P,P,P,B
P,B,P,P,P,P,P,P
P,P,B,B,B,B,B,B
P,P,B,B,B,B,B,P
P,P,B,B,B,B,P,B
P,P,B,B,B,B,P,P
P,P,B,B,B,P,B,B
P,P,B,B,B,P,B,P
P,P,B,B,B,P,P,B
P,P,B,B,B,P,P,P
P,P,B,B,P,B,B,B
P,P,B,B,P,B,B,P
P,P,B,B,P,B,P,B
P,P,B,B,P,B,P,P
P,P,B,B,P,P,B,B
P,P,B,B,P,P,B,P
P,P,B,B,P,P,P,B
P,P,B,B,P,P,P,P
P,P,B,P,B,B,B,B
P,P,B,P,B,B,B,P
P,P,B,P,B,B,P,B
P,P,B,P,B,B,P,P
P,P,B,P,B,P,B,B
P,P,B,P,B,P,B,P
P,P,B,P,B,P,P,B
P,P,B,P,B,P,P,P
P,P,B,P,P,B,B,B
P,P,B,P,P,B,B,P
P,P,B,P,P,B,P,B
P,P,B,P,P,B,P,P
P,P,B,P,P,P,B,B
P,P,B,P,P,P,B,P
P,P,B,P,P,P,P,B
P,P,B,P,P,P,P,P
P,P,P,B,B,B,B,B
P,P,P,B,B,B,B,P
P,P,P,B,B,B,P,B
P,P,P,B,B,B,P,P
P,P,P,B,B,P,B,B
P,P,P,B,B,P,B,P
P,P,P,B,B,P,P,B
P,P,P,B,B,P,P,P
P,P,P,B,P,B,B,B
P,P,P,B,P,B,B,P
P,P,P,B,P,B,P,B
P,P,P,B,P,B,P,P
P,P,P,B,P,P,B,B
P,P,P,B,P,P,B,P
P,P,P,B,P,P,P,B
P,P,P,B,P,P,P,P
P,P,P,P,B,B,B,B
P,P,P,P,B,B,B,P
P,P,P,P,B,B,P,B
P,P,P,P,B,B,P,P
P,P,P,P,B,P,B,B
P,P,P,P,B,P,B,P
P,P,P,P,B,P,P,B
P,P,P,P,B,P,P,P
P,P,P,P,P,B,B,B
P,P,P,P,P,B,B,P
P,P,P,P,P,B,P,B
P,P,P,P,P,B,P,P
P,P,P,P,P,P,B,B
P,P,P,P,P,P,B,P
P,P,P,P,P,P,P,B
P,P,P,P,P,P,P,P
i say start with round 1
only B or P are possible
from that round we can now have BP or BB or PB or PP after 2 rounds
each round possible outcomes has 2 possible outcomes for the next round (it goes round and round)
2*2 = 4 after 2 rounds

3 rounds = 2*2*2

looks something like this Tree (2 outcomes - 3 rounds)
follow the arrows from 0

to 8 rounds = 2*2*2*2*2*2*2*2

counting Ties
we then have 3 * 3 after 2 rounds
3*3*3 after 3 rounds
3^8 = 6,561 possible sequences

==================================
and they (each possible sequence) are not all equal probable like in a fair coin toss

for example (with the probability of a B or P being constant)

B,B,B,B,B,B,B,B (sequence#1) has the highest probability of happening
and
P,P,P,P,P,P,P,P (sequence#256) has the lowest

now that seems and feels not right to me
at first thought

Sally



Thank you Sally this helps! Glad you brought up the probability also. Banker has a slightly higher probability of occurring than Player so the gap must widen when we look at the probability of a run of 8 for either and the gap is filled in by all of the other probabilities. Now does this make other sequences equal, such as B,P,P,P,P,P,P,P and P,P,B,P,P,P,P,P or would the probability of a sequence only be equal if the "streaks" within the sequence are equal B,B,P,B,B,B,B,B and B,B,B,B,B,P,B,B where they both have a streak of 2 and a streak of 5?



The probabilities are equal as long as the number of players and number of bankers in both groups are the same.
falecf4
falecf4
falecf4
  • Threads: 5
  • Posts: 37
Joined: Dec 7, 2014
June 23rd, 2015 at 5:35:40 AM permalink
Quote: Twirdman

The probabilities are equal as long as the number of players and number of bankers in both groups are the same.



Thank you Twirdman! So a streak of all Player is least likely to occur and each time a Banker is added to the sequence the probability increases until there are all Bankers, being the most likely event.

Thank you for everyone's contribution! This information is very useful to me and, at the same time, worthless for a worthless betting system! 😉
"I'm not superstitious but I am a little stitious." -Michael Scott
charliepatrick
charliepatrick
charliepatrick
  • Threads: 39
  • Posts: 3011
Joined: Jun 17, 2011
June 23rd, 2015 at 7:46:30 AM permalink
Quote: falecf4

...for a worthless betting system! ...

Then it was worth asking the question. Answer: there is no good betting system when playing Baccarat!
teliot
teliot
teliot
  • Threads: 43
  • Posts: 2871
Joined: Oct 19, 2009
June 23rd, 2015 at 9:10:45 AM permalink
Quote: charliepatrick

there is no good betting system when playing Baccarat!

Optimal wagering in commission baccarat is to always wager on Banker. I am yet to observe a baccarat player who plays optimally.
Climate Casino: https://climatecasino.net/climate-casino/
Ibeatyouraces
Ibeatyouraces
Ibeatyouraces
  • Threads: 68
  • Posts: 11933
Joined: Jan 12, 2010
June 23rd, 2015 at 9:27:25 AM permalink
Quote: teliot

...I am yet to observe a baccarat player who plays optimally.


The optimal play is to not play at all.
DUHHIIIIIIIII HEARD THAT!
RSS Feed
  • Jump to: