please don't tell me some member solves it in 10 minutes.
I'm a builder. Just give me a bevel. ;-)
x=30
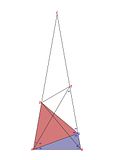
I got A, B, C, and D in relation to each other.
A being lower left of top triangle.
B being left angle of middle triangle.
C being bottom right of top triangle.
D being the unknown.
A + B = 130
C + D = 140
B + D = 110
A + C = 160
A = D + 20
B = C - 30
C = B + 30
D = A - 20
The top triangle is 20 [at the top], A at lower left, C at lower right.
Bottom triangle is 70 up top, 60 lower left and 50 lower right.
Left-most triangle is 50 up top, 110 at the right, 20 at bottom.
Right-most triangle is 40 up top, 110 at the left, and 30 at bottom.
Middle triangle is B at the left, 70 at the bottom, and D [the unknown] at the far right.
Using all the numbers/formula thingies I got....I wasn't able to "put them together" to figure out what D was equal to. But I feel like I was at least kinda close?
Or is my process way off?
:(
Beware [for those who care] -- the answer is posted a few posts down, in a not-spoiler-code-box-thing.
Hi RS,Quote: RSHow did you solve the answer?
I got A, B, C, and D in relation to each other.
A being lower left of top triangle.
B being left angle of middle triangle.
C being bottom right of top triangle.
D being the unknown.
A + B = 130
C + D = 140
B + D = 110
A + C = 160
A = D + 20
B = C - 30
C = B + 30
D = A - 20
The top triangle is 20 [at the top], A at lower left, C at lower right.
Bottom triangle is 70 up top, 60 lower left and 50 lower right.
Left-most triangle is 50 up top, 110 at the right, 20 at bottom.
Right-most triangle is 40 up top, 110 at the left, and 30 at bottom.
Middle triangle is B at the left, 70 at the bottom, and D [the unknown] at the far right.
Using all the numbers/formula thingies I got....I wasn't able to "put them together" to figure out what D was equal to. But I feel like I was at least kinda close?
Or is my process way off?
:(
I'm not there yet. Like you, I can get 4 simultaneous equations that only coexist with the correct answer, but struggling with the logic that solves them.
Quote: OnceDearHi RS,Quote: RSHow did you solve the answer?
I got A, B, C, and D in relation to each other.
A being lower left of top triangle.
B being left angle of middle triangle.
C being bottom right of top triangle.
D being the unknown.
A + B = 130
C + D = 140
B + D = 110
A + C = 160
A = D + 20
B = C - 30
C = B + 30
D = A - 20
The top triangle is 20 [at the top], A at lower left, C at lower right.
Bottom triangle is 70 up top, 60 lower left and 50 lower right.
Left-most triangle is 50 up top, 110 at the right, 20 at bottom.
Right-most triangle is 40 up top, 110 at the left, and 30 at bottom.
Middle triangle is B at the left, 70 at the bottom, and D [the unknown] at the far right.
Using all the numbers/formula thingies I got....I wasn't able to "put them together" to figure out what D was equal to. But I feel like I was at least kinda close?
Or is my process way off?
:(
I'm not there yet. Like you, I can get 4 simultaneous equations that only coexist with the correct answer, but struggling with the logic that solves them.
There are NOT 4 different equations !
sin(80)/sin(40)=sin(160-x)/sin(x)
x=30
Quote: ssho88Quote: OnceDearHi RS,Quote: RSHow did you solve the answer?
I got A, B, C, and D in relation to each other.
A being lower left of top triangle.
B being left angle of middle triangle.
C being bottom right of top triangle.
D being the unknown.
A + B = 130
C + D = 140
B + D = 110
A + C = 160
A = D + 20
B = C - 30
C = B + 30
D = A - 20
The top triangle is 20 [at the top], A at lower left, C at lower right.
Bottom triangle is 70 up top, 60 lower left and 50 lower right.
Left-most triangle is 50 up top, 110 at the right, 20 at bottom.
Right-most triangle is 40 up top, 110 at the left, and 30 at bottom.
Middle triangle is B at the left, 70 at the bottom, and D [the unknown] at the far right.
Using all the numbers/formula thingies I got....I wasn't able to "put them together" to figure out what D was equal to. But I feel like I was at least kinda close?
Or is my process way off?
:(
I'm not there yet. Like you, I can get 4 simultaneous equations that only coexist with the correct answer, but struggling with the logic that solves them.
There are NOT 4 different equations !
sin(80)/sin(40)=sin(160-x)/sin(x)
x=30
Help me out with that Ssho, please. Which bit of trig had I forgotten, bearing in mind we may not have any right angled triangles to work with.
Quote: OnceDearQuote: ssho88Quote: OnceDearHi RS,Quote: RSHow did you solve the answer?
I got A, B, C, and D in relation to each other.
A being lower left of top triangle.
B being left angle of middle triangle.
C being bottom right of top triangle.
D being the unknown.
A + B = 130
C + D = 140
B + D = 110
A + C = 160
A = D + 20
B = C - 30
C = B + 30
D = A - 20
The top triangle is 20 [at the top], A at lower left, C at lower right.
Bottom triangle is 70 up top, 60 lower left and 50 lower right.
Left-most triangle is 50 up top, 110 at the right, 20 at bottom.
Right-most triangle is 40 up top, 110 at the left, and 30 at bottom.
Middle triangle is B at the left, 70 at the bottom, and D [the unknown] at the far right.
Using all the numbers/formula thingies I got....I wasn't able to "put them together" to figure out what D was equal to. But I feel like I was at least kinda close?
Or is my process way off?
:(
I'm not there yet. Like you, I can get 4 simultaneous equations that only coexist with the correct answer, but struggling with the logic that solves them.
There are NOT 4 different equations !
sin(80)/sin(40)=sin(160-x)/sin(x)
x=30
Help me out with that Ssho, please. Which bit of trig had I forgotten, bearing in mind we may not have any right angled triangles to work with.
The above equation derived from 2 simultaneous equations. Just ask others to solve it, many people out there can do it !
Coined Here Source (Not Solution)
Hint. You need to draw more lines to arrive at a solution
Quote: RSHow did you come up with that equation, Ssho?
I can't upload the diagram. What is your email ?
solution in 6 steps It uses the properties of isosceles triangles, of which we need a few extra
Quote: OnceDearThis puzzle is a good find. A quick google revealed that it bears the name "Second-Hardest Easy Geometry Problem"
Coined Here Source (Not Solution)
Hint. You need to draw more lines to arrive at a solution
Really this is the "Second-Hardest Easy Geometry Problem" ?
And now I want to challenge people out there to solve this equation :-
sin(80)/sin(40)=sin(160-x)/sin(x)
.
.
.
tan(x) = sin(20)/[2*cos(40)-cos(20)]
.
.
.
.Anyone can solve it ?
[spoiler 30]
Quote: NYSithI came up with this by drawing it out on a post it note and doing the math.
Invisible math cannot be verified.
Invisible math cannot be disputed, either.
a(cos 80°) + b2 = c(cos 60°)
d(sin 50°) + b1 = e(sin 80°)
d(cos 50°) - b2 = e(cos 80°)
c(sin 60°) - e(sin 80°) = 0
c(cos 60°) + e(cos 80°) = 1
Six equations, six unknowns. That gave me the rise and run of the line above the angle, so drawing a straight line across, taking the arctangent, and using similar triangles gave me the same answer everyone else has. I think I might have made it a little harder than it had to be, especially when I realized what the length of the bottom part of the left leg was.
Quote: OnceDearI've now found a solution, not using Sin function at all.
solution in 6 steps It uses the properties of isosceles triangles, of which we need a few extra
I drew it out and figured out by imaging multiple triangles within the drawing. Since the sum of the angles of a triangle always equal 180 degrees, based on the given information, I was able to start filling in the missing angles. Once enough were filled in it became possible to solve it. Not sure how to post a picture of the post-it I did the work on, but it doesn't require any trig at all to solve.
Quote: MaxPenI solved it by looking at the picture. The ? Angle looked the same as the identified 30. I took two credit cards from my wallet and used them like a bevel to determine that the angles matched. Solved in less than 30 seconds. Took me more than 10 minutes to figure out how to do the spoiler tag though.
It's not drawn accurately... BUSTED.
Quote: NYSithI drew it out and figured out by imaging multiple triangles within the drawing. Since the sum of the angles of a triangle always equal 180 degrees, based on the given information, I was able to start filling in the missing angles. Once enough were filled in it became possible to solve it. Not sure how to post a picture of the post-it I did the work on, but it doesn't require any trig at all to solve.
Just for the hell of it, assume the answer is 20. Do all your missing angles work out?
Just for the hell of it, assume the answer is 40. Do all your missing angles work out?
We'll call the angle equaling 60 angle A
We'll call the angle equaling 50 angle B
At the intersection of the lines from those two angles we have an Apex we'll call angle C
Angle C has to equal 70 degrees since the sum of the angles of a triangle equal 180 degrees.
The intersection of the lines at Angel C form four distinct angles. The angle opposite angle C we'll call angle D has to be equal to angle C. I remember that there was a proof for that, but it's been 35 years or so, and I can't reference it. That will give us 140 degrees if we add Angle C and Angle D together. This intersection is also going to have something in common with a quadrilateral (square) the sum of the angles will equal 360 degrees so we can subtract 140 from 360 which gives us 220 degrees divided by two which will assign 110 degrees to those other angles. From there, we move back to the base of the overall puzzle. Since the sum of the angles at the base equal 160 degrees (20 + 60) and (50 + 30) at the very apex of the puzzle, that has to equal 20 degrees. At this point, there is enough information to walk this process through every angle and begin pulling smaller triangles within the overall puzzle and fill in the blanks.
Quote: NYSithNo...
So you got this far...

Keep going.
Quote: NYSithActually I got all the way through it, just didn't realize you wanted the breakdown all the way through. It's a lot of typing which isn't my best skill.
All you did was proclaim an answer. You didn't demonstrate it.
Quote: indignant99All you did was proclaim an answer. You didn't demonstrate it.
Ok, continuing on:
For some reason I subtracted 50 from the sum of angle A and B (130) to get my 80 degrees for Angle B. Not sure why I did that, but once I had Angle B at 80, I added it to the 70 inside the internal most triangle formed by the lines and assigned 30 degrees to Angle D. I added Angle D to the known angle next to it (40) and got 70 degrees. A straight line is a 180 degree angle so I subtracted the 70 degrees from 180 to get the 110 that is adjoined to them. At this point, I added 20 to the 110, then subtracted it from 180 to get 50 for Angle A on the diagram. May not make sense what I did, but I do stand by it and I still stand by my proclamation that the angle in question can't be 20 or 40 degrees without changing the given angles from the start of the puzzle.
Quote: indignant99It's not drawn accurately... BUSTED.
Ha....Just checked you are right. Looked close enough to me last night with 2 credit cards in hand. It's off by a few degrees. I got lucky. I make no claims of math prowess. The following graphic walks you through how I would find an answer from the info provided.

Can one of you math geniuses please go to the math section and explain my question about the 5 card double up feature please?
Quote: MaxPenHa....Just checked you are right. Looked close enough to me last night with 2 credit cards in hand. It's off by a few degrees. I got lucky. I make no claims of math prowess. The following graphic walks you through how I would find an answer from the info provided.
Can one of you math geniuses please go to the math section and explain my question about the 5 card double up feature please?
I'm still not following here. Particularly with step 10 and later. How'd you come up with 50, 80, 110, and 30?
Quote: RSQuote: MaxPenHa....Just checked you are right. Looked close enough to me last night with 2 credit cards in hand. It's off by a few degrees. I got lucky. I make no claims of math prowess. The following graphic walks you through how I would find an answer from the info provided.
Can one of you math geniuses please go to the math section and explain my question about the 5 card double up feature please?
I'm still not following here. Particularly with step 10 and later. How'd you come up with 50, 80, 110, and 30?
I think he used a try & error method ? Imagine what IF the answer x=29.51, how can he get it ?
Do you know what I mean?
I'm asking if you can assume that the top angle is 20, because that assumes that the lines don't change directions slightly at the intersections with the vertices of the inner triangle.
Same question about straight lines at the inner intersections.
Quote: Dalex64Is the outer shape a triangle, and can you assume that all lines at intersections continue at the same angle?
Do you know what I mean?
I'm asking if you can assume that the top angle is 20, because that assumes that the lines don't change directions slightly at the intersections with the vertices of the inner triangle.
Same question about straight lines at the inner intersections.
The outer shape is a triangle.
I don't think you can assume the lines continue the same way with the same angle on the opposite side. If this could be assumed, then you could find the answer in about 30 seconds.
Quote: ssho88Quote: RSQuote: MaxPenHa....Just checked you are right. Looked close enough to me last night with 2 credit cards in hand. It's off by a few degrees. I got lucky. I make no claims of math prowess. The following graphic walks you through how I would find an answer from the info provided.
Can one of you math geniuses please go to the math section and explain my question about the 5 card double up feature please?
I'm still not following here. Particularly with step 10 and later. How'd you come up with 50, 80, 110, and 30?
I think he used a try & error method ? Imagine what IF the answer x=29.51, how can he get it ?
X couldn't possibly equal 29.51 based on the given information at the start of this puzzle. (I do realize it says if in the statement) For that to be possible, the given angles would have to be changed, which changes the whole puzzle. The method I used which may have been poorly written, but makes sense is breaking the puzzle down into smaller triangles with the given information and filling in blanks as you work along. There is a point of guessing when you subtract 50 from 130 to derive 80 degrees for the innermost triangle. The straight line running from the base to the apex from the left side is 180 degrees, you have the 50 degree angle already. You have the 30 degree angle on the bottom right when combined with the apex of 20 at the very top then subtracted from 180 gives you the angle of 130 degrees. Subtracting the 50 from the 130 does give you 80, and you have to guess which one of the sub-angles it applies to in the puzzle. That's actually pretty easy since we know an 80 degree angle will look larger than a 50 degree angle. Just eyeballing the puzzle allows you to determine that the 80 degree angle is the one in between the two 50 degree angles. Once you have the 80 assigned plus the 70, once again its just a matter of subtracting 150 from 180 to get the missing 30 degree angle. Is this the correct way to solve the puzzle? I can't say for sure, but it worked for me.
My apologies for a convoluted drawn out answer. I hope it makes some sort of sense to anyone besides me.
However, given the if statement of 29.51, continuing the ifs, if the starting angles were adjusted to accommodate that as the answer, it might still be possible using my muddled reasoning to get the answer.
Quote: RSThe outer shape is a triangle.
I don't think you can assume the lines continue the same way with the same angle on the opposite side. If this could be assumed, then you could find the answer in about 30 seconds.
True statement, but with the given information, there is no reason to assume they aren't all straight lines. I went under the assumption that they were. I don't know what the original puzzle creator intended, so I just went with what I could see based on the visual. I would further assume that they have to be straight lines as they continue through the intersecting locations, because even a slight deviation would make the puzzle unsolvable even through the use of trig functions.
Quote: NYSithTrue statement, but with the given information, there is no reason to assume they aren't all straight lines. I went under the assumption that they were. I don't know what the original puzzle creator intended, so I just went with what I could see based on the visual. I would further assume that they have to be straight lines as they continue through the intersecting locations, because even a slight deviation would make the puzzle unsolvable even through the use of trig functions.
Had nothing to do with curvy or straight lines. It had to do with if the lines continue at the same angle when they hit another line. If you look at MaxPen's image, there are 4 green dots. The bottom right one connected with the middle left one creates an angle (50 degrees). If the line hits it and "bounces off" (like a ball thrown at a wall), then the opposite angle would also be 50 degrees. However, I don't think this is a valid assumption to be made, that the lines continue at the same angle after intersecting or touching another line.
Quote: RSHad nothing to do with curvy or straight lines. It had to do with if the lines continue at the same angle when they hit another line. If you look at MaxPen's image, there are 4 green dots. The bottom right one connected with the middle left one creates an angle (50 degrees). If the line hits it and "bounces off" (like a ball thrown at a wall), then the opposite angle would also be 50 degrees. However, I don't think this is a valid assumption to be made, that the lines continue at the same angle after intersecting or touching another line.
I agree with you, there is nothing supporting the assumptions. I just used some math I drudged up from high school geometry from about 35 years ago to work a few things out with the puzzle. Whatever voodoo I used worked for me and gave me the answer. I went back and looked at your process which is similar to the work I did on the post-it notes and in my head. Yours is a lot cleaner looking than mine though, you have a much better presentation.
(ii) Construct a 20-80-80 triangle (ABL) therefore AB=AL.
(iii) Draw DL and observe that AL=AD and angle LAD=60; therefore ADL is an equilateral triangle, so AD=DL=AL.
(iv) Observe that angle LAE = 60-20 = 40 and angle LEA = 40; therefore ALE is isosceles and EL=AL.
(v) Observe that angle DLE=40 (180-80-60) and DL=EL; therefore DLE is isosceles and angles DEL=LDE; because angle DLE=40, angle DEL=70 ((180-40)/2).
But DEL=40+x; so x=30.
Quote: NYSitha much better presentation.
Whose diagram? I presented one to RS - not the other way around.
Your arbitrary setting of angle A = 50, is a proclamation (without support, nor evidence, nor reasoning). You could set angle A to anything and have the others all work out.
Quote: RSI'm still not following here. Particularly with step 10 and later. How'd you come up with 50, 80, 110, and 30?
The P.O.O.M.A. method.
Quote: RSThe outer shape is a triangle.
I don't think you can assume the lines continue the same way with the same angle on the opposite side. If this could be assumed, then you could find the answer in about 30 seconds.
What? I really mean WHAT? Of course all the lines are straight. No bending at vertices. So, now that all the lines are straight, get the answer in 30 seconds.
Quote: indignant99Whose diagram? I presented one to RS - not the other way around.
Your arbitrary setting of angle A = 50, is a proclamation (without support, nor evidence, nor reasoning). You could set angle A to anything and have the others all work out.
That's a rather arbitrary conclusion about the no reasoning, of course there was reasoning, subtracting 50 degrees from 130 equals 80 degrees, obviously that would be assigned to the larger of the angles in the graphic depiction since the total compilation of angles are 50, 50, and 80. It takes reasoning to assign the largest angle to the largest of the two remaining options. You wouldn't wedge a square peg into a round hole if there was a square hole available. In any case, I came up with the correct answer with the correct values assigned to the angles throughout the puzzle. So, it really makes no difference at this point.
Quote: NYSithThat's a rather arbitrary conclusion about the no reasoning...
Of course you used reasoning after setting A = 50.
I want your reasoning, in the first place, that leads you to set A = 50.
Quote: indignant99Of course you used reasoning after setting A = 50.
I want your reasoning, in the first place, that leads you to set A = 50.
Is this Ashton Kutcher? I'm starting to think I'm on Punk'd. I stated the reasoning in the last post for assigning 50 to Angle A. On the left side of the diagram where we are able to ascertain the combination of Angle A + B = 130, I subtracted 50 from that total from the known angle which we will call Angle C. I made an assumption that whomever drew the original Puzzle diagram did so with an accurate depiction of the scale. Its obvious by visual inspection that one of the angles depicted between angle A and B is smaller than the others. With 80, I subtracted that as well from the 130 to give myself another 50 degrees. Using the visual inspection and reasoning, I assigned the values to the locations that made sense. Once those were plugged into the puzzle, it made it possible to figure out the remaining angles. Like I said, I'm using what I remember from 35 years ago and it worked. If this isn't a satisfactory answer, I'll have to bow out and await the next puzzle.
Quote: indignant99The P.O.O.M.A. method.
Draw a line from the lower left corner parallel to the line above the angle in question to form a trapezoid.
[20°+(60°-x)]+[x+40°]+[180°-(x+40°)]+[(180°-70°-x)+50°]=360° --> x=30°.
Quote: indignant99What? I really mean WHAT? Of course all the lines are straight. No bending at vertices. So, now that all the lines are straight, get the answer in 30 seconds.
Like I posted before, I'm not talking about if the lines are straight or curvy. Re-read the post I was responding to.
If the lines continue at the same angle when hitting the edge of the triangle (ie: it's reflection), then angle A is 50 (because the angle below it is 50). The rest is easy. B would be 80, C would be 110, and D would be 30 (the answer).
However, I don't think that is a fair assumption to make. Even if those are the correct answers, this wouldn't be the proper way to solve the problem.
Quote: RS(ie: it's reflection)...
This ain't a pool table. Construct the 20-degree angle. Then construct the 30-degree angle. Then connect the two intercept vertices. Your "no fair assumption" is correct.
Quote: NYSithIs this Ashton Kutcher?
No, that would be you. You arbitrarily set A=50. BZZZT, you're wrong.
Quote: indignant99No, that would be you. You arbitrarily set A=50. BZZZT, you're wrong.
hmmm...maybe guessing is not allowed. But, wrong? not exactly.
Quote: indignant99No, that would be you. You arbitrarily set A=50. BZZZT, you're wrong.
Actually I made the correct selection by placing 80 in Angle B and 50 in Angle A, you overlook the simple fact that a small triangle is formed by the 20 degree at the lower left of the puzzle. Angle B added to the Angle 50 that falls within the small triangle made up of 20 - 50 - 110 triangle at the lower left, will equal 130 degrees, adding 20 to the 130 gives you 150, subtract that from 180, it gives you 30 the answer to the puzzle. Therefore Angle A is not being set Arbitrarily to 50 because a change in the missing Angle equaling 30 would change the number of degrees set for the Angle set at 20 degrees. Placing the angles in this fashion allows for a proof that doesn't require any changes to the starting angles.