I guessing the Wizard himself can solve this one, but few if anyone else will get it [Dave's Conjecture]. Let's find out:
"You head the road construction department for a small county whose four towns are located at the corners of unit square one mile on each side.
Initially, no roads exist at all. You are commissioned to design a road network which need only "connect" all four towns. It needn't provide
an "efficient" route between any of them, only paved segments enabling traffic to reach any town from any other. Segments may be either curved
or straight, your choice. Your only option for paving costs 1 million dollars per mile, and your maximum budget is 2.75 million dollars. Describe your design."
P.S. Before you propose an "X" pattern, consider that its total distance is 2*sqrt(2) = 2.828, so that doesn't qualify.
Lotsa luck!
David C Blanchard (MIT '76)
dblanch256@gmail.com
http://demonstrations.wolfram.com/SteinerNetworksForFourPoints/
Let's say the four cities are at (0,0), (1,0), (1,1), and (0,1).
Let point A have coordinate [1/(sqrt(12),1/2].
Let point B have coordinate [1-(1/sqrt(12),1/2].
Make roads from (0,0) and (0,1) to A.
Make roads from (1,0) and (1,1) to B.
Make road from A to B.
Total distance = 4*sqrt(1/3) + 1 - 2*sqrt(1/12) = 2.732050808.
In other words, the road network will look like an H on a diet shape.
Quote: PerditionSpeaking of baiting what are the thoughts on the laundromat in Vegas called the Wizard of Suds?
How about Wizard of Sods lawn service?
Your only option for paving costs 1 million dollars per mile, and your maximum budget is 2.75 million dollars. Describe your design."
Build the road any way you like, and pave until you run out of money. The rest of the path is called 'Dirt Road'.
Quote: RaleighCrapsPennsylvania had the easy answer to this problem.
Your only option for paving costs 1 million dollars per mile, and your maximum budget is 2.75 million dollars. Describe your design."
Build the road any way you like, and pave until you run out of money. The rest of the path is called 'Dirt Road'.
Good thinking out of the box, but "any way you like" is not stated, "paved segments connecting" is. If non-paved segments were allowed as part of the solution I'd just blaze an "X" pattern path and take whats left of the 2.7 million to the casino!
Quote: BleedingChipsSlowly... I'd just blaze an "X" pattern path and take whats left of the 2.7 million to the casino!
I see you've worked for PENNDOT :)
Quote: FaceI see you've worked for PENNDOT :)
the reference is humorous now- but remember the Penn politician who blew his brains out at a press conference? - Budd Dwyer I think it was. That had to do with bribery and taking money from contract services.. was that related to PENNDOT or some other form of contracting?
Quote: Malaruthe reference is humorous now- but remember the Penn politician who blew his brains out at a press conference? - Budd Dwyer I think it was. That had to do with bribery and taking money from contract services.. was that related to PENNDOT or some other form of contracting?
PA does have a lot of dirt roads (much of the reason I like PA so much), and I always think than any gov run institution is corrupt at best and completely retarded at worst.
But as to your question, I've no idea. I was just making a joke with no basis in fact, sort of riding RaleighCraps coattails.
Quote: WizardGood problem!
Not only did Wiz come up with a solution he also came up with the optimum solution. I assume he assumed that the optimum shape would have equal angles between the roads. This is similar to the fact that a hexagon shape has the shortest lines possible to enclose an area that is filled with the fewest number of shapes.
6 Banks in a row
7 -8-9-10-11-12-13-14-15 Banks in a row could you see?
Quote: oz8324It's my first time here. How do I ask a question. For example on a 8 deck Baccarat. How many Bank runs of
6 Banks in a row
7 -8-9-10-11-12-13-14-15 Banks in a row could you see?
If you must ask that, and I hope you won't, please make a separate thread for it in the baccarat section.
That said, what's your answer (beyond "I think it has something to do with this ...")?
;)
I was hoping to award partial credit to anyone who could give at least a qualitative description, but The Wizard cast his spell before anyone else even had a
chance. I'm amused that some people simply posted a pointer to the Wizard's solution (probably without comprehending it) which amounts to saying "Yeah, what he said!" I guess that's a legitimate perk of being "The Wizard" and maybe I'm just a tiny bit jealous.
Anyway, for the rest of us, his solution (which exceeds the problem requirement by being optimal, not to mention irrational) looks something like this:
# #
###
# #
This figure contains 4 diagonal segments (from each corner) of equal length (A) due to symmetry, plus one horizontal "cross bar" (B) in the center. Lacking a symmetry argument for B, we must assume it may be a different length (B). Therefore the total roadwork distance (S) is given by S=4A+B.
Now, it's one thing to deduce the approximate shape (roughly speaking, it is a "morph" of an "H" with an "X" shape). It's a whole new level of difficulty to discover the values of A and B. [Hint: If your calculus is rusty, "I'd turn back, if I were you."]
OK, a few "last chances" to save face for the rest of you:
(1) What is "the other" solution? [I'm choosing my words very carefully here]
(2) In what way is the solution (either one) "counter-intuitive" with respect to the original problem?
(3) Why (in simple English) must the optimal solution contain (or not contain) any curved segments?
(4) Why (in simple English) does the optimal solution beat the more obvious "X" pattern? Putting it another way,
what is it about the "X" pattern that is "wasteful" relative to the optimal pattern?
COMING ATTRACTIONS: "Why "solve" a problem, if you can "design" the answer?"
I prefer to think of it as [1 + sqrt(3)] but I assume you chose the expanded form because it's easier to see it's components.
You were to modest to point out that your solution is actually optimal, but one of the readers did. I should thank him for that.
Are you a wizard-in-training yourself? ;)
Quote: dblanch256
(1) What is "the other" solution? [I'm choosing my words very carefully here]
(2) In what way is the solution (either one) "counter-intuitive" with respect to the original problem?
(3) Why (in simple English) must the optimal solution contain (or not contain) any curved segments?
(4) Why (in simple English) does the optimal solution beat the more obvious "X" pattern? Putting it another way,
what is it about the "X" pattern that is "wasteful" relative to the optimal pattern?
I surmise the other solution would be diagnol segments from the top and bottom corners with a vertical segment vs the optimal with a horizontal connection.
I don't exactly know why the answers would be counterintuitive besides that you stated they didn't need to be efficient which if one wanted to go from one town to the other that is connected via a side it would take more time than necessary. Also you didn't spend the entire 2.75 million so that may be cut out of future budgets, companies are always trying to save a buck. That and a traffic jam in the middle segment would be horrid at rush hour.
What is the quickest way between two points? A straight line. When trying to figure this problem out, I was racking my brain on how it could be done...I haven't done any sort of math in many years so I had to look a great deal up...first I thought of drawing a semi circle around the square but upon doing the math realized I would be way over budget, that and simply looking at the shapes I could have known that. I then decided that if I were to flip in the circle at two given corners I may be on to something an I with a parentheses on the top and bottom with the open ends facing away from connection with the I... But I realized this would also be not ideal because each curved segment would be longer than a mile. Upon this i deduced a triangle would better fit but I literally had no idea how to do the math for it and that is when I checked back here and saw something along those lines was posted. Oh well I tried.
Based on what I think the x pattern is relative because it allows the convergence of the two respective points from one side at an optimal rate but upon nearing the center it becomes wasteful having the extra distances connecting 4 points vs 2.
I may not by right...but I gave it the old college try...and honestly this problem really sparked my interest and was actually fun to try and deduce.
Quote: dblanch256Absolutely. Thank you so much for contributing that observation. It needed to be said, but I missed it.
Are you a wizard-in-training yourself? ;)
You may want to click on quote rather than reply so people know who you are talking to
Quote: 98ClubsI take note that this is not a "minimum" problem. using the spoiler below, about 1 square foot oughta do it in the center. Thanks for the $2.75million
Bisecting each side forms 4 small squares. The town-centers are in the center of each mini square but extend to the four corners. Thus each town exists at the four corners. Now an X pattern will consume less mileage than 2*SQRT(2) and less than 2.75 miles. Any leftover goes to local streets.
Clever, but you and I both know you "queered" the problem to suit your solution. ;)
Are you a wizard-in-training yourself? ;)
Quote: paisiello
Not only did Wiz come up with a solution he also came up with the optimum solution. I assume he assumed that the optimum shape would have equal angles between the roads. This is similar to the fact that a hexagon shape has the shortest lines possible to enclose an area that is filled with the fewest number of shapes.
Absolutely. Thank you so much for contributing that observation. It needed to be said, but I missed it.
Are you a wizard-in-training yourself? ;)
Quote: gameterrorI guess the correct solution is SteinerNetworks as explained here:
http://demonstrations.wolfram.com/SteinerNetworksForFourPoints/
Kudos, you've learned how to use Google.
That said, what's your answer (beyond "I think it has something to do with this ...")?
;)
Quote: TranscendQuote: dblanch256
(1) What is "the other" solution? [I'm choosing my words very carefully here]
(2) In what way is the solution (either one) "counter-intuitive" with respect to the original problem?
(3) Why (in simple English) must the optimal solution contain (or not contain) any curved segments?
(4) Why (in simple English) does the optimal solution beat the more obvious "X" pattern? Putting it another way,
what is it about the "X" pattern that is "wasteful" relative to the optimal pattern?
I surmise the other solution would be diagnol segments from the top and bottom corners with a vertical segment vs the optimal with a horizontal connection.
I don't exactly know why the answers would be counterintuitive besides that you stated they didn't need to be efficient which if one wanted to go from one town to the other that is connected via a side it would take more time than necessary. Also you didn't spend the entire 2.75 million so that may be cut out of future budgets, companies are always trying to save a buck. That and a traffic jam in the middle segment would be horrid at rush hour.
What is the quickest way between two points? A straight line. When trying to figure this problem out, I was racking my brain on how it could be done...I haven't done any sort of math in many years so I had to look a great deal up...first I thought of drawing a semi circle around the square but upon doing the math realized I would be way over budget, that and simply looking at the shapes I could have known that. I then decided that if I were to flip in the circle at two given corners I may be on to something an I with a parentheses on the top and bottom with the open ends facing away from connection with the I... But I realized this would also be not ideal because each curved segment would be longer than a mile. Upon this i deduced a triangle would better fit but I literally had no idea how to do the math for it and that is when I checked back here and saw something along those lines was posted. Oh well I tried.
Based on what I think the x pattern is relative because it allows the convergence of the two respective points from one side at an optimal rate but upon nearing the center it becomes wasteful having the extra distances connecting 4 points vs 2.
I may not by right...but I gave it the old college try...and honestly this problem really sparked my interest and was actually fun to try and deduce.
Bravo! Well played. Should I confirm what I believe you got right and let the rest of the class out early? I don't want to spoil it for the earnest folk who may still be contemplating suicide over it. I wish there were some way to re-direct the goofy posts, but the only button I see says FLAG, and I'm not sure what that does. It would be nice if there were a DUMBASS button. Not so much to delete the posts, but just as a filter so I wouldn't have to wade through them looking for the sincere ones. I'll take any suggestions you have on this. Meanwhile, back to you ... (Wizard, please feel free to jump in if you see a weak argument!)
(1) 100% Correct. I couldn't have said it better.
(2) Traffic jam! LOL. OK, here's the deal. Most of us, when confronted with a "symmetric" problem, tend to expect a "symmetric" solution. In fact, this problem qualifies *except* that the problem (a square) is 4-way symmetric (under rotation) and each solution is only two-way symmetric. I believe that's key to making this problem so difficult, and why, for example, people gravitate toward the "X" instead of an "H" or even "U" pattern.
(3) I think you've got the basic idea for "why no curved segments"? I think you were looking at particular ones and realizing you could do better. Let me just generalize that thought a bit and consider *any* portion of *any* curved segment you may be considering. Cannot you always do better by replacing an arbitrary segment with a chord which connects the endpoints? If you believe that, the conclusion is that no curves will ever help you in this domain.
(4) Yes, yes and yes! Like you said, "<the x pattern> nearing the center becomes wasteful". I'm certain you're making a "local density" argument based on "too much pavement used over too little area in the center.
Well played, my friend! Thank you for your astute observations and insights. I'm glad you enjoyed it.
Quote: TranscendYou may want to click on quote rather than reply so people know who you are talking to
Yes, I screwed up. I'll try to fix that now. Thank you!
Is there a way I can "un-post" one of my own earlier posts (e.g. the ones where I failed to Quote my sources)? I hit EDIT but I don't think either SAVE or CANCEL will do it--unless I manually clear the content and hit SAVE, but would that actually delete the original post or just show it with zero content?
Quote: dblanch256Dear Wizard (may I call you Wizard?),
I prefer to think of it as [1 + sqrt(3)] but I assume you chose the expanded form because it's easier to see it's components.
You were to modest to point out that your solution is actually optimal, but one of the readers did. I should thank him for that.
Secretly I meant "You were TOO modest ..."
Quote: dblanch256Yes, I screwed up. I'll try to fix that now. Thank you!
Is there a way I can "un-post" one of my own earlier posts (e.g. the ones where I failed to Quote my sources)? I hit EDIT but I don't think either SAVE or CANCEL will do it--unless I manually clear the content and hit SAVE, but would that actually delete the original post or just show it with zero content?
You cannot delete a post it is not allowed to be blank as far as I know but simply typing deleted into it should suffice....but then again maybe you can, I am still fairly new to these forums.
Quote: dblanch256Quote: dblanch256Dear Wizard (may I call you Wizard?),
I prefer to think of it as [1 + sqrt(3)] but I assume you chose the expanded form because it's easier to see it's components.
You were to modest to point out that your solution is actually optimal, but one of the readers did. I should thank him for that.
Secretly I meant "You were TOO modest ..."
Seriously, to all reading this, is it customary to start a new thread for a new challenge, or does netiquette require continuing to add
related topics (e.g. new problems) to this same thread. If so, how? All I see is the option is to REPLY to existing posts here, and
it wouldn't really be a REPLY (to me or anyone else) to introduce a new challenge. "Anyone? Anyone? Anyone? ... "
Quote: dblanch256Seriously, to all reading this, is it customary to start a new thread for a new challenge, or does netiquette require continuing to add
related topics (e.g. new problems) to this same thread. If so, how? All I see is the option is to REPLY to existing posts here, and
it wouldn't really be a REPLY (to me or anyone else) to introduce a new challenge. "Anyone? Anyone? Anyone? ... "
Reply would be just a fresh post in the thread, I don't see why you couldn't post a new problem in this thread... Considering it would be on topic
My Master's dissertation had some work on Steiner trees.
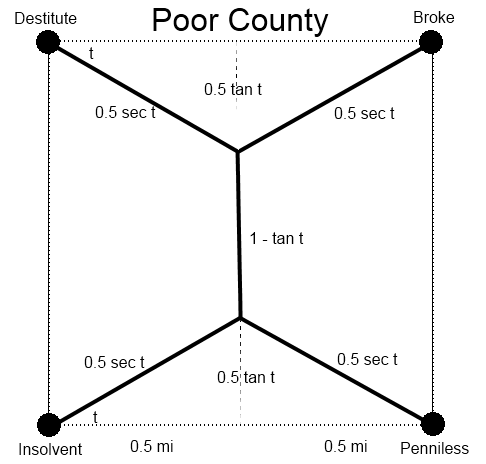
Total Distance = 1 + 2 sec t - tan t
Take Derivative set equal to 0:
2 sec t tan t - (sec t)^2 = 0
sec t (2 tan t - sec t) = 0
sec t = 0 or (2 tan t - sec t) = 0
sec t = 0 impossible
(2 tan t - sec t) = 0
2 (sin t/cos t) = 1/cos t
sin t = 1/2
t = 30 degrees
Total distance = 1 + 2 sec 30 - tan 30 = 1 + 4/sqrt (3) - 1/sqrt(3) = 1 + 3/Sqrt(3) = 1 + sqrt(3) = 2.732051 miles
Cost: $2,732,051 Budget: $2.75M Bonus for me to blow in Vegas: $17,949!!!
Quote: tringlomaneLate to the game, but doing it anyway. Slightly humorous diagram inside:
Total Distance = 1 + 2 sec t - tan t
Take Derivative set equal to 0:
2 sec t tan t - (sec t)^2 = 0
sec t (2 tan t - sec t) = 0
sec t = 0 or (2 tan t - sec t) = 0
sec t = 0 impossible
(2 tan t - sec t) = 0
2 (sin t/cos t) = 1/cos t
sin t = 1/2
t = 30 degrees
Total distance = 1 + 2 sec 30 - tan 30 = 1 + 4/sqrt (3) - 1/sqrt(3) = 1 + 3/Sqrt(3) = 1 + sqrt(3) = 2.732051 miles
Cost: $2,732,051 Budget: $2.75M Bonus for me to blow in Vegas: $17,949!!!
Very impressive. Just one question--the hardest part of this problem for most people is to envision the essential geometry of the solution in the first place.
Most people try a variety of configurations (the most popular being "X", "H" and "U") before they try hybrids (in this case, X "morphed" with "H").
So what got you past that first critical step and onto what I'd characterize as an elegantly optimal (and correct) solution?
Also, if you'll permit me, how would you answer the following related questions I posed to an earlier reader:
(1) What is "the other" solution? [I'm choosing my words very carefully here]
(2) In what way is the solution (either one) "counter-intuitive" with respect to the original problem?
(3) Why (in simple English) must the optimal solution contain (or not contain) any curved segments?
(4) Why (in simple English) does the optimal solution beat the more obvious "X" pattern? Putting it another way,
what is it about the "X" pattern that is "wasteful" relative to the optimal pattern?
Again, congrats on a job well done!
Quote:(4) Why (in simple English) does the optimal solution beat the more obvious "X" pattern? Putting it another way,
what is it about the "X" pattern that is "wasteful" relative to the optimal pattern?
The reason why X cannot be optimal is related to the fact that such problems must exhibit angles of 120° in order to be optimal. In three dimensions, it is still harder. I don't remember the values of angles (there are two) but you find it in the works of (Belgian) Joseph Plateau who analyzed soap bubbles.
Quote: dblanch256...
(1) What is "the other" solution? [I'm choosing my words very carefully here]
(2) In what way is the solution (either one) "counter-intuitive" with respect to the original problem?
...
The other solution is the first solution rotated 90 degrees. Either solution is counter-intuitive because the original problem has 4-fold symmetry but each solution has only mirror symmetry and 2-fold symmetry.
Quote: ChesterDogQuote: dblanch256...
(1) What is "the other" solution? [I'm choosing my words very carefully here]
(2) In what way is the solution (either one) "counter-intuitive" with respect to the original problem?
...
The other solution is the first solution rotated 90 degrees. Either solution is counter-intuitive because the original problem has 4-fold symmetry but each solution has only mirror symmetry and 2-fold symmetry.
Elegantly stated, and correct.
Explain why, for every similar problem of N points in 2D-space to be linked by a minimal length of 'road', the solution always implies straight segments (easy) and three-way 120° crossroads* (hard).
*Except at the original points, of course.
Quote: kubikulannLook, boy. You want a tough problem, here is one.
Explain why, for every similar problem of N points in 2D-space to be linked by a minimal length of 'road', the solution always implies straight segments (easy) and three-way 120° crossroads* (hard).
*Except at the original points, of course.
Part I: Because if any portion with curvature can always be shortened by replacing it with a "chord" connecting its endpoints.
Part II:
This results from an examination of the Euclidean Steiner Problem (ESP). The ESP has its roots in the so-called Fermat Problem (FP). However, the Initial FP (IFP) dealt only with three points, of necessity, on a two dimensional plane. The General Fermat Problem (GFP) was the logical extension to n points. The goal, in both cases, was to find a single (connected) network (N) of line segments (edges) which (a) connect all of the initial (terminal) points using a single network and (b) achieve a minimal total network length.
Note: It is required, for all but trivial cases, to add additional "intermediary points" as line segment (edge) vertices. Also, the treatment below is tailored for a two-dimensional plane, although I'm led to believe that extensions of the concept to higher dimensions are possible.
Consider a two dimensional Network (N) which connects a set of n terminal points in the 2-D Euclidean plane. We'll denote any additional point (vertex) we add to N as a Steiner Point (SP). The "degree" of any SP is defined as the number of edges (line segments) it has.
First, we need show why our augmented "optimal" network" N need only be a tree, as opposed to a graph. Whereas a graph may contain circularities. trees are a subset of graphs which, by definition do not contain them. We know that the shortest network for this problem must be a tree because if a "cycle" exists, deleting any points whose corresponding edges form any part of that cycle can only decrease the length of the network.
The general class of our solution is called Stiener Tree (due to addition of Steiner Points (SPs)). However, not all Steiner Trees are optimal. We seek not merely a Steiner Tree (ST), but a Steiner Minimal Tree (SMT) which we'll define to be a Steiner Tree whose length cannot be shortened by any small perturbation of its SPs (including splitting SPs to add additional segments).
We can now begin to narrow the field of SPs which will result in the SMT we seek. We start by consider the various possible order (defined above) of SPs we might use.
A SP of degree one satisfies nothing since, in railroad terms, it is essentially a "spur line" to nowhere, and thereby adds no connectivity value with respect to connecting the terminal points. It can therefore be eliminated to achieve a reduction in network size corresponding to the length of its single edge.
A SP of degree two can also be deleted, by replacing the two edges with a single edge connecting the two adjacent vertices, without increasing the length of the network. In railroad terms, removing a rail station (and, if necessary, re-routing the track to connect its two adjacent stations) can only decrease the track length, or in the trivial case of co-linear stations, offer no improvement.
The observations above indicate that all "potentially useful" SPs must therefore have a degree of at least three. We will now show why they must be exactly order three and and also why the angle of their edges must always be 120 degrees.
Suppose two edges meet at a point (p) with an angle less than 120. In this case, we can shorten the network by selecting points a and b on the two edges such that |a-p| = |b-p| respectively and construct a replacement Steiner Point (p') within the triangle "abp" (at the so-called Torricelli point). I'm not going to explain the Torricelli point here, unless requested, other than to say it is the point within any triangle which both minimizes the distances to the vertices and has the invariant feature that all angles formed by its adjacent edges are exactly 120 degrees.
Given the above, we can now safely rule out any SPs of order four or higher since they will always contain some angle between their edges of 90 degrees or less, which contradicts the construction technique described in the previous paragraph. Therefore all of our SPs will be of order three (have exactly three three edges each of which will form a 120 angle with its neighbors.
Example of a Steiner Minimal Tree (MST) joining six terminal points (shown as black shaded circles) using three optimal Steiner Points (shown as white shaded circles):

Quote: kubikulannKudos!
Well, nobody ever said you didn't know your stuff! And, I confess, I learned something useful and satisfying in the process.
Before you had mentioned the "120 degree feature" of all optimal SP trees, I had resorted to calculus to calculate the length of the "extra segment" which minimize the square network. Now, I'm thinking that trig would have been a much quicker route to the solution!
Thanks for that.
Another elegant solution is consider strings from A B and C connected to a ring. The string goes through holes at each town whereby hangs a weight (of 1Kg say). When the system comes to equilibrium the weights, in total, are the lowest (otherwise there would be a net force where one weight would be lower more than another weight(s) higher) and this is similar to the length of roads. At this time the net force, each being 1Kg, on the ring must be zero; so the angles must be 120 deg.
Back to the square, means the roads must meet at 120 deg (otherwise there's a better solution), and this leads to the answer.
(i) AE (i.e. distance from A to first junction) is .5 (distance on half the square) * 2/SQRT(3) (using 1,2,SQRT(3) triangle) = 1/SQRT(3).
(ii) AE+BF+other two = 4/SQRT(3).
(iii) EF = size of square - (AE/2) - (BF/2) = 1 - 1/SQRT(3).
Total = 4/SQRT(3) + 1 - 1/SQRT(3) = 3/SQRT(3)+1 = SQRT(3)+1.
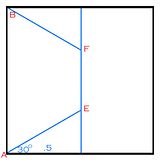
Quote: charliepatrickMany years ago someone set a puzzle in the works Christmas magazine to ask for a proof that the shortest distance between any three points was either two straight lines or had an angle of 120 deg. Ignoring the silly solutions, the easiest way to think about it was using symmetry at the junction.
Another elegant solution is consider strings from A B and C connected to a ring. The string goes through holes at each town whereby hangs a weight (of 1Kg say). When the system comes to equilibrium the weights, in total, are the lowest (otherwise there would be a net force where one weight would be lower more than another weight(s) higher) and this is similar to the length of roads. At this time the net force, each being 1Kg, on the ring must be zero; so the angles must be 120 deg.
Back to the square, means the roads must meet at 120 deg (otherwise there's a better solution), and this leads to the answer.
(i) AE (i.e. distance from A to first junction) is .5 (distance on half the square) * 2/SQRT(3) (using 1,2,SQRT(3) triangle) = 1/SQRT(3).
(ii) AE+BF+other two = 4/SQRT(3).
(iii) EF = size of square - (AE/2) - (BF/2) = 1 - 1/SQRT(3).
Total = 4/SQRT(3) + 1 - 1/SQRT(3) = 3/SQRT(3)+1 = SQRT(3)+1.
So we might call this the "minimum energy" approach? Well played!


