February 27th, 2013 at 6:09:26 AM
permalink
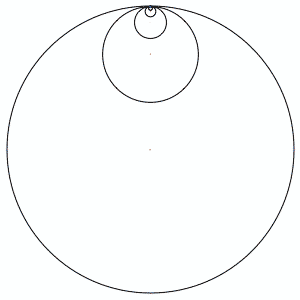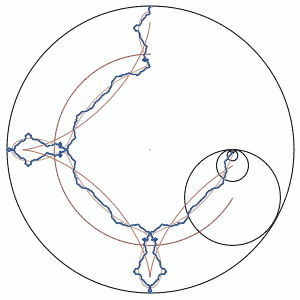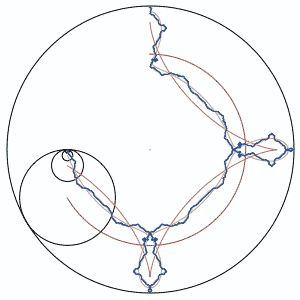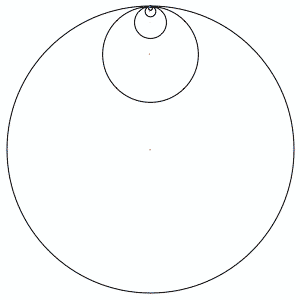
In the above animation, each circle's radius is 1/3 the size of the next larger circle. Relatively, they rotate at -3 times the speed of the next largest circle. There is a "pen" in the center of each circle, which draws as it moves.
The pink lines show the first few circles' paths, and the blue path is drawn by the (theoretically) smallest circle. It seems to behaves in a fractal-like manner.
Is there a name for this curve?
-Dween!
February 27th, 2013 at 6:11:02 AM
permalink
February 27th, 2013 at 6:22:43 AM
permalink
I am aware of the Spirograph toy, and understand that there is a correlation. However, I am interested in the blue curve, which is created with an infinite number of circles embedded within one another, rotating in complex ways, unable to be replicated with a Spirograph.
-Dween!
February 27th, 2013 at 6:35:16 AM
permalink
I apologize. It was a quip/joke. I'm just trying to be like Buzzard. LOL. Sorry for the distraction and good luck finding your answer. I would be surprised if there is already a name for it though. Interesting stuff nevertheless.
aahigh.com
February 27th, 2013 at 10:06:55 AM
permalink
Quote: DweenI am interested in the blue curve, which is created with an infinite number of circles embedded within one another. . .
Firstly, it's not an infinate number of circles. I expect that if you add another circle, it's path will mimic the blue path unless you magnify the image.
I don't know what to call it but I do not think "fractals" is right. I'm leaning more towards "chaos" but don't think that's right either.
On a side note, count the circles. It took me several attempts to count them all, ans to match all of them to their paths.
I invented a few casino games. Info:
http://www.DaveMillerGaming.com/ �������������������������������������
Superstitions are silly, irrational, childish rituals, born out of fear of the unknown. But how much does it cost to knock on wood? 😁
February 27th, 2013 at 2:56:20 PM
permalink
Quote: AhighI apologize. It was a quip/joke.
The original post is a joke? Why ask such a question here?
I think that this is a fractal with inbuilt feedback, as a theoretical reverse means to generate basic nuclear processes. Were foamy space-time to give rise to particles.
Those who can, do; those who can't, teach. But those who confuse the two... they wind up on the internet.
February 27th, 2013 at 3:11:58 PM
permalink
Ahigh: I thought you were perhaps joking, but at the same time you weren't far off. No harm, no foul! :)
DJ: In the picture, there are only 4 or 5 circles, but I discovered that it is an infinite summation that produces the curve, sort of like a Koch's snowflake. You only need about 7 iterations to get a decent looking curve, though.
I have recreated it using Flash, without the circles.

The blue circle is iteration 1.
The magenta diamond shape is iteration 2.
The red shape with the "bowling pins" near the compass points is iteration 3.
The black curve is iteration 7.
I have determined a Cartesian summation based on the polar coordinates. It is easier to express it in Cartesian calculations than in polar:
Not the most elegant pseudo-code, but I hope it gets the point across.
DJ: In the picture, there are only 4 or 5 circles, but I discovered that it is an infinite summation that produces the curve, sort of like a Koch's snowflake. You only need about 7 iterations to get a decent looking curve, though.
I have recreated it using Flash, without the circles.

The blue circle is iteration 1.
The magenta diamond shape is iteration 2.
The red shape with the "bowling pins" near the compass points is iteration 3.
The black curve is iteration 7.
I have determined a Cartesian summation based on the polar coordinates. It is easier to express it in Cartesian calculations than in polar:
Define r0 := 2/3 the size of the radius of the large circle
Define r1 := 1/3 r0
Define r2 := 1/3 r1
Generalize: Define rn := 1/3 rn-1
iteration 1:
for all Θ = 0 to 2π,
x = cos(Θ)*r0
y = sin(Θ)*r0
iteration 2:
for all Θ = 0 to 2π,
x = cos(Θ)*r0 + cos(-3Θ)*r1
y = sin(Θ)*r0 + sin(-3Θ)*r1
iteration 3:
for all Θ = 0 to 2π,
x = cos(Θ)*r0 + cos(-3Θ)*r1 + cos(9Θ)*r2
y = sin(Θ)*r0 + sin(-3Θ)*r1 + sin(9Θ)*r2
Generalize: iteration n:
for all Θ = 0 to 2π, and for all m = 0 to n
x = Σ cos((-3)mΘ)*rm
y = Σ sin((-3)mΘ)*rm
-Dween!
February 27th, 2013 at 3:20:17 PM
permalink
SQUIGGLY ?
Shed not for her
the bitter tear
Nor give the heart
to vain regret
Tis but the casket
that lies here,
The gem that filled it
Sparkles yet
February 27th, 2013 at 3:43:27 PM
permalink
Wikipedia suggests it is a form of Roulette (more specifically a sort of Centred Trochoid
Maybe?
Kind of neat.
Maybe?
Kind of neat.
"Then you can admire the real gambler, who has neither eaten, slept, thought nor lived, he has so smarted under the scourge of his martingale, so suffered on the rack of his desire for a coup at trente-et-quarante" - Honore de Balzac, 1829
February 28th, 2013 at 5:40:40 AM
permalink
Roulettes or trochoids are usually meant to account for only ONE circle (maybe two) attached to the master circle.
Here the idea is indeed that you go to infinity.
I don't know whether this can be technically considered a fractal, in the sense that fractal is supposed to include the notion of pattern reproduction at lower levels. But on the other hand it is certainly in the same family as the Koch flake, which is a fractal.
More semantic than useful, though. Did you investigate the properties of your curve? That's what is interesting!
Here the idea is indeed that you go to infinity.
I don't know whether this can be technically considered a fractal, in the sense that fractal is supposed to include the notion of pattern reproduction at lower levels. But on the other hand it is certainly in the same family as the Koch flake, which is a fractal.
More semantic than useful, though. Did you investigate the properties of your curve? That's what is interesting!
Reperiet qui quaesiverit
February 28th, 2013 at 12:06:09 PM
permalink
thecesspit:
It seems that "trochoid" and "roulette" indeed are the terms for this type of curve. Thank you for finding that out for me!
kubikulann:
Everything I have found has agreed with the notion that only one or two circles are involved in the creation of a trochoid. The original picture had no explanation to it; No formulas, no distances. I did some measuring, estimating, and guessing, and was able to figure out all of the associated radii and rotation speeds for each circle.
I haven't done any "zoomed in" versions of the curve, but want to look into it. I don't expect it to be a fractal per se (with repeating patterns), but I am interested in seeing what is happening near the compass points especially.
I am also working on a bit of a higher resolution, smoother animated gif of the curve, which might not come to fruition due to lack of tools in creating it.
It seems that "trochoid" and "roulette" indeed are the terms for this type of curve. Thank you for finding that out for me!
kubikulann:
Everything I have found has agreed with the notion that only one or two circles are involved in the creation of a trochoid. The original picture had no explanation to it; No formulas, no distances. I did some measuring, estimating, and guessing, and was able to figure out all of the associated radii and rotation speeds for each circle.
I haven't done any "zoomed in" versions of the curve, but want to look into it. I don't expect it to be a fractal per se (with repeating patterns), but I am interested in seeing what is happening near the compass points especially.
I am also working on a bit of a higher resolution, smoother animated gif of the curve, which might not come to fruition due to lack of tools in creating it.
-Dween!
February 28th, 2013 at 12:40:38 PM
permalink
I find it amusing that it is a type of (mathematical) roulette, based on the board you asked the question :)
"Then you can admire the real gambler, who has neither eaten, slept, thought nor lived, he has so smarted under the scourge of his martingale, so suffered on the rack of his desire for a coup at trente-et-quarante" - Honore de Balzac, 1829
March 1st, 2013 at 10:48:37 AM
permalink


