Quote: teliotAs for holes -- you've given only finitely many numbers on a continuous interval, and you ask if there are holes. Yikes!
Where did I ask if there were holes?
You are right, you didn't ask. You stated. Sorry for the misrepresentation.Quote: WizardWhere did I ask if there were holes?
Quote: March 29th, 2016 at 10:26:33 AMthose holes will be pretty tiny.
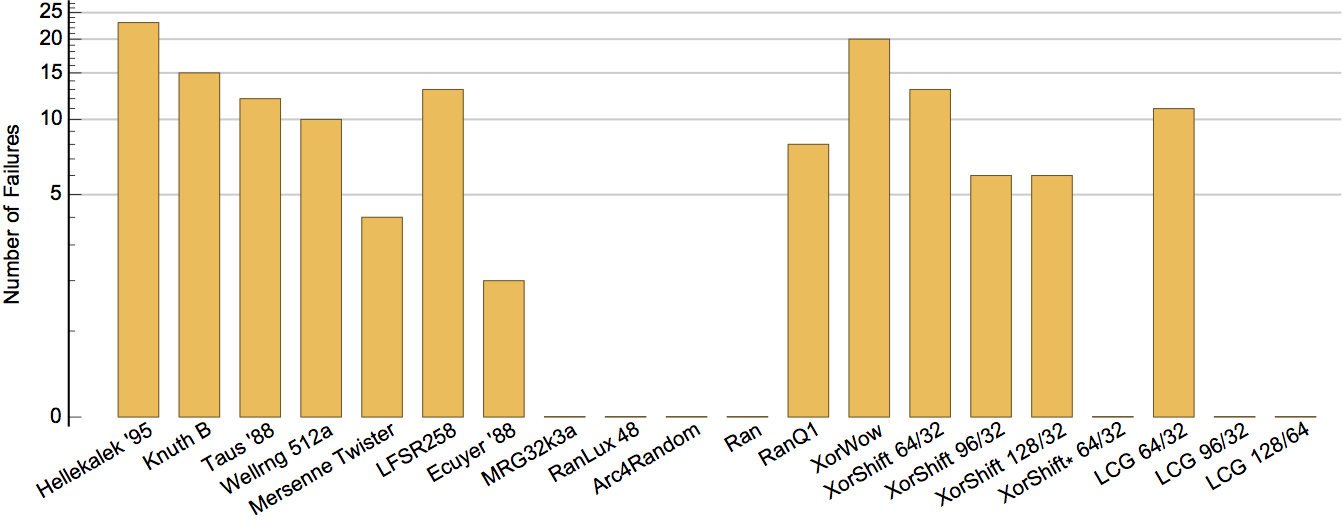
I don't know what the Big Crush test is but it is interesting as I use it for my simulations and use date/time to initialise it. I found this picture on http://www.pcg-random.org/statistical-tests.html but have never heard of the others ...Quote: teliot...the Big Crush tests...the Mersenne Twister doesn't pass...
btw when learning maths that was a concept ( https://en.wikipedia.org/wiki/%28%CE%B5,_%CE%B4%29-definition_of_limit ) for finding out whether a function F(x) had a limit (say 0) using the idea that given a small difference d from the limit one could find a value x such that F(x)<d. Similarly one could create a lots of random numbers and string them together to get extremely close.
Here's my hypothesis:Quote: teliotI would hardly know where to begin to compute the EV of the game using the Mersenne Twister as the RNG and 64 bit representations for the doubles in the range [0,1].
Let EV1 be the EV of the game derived by using mt19937 and IEEE 754 64-bit doubles.
We know that the true EV of the game is e
Let d = |e - EV1|
I submit that 1/d >> M2, where M2 is the global money supply (and ">>" means "much greater than" rather than "right shift")
In other words, the quantization of money is far larger than the quantization of the underlying approximation of the random process. That implies that, for amounts wagerable with actual money, the expected results would be indistinguishable regardless of whether you're playing with a perfect [0,1] generator or the MT-based approximation. In short, you'll never be able to tell the difference.
Agree.Quote: MathExtremistHere's my hypothesis:
Let EV1 be the EV of the game derived by using mt19937 and IEEE 754 64-bit doubles.
We know that the true EV of the game is e
Let d = |e - EV1|
I submit that 1/d >> M2, where M2 is the global money supply (and ">>" means "much greater than" rather than "right shift")
.
Very nice, I have not seen that before.Quote: charliepatrick
Quote: teliotYou are right, you didn't ask. You stated. Sorry for the misrepresentation.
Between that and telling me that 1+1!=5 in the last math thread, I think you should sometimes pause and reflect how your words can hurt people before clicking the "enter" button.
you are no doubt right about pausing, but I don't recall the equation you are referring to. Would you help me out by telling me when I said that?Quote: WizardBetween that and telling me that 1+1!=5 in the last math thread, I think you should sometimes pause and reflect how your words can hurt people before clicking the "enter" button.
Quote: teliotWould you help me out by telling me when I said that?
First, let me correct myself. What I allege is that you had to tell me that 5 <> 0.
It was this post, in particular the statement, "Hence you conclude that x = 1 must be a solution to the original polynomial f(x)."
As a reminder, the original equation was 1+x+x^2+x^3+x^4 = 0.
If I claimed that x=1, then I would also obviously be claiming that 5=0, which is what I felt was very insulting.
Here's the pre-publication paper that's taken from:Quote: teliotVery nice, I have not seen that before.Quote: charliepatrick
http://www.pcg-random.org/pdf/toms-oneill-pcg-family-v1.02.pdf
I don't know why it bothers me that others want to argue trivialities, like 0^0, or 0! or 0.9999... = 1, or the thread above. I sometimes make the mistake of chiming in (I believe you invited me to the thread above). I mean no harm and apologize for any disrespect I showed to you in my response. It's best for me to just avoid such threads. They aggravate me beyond reason.Quote: WizardFirst, let me correct myself. What I allege is that you had to tell me that 5 <> 0.
It was this post, in particular the statement, "Hence you conclude that x = 1 must be a solution to the original polynomial f(x)."
As a reminder, the original equation was 1+x+x^2+x^3+x^4 = 0.
If I claimed that x=1, then I would also obviously be claiming that 5=0, which is what I felt was very insulting.
Mike, you might really enjoy the NumberPhile youtube posts. They get to the heart of a lot of very interesting mathematics in a way that the educated non-theorist can easily understand. For example, the opposite of infinity:
https://www.youtube.com/watch?v=WYijIV5JrKg
Or my personal favorite:
https://www.youtube.com/watch?v=_s5RFgd59ao
Quote: MathExtremistHere's my hypothesis:Quote: teliotI would hardly know where to begin to compute the EV of the game using the Mersenne Twister as the RNG and 64 bit representations for the doubles in the range [0,1].
Let EV1 be the EV of the game derived by using mt19937 and IEEE 754 64-bit doubles.
We know that the true EV of the game is e
Let d = |e - EV1|
I submit that 1/d >> M2, where M2 is the global money supply (and ">>" means "much greater than" rather than "right shift")
In other words, the quantization of money is far larger than the quantization of the underlying approximation of the random process. That implies that, for amounts wagerable with actual money, the expected results would be indistinguishable regardless of whether you're playing with a perfect [0,1] generator or the MT-based approximation. In short, you'll never be able to tell the difference.
Nice summary of theoretical RNG considerations vs the real world.
Eliot, have you used or researched random.org for "true" random numbers?
I haven't visited the site in years. My father invented a true RNG when he worked for the army in WW-II. He had a degree as an electrical engineer and he had the idea of filtering white noise to generate random 0's and 1's. Now this "true" RNG seems rather well-known (Google search).Quote: AcesAndEights[Eliot, have you used or researched random.org for "true" random numbers?


