Quick Quads Oddity
Thread Rating:
April 8th, 2021 at 6:26:14 AM
permalink
So, I'm basically posting to try out the new picture post feature, but I thought I'd share a shot I took at Harrah's New Orleans back in July 2019, which, because of Covid, was my last casino trip to date.
So, Mrs. Joeman is not a big gambler, but she has taken a liking to Quick Quads VP. We typically play DDB, and one of the things we do when we play together is that if either is dealt trips, we will stop and get the other's attention before the draw so that we can both root for quads to show up.
Well, on this occasion, I, playing on the right hand machine, was dealt a pair of 9's plus two cards that added up to 9 -- essentially dealt trips in Quick Quads. As I look up to get Mrs. Joeman's attention, I see that she has been dealt essentially the same hand!
After a second or two to realize that we have been dealt the same hand, we decide to push the draw button at the same time, and... Boom! We both hit Quick Quads on the same line! What are the odds?
So, Mrs. Joeman is not a big gambler, but she has taken a liking to Quick Quads VP. We typically play DDB, and one of the things we do when we play together is that if either is dealt trips, we will stop and get the other's attention before the draw so that we can both root for quads to show up.
Well, on this occasion, I, playing on the right hand machine, was dealt a pair of 9's plus two cards that added up to 9 -- essentially dealt trips in Quick Quads. As I look up to get Mrs. Joeman's attention, I see that she has been dealt essentially the same hand!
After a second or two to realize that we have been dealt the same hand, we decide to push the draw button at the same time, and... Boom! We both hit Quick Quads on the same line! What are the odds?
"Dealer has 'rock'... Pay 'paper!'"
April 8th, 2021 at 7:37:33 AM
permalink
I get a 1 in 25.6 million chance for those specific conditions (exactly three 9s and no full house on the same hand on both machines, and both make quick quads)
Prob(three 9s on a specific hand, and not a full house) = 4 x (C(48,2) - 12 x 6) / 2,598,960 = 88 / 54,145
Prob(making a quick quad) depends on the cards dealt (there are 1056 pairs):
If both of the cards were 10-K and not a pair: (96)
8A, 72, 63, 54 = 64 / 1081
If one card is an Ace, and the other is a 10: (512)
8A (12), 72 (16), 63 (16), 54 (16) = 60
If one is an Ace and the other is a 7: (384)
8A (12), 72 (12), 63 (16), 54 (16) = 56
If one is an Ace and the other is an 8: (64)
8A (9), 72 (16), 63 (16), 54 (16) = 57
Prob(making a quick quad from three 9s) = (96 x 64 + 512 x 60 + 384 x 56 + 64 x 57) / (1056 x 1081) = 646 / 11,891
Prob(being dealt 3 9s and not a full house on one machine) = 5 x 88 / 54,145 = 88 / 10,829
Prob(being dealt the same thing on the same hand on the other machine) = 88 / 54,145
Prob(making a quick quad on both) = (646 / 11,891)^2
Total = about 1 / 25,653,882
Prob(three 9s on a specific hand, and not a full house) = 4 x (C(48,2) - 12 x 6) / 2,598,960 = 88 / 54,145
Prob(making a quick quad) depends on the cards dealt (there are 1056 pairs):
If both of the cards were 10-K and not a pair: (96)
8A, 72, 63, 54 = 64 / 1081
If one card is an Ace, and the other is a 10: (512)
8A (12), 72 (16), 63 (16), 54 (16) = 60
If one is an Ace and the other is a 7: (384)
8A (12), 72 (12), 63 (16), 54 (16) = 56
If one is an Ace and the other is an 8: (64)
8A (9), 72 (16), 63 (16), 54 (16) = 57
Prob(making a quick quad from three 9s) = (96 x 64 + 512 x 60 + 384 x 56 + 64 x 57) / (1056 x 1081) = 646 / 11,891
Prob(being dealt 3 9s and not a full house on one machine) = 5 x 88 / 54,145 = 88 / 10,829
Prob(being dealt the same thing on the same hand on the other machine) = 88 / 54,145
Prob(making a quick quad on both) = (646 / 11,891)^2
Total = about 1 / 25,653,882
April 8th, 2021 at 9:17:51 AM
permalink
Wow! Thanks for the analysis, TDG. I should have known that when I say, "What are the odds?" around here, it is not taken rhetorically!
"Dealer has 'rock'... Pay 'paper!'"
April 8th, 2021 at 2:09:09 PM
permalink
Quote: ThatDonGuyI get a 1 in 25.6 million chance for those specific conditions (exactly three 9s and no full house on the same hand on both machines, and both make quick quads)
Prob(three 9s on a specific hand, and not a full house) = 4 x (C(48,2) - 12 x 6) / 2,598,960 = 88 / 54,145
Prob(making a quick quad) depends on the cards dealt (there are 1056 pairs):
If both of the cards were 10-K and not a pair: (96)
8A, 72, 63, 54 = 64 / 1081
If one card is an Ace, and the other is a 10: (512)
8A (12), 72 (16), 63 (16), 54 (16) = 60
If one is an Ace and the other is a 7: (384)
8A (12), 72 (12), 63 (16), 54 (16) = 56
If one is an Ace and the other is an 8: (64)
8A (9), 72 (16), 63 (16), 54 (16) = 57
Prob(making a quick quad from three 9s) = (96 x 64 + 512 x 60 + 384 x 56 + 64 x 57) / (1056 x 1081) = 646 / 11,891
Prob(being dealt 3 9s and not a full house on one machine) = 5 x 88 / 54,145 = 88 / 10,829
Prob(being dealt the same thing on the same hand on the other machine) = 88 / 54,145
Prob(making a quick quad on both) = (646 / 11,891)^2
Total = about 1 / 25,653,882
EDIT; I am not familiar with Quick Quads, Does the first deal occur on only one line, and then the draw occur on five lines? Or, on the initial deal, are there five different cards on each of the 5 lines?
So many better men, a few of them friends, are dead. And a thousand thousand slimy things live on, and so do I.
April 8th, 2021 at 2:38:04 PM
permalink
Quote: ThatDonGuyI get a 1 in 25.6 million chance for those specific conditions (exactly three 9s and no full house on the same hand on both machines, and both make quick quads)
Prob(three 9s on a specific hand, and not a full house) = 4 x (C(48,2) - 12 x 6) / 2,598,960 = 88 / 54,145
Prob(making a quick quad) depends on the cards dealt (there are 1056 pairs):
If both of the cards were 10-K and not a pair: (96)
8A, 72, 63, 54 = 64 / 1081
If one card is an Ace, and the other is a 10: (512)
8A (12), 72 (16), 63 (16), 54 (16) = 60
If one is an Ace and the other is a 7: (384)
8A (12), 72 (12), 63 (16), 54 (16) = 56
If one is an Ace and the other is an 8: (64)
8A (9), 72 (16), 63 (16), 54 (16) = 57
Prob(making a quick quad from three 9s) = (96 x 64 + 512 x 60 + 384 x 56 + 64 x 57) / (1056 x 1081) = 646 / 11,891
Prob(being dealt 3 9s and not a full house on one machine) = 5 x 88 / 54,145 = 88 / 10,829
Prob(being dealt the same thing on the same hand on the other machine) = 88 / 54,145
Prob(making a quick quad on both) = (646 / 11,891)^2
Total = about 1 / 25,653,882
OOPS - while the numbers are correct, they do not match the situation in two ways:
One, they are based on being dealt three 9s and drawing two cards, as opposed to dealt two 9s and two cards that add up to 9, and drawing for the third 9 to complete the quick quad.
Two, they are also based on each hand being dealt on its own, rather than all five hands on a machine being dealt the same hand.
This is a lot easier to figure out.
In the 2,598,960 possible deals, there are 6 ways to get a pair of 9s; for each one, there are 16 sets of A-8, 16 of 2-7, 16 of 3-6, and 16 of 4-5, for a total of 64; for each one of these, there are 40 cards (four each of the remaining 10 ranks) that can be the fifth card, for a total of 6 x 64 x 40 = 15,360 such deals.
The probability of drawing a 9 to complete the Quick Quad is 2/47.
The probability of being dealt such a hand is 15,360 / 2,598,960 = 64 / 10,829
The probability of it being dealt on side-by-side machines is (64 / 10,829)^2
For the first machine, the probability that a particular hand will draw a 9 is 2/47, and the probability that the same hand on the other machine will also draw a 9 is also 2/47, so the probability of having Quick Quads in a particular position on both machines is (2 / 47)^2.
The probability that at least one hand will have Quick Quads on both machines is about 5 times this, or 5 x (64 / 10,829)^2 x (2 / 47)^2 = 81,920 / 259,043,335,369, or about 1 / 3,162,150.
Last edited by: ThatDonGuy on Apr 8, 2021
April 8th, 2021 at 2:40:47 PM
permalink
It plays like any standard 5-line VP -- you only get dealt cards on the bottom line, then draw on 5 lines.Quote: gordonm888EDIT; I am not familiar with Quick Quads, Does the first deal occur on only one line, and then the draw occur on five lines? Or, on the initial deal, are there five different cards on each of the 5 lines?
The Quick Quads variant is that a hand consisting of a three-of-a-kind plus two cards whose values add up to the same rank as the trips qualifies as four-of-a-kind. E.g., 9-9-9-5-4 is paid as if it were quads. You pay an extra coin per hand for the feature. Actually, you could only play 5 coins per hand, and it is just regular 5-play VP.
"Dealer has 'rock'... Pay 'paper!'"
April 9th, 2021 at 4:46:57 AM
permalink
Quote: JoemanIt plays like any standard 5-line VP -- you only get dealt cards on the bottom line, then draw on 5 lines.
The Quick Quads variant is that a hand consisting of a three-of-a-kind plus two cards whose values add up to the same rank as the trips qualifies as four-of-a-kind. E.g., 9-9-9-5-4 is paid as if it were quads. You pay an extra coin per hand for the feature. Actually, you could only play 5 coins per hand, and it is just regular 5-play VP.
Thanks. I actually knew this. After looking at ThatDonGuy's math analysis, my question was intended as a tactful way of alerting him that he had erroneously analyzed the five lines as five separately dealt poker hands. He has subsequently corrected that analysis in his post above.
Here is a genuine question:
Assuming DDB, if you are dealt 4-4-3-3-A, do you discard the A and draw to two pair? Or discard one of the 3's and draw to 4-4-3-A?
So many better men, a few of them friends, are dead. And a thousand thousand slimy things live on, and so do I.
April 9th, 2021 at 5:48:10 AM
permalink
Whoa, that one went straight over my head! I'm glad TDG got it, though.Quote: gordonm888Thanks. I actually knew this. After looking at ThatDonGuy's math analysis, my question was intended as a tactful way of alerting him that he had erroneously analyzed the five lines as five separately dealt poker hands. He has subsequently corrected that analysis in his post above.
I showed this thread to Mrs. Joeman last night. She was amused that someone would actually run the numbers on this.
You'd drop one of the threes.Quote:Here is a genuine question:
Assuming DDB, if you are dealt 4-4-3-3-A, do you discard the A and draw to two pair? Or discard one of the 3's and draw to 4-4-3-A?
For DDB where (for 5-coin bet):
Quad 2's, 3's, 4's pays 400
Full House pays 45
Two Pair pays 5
Quad 2's, 3's, 4's pays 400
Full House pays 45
Two Pair pays 5
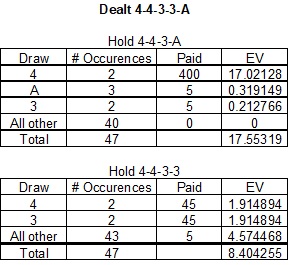
Now, a closer decision is a hand like 4-4-3-X-X. In DDB, you keep the 3 along with the pair of 4's. If it were 5-5-3-X-X, you only keep the pair of 5's.
I'll defer to Wiz for the math on this one.
"Dealer has 'rock'... Pay 'paper!'"
April 9th, 2021 at 6:45:46 AM
permalink
Quote: JoemanWhoa, that one went straight over my head! I'm glad TDG got it, though.
I showed this thread to Mrs. Joeman last night. She was amused that someone would actually run the numbers on this.
You'd drop one of the threes.For DDB where (for 5-coin bet):
Quad 2's, 3's, 4's pays 400
Full House pays 45
Two Pair pays 5
Now, a closer decision is a hand like 4-4-3-X-X. In DDB, you keep the 3 along with the pair of 4's. If it were 5-5-3-X-X, you only keep the pair of 5's.
I'll defer to Wiz for the math on this one.
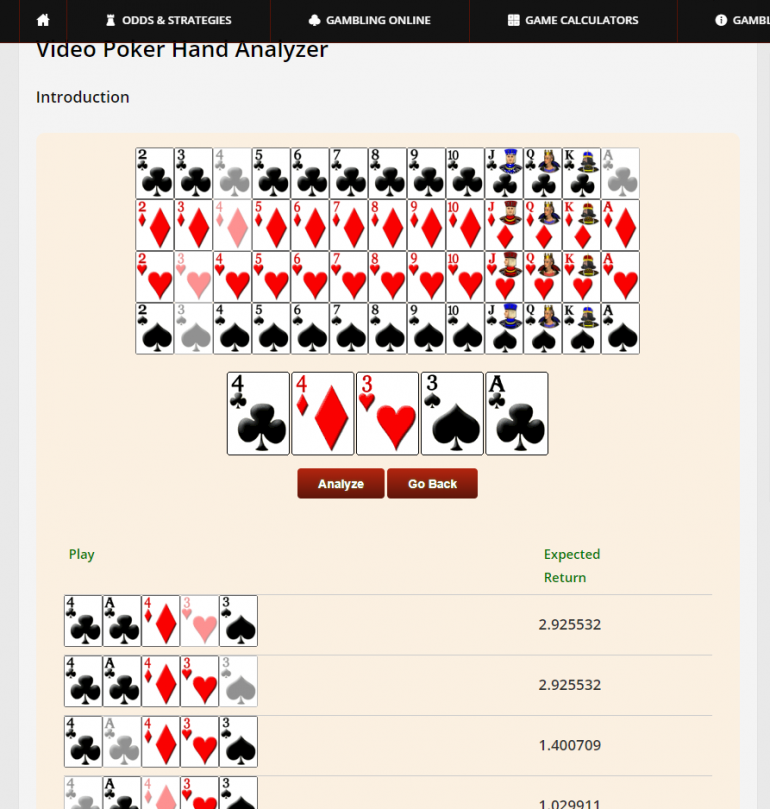
Here's a picture of the Wizard's video poker hand analyzer for double double bonus quick quads. Multiplying his numbers by 6 for the bet size verifies your answer.
https://wizardofodds.com/games/video-poker/hand-analyzer/
