Stack 'Em High Poker
Poll
 | 4 votes (44.44%) | ||
| | 3 votes (33.33%) | ||
| | 2 votes (22.22%) | ||
| | 2 votes (22.22%) | ||
| | 5 votes (55.55%) | ||
| | 4 votes (44.44%) | ||
| | 2 votes (22.22%) | ||
| | 2 votes (22.22%) | ||
| No votes (0%) | |||
| | 2 votes (22.22%) |
9 members have voted
January 6th, 2020 at 12:59:25 PM
permalink
One video poker variant I saw at G2E and now at VideoPoker.com is Stack 'em High Poker. Here are the rules:
Example
In this hand, I was dealt two aces, which I held. Note you must click on hold, it's not automatic.
In the five hands I paid for, none of them improved.
I was awarded 7 out of a maximum of 8 bonus hands. The second bonus hand improved to a three of a kind. Note how the aces of hearts was replicated to all hands above it. Had one of those improved to four aces, that fourth ace would have replicated too.
Without knowing the probability distribution of extra hands, it will be impossible to analyze. However, I am expecting the returns from Action Gaming.
The question for the poll is would you play Stack 'em Up Poker?
- Game is an optional feature on 3-play and 5-play video poker.
- The player must play 10 credits per line to invoke the feature. Wins will be based on 5 credits only.
- If the player is dealt 2 or 3 aces, then he will win additional hands above the 3 or 5 he paid for.
- The number of additional hands is not disclosed in the rules, except to state a maximum. For example, this maximum is 8 hands in 5-play Bonus Poker and 6 in Double Double Bonus.
- Regardless of how many hands the player has, they will be in the form of a vertical stack.
- Replacements cards are dealt to one hand at a time, starting at the bottom of the stack. If the player is dealt any additional aces on the draw, those aces will be sticky for all hands above.
- To invoke the feature, the player must hold the 2 or 3 dealt aces only. If the holds other cards, he won't get the bonus hands.
Example
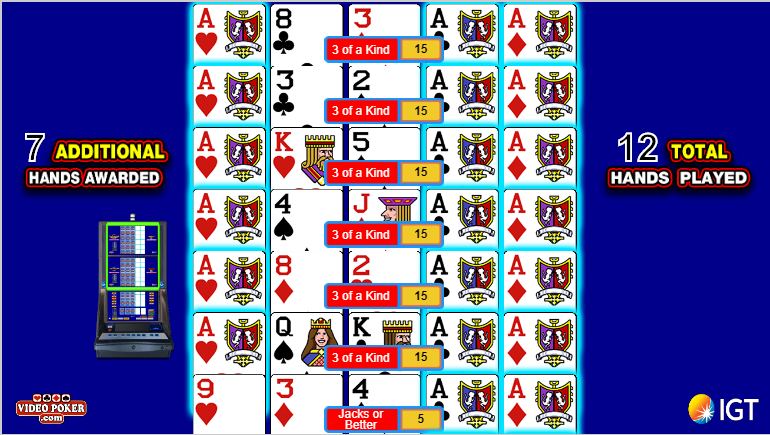
In this hand, I was dealt two aces, which I held. Note you must click on hold, it's not automatic.
In the five hands I paid for, none of them improved.
I was awarded 7 out of a maximum of 8 bonus hands. The second bonus hand improved to a three of a kind. Note how the aces of hearts was replicated to all hands above it. Had one of those improved to four aces, that fourth ace would have replicated too.
Without knowing the probability distribution of extra hands, it will be impossible to analyze. However, I am expecting the returns from Action Gaming.
The question for the poll is would you play Stack 'em Up Poker?
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
January 6th, 2020 at 3:58:30 PM
permalink
I'm very curious about this game. Would this game take advantage of a different cabinet? We see slot games taking advantage of this all the time on the casino floors now, but I'm still waiting for video poker to catch up to it.
January 6th, 2020 at 4:01:35 PM
permalink
You seem to have gotten about the same amount of interest in this that I got when I posted it a while back:
https://wizardofvegas.com/forum/gambling/video-poker/34065-new-game-at-videopoker-com-stack-em-high/#post750498
The rules are kind of ambiguous but when playing DW versions it's the "2" and not aces that get stacked, just in case anyone tries to play it.
https://wizardofvegas.com/forum/gambling/video-poker/34065-new-game-at-videopoker-com-stack-em-high/#post750498
The rules are kind of ambiguous but when playing DW versions it's the "2" and not aces that get stacked, just in case anyone tries to play it.
January 6th, 2020 at 4:43:00 PM
permalink
Quote: RealizeGamingI'm very curious about this game. Would this game take advantage of a different cabinet? We see slot games taking advantage of this all the time on the casino floors now, but I'm still waiting for video poker to catch up to it.
As I recall from G2E, it uses a second screen above the main one for the bonus hands. In other words, it would need a special cabinet. However, I may be wrong.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
January 6th, 2020 at 5:36:31 PM
permalink
Correction
Contrary to what I wrote before, the number of extra plays is always the same for any given game, pay table, and number of original plays. This is good news is it makes the math quantifiable. I'm on it!
Please see my work in progress page on Stack 'em High poker for the number of extra plays.
Contrary to what I wrote before, the number of extra plays is always the same for any given game, pay table, and number of original plays. This is good news is it makes the math quantifiable. I'm on it!
Please see my work in progress page on Stack 'em High poker for the number of extra plays.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
January 7th, 2020 at 6:35:40 AM
permalink
I think I have a small math error somewhere, as I'm showing this feature slightly lowers EV. As an example of my math, the following table shows the probability of having a 2, 3, or 4 aces at the end of each hand in a 12-hand feature, starting with a pair of aces and discarding three singletons.
Can anyone confirm or deny?
I know there are 3 classes of two aces and 2 glasses of 3 aces on the deal, so this is just an example.
| Hand | 2 aces | 3 aces | 4 aces |
|---|---|---|---|
| 1 | 0.875116 | 0.122109 | 0.002775 |
| 2 | 0.765827 | 0.223660 | 0.010513 |
| 3 | 0.670188 | 0.307450 | 0.022363 |
| 4 | 0.586492 | 0.375919 | 0.037590 |
| 5 | 0.513248 | 0.431190 | 0.055562 |
| 6 | 0.449151 | 0.475115 | 0.075734 |
| 7 | 0.393059 | 0.509303 | 0.097637 |
| 8 | 0.343972 | 0.535156 | 0.120872 |
| 9 | 0.301016 | 0.553890 | 0.145094 |
| 10 | 0.263423 | 0.566565 | 0.170012 |
| 11 | 0.230526 | 0.574098 | 0.195376 |
| 12 | 0.201737 | 0.577287 | 0.220976 |
| Total | 5.593755 | 5.251742 | 1.154503 |
Can anyone confirm or deny?
I know there are 3 classes of two aces and 2 glasses of 3 aces on the deal, so this is just an example.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
January 7th, 2020 at 1:09:26 PM
permalink
Quote: WizardCan anyone confirm or deny?
I get the same values. But just so we are all on the same page, here are where my numbers come from in case someone can spot a flaw in my logic.
First line:
The probability of no new aces is (45*44*43)/(47*46*45) = 0.8751156
The probability of getting an ace in position 1 is 2 * 45 * 44/(47*46*45). Multiply by 3 (the 3 possible ending positions) to get the overall probability of 1 ace = 0.12210916.
The probability of getting 2 aces is 1 minus the sum of the no and one ace = 1 - 0.8751156 - 0.12210916 = 0.00277524
Second line:
If we have just 2 aces, the three probabilities are the same as above. Call these A.
If we have 3 aces, the probability of ending with 2 aces is zero. The probability of ending with 3 is 45*44/(46*45) = 0.956521739. The probability of ending with 4 is just the remainder = 0.04347826. Call these B.
If we have 4 aces, the probability of ending with 2 or 3 is zero and the probability of 4 is 1. Call these C.
Now we have to take into account the likelihood of A, B and C. That is, we apply the starting probabilities. Thus we get 0.8751156A + 0.12210916B + 0.00277524C which gives
0.765827 0.22366 0.010513
Row 3 would be similar but starting with these values for the likelihood of the current number of aces. And so on.
January 7th, 2020 at 6:28:43 PM
permalink
Quote: GaryJKoehlerI get the same values.
I didn't see any flaws and think we did it the same way. The fact that we agree says a lot. I have a feeling any error I made is probably in setting up the various situations the player can get two aces. What the player throws away affects the subsequent hands.
Let me go a bit further.
If the player gets AAxyz (two aces and three singletons), here is the value of the subsequent 12-hand bonus.
| Hand | Pays | Expected | Win |
|---|---|---|---|
| High pair | 1 | 4.556604125 | 4.556604125 |
| Two pair | 2 | 1.021776788 | 2.043553576 |
| Three of a kind | 3 | 4.917540672 | 14.75262202 |
| Full house | 8 | 0.34957575 | 2.796605997 |
| Four of a kind | 80 | 1.154502665 | 92.36021322 |
| Total | 12 | 116.5095989 |
EV of bonus with AAxxy = 116.5562273
EV of bonus with AAxxx = 116.6479072
Blended average of AA bonuses = 116.5185234
In conventional 8-5 Bonus, I show, on average, all hands with two aces on the deal have an EV of 1.856810.
I know I'm skipping a lot of steps, but here is the final table showing the value of the feature:
| Deal | Probability | Feature win | VP win | Add win | Value |
|---|---|---|---|---|---|
| two aces | 0.039930 | 116.518523 | 9.284049 | 107.234474 | 4.281853 |
| Three aces | 0.001736 | 291.276848 | 33.361938 | 257.914910 | 0.447761 |
| Total | 0.041666 | 4.729614 |
The bottom right cell shows the feature, in 8-5 Bonus, is worth 4.73 credits. However, the player must pay 5 credits for it. That gives the additional bet a return of 94.6%. I doubt it is that low. It should be greater than the 99.17% return of 8-5 Bonus.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
January 8th, 2020 at 5:19:09 AM
permalink
Quote: Wizard
If the player gets AAxyz (two aces and three singletons), here is the value of the subsequent 12-hand bonus.
Hand Pays Expected Win High pair 1 4.556604125 4.556604125 Two pair 2 1.021776788 2.043553576 Three of a kind 3 4.917540672 14.75262202 Full house 8 0.34957575 2.796605997 Four of a kind 80 1.154502665 92.36021322 Total 12 116.5095989
EV of bonus with AAxxy = 116.5562273
EV of bonus with AAxxx = 116.6479072
Blended average of AA bonuses = 116.5185234
I can confirm all the numbers in the section above. Bottom line, I also calculate that the blended average of AA bonuses = 116.5185234.
Quote: WizardThe bottom right cell shows the feature, in 8-5 Bonus, is worth 4.73 credits. However, the player must pay 5 credits for it. That gives the additional bet a return of 94.6%. I doubt it is that low. It should be greater than the 99.17% return of 8-5 Bonus.
I'm unclear as to why you think that this feature should improve the return to player. Think of the additional 5 credits that you pay for this feature as akin to a side-bet in a carnival game. A return of 94.6% then seems to be reasonable.
So many better men, a few of them friends, are dead. And a thousand thousand slimy things live on, and so do I.
January 8th, 2020 at 6:20:52 AM
permalink
Quote: gordonm888I'm unclear as to why you think that this feature should improve the return to player. Think of the additional 5 credits that you pay for this feature as akin to a side-bet in a carnival game. A return of 94.6% then seems to be reasonable.
Thank you for the confirmation.
The reason I am skeptical of the bottom line is Action Gaming video poker variants almost without fail make the return higher if the player bets more to pay for the feature.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
January 8th, 2020 at 6:24:22 AM
permalink
If I may, here is my math if the player is dealt three aces and two singletons.
Here is the summary. The bottom right cell shows the value of the bonus is 292.02 credits.
Can I get an amen?
| Hand | Three of a kind | Full house | Four aces |
|---|---|---|---|
| 1 | 0.896392 | 0.061055 | 0.042553 |
| 2 | 0.858248 | 0.058457 | 0.083296 |
| 3 | 0.821727 | 0.055969 | 0.122304 |
| 4 | 0.786760 | 0.053587 | 0.159653 |
| 5 | 0.753280 | 0.051307 | 0.195413 |
| 6 | 0.721226 | 0.049124 | 0.229650 |
| 7 | 0.690536 | 0.047033 | 0.262431 |
| 8 | 0.661151 | 0.045032 | 0.293817 |
| 9 | 0.633017 | 0.043116 | 0.323867 |
| 10 | 0.606080 | 0.041281 | 0.352639 |
| 11 | 0.580289 | 0.039524 | 0.380186 |
| 12 | 0.580289 | 0.039524 | 0.380186 |
| 13 | 0.555596 | 0.037842 | 0.406561 |
| Total | 9.144591 | 0.622851 | 3.232557 |
Here is the summary. The bottom right cell shows the value of the bonus is 292.02 credits.
| Hand | Pays | Expected | Win |
|---|---|---|---|
| Three of a kind | 3 | 9.144591 | 27.433774 |
| Full house | 8 | 0.622851 | 4.982811 |
| Four of a kind | 80 | 3.232557 | 258.604573 |
| Total | 13.000000 | 291.021158 |
Can I get an amen?
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
January 8th, 2020 at 9:42:47 AM
permalink
Quote: WizardIf I may, here is my math if the player is dealt three aces and two singletons.
Hand Three of a kind Full house Four aces 1 0.896392 0.061055 0.042553 2 0.858248 0.058457 0.083296 3 0.821727 0.055969 0.122304 4 0.786760 0.053587 0.159653 5 0.753280 0.051307 0.195413 6 0.721226 0.049124 0.229650 7 0.690536 0.047033 0.262431 8 0.661151 0.045032 0.293817 9 0.633017 0.043116 0.323867 10 0.606080 0.041281 0.352639 11 0.580289 0.039524 0.380186 12 0.580289 0.039524 0.380186 13 0.555596 0.037842 0.406561 Total 9.144591 0.622851 3.232557
Here is the summary. The bottom right cell shows the value of the bonus is 292.02 credits.
Hand Pays Expected Win Three of a kind 3 9.144591 27.433774 Full house 8 0.622851 4.982811 Four of a kind 80 3.232557 258.604573 Total 13.000000 291.021158
Can I get an amen?
You have modeled a stack of 13! Not a stack of 12!
For a stack of 12, I get AAA-xy = 258.549196 and AAA-xx = 258.6817704
I calculate that the blended average for AAA = 258.595987.
Unfortunately, the player return on this feature is slightly lower, if my values are correct.
So many better men, a few of them friends, are dead. And a thousand thousand slimy things live on, and so do I.
January 8th, 2020 at 11:18:44 AM
permalink
Quote: WizardIf I may, here is my math if the player is dealt three aces and two singletons.
Hand Three of a kind Full house Four aces 1 0.896392 0.061055 0.042553 2 0.858248 0.058457 0.083296 3 0.821727 0.055969 0.122304 4 0.786760 0.053587 0.159653 5 0.753280 0.051307 0.195413 6 0.721226 0.049124 0.229650 7 0.690536 0.047033 0.262431 8 0.661151 0.045032 0.293817 9 0.633017 0.043116 0.323867 10 0.606080 0.041281 0.352639 11 0.580289 0.039524 0.380186 12 0.580289 0.039524 0.380186 13 0.555596 0.037842 0.406561 Total 9.144591 0.622851 3.232557
Here is the summary. The bottom right cell shows the value of the bonus is 292.02 credits.
Hand Pays Expected Win Three of a kind 3 9.144591 27.433774 Full house 8 0.622851 4.982811 Four of a kind 80 3.232557 258.604573 Total 13.000000 291.021158
Can I get an amen?
I see now that the rules you have posted indicate a stack size of 13 for an AAA hand. So, please ignore my previous response. However, I note that your table above appears to have an error - hands 11 and 12 have identical entries. The totals for AAA-xy should be:
Trips: 9.096255856
Full House: 0.619559222
Quads: 3.284184922
I now calculate that the average value of the bonus for AAA hands = 295.0297323.
So many better men, a few of them friends, are dead. And a thousand thousand slimy things live on, and so do I.
January 8th, 2020 at 12:32:44 PM
permalink
Quote: gordonm888However, I note that your table above appears to have an error - hands 11 and 12 have identical entries.
Thank you! I had a feeling it was something stupid like that.
Quote:The totals for AAA-xy should be:
Trips: 9.096255856
Full House: 0.619559222
Quads: 3.284184922
I agree.
Quote:I now calculate that the average value of the bonus for AAA hands = 295.0297323.
That's what I get for AAAxx hands.
| Hand | Pays | Expected | Win |
|---|---|---|---|
| Three of a kind | 3 | 9.086869 | 27.260606 |
| Full house | 8 | 0.628946 | 5.031572 |
| Four of a kind | 80 | 3.284185 | 262.734794 |
| Total | 13.000000 | 295.026971 |
For a blended average of all three-ace hands, I get the following:
| 3K | Combinations | Probability | Avg win | Exp win |
|---|---|---|---|---|
| aaaxy | 4224 | 0.936170 | 294.980035 | 276.1515222 |
| aaaxx | 288 | 0.063830 | 295.026971 | 18.83150881 |
| Total | 4512 | 1.000000 | 294.983031 |
Thanks again Gordon!
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
January 8th, 2020 at 12:39:05 PM
permalink
Here are my bottom line results:
Given that it costs 10 credits per line, it makes the return 96.94%. That makes me feel a little better, but I still say it's unusual for Action Gaming to punish a player for betting more for the feature, but it has happened.
| Deal | Probability | Avg win | Return |
|---|---|---|---|
| Two aces | 0.039930 | 116.518523 | 4.652563 |
| Three aces | 0.001736 | 294.983031 | 0.512114 |
| Other | 0.958334 | 4.726608 | 4.529669 |
| Total | 9.694347 |
Given that it costs 10 credits per line, it makes the return 96.94%. That makes me feel a little better, but I still say it's unusual for Action Gaming to punish a player for betting more for the feature, but it has happened.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
January 8th, 2020 at 1:57:58 PM
permalink
Quote: Wizard
The reason I am skeptical of the bottom line is Action Gaming video poker variants almost without fail make the return higher if the player bets more to pay for the feature.
I believe it is a Nevada Gaming requirement that increasing the bet can not reduce the payback percentage of the machine.
At my age, a "Life In Prison" sentence is not much of a deterrent.
January 8th, 2020 at 6:49:26 PM
permalink
Quote: DRichI believe it is a Nevada Gaming requirement that increasing the bet can not reduce the payback percentage of the machine.
That is what happens in every side bet involving a capped envy bonus.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
January 8th, 2020 at 8:55:21 PM
permalink
I just updated my Stack 'em High page with details on my analysis of 8-5 Bonus Poker. I welcome all comments and especially corrections.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
January 8th, 2020 at 9:57:34 PM
permalink
Quote: WizardThat is what happens in every side bet involving a capped envy bonus.
I think there is something in the regs specific to video poker though.
January 8th, 2020 at 11:01:08 PM
permalink
Quote: WizardI just updated my Stack 'em High page with details on my analysis of 8-5 Bonus Poker. I welcome all comments and especially corrections.
Not for Stack 'em High but for the recent Dogs 3D entry (not presented at WOV), in Rule #1 replace the word "horses" with "dogs".
Have you tried 22 tonight? I said 22.
January 9th, 2020 at 1:39:18 AM
permalink
Quote: rsactuaryI think there is something in the regs specific to video poker though.
Not to doubt you, but I'd like to see a reg number.
In other news, I notice some of these games up the pay per coin when going from 4 to 5 coins in hands other than the royal. Here is deuces, for example.
Also note how the pay table in the game screen does not match the rule screen.
I suspect there is supposed to be a pay table change with a max coin bet that is not correctly shown for Bonus Poker at VideoPoker.com, which is causing my max bet return to go down.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
January 9th, 2020 at 2:12:58 AM
permalink
Quote: WizardNot to doubt you, but I'd like to see a reg number.
In other news, I notice some of these games up the pay per coin when going from 4 to 5 coins in hands other than the royal. Here is deuces, for example.
Also note how the pay table in the game screen does not match the rule screen.
I suspect there is supposed to be a pay table change with a max coin bet that is not correctly shown for Bonus Poker at VideoPoker.com, which is causing my max bet return to go down.
I'm not aware of the regulation forcing that an additional bet MUST up the return on a machine.
And yes, I wouldn't be shocked there is a paytable boost that is missing. IGT keeps making games with paytable boosts in recent years. It really tilts me. Because higher flushes mean tougher strategy!
January 9th, 2020 at 3:21:28 PM
permalink
Quote: tringlomaneAnd yes, I wouldn't be shocked there is a paytable boost that is missing. IGT keeps making games with paytable boosts in recent years. It really tilts me. Because higher flushes mean tougher strategy!
Thanks for your comments.
I see the deuces pay table is 1-2-2-3-5-9-12-20 for less than max bet, which has a return of 98.93%.
For max bets, the pay table is -1-2-3-4-4-14-16-20 for a return of 101.13%.
I am about 98.93% sure they forgot the pay table boost with some games, including Bonus Poker.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
January 9th, 2020 at 4:56:02 PM
permalink
Wizard, et al.,
Just a general procedure question.... How do you account for hands that cannot be made due to discarding? For example, if you are dealt:
Ah 2h 3s 5c 6c
Then discard the 2,3, 5 and 6, what impact do the hands that now cannot be made because of the discards have on the potential return (i.e., you now cannot make some straights, 4-of-a-kinds, 4-of-a-kinds with kicker, and straight flushes; and some others are now less likely since there are only three live ranks instead of four)? Is this lost potential accounted for somehow in the calculation of the Return?
Just a general procedure question.... How do you account for hands that cannot be made due to discarding? For example, if you are dealt:
Ah 2h 3s 5c 6c
Then discard the 2,3, 5 and 6, what impact do the hands that now cannot be made because of the discards have on the potential return (i.e., you now cannot make some straights, 4-of-a-kinds, 4-of-a-kinds with kicker, and straight flushes; and some others are now less likely since there are only three live ranks instead of four)? Is this lost potential accounted for somehow in the calculation of the Return?
Simplicity is the ultimate sophistication - Leonardo da Vinci
January 9th, 2020 at 5:37:52 PM
permalink
Quote: AyecarumbaWizard, et al.,
Just a general procedure question.... How do you account for hands that cannot be made due to discarding? For example, if you are dealt:
Ah 2h 3s 5c 6c
Then discard the 2,3, 5 and 6, what impact do the hands that now cannot be made because of the discards have on the potential return (i.e., you now cannot make some straights, 4-of-a-kinds, 4-of-a-kinds with kicker, and straight flushes; and some others are now less likely since there are only three live ranks instead of four)? Is this lost potential accounted for somehow in the calculation of the Return?
Yes, of course the discards, or penalty cards, are considered. The way my standard video poker program works is to cycle through all ways the 47 cards left in the deck can come out, average all the wins for all 32 ways to play a hand, and go with the choice that has the highest average win.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
January 17th, 2020 at 7:56:37 PM
permalink
I finally heard back from the math guy at VideoPoker.com. I was right that the game there incorrectly did not give the player the pay table boost for invoking the feature. In what is normally 8-5 Bonus Poker for 1-5 coins bet per hand, it bumps up to 10-7 with the feature.
Incorporating that rule, I get a return of 0.994248, which agrees with their number.
I just updated my Stack 'em High page with the 10-7 pay table and embellished the page with more details. Please have a look. As always, I welcome all comments. I worked hard on that page, so please have a look.
Incorporating that rule, I get a return of 0.994248, which agrees with their number.
I just updated my Stack 'em High page with the 10-7 pay table and embellished the page with more details. Please have a look. As always, I welcome all comments. I worked hard on that page, so please have a look.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
January 17th, 2020 at 9:36:30 PM
permalink
Wow. I am impressed with Wizard's impressive instincts and persistence. Very well done to cut through such a thick fog!
Comments.
1. Nice write-up.
2. The WOO page text says, in the Analysis Section: "Following is my analysis of 5-play 8-5 Bonus Poker. As a reminder, the game awards 12 bonus hands for two dealt aces and 13 for three. When the player invokes the feature, there is a pay table boost from 8-5 to 10-5."
Should that last part say "from 8-5 to 10-7" ??
3. Also, in the analysis section you refer to the game you are analyzing as "8-5 Bonus Poker" in most places but you also call it 10-7 Bonus Poker towards the end of the Analysis Section. And in your first table titled "Stack 'em High -- 5 Play" the game is referred to as Bonus Poker with a 10-7 Paytable. I feel sorry for the hapless individual who clicks on this page and tries to figure out which of the games listed in that first table you are analyzing. My suggestion would be to call it the same name in both the first table and consistently through-out the Analysis Section write-up - probably 10-7 Bonus Poker. Or something.
Comments.
1. Nice write-up.
2. The WOO page text says, in the Analysis Section: "Following is my analysis of 5-play 8-5 Bonus Poker. As a reminder, the game awards 12 bonus hands for two dealt aces and 13 for three. When the player invokes the feature, there is a pay table boost from 8-5 to 10-5."
Should that last part say "from 8-5 to 10-7" ??
3. Also, in the analysis section you refer to the game you are analyzing as "8-5 Bonus Poker" in most places but you also call it 10-7 Bonus Poker towards the end of the Analysis Section. And in your first table titled "Stack 'em High -- 5 Play" the game is referred to as Bonus Poker with a 10-7 Paytable. I feel sorry for the hapless individual who clicks on this page and tries to figure out which of the games listed in that first table you are analyzing. My suggestion would be to call it the same name in both the first table and consistently through-out the Analysis Section write-up - probably 10-7 Bonus Poker. Or something.
So many better men, a few of them friends, are dead. And a thousand thousand slimy things live on, and so do I.
