$1 Single Line vs. Multiline Jacks or Better 9/6 - Bankroll Difference?

Ok, I did post this question in my other thread - but figured it might deserve its own thread.

Here's my question:

Does playing multi-lines on a $1 JOB 9/6 - increase the amount I would need in my bankroll to have the same risk of ruin when compared to a single line at the same denomination?

Example: according to the wizard on wizardofodds.com (https://wizardofodds.com/games/video-poker/appendix/1/):
the bankroll needed for a 2.5% risk of ruin on a $1 JOB 9/6 full pay ($5 per hand)
with 1% in cashback:
is 7256 units or $36,280

So if I was playing $1 JOB 9/6 triple play ($15 per hand) (1% cashback)- what is the bankroll required here to have the same 2.5% risk of ruin?

1. $36,280?
2. ($36,280 X 3) = $108,840?
3. Or somewhere in between ($36,280 - $108,840)?

2 major points here:

1. The $15 cost to the get dealt the starting hand
2. but, you are "running it" 3 times, to get 3 different results from your starting hand - (thereby decreasing variance).

Any help on this is appreciated.

The idea of multi-line variance was discussed in another recent VP thread. You could probably find your answers in that thread.

My thoughts are that each has their own RNG and thus you're simply playing 3 separate games at a time, which means you'd get to the long run 3x as fast and thus experience LESS variance.

It was shown though that the hands are slightly correlated because of the starting hand being the starting cards for all 3, so while this does indeed get you to the long run faster, it could make for a slightly bumpier ride (i.e. more variance). There was shown (in that thread) to be slightly more variance when playing multi-line... Though if you have a "proper" bankroll for single line, I would think you're about on track and should be "okay" to play multi-line. Don't take that wrong and think you should go play 100 play all day, but understand that there is slightly more variance due to co-variance with multi-line.

Quote: Romes

The idea of multi-line variance was discussed in another recent VP thread. You could probably find your answers in that thread.

My thoughts are that each has their own RNG and thus you're simply playing 3 separate games at a time, which means you'd get to the long run 3x as fast and thus experience LESS variance.

It was shown though that the hands are slightly correlated because of the starting hand being the starting cards for all 3, so while this does indeed get you to the long run faster, it could make for a slightly bumpier ride (i.e. more variance). There was shown (in that thread) to be slightly more variance when playing multi-line... Though if you have a "proper" bankroll for single line, I would think you're about on track and should be "okay" to play multi-line. Don't take that wrong and think you should go play 100 play all day, but understand that there is slightly more variance due to co-variance with multi-line.

Ah, ok, thanks for the feedback.

Do you happen to know the name of the other thread this topic was discussed?

Thanks.

I clicked Gambling. I clicked Video Poker... I saw "How much more variance is triple plan than single line?"

...it's like 5 threads down.

Quote: Romes

I clicked Gambling. I clicked Video Poker... I saw "How much more variance is triple plan than single line?"

...it's like 5 threads down.

Found it. I read through it. However, although the thread talks about how the triple play and multilines are more variance- it does not talk about bankroll. I understand the higher the variance - the larger your bankroll needs to be - but by how much ? Is what I am trying to figure out.

Your variance should go in to your Bankroll calculations. Use the variance you see for the game you want and figure out the long run...

After 1,000,000 hands your EV is X, plus or minus 3SD... EV - 3SD is a good number for bankroll as that should encompass (with 99.9% certainty) every likely outcome. i.e. You know, with 99.9% certainty, the worst you could do is EV - 3SD... So if your bankroll is that amount, you know - with 99.9% certainty - that you won't bust (RoR = 0).

I believe Bob Dancer and others have software that can calculate your bankroll for you given inputs.

getting to the long run does not reduce variance. I think there is this confusion again about the long run making results closer to expected value ... this happens by viewing it as a percentage, but does not happen in dollars. In fact, as Mathextremist recently pointed out, in dollars it gets less and less likely to be exactly the same as the EV [while closer as a percentage]

common sense would also seem to say you need a bigger bankroll

Getting to the long run reduces your standard deviations within respect of your EV. It's quite possible for many hours/hands or trials of any game to have your SD be greater than your EV for some time. The point is when you hit "the long run" of the game you're playing it is mathematically impossible for your SD to be greater than your EV at that point... (at least in the games we're discussing, such as VP). Thus, if you're playing with an advantage your advantage is realized because you're guaranteed to be positive.

I disagree with the last part though... If you want to play 1,000,000 hands of VP. You can calculate your 3SD for 1 hand, 100 hands, 10,000 hands, 100,000 hands and 1,000,000 hands. Your 3SD will be the largest at the largest number of trials. Largest as in physically the largest amount. Thus, what you're saying at 1,000,000 hands is I expect EV, plus or minus 3SD, where 3SD is (with 99.9% certainty) the mathematically WORST you can do.

If you encompass the worst case scenario in your bankroll, where all other points in the timeline must be smaller 3SD's, then you should reduce your RoR to zero.

Show Your Work

Let's assume you found a pay table in JoB which gave you a 1% advantage, thus the payback was 101%.

Variance = 19.514676, SD = 4.417542 (from the wiz)

AvgAdv = 1%
AvgBet = $5 ($1 single line, 5 coins)
OriginalSD = SD * AvgBet = 4.4 * 5 = 22

SD(x hands) = SQRT(x) * OriginalSD... Thus:

Num Hands	Expected Value	3 SD
1	$0.05	+-$66.00
1,000	$50.00	+-$2,087.10
10,000	$500.00	+-$6,600
100,000	$5,000	+-$20,871.03
1,000,000	$50,000	+-$66,000
5,00,000	$250,000	+-$147,580.49

Thus, we can see that "the long run", or N0, or "break even"... whatever you want to call it... is between 1,000,000 and 5,000,000 hands as with 3SD of confidence at 5,000,000 hands we will GUARANTEED mathematically have profits.

This tells us that if you have a bankroll of ~$150,000... your RoR (with 99% confidence) is 0. Actually, it'll be less than that. You need to find the exact break even point and take 3SD at that number of trials. I'll leave that as an exercise for the OP.

Quote: Romes

<snip>where 3SD is (with 99.9% certainty) the mathematically WORST you can do.

100% FALSE.
nice try
Oh,
yuk try, imo

to be outside of 3 sd is easy at a 1 in 371 chance
happens all the time
and more times when one says it can't happen

real money is lost and won gambling
only thing that matters

hajhahahaj
"the mathematically WORST you can do"
take that to the bank!
<<<>>>
for the OP
there are software that calculates bankrolls and risk of ruin for VP game sessions
one still has to understand what 1 in 20 can mean for example

most have no clue or think it means something totally from what it does mean.
have fun and have luck

Quote: mustangsally

100% FALSE.
nice try
Oh,
yuk try, imo...

Wikipedia disagrees with you.

...3σ = .1, thus comes with 99.9% confidence.

Quote: Romes

Wikipedia disagrees with you.

...3σ = .1, thus comes with 99.9% confidence.

no
no
you seemed challenged these days.
actually it is OK
<<<>>>
3σ
99.7300204%
see the outside that range
hehe
<<<>>>
it is OK
I just stand up for the truth
it is fun!

you due lots of math that is fun
and use advanced concepts to show things are this way and that way
but come to really poor conclusions at times...imo

but that is OK
I just called U on it

I say help out the OP for what is asked for then show feathers
right ME
I can do the same for funs

Quote: stabworld

Example: according to the wizard on wizardofodds.com (https://wizardofodds.com/games/video-poker/appendix/1/):
the bankroll needed for a 2.5% risk of ruin on a $1 JOB 9/6 full pay ($5 per hand)
with 1% in cashback:
is 7256 units or $36,280

link is not working for me
and to me that bankroll for 2.5% ror seems too high

in Video Poker for Winners it shows for a 2.5% ror
$1 JOB 9/6 full pay ($5 per hand) with 1% in cashback

29,060 bankroll is required.

I found VPWinners to be very accurate
but who knows at this point in time?
this can easily be simulated too

Quote: stabworld

So if I was playing $1 JOB 9/6 triple play ($15 per hand) (1% cashback)- what is the bankroll required here to have the same 2.5% risk of ruin?

1. $36,280?
2. ($36,280 X 3) = $108,840?
3. Or somewhere in between ($36,280 - $108,840)?

fun question
and many might offer their opinions too

VP for Winners shows 34,810

I find this interesting enough to look into it more, at a later date
of course
maybe on April 1

thanks for asking!
Sally

Where are we playing 9/6 with 1% cash back? Or is that accounting for mailers and all.

Quote: Romes

You need to find the exact break even point and take 3SD at that number of trials. I'll leave that as an exercise for the OP.

how did we get from the bankroll needed for multiple lines vs single lines, to all this?

you've established that using SDs that a figure for safe bankroll can be derived in a +EV game, that's interesting, nice job and something I can follow well, which is unusual, so thanks. I'd have to guess, however, that's re-inventing the wheel for a lot of folks, since Kelly and RoR calculations seem to be what's referred to most.

It is certainly true that the variance decreases with more, smaller betting as long as the total action is the same. That is in fact why Kelly is calculated for +EV and why the House likes small but numerous bets in -EV [for player]. However, I am pretty unconvinced this means you need a smaller bankroll for multi-line betting than single line betting because that business of total action I'd expect to increase with the former.

Quote: stabworld

<snip>
https://wizardofodds.com/games/video-poker/appendix/1/

the bankroll needed for a 2.5% risk of ruin on a $1 JOB 9/6 full pay ($5 per hand)
with 1% in cashback:
is 7256 units or $36,280

now I see what you did
1% RoR = 7256 units
2.5% RoR = 5812 units

the link you entered in the OP does not need these ( ) around it

so I feel good about the Video Poker for Winners results 4 3 play
I figure no need to do any more figuring unless you like figures

2.5% ruin
is high to me
(1 in 40. almost like American Roulette betting on that one number to WIN)
hate to lose that much when
1% RoR could get one to the promised land.

have funs!
Sally

Quote: odiousgambit

how did we get from the bankroll needed for multiple lines vs single lines, to all this?

April Fools!!

that's me

Quote: GWAE

Where are we playing 9/6 with 1% cash back? Or is that accounting for mailers and all.

It's accounting for: "Multiplier promo day". (mailers not included in the 1% cashback)

Quote: mustangsally

now I see what you did
1% RoR = 7256 units
2.5% RoR = 5812 units

(Yes - exactly)

Quote: mustangsally

link is not working for me
and to me that bankroll for 2.5% ror seems too high

in Video Poker for Winners it shows for a 2.5% ror
$1 JOB 9/6 full pay ($5 per hand) with 1% in cashback

29,060 bankroll is required.



VP for Winners shows 34,810


Sally

Sally - thanks for your input. If you don't mind me asking - I have VP for Winners also - can you tell me exactly how you derived at the above bankroll amounts?

do you click on:
-analyze
-bankroll?

from that point I'm lost - I have no idea what to input into the following fields:

-standard deviation?
-win frequency?
-variance?

Quote: stabworld

from that point I'm lost - I have no idea what to input into the following fields:

-standard deviation?
-win frequency?
-variance?

input nothing there
those values are computed for u already
click the lower right Risk of Ruin button

now enter your values
leave the one blank that you want
and click the button you want
like so


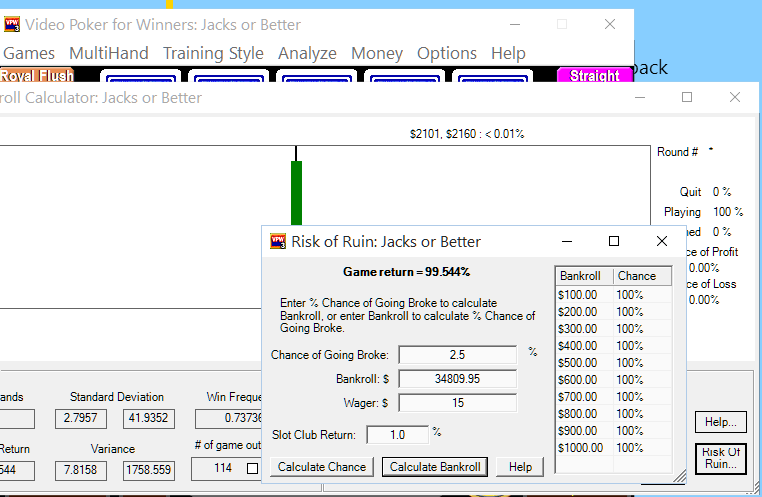
it works for me
and matches another program I have too
Sally

Quote: mustangsally

input nothing there
those values are computed for u already
click the lower right Risk of Ruin button

now enter your values
leave the one blank that you want
and click the button you want
like so


it works for me
and matches another program I have too
Sally

Sally - When I enter $15 as the wager - 1% as the slot club return - and 2.5% risk of ruin - its giving me $87,178.32 as a required bankroll.

=144950449&filters[recent]=1&sort=1&o=0]

Cant seem to quite get the image to appear on my post.

Here is the URL link to the picture:

http://s1378.photobucket.com/user/stabworld/media/Untitled_zpsv5tpwfoy.jpg.html?filters[user]=144950449&filters[recent]=1&sort=1&o=0

Quote: stabworld

Sally - When I enter $15 as the wager - 1% as the slot club return - and 2.5% risk of ruin - its giving me $87,178.32 as a required bankroll.

i never have to enter how much the bet is
it is already filled in for me

looks like you did JOB 9/6
single play
for $15

and

I did JOB 3-play for $15
maybe
place $5 for the bet and that should match what the Wizard had

The way I look at it, without big wins, you're going to see less starting hands. Less starting hands would be less opportunities to see three and four to a royal where you'll usually connect. If you don't see four to a royal, you probably won't get one. If you get the good starting hands, multihand you'll connect, but have to get to where you see them first. The one thing about multi is mistakes are multiplied all at once and that's going to hurt you. Same concept as playing a slot one line versus five, if you lose 100 bets, 100 coins will get you even, but five line, you need a rarer hit for more money to bust the slump.