Poll
 | 2 votes (16.66%) | ||
 | 4 votes (33.33%) | ||
 | 2 votes (16.66%) | ||
| No votes (0%) | |||
| No votes (0%) | |||
| No votes (0%) | |||
| No votes (0%) | |||
| No votes (0%) | |||
| No votes (0%) | |||
 | 4 votes (33.33%) |
12 members have voted
March 15th, 2016 at 8:34:25 PM
permalink
Super Draw 6 Card Poker is a new video poker variant I noticed at VideoPoker.com. The idea is simple -- the player gets a sixth card on the draw. Of course, nothing is ever free. The player must double his bet for this extra card. There are some new six-card hands added to the pay table too.
Example:
Here I'm dealt three deuces.
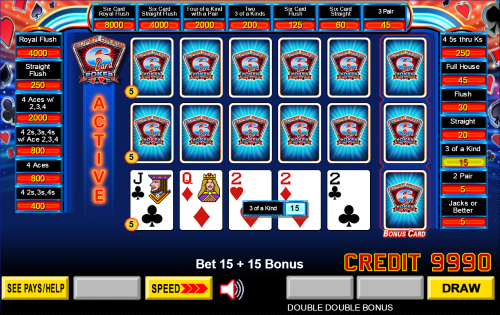
I hold the three deuces. Of the three hands, one improves to a full house and the other to a four of a kind.

So far I have only done a scoring function. Here is how often each hand occurs in Double Double Bonus, if the game dealt six cards on the deal, which it doesn't. Where two wins are possible, I go with the one that pays more. When two pays are still possible, for example with suited 9TJQKA, it is arbitrary which one I count it as.
That said, here is my score array:
The question for the poll is would you play Super Draw 6 Card Poker, given the same return as conventional video poker?
Example:
Here I'm dealt three deuces.

I hold the three deuces. Of the three hands, one improves to a full house and the other to a four of a kind.

So far I have only done a scoring function. Here is how often each hand occurs in Double Double Bonus, if the game dealt six cards on the deal, which it doesn't. Where two wins are possible, I go with the one that pays more. When two pays are still possible, for example with suited 9TJQKA, it is arbitrary which one I count it as.
That said, here is my score array:
| Hand | Pays | Count |
|---|---|---|
| Six-card royal flush | 1600 | 4 |
| Six-card straight flush | 800 | 32 |
| Royal flush | 800 | 114 |
| Four of a kind + pair | 400 | 936 |
| Four aces + 2-4 | 400 | 480 |
| Four 2-4 + A-4 | 160 | 1,440 |
| Four aces + 5-K | 160 | 576 |
| Four 2-4 + 5-K | 80 | 1,728 |
| Straight flush | 50 | 930 |
| Four 5-K + 5-K | 50 | 9,504 |
| Two three of a kind | 40 | 1,248 |
| Six-card flush | 25 | 6,828 |
| Six-card straight | 12 | 36,828 |
| Three pair | 9 | 61,776 |
| Full house | 9 | 164,736 |
| Five-card flush | 6 | 199,080 |
| Five-card straight | 4 | 325,440 |
| Three of a kind | 3 | 732,160 |
| Two pair | 1 | 2,471,040 |
| Jacks or better | 1 | 3,000,756 |
| Nothing | 0 | 13,342,884 |
| Total | 20,358,520 |
The question for the poll is would you play Super Draw 6 Card Poker, given the same return as conventional video poker?
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
March 15th, 2016 at 8:48:01 PM
permalink
I have and would play this game, though I like several others better (QQ's, HotRoll, SplitPoker to name 3).
I also don't get why anybody likes Rent. But I had to choose only 1 answer.
I also don't get why anybody likes Rent. But I had to choose only 1 answer.
If the House lost every hand, they wouldn't deal the game.
March 15th, 2016 at 9:07:05 PM
permalink
Went to go try it, but seems that it's the only game in the free list that says you have to be gold.
DUHHIIIIIIIII HEARD THAT!
March 16th, 2016 at 1:19:20 AM
permalink
Something is wrong with your scoring array. Royal flush should be 4 suits * 46 cards that don't make a 6 card Royal.
Others are also off, but I can't check them until I get home.
Others are also off, but I can't check them until I get home.
“Man Babes” #AxelFabulous
March 16th, 2016 at 7:36:27 AM
permalink
Quote: mipletSomething is wrong with your scoring array. Royal flush should be 4 suits * 46 cards that don't make a 6 card Royal.
Others are also off, but I can't check them until I get home.
Good catch. I'm working on fixing that.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
March 16th, 2016 at 10:44:03 AM
permalink
Okay, here is my new and improved hand count array.
I previously had some problems scoring hands that could be both straights and flushes, but not necessarily the same cards in each of them.
| Hand | Pays | Count |
|---|---|---|
| Six-card royal flush | 1600 | 4 |
| Six-card straight flush | 800 | 28 |
| Royal flush | 800 | 184 |
| Four of a kind + pair | 400 | 936 |
| Four aces + 2-4 | 400 | 480 |
| Four 2-4 + A-4 | 160 | 1,440 |
| Four aces + 5-K | 160 | 576 |
| Four 2-4 + 5-K | 80 | 1,728 |
| Straight flush | 50 | 1,444 |
| Four 5-K + 5-K | 50 | 9,504 |
| Two three of a kind | 40 | 1,248 |
| Six-card flush | 25 | 6,608 |
| Six-card straight | 12 | 36,624 |
| Three pair | 9 | 61,776 |
| Full house | 9 | 164,736 |
| Five-card flush | 6 | 198,924 |
| Five-card straight | 4 | 325,440 |
| Three of a kind | 3 | 732,160 |
| Two pair | 1 | 2,471,040 |
| Jacks or better | 1 | 3,000,756 |
| Nothing | 0 | 13,342,884 |
| Total | 20,358,520 |
I previously had some problems scoring hands that could be both straights and flushes, but not necessarily the same cards in each of them.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
March 16th, 2016 at 11:27:10 AM
permalink
Here is what I have so far:
we disagree on 2 of them:
Six-card straight flush: 4 suits * 8 6-card straights (A-6 through 8-K) = 32
Straight flush: 4 suits * 8 5-card straights (2-6 throuh 9-k) * 45 cards that don't make a 6-card straight flush. +
4 suits * 1 (A-5 straight) * 46 cards that don't make a 6-card straight flush
4*8*45+4*1*46=1624
| Hand | Ways |
|---|---|
| Six-card royal flush | 4 |
| Six-card straight flush | 32 |
| Royal flush | 184 |
| Four of a kind + pair | 936 |
| Four aces + 2-4 | 480 |
| Four 2-4 + A-4 | 1440 |
| Four aces + 5-K | 576 |
| Four 2-4 + 5-K | 1728 |
| Straight flush | 1624 |
| Four 5-K | 9504 |
| Two three of a kind | 1248 |
| Six-card flush | |
| Six-card straight | |
| Three pair | 61776 |
| Full house | 164736 |
| Five-card flush | |
| Five-card straight | |
| Three of a kind | 732160 |
| Two pair | |
| Jacks or better | |
| Nothing |
we disagree on 2 of them:
Six-card straight flush: 4 suits * 8 6-card straights (A-6 through 8-K) = 32
Straight flush: 4 suits * 8 5-card straights (2-6 throuh 9-k) * 45 cards that don't make a 6-card straight flush. +
4 suits * 1 (A-5 straight) * 46 cards that don't make a 6-card straight flush
4*8*45+4*1*46=1624
“Man Babes” #AxelFabulous
March 16th, 2016 at 12:21:32 PM
permalink
Here is version 3:
Looks like we agree on what you have so far.
| Hand | Pays | Count |
|---|---|---|
| Six-card royal flush | 1600 | 4 |
| Six-card straight flush | 800 | 32 |
| Five-card Royal flush | 800 | 184 |
| Four of a kind + pair | 400 | 936 |
| Four aces + 2-4 | 400 | 480 |
| Four 2-4 + A-4 | 160 | 1,440 |
| Four aces + 5-K | 160 | 576 |
| Four 2-4 + 5-K | 80 | 1,728 |
| Five-card straight flush | 50 | 1,624 |
| Four 5-K + 5-K | 50 | 9,504 |
| Two three of a kind | 40 | 1,248 |
| Six-card flush | 25 | 6,580 |
| Six-card straight | 12 | 36,612 |
| Three pair | 9 | 61,776 |
| Full house | 9 | 164,736 |
| Five-card flush | 6 | 198,780 |
| Five-card straight | 4 | 325,440 |
| Three of a kind | 3 | 732,160 |
| Two pair | 1 | 2,471,040 |
| Jacks or better | 1 | 3,000,756 |
| Nothing | 0 | 13,342,884 |
| Total | 20,358,520 |
Looks like we agree on what you have so far.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
March 16th, 2016 at 3:59:41 PM
permalink
I have my program up and running for this game. It takes 12.3 hours to work through a pay table so I won't know until tomorrow morning how it's working.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
March 17th, 2016 at 4:53:44 PM
permalink
I think my program is working properly. Here are the results for 9-6 Double Double Bonus, which is available at VideoPoker.com. The return column is the product of the win, probability, and 0.5 (because the player must double his bet to pay for the feature). So, 99.32% return.
VideoPoker.com link
| Hand | Pays | Combinations | Probability | Return |
|---|---|---|---|---|
| Six-card royal flush | 1600 | 376,189,752 | 0.000003 | 0.002157 |
| Six-card straight flush | 800 | 2,286,403,812 | 0.000016 | 0.006554 |
| Four of a kind + pair | 400 | 53,862,873,696 | 0.000386 | 0.077205 |
| Two three of a kind | 40 | 65,862,044,532 | 0.000472 | 0.009440 |
| Six-card flush | 25 | 438,221,653,116 | 0.003141 | 0.039258 |
| Six-card straight | 12 | 566,514,956,100 | 0.004060 | 0.024361 |
| Three pair | 9 | 1,081,046,587,176 | 0.007748 | 0.034864 |
| Five-card Royal flush | 800 | 10,081,123,716 | 0.000072 | 0.028900 |
| Five-card straight flush | 50 | 60,590,252,904 | 0.000434 | 0.010856 |
| Four aces + 2-4 | 400 | 21,304,708,188 | 0.000153 | 0.030537 |
| Four 2-4 + A-4 | 160 | 55,526,542,512 | 0.000398 | 0.031836 |
| Four aces + 5-K | 160 | 24,144,767,196 | 0.000173 | 0.013843 |
| Four 2-4 + 5-K | 80 | 63,303,595,992 | 0.000454 | 0.018147 |
| Four 5-K + 5-K | 50 | 354,234,143,508 | 0.002539 | 0.063468 |
| Full house | 9 | 4,159,440,047,808 | 0.029810 | 0.134144 |
| Five-card flush | 6 | 5,523,829,609,812 | 0.039588 | 0.118764 |
| Five-card straight | 4 | 3,764,795,765,184 | 0.026981 | 0.053963 |
| Three of a kind | 3 | 11,278,297,316,688 | 0.080829 | 0.121244 |
| Two pair | 1 | 27,093,903,864,696 | 0.194176 | 0.097088 |
| Jacks or better | 1 | 21,377,316,797,196 | 0.153207 | 0.076603 |
| Nothing | 0 | 63,537,674,376,816 | 0.455361 | 0.000000 |
| Total | 139,532,613,620,400 | 1.000000 | 0.993233 |
VideoPoker.com link
Last edited by: Wizard on Mar 17, 2016
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
March 18th, 2016 at 10:37:16 AM
permalink
Here is my score frequency for Bonus Deuces. I welcome all confirmations and/or corrections. When two or more wins are possible, I go with the one that pays the most.
| Hand | Count | Pays |
|---|---|---|
| Six-card royal flush | 4 | 1,600 |
| Four deuces + pair | 72 | 800 |
| Six of a kind | 264 | 200 |
| Six-card wild royal flush | 760 | 50 |
| Six-card straight flush | 2,816 | 20 |
| Six-card flush | 17,100 | 9 |
| Six-card straight | 392,748 | 5 |
| Five-card natural royal | 184 | 800 |
| Four deuces + ace | 176 | 400 |
| Four deuces | 880 | 200 |
| Five-card wild royal flush | 19,968 | 25 |
| Five aces | 2,288 | 80 |
| Five 3-5 | 6,864 | 40 |
| Five 6-K | 17,536 | 20 |
| Five-card straight flush | 79,640 | 13 |
| Four of a kind | 599,472 | 4 |
| Full house | 507,936 | 3 |
| Five-card flush | 472,776 | 3 |
| Five-card straight | 1,031,856 | 1 |
| Three of a kind | 3,697,440 | 1 |
| Nothing | 13,507,740 | - |
| Total | 20,358,520 |
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
March 24th, 2016 at 7:01:28 AM
permalink
I'm proud to say that my new page on Super Draw 6 Poker is ready for preview. I'm still working on adding more return tables to it. I'm cranking through a couple more as I write this (each takes up to 15 hours to loop through).
Please click on the link and have a look. As always, I welcome all questions, comments, and especially corrections.
Please click on the link and have a look. As always, I welcome all questions, comments, and especially corrections.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
March 24th, 2016 at 10:34:52 AM
permalink
Just added a return table for 9-7 Triple Double Bonus.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
September 10th, 2016 at 2:36:17 AM
permalink
I'm playing this game for the first time. If I'm dealt a quad where the kicker card doesn't matter (for example, 8,8,8,7), am I better off holding that fifth card so now I only need to match that card on the 6-card draw (ie. draw another 7) for the quad+pair payout, or should I toss the fifth card and hope to draw a pair, or does it not make a difference at all?
March 13th, 2023 at 11:48:24 PM
permalink
To answer this question, it is actually mathematically equivalent to throw away the fifth card, or hold it. Essentially, for draw purposes, it is irrelevant when the fifth card comes in the cycle, either on the deal or the draw. The only thing you can make is a pair, so the sequence of operations doesn't matter.


