How to calculate odds of a particular return (or worse) for a session?

I had a session the other day that was pretty bad and I had a 91.5% return over 6000 hands on 8/5 BP. I know this is certainly a rare occurrence based on lots of prior results, but what is the formula to come up with how often a session will be that bad? Thanks!

Quote: abacabb

I had a session the other day that was pretty bad and I had a 91.5% return over 6000 hands on 8/5 BP.

and you would not call that ugly bad?

Quote: abacabb

I know this is certainly a rare occurrence based on lots of prior results,

oh oh
how rare?

does not seem that rare to me,
but i could be wrong without looking

Quote: abacabb

but what is the formula to come up with how often a session will be that bad? Thanks!

THE formula for only 6000 hands played.
i know there are vp programs to figure this out

but
THE formula

like X = Y/2
for vp ?
JUNEbe
Don has one he wants to share

calling Don

It's probably easier to run a simulation, Video Poker for Winners has a feature that will allow you to run exactly this sort of simulation.

For Bonus Poker you could probably get away with dividing the sessions in 2 scenarios, those that you hit a royal and those that you didn't and then run normal approximation for all the small pays.

Relevant Information for BP:

Cycle Length of Royal 40,233
Overall Game Return 99.16%
Overall Variance 20.91
Return of game excluding royals 97.17%
Variance of game excluding royals 5.02


To determine the probability of each scenario you can use the exponential distribution, I assume you didn't hit a royal.

Probability of 0 Royals=exp(-6000/40,233) ~ 86%

Z score of non-royal scenario= (.915-.9717)/sqrt(5.02*6000)*6000=-1.96

The probability of getting a Z-score of -1.96 or lower is about 2.5%

Overall approximation = 2.5%*86% ~2%

Overall I get a probability of about 2% but I made a lot of assumptions, you'd probably get a more accurate number from just running the sim.

Quote: Tortoise

Overall I get a probability of about 2% but I made a lot of assumptions, you'd probably get a more accurate number from just running the sim.

Assuming we were using the same pay table, I ran 500,000 sets of 6000 hands, and got a 91.5% or worse return about 1/59 of the time.

Quote: ThatDonGuy

Assuming we were using the same pay table, I ran 500,000 sets of 6000 hands, and got a 91.5% or worse return about 1/59 of the time.

i would have thought you would have tried to calculate it

it is easy for a program to do, i mean computers do compute when given the chance

and for
losing 510 units or more that calculated probability i get = 1.687473% or abouts 1 in 59.26

and
the probability of being down 510 or more units within 6,000 hands (not just at the end) is almost 2 * 1.687473%
wow

not even rare by my standards as i thought


must love variance
love
love
love

but to some, this could be rare on a small sample

===============================
some other values for entertainment (the program does this without asking)
-600 units
0.331111% or abouts 1 in 302.01
-650: 0.112443, 889.3394876
-700:0.033334, 2,999.940001
-800:0.001884, 53,078.55626
-900: 0.000056, 1,785,714.286

Thank you Don
Sally

Quote: mustangsally

i would have thought you would have tried to calculate it

Actually, I did try, but statistics isn't my strongest card in the deck - and how do you apply normal distribution to something with a mean of about 1 and a standard deviation > 4? I don't think there's a 16% chance of the return being -3 or less; that would require the machine to actually extend a vacuum hose of some sort and suck up three times what you bet from your pockets.

There's also no exact way of calculating the value of the integral used for cumulative normal distribution; you have to approximate it using, e.g., Simpson's Rule.

Thanks for the replies. I figured there would be some easy mathematical formula that I was just unaware of, but I wound up writing a simulation as well. As both of you are coming up with 1/59 it seems like mine is wrong in some spot -- I will take a look at it later, but I wound up getting 0.6002% chance of a final result worse than being -510 units in 6000 hands and 0.9506% chance of losing at least 510 units in 6000 hands.

Quote: abacabb

Thanks for the replies. I figured there would be some easy mathematical formula that I was just unaware of, but I wound up writing a simulation as well. As both of you are coming up with 1/59 it seems like mine is wrong in some spot -- I will take a look at it later, but I wound up getting 0.6002% chance of a final result worse than being -510 units in 6000 hands and 0.9506% chance of losing at least 510 units in 6000 hands.

What (probability, value) pairs are you using?
I used:
Royal flush: (0.000025, 800)
Straight flush: (0.000107, 50)
4 aces: (0.000196, 80)
4 2-4: (0.000527, 40)
4 5-K: (0.001640, 25)
Full house: (0.011514, 8)
Flush: (0.010880, 5)
Straight: (0.011221, 4)
3 of a kind: (0.074468, 3)
Two pair: (0.129308, 2)
Jacks/better: (0.215259, 1)
Nothing: (0.544855, 0)
Then ran 6000 hands and counted how many had a total return of (6000 x 0.915) = 5490 or lower.
You can also subtract 1 from each of those value numbers (i.e. Royal Flush is 799; Jacks or Better is 0; Nothing is -1) and see how many times your total is -510 or lower.

Quote: abacabb

I wound up getting 0.6002% chance of a final result worse than being -510 units in 6000 hands and 0.9506% chance of losing at least 510 units in 6000 hands.

How are these two events different? Does the second one include when you are -510 or lower at some point but finish above -510?


Okay, time for another round of Teach That Don Guy Another Statistics Lesson...
I ran 2.1 million sets of 6000 hands using the above numbers (the total returns ranged from 5013 to 9935), and got:
Mean 5949.521227 (99.1587% return)
The return was 5490 (91.5%) or worse in 1 / 59.62171471 of the sets
However, I get a SD of 353.5085642, which means the Z Score for 5940 is only -1.3 instead of the expected -2.1225 or so.
SD = square root of variance = square root of (sum of (probability of a particular result x (result - mean)²) over all possible results), isn't it?

Then again, graphing the results does show that they do form three peaks - a large one at around 5800, a smaller one at around 6625, and a really small but definitely noticeable one at around 7425, so that would skew any "normal" SD calculations, especially for values less than the mean.

I found the error, I had the flush value set to 6 instead of 5. Now I get numbers that agree. 1.6678% chance of having a final result of -510 or worse and a 2.4998% chance of having a loss of -510 or more at some point. Yes, the second number includes those trials where you are at -510 but wind up finishing above that amount.

I'd be happy to share my code if anyone is interested. It's written in C and takes a paytable with probabilities in a plain text file as an input, so it will work with any arbitrary game.

Quote: abacabb

I found the error, I had the flush value set to 6 instead of 5. Now I get numbers that agree. 1.6678% chance of having a final result of -510 or worse and a 2.4998% chance of having a loss of -510 or more at some point. Yes, the second number includes those trials where you are at -510 but wind up finishing above that amount.

Ah, i see i posted the wrong info for that
i guess i was in a hurry and wanted to say about 1% higher than the end value

here is the sim i ran
2.57% bust rate up to 6k hands played


and

Quote: abacabb

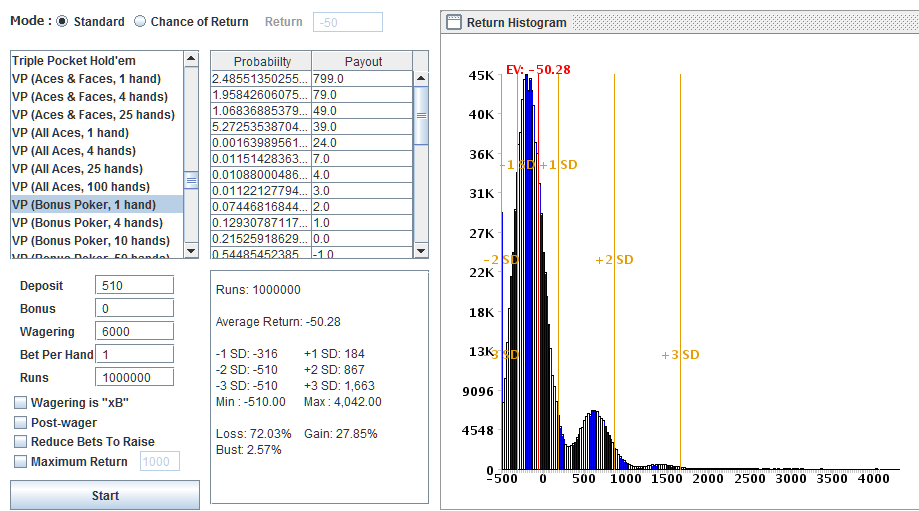
I'd be happy to share my code if anyone is interested.

being happy is a good thing
i mean
would you be sad to share your code?

thank you for sharing

i MAY get my vp convolve code working for this (i use it for dice and smaller, closer paytables)

i use a program to compute the values and it uses a Markov chain (as i also use in Excel)
of course it can take a minute or longer to compute as the chain gets larger and larger but it does cut off at 1 in a billion probabilities
so i happy about that
Sally

here is a short video of the program
i can do a better video when i have more time

Here's my code. Compile with your favorite C compiler.

http://pastebin.com/WqGGhGJ0

Then create a file for the payout schedule.

http://pastebin.com/jLcfsBpC

Assuming you call your file schedule, then invoke the program as follows

As an example, the below run produces the output below

8276 trials out of 500000 worse than a final result of of -510 (1.655200%)
12491 trials out of 500000 worse than a loss of -510 (2.498200%)