When the Progressive Reaches +EV Levels for Players

I’ve found the Wizard’s video poker calculators helpful, and I know he provides a mathematical analysis on Three Card Poker.

I was curious if anyone knows how I can calculate when the $1 progressive bet on a Three Card Poker table provides the player +EV when factoring in the element of risk of making only a $5 wager ($5 ante bet or $5 ante + $5 play bet).

TIA

I will add that the Progressive usually starts at $1,000. I’m also happy to provide payables for both the game and the progressive.

Quote: HotBlonde

I will add that the Progressive usually starts at $1,000. I’m also happy to provide payables for both the game and the progressive.
link to original post

That will likely be necessary.
It can be hard to do math without numbers.

Are you talking about AKQ spades for the progressive? Lot of variations for progressive. I have seen people play 6 card bet and almost never hit anything.

Quote: avianrandy

Are you talking about AKQ spades for the progressive? Lot of variations for progressive. I have seen people play 6 card bet and almost never hit anything.
link to original post

Quote: Dieter

That will likely be necessary.
It can be hard to do math without numbers.
link to original post

To be clear, I’m looking to calculate with only the $1 PROGRESSIVE bet being the ONLY bonus bet I make on top of the $5 Ante/Play bet(s). No Pair Plus included or 6-Card Bonus.

Information:

I play perfect strategy of Q64 or higher each hand

Ante Bonus Pays-
Straight Flush 5 to 1
Three of a Kind 4 to 1
Straight 1 to 1

Progressive-
Royal Flush (spades only) 100% of PROGRESSIVE amount ($1,000 +)
Royal Flush Spades Envy $100
Royal Flush (hearts, diamonds or clubs) 500 for 1
Royal Flush Other Suits Envy $25
Straight Flush 70 for 1
Three of a Kind 60 for 1
Straight 6 for 1

*For those who may not know, the envy is paid out to you if another player on the table makes a royal, not you.

As a super big cherry on top, if anyone can show me their formula (you can DM it to me if you’d like), I’d love to see how the math was done. Either way, I am looking for the answer to my original question in the first part of this post above.

According to a site I found on the internet,if the meter starts at 5k the house edge is 70%. For each 1k over the 5k, the player gains 4.5% at 10k their is no house edge.at $11,500 and up is when it becomes favorable. Likelihood of AKQ spades is every 22,100 hands. Hope this helps

Quote: HotBlonde

Quote: avianrandy

Are you talking about AKQ spades for the progressive? Lot of variations for progressive. I have seen people play 6 card bet and almost never hit anything.
link to original post

Quote: Dieter

That will likely be necessary.
It can be hard to do math without numbers.
link to original post

To be clear, I’m looking to calculate with only the $1 PROGRESSIVE bet being the ONLY bonus bet I make on top of the $5 Ante/Play bet(s). No Pair Plus included or 6-Card Bonus.

Information:

I play perfect strategy of Q64 or higher each hand

Ante Bonus Pays-
Straight Flush 5 to 1
Three of a Kind 4 to 1
Straight 1 to 1

Progressive-
Royal Flush (spades only) 100% of PROGRESSIVE amount ($1,000 +)
Royal Flush Spades Envy $100
Royal Flush (hearts, diamonds or clubs) 500 for 1
Royal Flush Other Suits Envy $25
Straight Flush 70 for 1
Three of a Kind 60 for 1
Straight 6 for 1

*For those who may not know, the envy is paid out to you if another player on the table makes a royal, not you.

As a super big cherry on top, if anyone can show me their formula (you can DM it to me if you’d like), I’d love to see how the math was done. Either way, I am looking for the answer to my original question in the first part of this post above.
link to original post

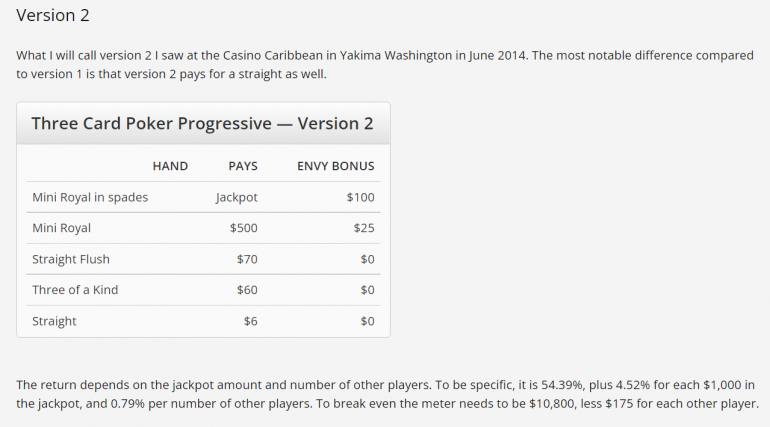
According to the Wizard's Three Card Poker page, the house edge for your ante bet is 3.3730%.

To overcome the 3.3730% house edge on your $5 ante bet and also the $1 spent making the side bet, the $1 progressive bet has to have a return of (3.3730%)($5) + $1 = $1.16865 or 116.865%.

Refer to the picture below to find how big the progressive has to be. Let's ignore the envy bonuses for now. The Wizard says that the return is 54.39% plus 4.52% for each $1000 of progressive. So, all we have to do is solve this equation for P, which is the progressive prize:

116.865% = 54.39% + ( P / 1000 )(4.52%)

The answer is approximately P = $13,822.

To account for the envy bonuses, subtract $175 from P for each other player, as advised by the Wizard below.

Quote: ChesterDog

According to the Wizard's Three Card Poker page, the house edge for your ante bet is 3.3730%.

To overcome the 3.3730% house edge on your $5 ante bet and also the $1 spent making the side bet, the $1 progressive bet has to have a return of (3.3730%)($5) + $1 = $1.16865 or 116.865%.

Refer to the picture below to find how big the progressive has to be. Let's ignore the envy bonuses for now. The Wizard says that the return is 54.39% plus 4.52% for each $1000 of progressive. So, all we have to do is solve this equation for P, which is the progressive prize:

116.865% = 54.39% + ( P / 1000 )(4.52%)

The answer is approximately P = $13,822.

To account for the envy bonuses, subtract $175 from P for each other player, as advised by the Wizard below.


link to original post

BEAUTIFUL, ChesterDog! Just the answer I was looking for. Much appreciated. And thank you too, avianrandy. 💜

Awww you're a sweetheart. Chester dog was very much more spot on. I wish you much fool luck and that akq spades in your future. I have had 2 of those cards in my hand,but the king was off suit but still a straight nonetheless. Glad I was able to help somewhat. We are all here to help each other

*good luck. Gotta love autocorrect lol